基于能量粒子算法的无线自组织网络节点移动策略研究*

刘半藤

(浙江树人大学信息工程学院,杭州 310015)

无线自组织网络MANETs(Mobile Ad Hoc Networks)是由若干可以自由移动节点组成的高度自治系统。由于部署MANETs无需依靠已有的通信设备,具有较强的抗毁性与适用性,被广泛地应用于抗震救灾、野外探测等各种环境,被视为21世纪信息技术的重要产业支柱之一[1]。受限的节点能量与动态变化的拓扑结构是MANETs区别于传统网络的重要特征。由于MANETs节点大多分布于野外环境中,需要依靠电池供电且长时间内无法充电。网络能耗已经成为限制MANETs发展的重要因素,也成为国内外专家学者研究的热点领域[2]。节点的移动使得网络拓扑结构实时变化,网络能量优化计算变得更为困难。因此,研究一种节点移动策略改善网络能耗状况是一项非常有意义的工作。

目前,MANETs节点移动策略对于网络性能的影响主要表现在以下几个方面[3-10]:时间同步问题、网络连通性问题、网络能耗问题、网络覆盖率问题。王慧强等人[3]针对水下传感器网络移动性对时间同步参数计算带来的困难,提出一种通信量小、精度高的时间同步算法。刘宴涛等人[4]分别建立随机点移动策略、随机方向移动策略、随机游走移动策略分析MANETs连通性状况,证明随机游走移动策略使得网络具有较高连通性。与此同时,王珊珊等人[5]改进传统的随机游走移动策略,并在仿真平台NS3实现一种以圆形为边界的随机游走移动模型,以提高网络连通性。吴聪等人[6]在经典随机点移动策略基础上,建立能量均衡的线性规划数学模型,说明节点移动性有助于提升MANETs能耗均衡性。无独有偶,Pala等人[7]利用节点移动特性,建立线性规划模型对无线传感网络的能量均衡指标进行优化。王珊等人[8]建立节点移动模型,提出一种修复网络覆盖空洞的联合补丁法,从而实现降低网络节点冗余度和提高网络覆盖率的目的。Wang等人[9]针对无线传感网络覆盖问题,指出在网络中部署少量移动节点有助于提高网络覆盖性能,并在三种典型应用场景进行仿真分析。Liu等人[10]从二维平面入手,考虑一般凸三维曲面的覆盖率,并以此作为传感器节点移动特征参数,及时填补覆盖空洞。在上述几方面中,节点移动对于网络覆盖性与能耗均衡两方面的研究更加重要。如何通过节点移动性,提升网络整体覆盖性以及改善能耗指标是衡量移动策略的重要指标。由于网络节点移动性使得网络能耗优化模型计算变得更为复杂。目前,MANETs节点移动策略主要有以下几种方式:虚拟力算法VFA(Virtual Force Algorithm)、粒子群算法PSO(Particle Swarm Optimization)。李明等人[11]结合传统虚拟力算法和差分算法,提出一种异构无线传感网络的节点移动策略,提升网络覆盖性能,且计算效率较高。李娟等人[12]以路由算法为基础,建立包含障碍物模型、速度初始化函数、无边界仿真区域的粒子群算法,并进行数值仿真以此说明算法的有效性。传统的粒子群算法在计算迭代过程中每个粒子都要实时获得全局最优的粒子位置,利用全局最优位置和局部最优位置信息指导粒子移动。这一点在MANET节点移动过程中较难实现。如果MANETs节点实时获知网络所有粒子的位置,需要进行集中式控制,所花费代价也较大。因此,较多传统的粒子群算法较难直接应用于MANETs。

为此,本文提出一种基于能量粒子的节点移动策略EPSO(Energy Particle Swarm Optimization)。EPSO将网络中的节点类比为粒子,每个节点都可以获得本地节点能量的局部最优信息和邻居节点的局部最优信息。通过将邻居节点的局部最优信息看作全局较优解,从而制定策略指导节点进行移动,提升网络能耗性能。

1 粒子模型

1.1 网络连通率计算方法

由N个移动节点构成的MANET可视为N个粒子散布在网络中(下文将网络中的节点称为粒子),并对粒子进行标号为i=1,2,…,N。在时刻t,标号为i的粒子位置可以表示为向量Pi(t)={pxi(t),pyi(t)}。每个粒子都具备相同的通信半径Rcom和感知半径Rcov。粒子可以与通信半径内的其他粒子进行信息交互。在时刻t,MANET连通矩阵C(t)=(cij(t))N×N的计算方式如下所示:

如果cij(t)=1,说明该时刻两个粒子间的距离小于通信半径。此时,该两个粒子可以直接进行信息交互。由于MANET的多跳传输特性,在连通矩阵C(t)的基础上,经过多跳传输后粒子间连通状况矩阵MC(t)=[mcij(t)]N×N的计算方式如下所示:

如果mcij(t)=1,说明该时刻两个粒子可以通过多跳传输进行信息交互。在时刻t,网络连通率指标L(t)的计算方式如下所示:

该指标衡量可以统计某时刻可以实现两两信息交互的粒子对总数所占网络粒子对总数的百分比。一种较好的移动策略可以有效保障粒子之间的连通特性。

1.2 网络覆盖率计算方法

将原有的MANET进行网格化划分,离散成M个独立的特征点,并对这些特征点进行标号为i=1,2,…,M。标号为i的特征点位置可以表示为向量Pti(t)={xi(t),yi(t)}。在时刻t,粒子对于特征点的覆盖状况矩阵G(t)=[gij(t)]N×M的计算方式如下所示:

如果gij(t)=1,说明该时刻标号为i的粒子可以感知标号为j的特征点。对于某个特征点而言,若存在一个粒子可以感知该特征点则可认为该特征点被覆盖。定义网络粒子i的冗余度yi(t)为该节点感知范围内的特征点被覆盖的平均粒子数,计算方式如下:

对于某个特征点而言,若存在一个粒子可以感知该特征点则可认为该特征点被覆盖。在时刻t,特征点被覆盖的状况矩阵TG(t)=[tgj(t)]1×M的计算方式如下所示:

利用特征点被感知的数量占特征点总数近似计算网络覆盖率F(t)计算方式如下:

1.3 网络能耗计算方法

假设MANET粒子能量消耗方式服从一阶能耗模型[13],结构如图1所示。

图1 一阶能量消耗模型

粒子发送数据包消耗能量包括发射电路耗能、放大电路耗能两部分,粒子接收数据只有接收电路消耗能量,计算方式如下:

式中:ETx表示发送能量消耗,ERx表示接收能量消耗,Eelec表示发射电路和接收电路的能耗,l表示发送数据包的比特数,d表示发送粒子与目的粒子之间的传输距离,εfs是模型常数。

2 能量粒子移动策略

2.1 粒子能量维全局较优解与局部最优解计算方法

图2 粒子能量维局部最优解与全局较优解搜索图

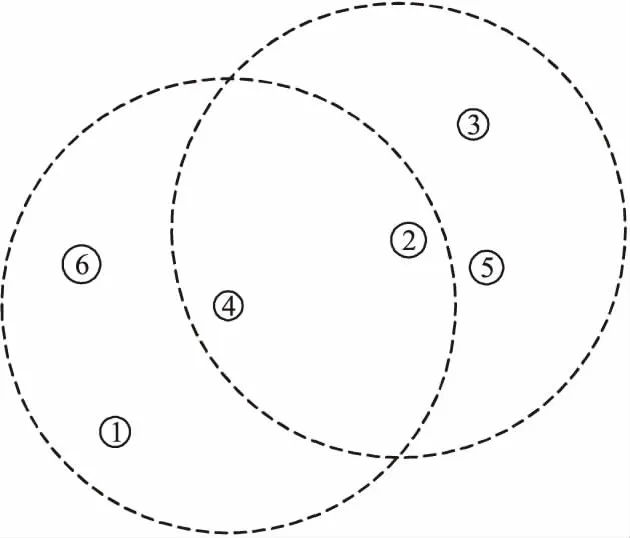
图3 粒子能量信息搜索举例

由于MANET网络多跳传输特性,粒子将承担转发任务。因此,粒子将努力向剩余能量较高的邻居粒子移动,从而降低剩余能量较低的粒子作为中间粒子转发信息的概率,实现提高网络生存时间的目的。

2.2 粒子覆盖维全局较优解与局部最优解计算方法

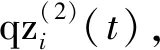
图4 粒子覆盖维局部最优解与全局较优解搜索图

2.3 粒子移动策略

通过上式可以发现:t时刻第i个节点根据自身的位置坐标Pi(t)确定需要改变的移动速度fi(t+Δt),从而确定下一时刻的节点位置Pi(t+Δt)。其中,c1与c2被称为学习因子或者加速度常数;r1与r2是属于[0,1]范围内服从均匀分布的随机数;ω被称为惯性权重。

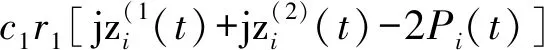
这就是本文提出的能量粒子移动策略EPSO,改善传统PSO算法所要求的全局最优粒子位置无法获得的困境。本文仅考虑从能量角度对经典的PSO算法进行改进,如果要考虑多个因素时也可构建多维PSO算法求解节点移动多目标优化解。因此,本文的算法具有较好的扩展性。

3 仿真分析

为了验证该能量粒子移动策略的性能,本节采用MATLAB2018b构建一个300 m×300 m矩形MANET仿真环境。初始时刻,网络中随机散布着50个移动节点,每个节点的覆盖半径为50 m,通信半径为60 m。节点进行业务传输时首先选择剩余能量较高的节点作为中间节点转发信息。

假设网络初始时刻每个节点的初始能量为10 J。设移动策略参数为c1=c2=2,ω=1。对比仅用局部最优信息的粒子群移动策略(PSO)和传统的虚拟力移动策略(VFA),三种移动策略下网络覆盖率指标变化曲线如图5所示,三种移动策略下网络连通率指标变化曲线如图6所示。

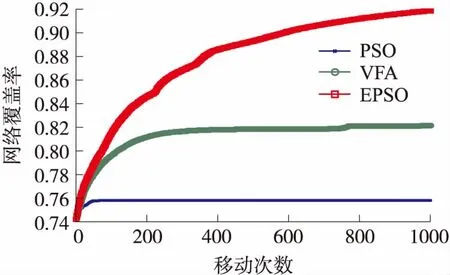
图5 三种策略下网络覆盖率指标变化趋势图

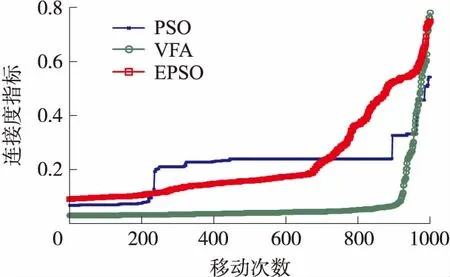
图6 三种策略下网络连通率指标变化趋势图

通过图5、图6可以发现:网络节点的移动特性可以有效地提高网络覆盖率指标,且本文提出的EPSO策略覆盖率高于仅用局部最优信息的PSO策略和传统的虚拟力移动策略(VFA)。但是,三种移动策略均使得网络连通性指标提交较为缓慢。这是由于在移动过程中对于连通度指标考虑不足所造成。

定义MANET中剩余能量最低的节点为瓶颈节点。三种移动策略下网络瓶颈节点能量变化曲线如图7所示,三种移动策略下网络剩余节点数量如图8所示。

图7 三种策略网络瓶颈节点能量变化趋势图

图8 三种策略网络生存节点数变化趋势图

通过图7、图8可以发现:EPSO移动策略下,网络的瓶颈节点随时间发生着变化,且瓶颈节点的能量随时间下降的速度较仅考虑局部信息的粒子群算法移动策略与传统虚拟力移动策略更为缓慢,可以延长网络生存时间。

4 结束语

本文在分析网络节点能量消耗模型的基础上,借鉴粒子群的移动方式,提出了一种能量粒子群算法的无线自组织网络节点移动策略。EPSO将网络中的节点类比为粒子,每个节点都可以获得本地节点能量的局部最优信息和邻居节点的局部最优信息。通过将邻居节点的局部最优信息看作全局较优解,从而制定策略指导节点进行移动,提升网络能耗性能。