商用车电瓶箱支架振动疲劳试验方法对比分析

贺娜，王党青，田朋涛，樊梅梅

（1.陕西重型汽车有限公司，陕西 西安710200；2.陕西汉德车桥有限公司，陕西 西安 710200）

关键字：商用车；电瓶箱支架；振动疲劳试验；道路模拟试验；正弦扫频试验 中图分类号：U467

引言

众所周知，零部件中80%以上的失效问题是由于振动疲劳引起。随着汽车工业的快速发展，结构设计中的疲劳耐久问题越来越受到大家的重视，在新车型开发过程中，考核地面振动对零部件耐久性能影响是最重要的试验项目之一。

考虑到整车搭载试验费用高、周期不可控，通过台架试验对零部件振动耐久性能进行验证成为主要试验手段。目前，台架振动耐久主要采取两种方式：一种是利用单自由度振动台对零部件的振动耐久性能进行验证；一种是利用道路模拟试验技术对零部件的振动耐久性能进行验证[1]。对于一些非标设计的支架类，没有专门的台架试验规范和标准，如何确定一种快速、经济、有效的支架振动试验验证方法来考核其薄弱环节，保证支架结构强度和疲劳寿命满足使用要求十分必要[2]。

本文通过对道路模拟试验方法和正弦扫频振动试验方法的介绍，并将两种试验方法应用于电瓶箱支架振动疲劳试验，通过对比分析，确定该类支架的振动试验方法，为企业如何根据自身实际需要建立一套该类支架的台架试验规范提供依据，为新产品研发提供技术支持。

1 试验方法介绍

1.1 道路模拟试验方法[3-4]

道路模拟试验指把整车及其零部件本身作为一个振动系统，通过对其振动传递特性及实际采集响应信号的测试计算，得到在试验室条件下的系统激励，经过数据反复迭代计算，保证整车及零部件的响应与道路试验条件下的响应达到一定的精度要求。对于室内台架道路模拟试验而言，核心是时域波形复现技术（TWR），它的本质是一个非线性系统的迭代求逆问题，主要包括系统识别和目标迭代两个部分。

1.1.1 系统识别

系统识别是通过一个位移u(t)为输入，以试验典型参考位置的响应信号y(t)为输出的多输入多输出MIMO 系统的数学模型，通常是以系统的频响函数FRF 矩阵形式表征线性模型。

图1 系统识别示意图

（1）激励信号：一般选择编制白粉噪声作为随机激励信号，计算公式为：

式中：fst、fen分别为起始频率和截止频率，fb为拐角频率。

（2）频响函数获取：

将时域激励信号u(t)和响应信号y(t)进行傅里叶变换，采用H1 技术来获取系统的频响函数矩阵，计算公式为：

式中，U(f)、Y(f)分别是随机信号u(t)、y(t)的傅里叶变换，U*(f)、Y*(f)分别是U (f)、Y (f)共轭，Gxx(f)、Gxy(f)分别是u(t)、y(t)的自功率谱和互功率谱。

（3）FRF 模型验证：

一般通过相干函数来评价FRF 的质量，相干函数计算公式为：

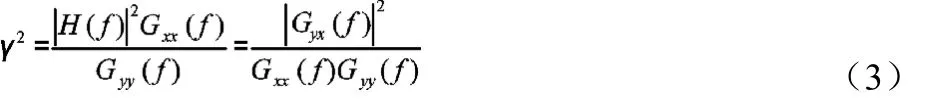
1.1.2 目标信号迭代

（1）初始驱动信号：由试验目标信号和识别出的FRF逆矩阵反算，求得初始驱动信号，计算公式为：

式中，F 是傅里叶变换；dg 分别是驱动系数和目标系数，T(f)是频域目标信号，u(t)是初始位移驱动信号。

（2）Error 计算：由初始驱动信号驱动振动系统获得输出响应信号，将该信号与试验获得的目标信号对比，计算误差Error，计算公式为：

式中，T(t)是时域目标信号，y(t)是系统响应，e(f)是频域误差。

（3）最终驱动信号确定：通过Error 来修正驱动信号，直至误差Error 达到试验要求，获得最后的驱动信号，计算公式为：

式中，i 是迭代次数；k 是误差系数。

1.2 正弦扫频试验方法[5-7]

正弦扫频试验是指在规定的频率范围内，按规定的量值以一定的扫描速率从低频到高频，再由高频到低频进行频率扫描来激励试验件，直到达到规定的试验次数为止。这里介绍的主要是以样件的低阶共振频率为中心频率的正弦扫频试验方法。

1.2.1 固有频率

结构系统在受到外界瞬态激励产生响应时，将按特定频率发生自然振动，这个特定频率被称为结构的固有频率。固有频率是结构的固有属性，与外界的激励无关。对于单自由度系统而言，固有频率的计算公式见下式：

式中：k 为系统的刚度；m 为系统的质量。

当外界激励与系统的固有频率非常接近或相同时，结构出现大幅度振动，该频率称为共振频率，该现象被称为共振现象。

1.2.2 功率谱密度PSD

功率谱及功率谱密度是从能量的角度来进行信号的频域分析。功率谱除以其频率间隔定义为功率谱密度。功率谱函数通常是对周期函数进行分析时使用的，而非周期函数和随机函数只能使用功率谱密度，功率谱和功率谱密度计算公式见下式：

功率谱：

功率谱密度：

1.2.3 对数扫频

对数扫频是指在对数频率刻度上，频率均匀变化的频率-时间关系，计算公式见下式：

扫频频率：

扫频时间：

扫频总次数：

式中f1、 f2为扫频试验频率下、上限。

2 电瓶箱支架振动耐久试验

2.1 电瓶箱支架道路模拟试验

电瓶箱支架是将整个电瓶箱体以及电池系统固定于车架上的过渡支架。在试验过程中，将其与整个电瓶箱体及电池系统作为一个整体来进行验证。在某试验场进行道路载荷谱采集的过程中，将响应传感器布置于电瓶箱体附件上。该处采集到的道路载荷谱详见图2 所示。

图2 载荷谱数据

道路载荷谱数据采集完成后将其进行编辑和处理，加载到六自由度试验台上，通过系统识别和迭代确定最终驱动信号，并将其加载到试验台上进行振动疲劳试验。

2.2 正弦扫频振动试验

通过对在试验场采集到的道路载荷谱进行PSD 分析，见下图3 所示。从PSD 图上可看到振动能量主要集中在Z 向，故选择在电磁振动台上进行Z 向的振动耐久试验，将样件安装于电磁振动试验台上，响应加速度传感器布置位置与试验场载荷谱采集位置保持一致。响应加速度选取Z 向载荷谱最大加速度值7.265g，在5-50HZ 内扫频反推振动台体的控制加速度值，取一个接近的控制加速度值作为最终的控制加速度，利用共振原理，选取（15-18）HZ 作为扫频频带进行正弦扫频试验，扫频曲线详见图4 所示。

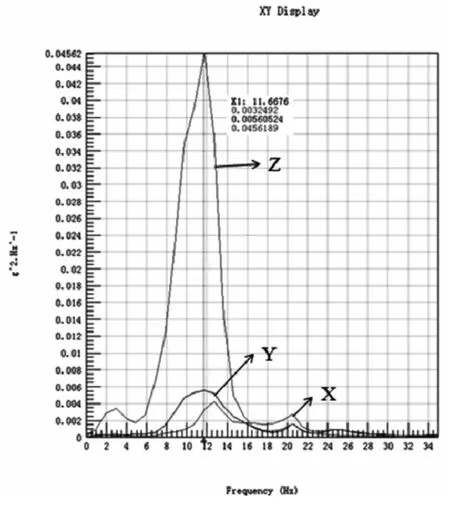
图3 载荷谱PSD 图

图4 扫频曲线

2.3 试验结果分析对比

应用以上两种试验方法完成试验后，将试验结果进行统计梳理：道路模拟试验电瓶箱支架有6 处开裂位置，正弦扫频振动试验电瓶箱支架有7 处开裂位置。

从支架开裂位置来看，通过两种试验方法得到的支架的开裂位置有5 处相同，故认为支架开裂位置基本一致。在支架开裂位置基本一致的前提下，通过对开裂位置发生时间进行统计可知，道路模拟试验电瓶箱支架的平均试验里程为1348km（试验时间按照路谱运行速度可换算为44.93h），正弦扫频振动试验电瓶箱支架的平均试验时间为3.41h。

根据该支架振动试验情况，对上面两种试验方法进行对比，详见下表1 所示。

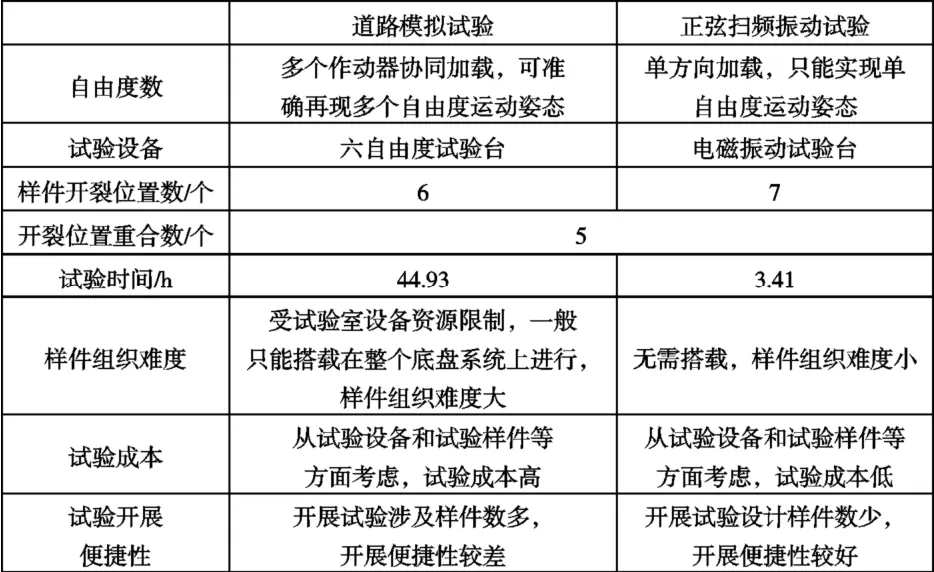
表1 电瓶箱支架振动试验方法对比

从上表可看出，对于电瓶箱支架而言， 从试验时间、试验成本和试验开展的便捷性等方面来考虑，推荐使用正弦扫频振动试验方法对该类支架薄弱环节进行考核。

3 结论

本文通过对道路模拟试验方法和正弦扫频振动试验方法的介绍，并将两种试验方法应用于电瓶箱支架振动疲劳试验。通过试验结果对比可知：

（1）从支架开裂位置来看，通过两种试验方法得到的支架的开裂位置有5 处相同，认为应用两种振动试验方法考核得到的开裂位置即薄弱环节基本一致。

（2）在支架开裂位置基本一致的前提下，道路模拟试验电瓶箱支架的平均试验时间为44.93h，正弦扫频振动试验电瓶箱支架的平均试验时间为3.41h，后者试验验证时间短。

（3）对于电瓶箱支架而言，从试验时间、试验成本等方面来考虑，推荐使用正弦扫频振动试验方法对该类支架薄弱环节进行考核。

本文得出的结论在一定程度上能够指导该类支架振动耐 久试验进行，为企业根据自身实际需要建立一套该类支架的台架试验规范提供依据，为新产品研发提供技术支持。但因素考虑有限，在后续的研究中应考虑疲劳损伤等因素，更加全面的对该类支架的振动耐久试验方法进行研究分析。