激光跟踪仪与室内GPS的协同测量组网方法

(航空工业北京长城计量测试技术研究所，北京 100095)

大型装备制造过程逐步朝着数字化与智能化方向发展，数字化测量技术不仅成为产品设计、加工、制造、装配及检测等全生命周期内质量的检测手段，更成为制造过程状态监控的主要信息来源，为产品质量提高、制造周期缩短提供有效方法[1-3]。因此，大型装配制造过程中的测量任务往往具备大尺度、高精度、高效率、高稳定性等特点和需求，仅靠单一系统的测量手段难以满足[4-7]。以大部件对接任务为例，开始对接过程中要求对接部件位姿的实时监控测量，需要进行多点位高效率的实时监控，不需要太高精度；而在对接最终阶段需要对关键点位进行高精度测量，其数据为部件的下一步运动提供准确的参数，需要进行高精度的测量[8]。激光跟踪仪和室内GPS均是新型的数字化测量仪器的代表，若单采用激光跟踪仪在后期精度可得以保证，但难以完成对接过程的实时监控；若单采用室内GPS可实时监控对接过程，但对接精度则不足[9]。采用激光跟踪仪和室内GPS组成协同测量网络，在统一基准的前提下充分发挥两种系统的优势，是解决对接这类问题的有效手段[9]。这种利用多种设备协同测量完成同一测量任务的工作模式已成为国内外一大研究热点[10]。国外，波音公司利用激光跟踪仪与 V-STARS系统组成协同测量网络，其中激光跟踪仪用于进行关键控制点的测量，而V-STARS系统以密集点云的形式测量波音787飞机外翼的外形轮廓，为飞机外形装配准确度检测和逆向重构提供了数据基础[11]。在国内，解放军工程大学的范百兴教授研究了激光跟踪仪与经纬仪的组网方法，在现场获得了应用[12]；天津大学的邾继贵教授团队研究了多站位室内GPS的组网方法，达到了亚毫米的精度[13]。

测量精度是衡量测量网络性能的重要指标，高精度的组网方法是保证测量精度的有效手段[14]。本文在研究激光跟踪仪和室内GPS的数学模型基础上，根据两种系统的特点，采用了基于传感单元观测量的方法构建基本约束方程，为提高整体算法精度，在测量网络内引入了一维基准尺和三维控制场作为相对约束进行优化，采用了Levenberg-Marquardt 算法进行最优化求解，为保证迭代过程设计了基于后方交汇原理的迭代初值求解方法。最终通过实验验证了组网方法的精度优于±0.06 mm，可在工业现场推广应用。

1 测量原理

1.1 激光跟踪仪测量原理

激光跟踪仪是典型的球坐标系测量系统，通过两个高精度码盘观测点位相对于站位的水平角和垂直角，同时通过干涉测距模块观测点到站位距离，以极坐标计算的方式唯一确定测量点三维坐标。其测量过程中的坐标系示意图如图1所示。

根据水平角φ、垂直角θ和距离r可以唯一确定观测点P(x,y,z)，可由数学公式表示：

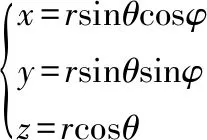
(1)

由任意跟踪仪坐标系下的测量点坐标P(x,y,z)也可反求水平角φ、垂直角θ和距离r，可由数学公式表示：

(2)

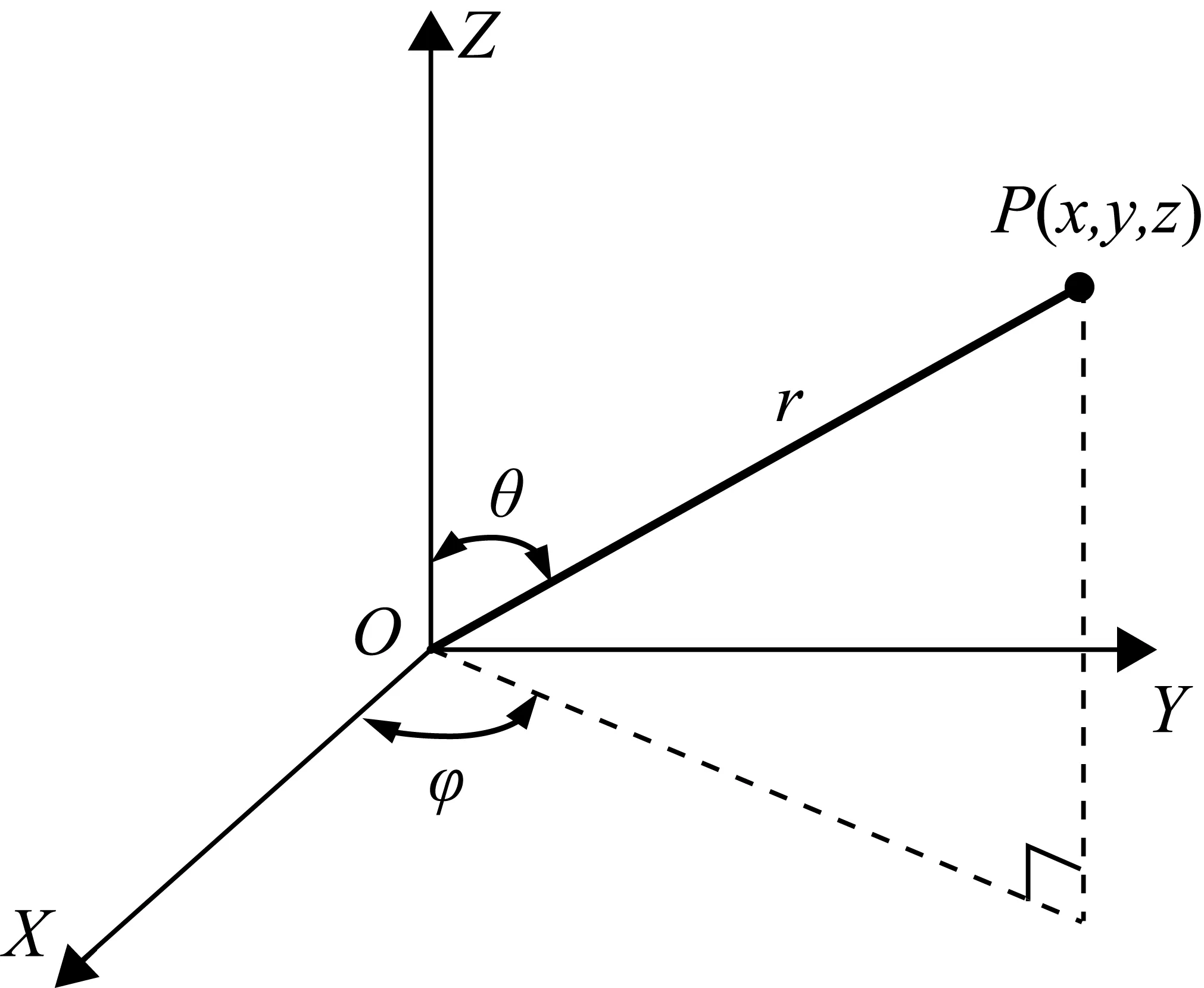
图1 激光跟踪仪测量过程中的坐标系示意图

1.2 室内GPS测量原理

室内GPS是一种基于光电扫描的多站位大尺寸坐标测量系统，系统组成如图2所示，主要包括：发射站、接收器、信号处理器和解算工作站。发射站发射两束绕着转轴匀速旋转并带有一定倾斜的激光扇面，在被测空间内实现扫描；接收器感应光信号，并转化为旋转角度；信号处理器和解算工作站之间通过无线传输模块进行通信，解算工作站对接收到的时间信息进行处理后进行坐标的解算、显示及存储，同时还负责管理整个系统资源，包括现场组网参数以及资源使用权限的分配等。

图2 室内GPS结构示意图

发射站的结构示意图和数学模型如图3所示。发射站主要由转子和基座组成，转子带动两个线性激光发射器高速绕转轴旋转，因此发射站可以抽象为绕着旋转轴旋转的两个非平行激光扇面，激光扇面与旋转轴间具有一定的倾角，其结构参数即两激光扇面在发射站坐标系下的方程作为一项重要参数在发射站安装完成后通过标定精确给定。发射站的数学模型如下：首先，建立发射站坐标系OXYZ，定义旋转轴为Z轴，激光扇面1和旋转轴的交点为原点O，激光扇面1上过原点且与旋转轴垂直的直线为X轴，根据右手定则确定Y轴。发射站逆时针旋转，发射站两激光扇面的平面方程为

(3)

式中,(a1,b1,c1,d1)T，(a2,b2,c2,d2)T为预先标定好的光平面1及光平面2的结构参数。

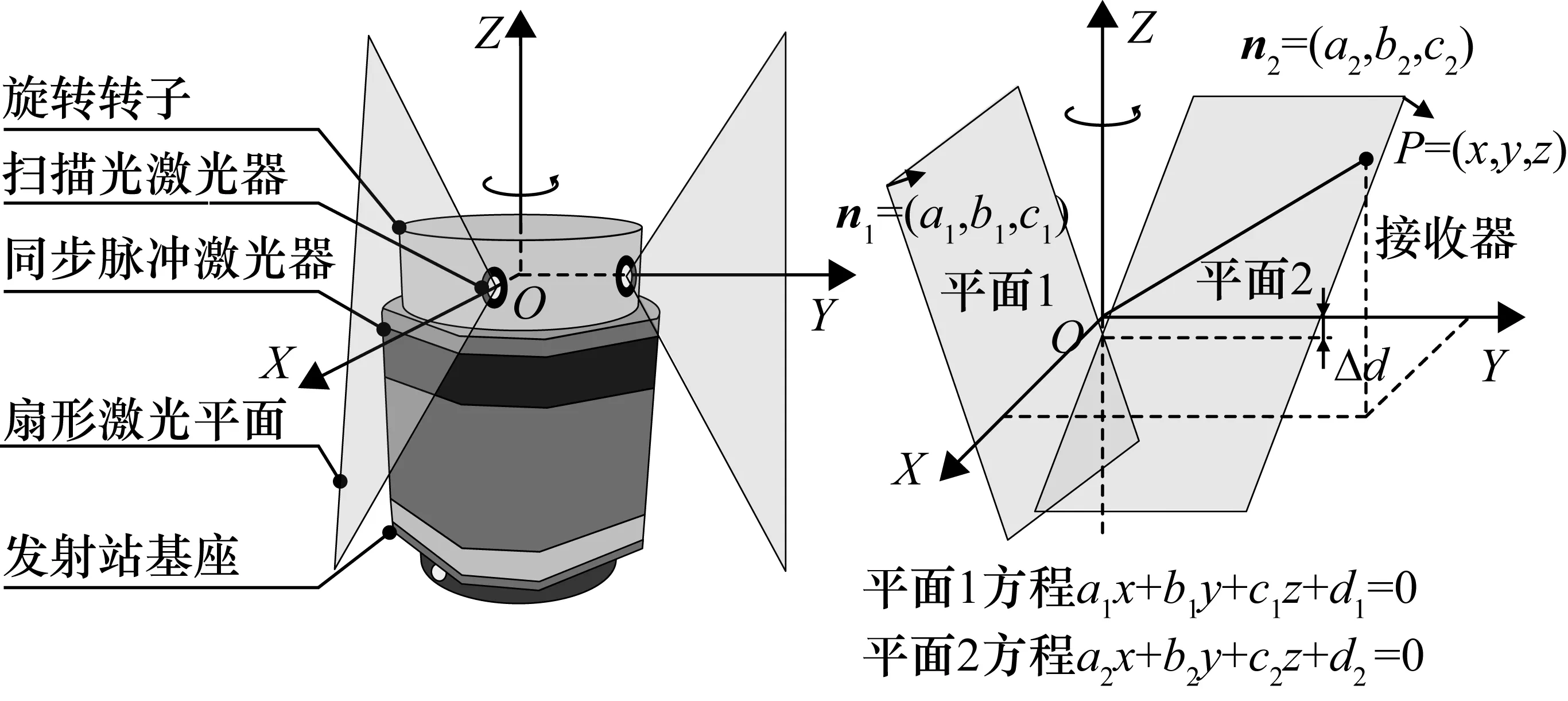
图3 室内GPS发射站结构及数学模型

当两激光扇面分别扫过接收器时，可计算光平面旋转角度θ1,θ2，即扫描角。发射站两个旋转激光平面方程在自身坐标系下的方程参数为

(4)

式中,

(5)

(6)

式中，i为发射站编号；j为激光扇面编号；[xkykzk]T为全局坐标系下的待求点三维坐标；Ri和Ti为全局组网定向的结果，它代表全局坐标系到发射站i局部坐标系的转换关系。

由两种系统的数学模型可知，仪器站位的位姿关系是测量网络中的重要参数，而组网的目的就是获取准确的位姿参数，是测量网络精度的重要保证。

2 协同组网方法

协同组网问题可具体为测量网络内具有多台激光跟踪仪、多台室内GPS发射站及若干测量点，通过优化算法实现测量网内所有站位的位姿和所有测量点位的坐标解算，示意图如图4所示。为实现两种系统的协同测量，必须引入相对约束完成组网。为提高算法的精度，采用一维距离约束和三维坐标约束两种约束构建方法，同时约束方程的构建是依照系统的不同传感单元进行高度耦合完成。因此，测量网内必须包括基准尺或三维控制场。具体的组网思路是，激光跟踪仪和室内GPS分别测量基准尺和三维控制场，依照仪器本身测量模型构建基本约束方程，同时通过基准尺的一维距离约束和三维控制场的坐标约束构建相对约束方程，通过迭代优化算法求解由基本方程和相对约束方程构建的最优化方程组，并通过设计合理的迭代初值求解算法完成最终组网。

图4 基于激光跟踪仪和室内GPS协同组网模型

2.1 协同组网模型

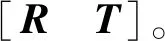
激光跟踪仪的约束方程可先将控制点转换到跟踪仪坐标系下：

(xlaser,ylaser,zlaser)T=Rlaser(xm,ym,zm)T+Tlaser

(7)

式中，(xlaser,ylaser,zlaser)T表示跟踪仪局部坐标系下的点，代入式(2)中，即可算出对应的观测量，因此每个跟踪仪站位可构建以下约束方程：

(8)

式中，带*标志的是由最终优化点反算回去的观测值，不带标志的为仪器观测值。

室内GPS的约束方程也是同样将控制点全局坐标转换到室内GPS局部坐标下：

(xGPS,yGPS,zGPS)T=RGPS(xm,ym,zm)T+TGPS

(9)

结合1.2节中室内GPS数学模型，并依照式(6)，每个室内GPS发射站均可列以下的约束方程：

(10)

协同测量网络中的一维基准尺是两端各有测量点同时两点距离l已知的标准器，因此，可以列以下约束方程：

(11)

求解过程需要达到H1,H2,H3共3组约束方程的最优结果，可以采用罚函数法构造以下最优化函数求解：

(12)

式中，λ1,λ2代表惩罚因子。每台仪器均有3个未知参量，共有3(I+J)个未知量。每个点位均可有3个跟踪仪方程，2个室内GPS方程；每个基准尺有一个距离约束方程。因此，总共约束方程的个数为：3IM+2JM+K。当方程数大于未知量数，即满足3IM+2JM+K>3(I+J)时，可采用Levenberg-Marquardt算法进行求解，得到每个站位的位姿参数，完成组网[15]。

2.2 迭代初值求解方法

Levenberg-Marquardt算法是一种兼具梯度法和牛顿法的优点的非线性最小二乘算法，其收敛速度快、稳定性好[16-18]。但是，采用Levenberg-Marquardt算法必须采用合适的迭代初值，否则易造成迭代不收敛而影响算法精度和速率。算法中的迭代初值主要包括激光跟踪仪和室内GPS每个站位初始的位姿参数。其中激光跟踪仪可直接进行点位测量，可通过多点的坐标系转换方法完成迭代初值获取[19]。室内GPS是多站位系统，只有角度观测值，需要采用一种基于后方交汇的迭代初值计算方法，依据系统局部坐标系与全局坐标系的点一一对应并且对应点的连接射线交汇于一点来构建约束方程[20]，示意图如图5所示。测量系统局部坐标系下的点a，b，c与全局坐标系下的A，B，C是一一对应关系，其连线交汇于空间点S，可利用这一约束完成迭代初值求解。考虑到每个发射站的初值获取方式一致，下面以单发射站为例阐述迭代初值估计过程。

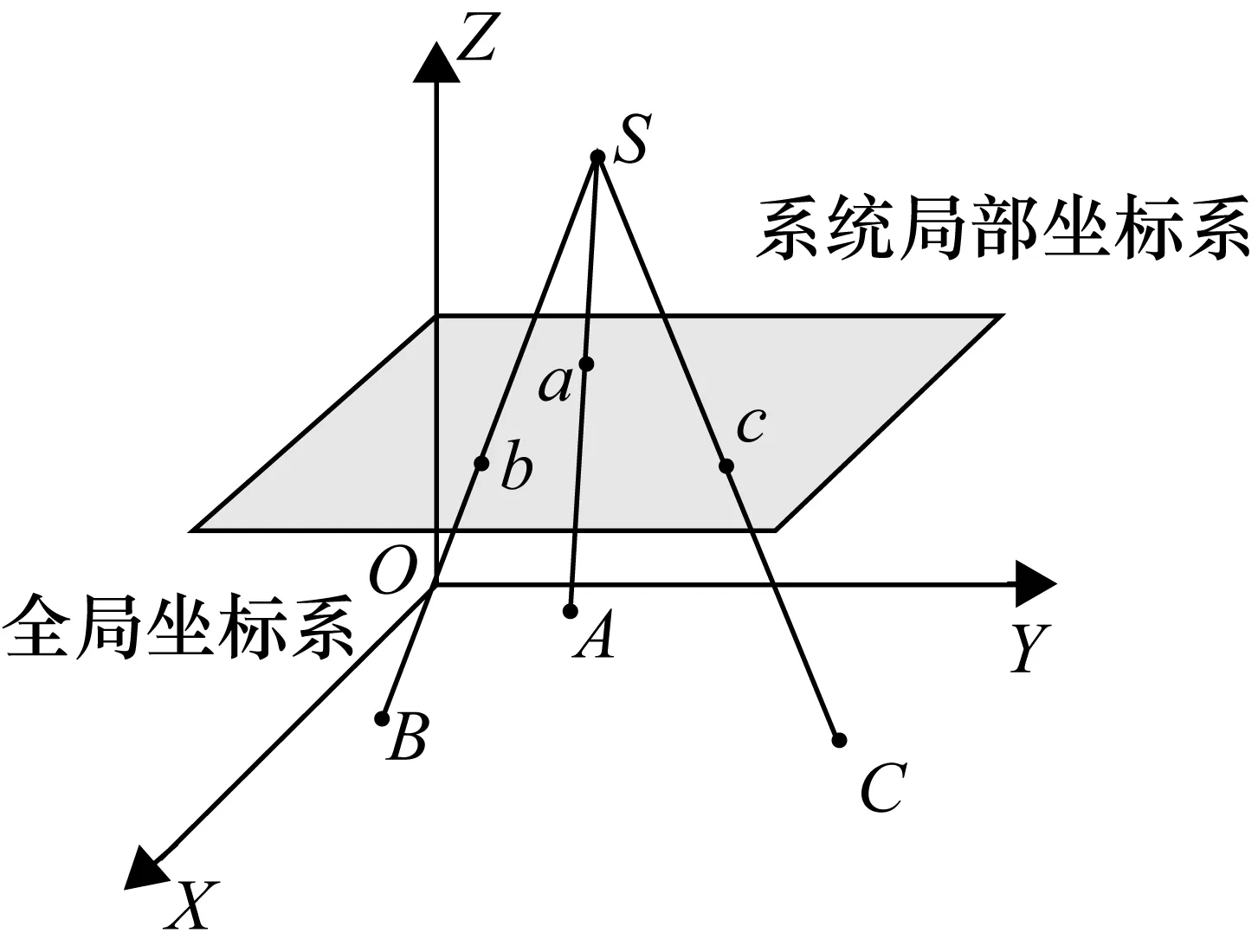
图5 基于后方交汇方法的迭代初值计算方法

根据数学模型，约束方程可以写成以下矩阵形式：

AX=0

(13)

其中，

是一个2m×12的系数矩阵。

作为未知参数， 将未知量X分解为

则方程可表示为

BX9+CX3=0

(14)

根据正交矩阵的特性‖X3‖2=1，最优化方程可写为

CR=‖BX9+CX3‖2+λ(‖X3‖2-1)

(15)

式中，λ为任意实数，将方程展开可以得到：

(16)

分别求CR求X9和X3的偏导函数，偏导函数值为0，方程为

(17)

将方程组化简为

(18)

式中,D=CTC-CTB(BTB)-1BTC，是个3×3的矩阵。X3是矩阵D的特征向量，从而可以解出X3，将X3带入第二方程即可解出X9，从而得到迭代初值。将迭代初值带入最终优化方程完成组网。

3 实验

为验证协同组网方法的性能和精度，在工业现场某厂房设计了以下实验。该实验面向工业现场条件下某部件模拟对接的任务中的组网过程，考虑现场条件，采用激光跟踪仪AT402和室内GPS组成协同测量网络，利用第2节的方法优化解算所有激光跟踪仪和室内GPS的站位位姿，可利用激光跟踪仪完成关键点位测量，室内GPS完成部件实时跟踪测量，实现两种仪器统一基准下的精确测量，可完成测量任务中的所有功能要求。实验现场如图6所示，实验中采用一台激光跟踪仪和两台室内GPS发射站组成协同测量网络，并利用基准尺进行精度验证。

图6 现场条件下协同测量实验图

为了验证激光跟踪仪和室内GPS协同测量网络的精度，在12 m×12 m×2 m的工作区域内随机布置10根基准尺，要求基准尺包含水平竖直纵深各个方向，基准尺两端的距离参量作为标准值，通过测量基准尺两端点位坐标算出距离值，该距离值与标准值进行比较，以差值大小作为评价网络精度优劣的标准。具体比对结果如图7所示。

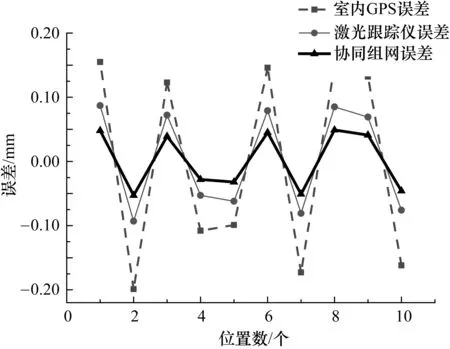
图7 精度对比结果

图7中包括3组数据，其中虚线代表单采用室内GPS测量的比对结果,细实线代表单采用激光跟踪仪的比对结果,粗实线代表室内GPS与激光跟踪仪协同测量的比对结果，以上的结果均针对同一测量对象。由实验数据可以看出，单采用室内GPS测量误差优于±0.200 mm，单采用激光跟踪仪的测量误差优于±0.100 mm，采用协同测量手段的结果优于以上两种方法，数据显示其测量误差优于±0.06 mm。数据证明了协同组网的方法能够提高网络测量的精度，具有高精度和高效率的优点。

4 结束语

针对单一系统在测量范围、精度和效率上难以满足现场需求的问题，采用一种基于激光跟踪仪与室内GPS的协同测量方法。在研究两种系统的数学原理前提下，提出了一种基于两种仪器不同传感单元的约束方程组构建方案，同时为提高网络的整体精度，在空间内引入了一维基准尺和三维控制场，以一维基准尺的距离和三维控制场的坐标作为相对约束构建方程，形成了最终带有惩罚因子的罚函数最优化方程。采用了基于后方交汇原理的迭代初值获取方法，使用Levenberg-Marquardt算法完成求解，最终实现了激光跟踪仪与室内GPS的协同测量。使得测量网络具备了激光跟踪仪的高精度和室内GPS的高效率的特点，实验数据表明协同网络的精度优于±0.06 mm，证明了组网方法的精度，具备较大的推广价值。值得注意的是，测量网络中激光跟踪仪和室内GPS站位的布局也会影响组网精度，在未来可通过研究布局优化算法进一步提高测量网络精度。