流形学习研究现状分析

张韬

摘 要：流形学习的目的就是对高维样本点集进行非线性降维，从中挖掘出样本点集的有效特征。本文主要对流形学习算法的研究现状进行分析，从中指出其存在的潜在问题，以及对未来的研究方向进行分析探讨。

关键词： 流形学习;样本点集;降维;算法

中图分类号：TP181 文献标识码：A 文章编号：1671-2064（2019）14-0203-03

0 引言

随着社会的发展， 目前已经进入到数据时代， 大数据这个概念被很多的人所认识。数据时代我们面临的数据量越来越大， 且数据的复杂度越来越高。这样存在一个很突出的问题， 当我们对大数据进行处理时， 会造成处理的时间及成本代价很高。另外， 通常在对数据进行学习之前， 需要对数据进行预处理， 即对数据进行清洗。所谓清洗， 就是将无用的信息剔除掉， 将有用的信息保留。常用的方法就是对数据集进行特征提取， 根据学习的需求， 从中提取有用信息。

通常情况下， 数据点集的维度很高， 每个维度都表示数据的一个特征， 从多个特征中提取少量特征， 其实质就是对样本点集进行降维。常见的降维方法有线性降维算法， 其主要目的是通过学习一个线性降维映射， 将高维样本点集投影到低维空间。常见的线性降维算法有P C A [ 9 ] 、MDS[8]、LDA[10]。主成分分析法（PCA）是最著名的线性降维算法， 其采用统计学的思想， 通过构造样本点集之间的协方差矩阵来分析样本点的分布特点。通过对协方差矩阵进行特征值分解， 按照特征值的大小对特征向量进行排列。最大的特征值所对应的特征向量表示第一主成分， 它表明，样本点集沿着此方向分布最多。依次可以构造第二主成分， 第三主成分等。通过这样的方式， 可以达到对样本点集进行降维的目的。多维尺度分析（ M D S ） 是另一类比较经典的线性降维算法， 其采用几何学的知识， 希望在降维过程中保持高维样本点之间的欧氏距离， 也就是说降维后， 低维样本点之间的欧氏距离与对应的高维样本点之间的距离保持一致。因此M D S 算法的关键是求解样本点之间的距离矩阵。第三个比较经典的线性降维算法是线性判别分析法（ L D A ） ， 这个算法主要用在分类学习中。对于带有标签信息的样本点集， L D A 算法的目的是让同一类的样本点映射后距离较近， 而不同类样本点映射后距离尽可能的远。这三类样本点在处理样本点呈现出线性分布结构时， 它们的降维效果非常的好。然而现实生活中， 由于通常处理的数据量非常的大， 而且数据的维数非常的高， 因此样本点集在高维空间中呈现出高度非线性分布结构。而针对这种分布特点的样本点集， 常见的线性降维算法已经无法精确的来提取其有效特征。因此， 基于此目的， 研究者提出一类非线性降维方法。

首先针对非线性分布的样本点集， S c h o l k o p f等人引入核函数的思想， 提出核化主成分分析法（ K P C A ） [ 1 1 ] ， 这个方法的主要思想是将核函数加入到样本点集上， 首先利用核函数， 将初始样本点集映射到更高维空间中， 使得样本点集在更高维空间中呈现出线性分布特征， 然后再利用P C A算法对更高维的样本点集进行线性特征提取。这个方法存在的问题是， 如何选择非线性核函数是算法的难点。因此，为了避免这个方法的局限性， 在2 0 0 0 年《科学》杂志上提出了流形学习的思想， 也就是假设一组非线性分布的高维样本点集分布在一个低维子流形上， 然后利用流形的性质对样本点集进行特征提取。从直观上理解， 流形是局部具有欧氏空间性质的几何空间， 也就是流形上每一点的局部邻域与欧氏空间的某个子集之间存在同胚映射关系， 因此从局部上借助于欧氏空间的性质对高维样本点集进行降维。流形学习首次引入了局部化的思想。

1 流形学习

下面我们对几类经典的流形学习算法进行分析， 从中来分析其存在的一些優点及局限性。流形学习首次将局部化的思想引入到机器学习中。其基本思想是从样本点集的局部邻域出发来获取其潜在的有效特征。因此流形学习的首要任务是对高维样本点集进行邻域划分， 常见的邻域划分的方法有两种， 一种是K - 近邻法， 一种是ε- 球邻域法。（ 1 ） K -近邻法[ 7 ]的基本思想如下： 首先任意选取一个样本点， 其次计算其与其余样本点之间的欧氏距离， 然后对这组欧氏距离进行排序， 选择距离最近的K 个样本点作为其最近邻点。

（ 2 ）ε-球邻域法的基本思想如下： 首先仍然是任意选取一个样本点， 然后以这个样本点为中心， ε为球半径做一个球面， 球面内部的样本点就称为此样本点的球邻域点。为了分析的方便， 在此假设高维样本点集表示为{ x 1 ，x 2 ， …， x N} ， x i∈R D ，其中N表示样本点集的个数， D 表示样本点集的维度。降维后对应的低维空间的样本点集表示为{ y 1，y 2，…，y N} ，y i∈Rd，d表示低维空间的维度。

1.1 等度量映射（ISOMAP）

ISOMAP[2 ]是在20 00年提出的流形学习算法，它引入了流形学习的概念。其基本思想是以线性降维M D S 算法为基础， 通过获取高维样本点集之间真实的测地线距离来代替两点之间的欧氏距离。在流形上， 任意两点之间的真实距离通过测地线距离来表示。因此I S O M A P 算法的主要思想是获取任意两个样本点之间的测地线距离， 然后利用M D S算法， 在低维空间重构一组样本点集， 使得在低维空间任意两点之间的欧氏距离等于高维样本点之间的测地线距离。算法的具体步骤表示如下：

第一步： 利用邻域划分算法对高维样本点集{ x 1 ，x 2 ，…， x N} 进行邻域划分。

第二步： 在样本点集上构造局部邻接图， 利用D i j k s t r a算法[ 6 ] 计算任意两点之间的最短路径， 邻域点之间的最短路径表示为两点之间的欧氏距离。

第三步： 利用M D S 算法以及第二步求得的样本点之间的距离矩阵，在低维空间重构一组样本点集{ y 1 ，y 2 ，…，y N}。

1.2 局部线性嵌入（LLE）

LLE[2]算法与ISOMAP算法同年发表在《科学》杂志上的另一篇流形学习算法。它与I S OM A P算法的出发点不同， 它的主要目的是在降维过程中保持样本点集之间的局部几何结构。因此它属于保局部结构的算法。L L E 算法的基本思想是假设流形的局部邻域为线性空间， 邻域内的中心点可以由它的邻域点集进行线性表示， 其对应的线性相关系数表示邻域点之间的局部几何结构。L L E 降维的目的是在低维空间重构一组样本点集， 使得样本点集对应的局部邻域样本点之间仍然满足这个线性相关系数。下面给出算法的具体步骤：

第一步： 仍然是利用邻域划分方法对高维样本点集进行划分。

第二步： 以样本点x i 的邻域为例来说明， 计算邻域中心点与其邻域点之间的线性相关表示系数。

第三步： 在低维空间重构一组样本点集， 使得对应的邻域点之间满足高维样本点之间的线性相关性。

1.3 拉普拉斯特征映射（LEM）

L E M [ 3 ]是另一类经典的流形学习算法， 它也属于保局部特征的降维学习算法。其基本思想是希望降维后距离较近的点仍然距离很近， 因此在邻域点之间赋予权值， 利用权值来表示两点之间的相似度， 权值越大表示两点之间的相似度越高。算法的基本步骤表示如下：

第一步： 利用邻域划分方法对高维样本点集进行邻域划分。

第二步： 构造邻域点之间的权值， 在此利用高斯函数来计算邻域点权值。对于非邻域点之间的权值赋予零。第三步： 利用第二步求得的邻域点之间的权值， 在低维空间重构样本点集， 使得距离越近的点， 在低维空间中仍然距离越近。

2 流形学习现存问题分析

第二节， 我们只对流形学习的三个经典的算法进行了详细的介绍， 由于流形学习属于无监督学习的范畴， 因此在这十几年当中， 流形学习得到了迅速的发展， 除了这三类经典的算法以外， 流形学习又发展了一系列经典的算法，例如HLLE[1 4]、LTSA[1 2]、LPP[1 3]算法等。下面我们来分析一下这些算法所存在的一些问题。

通过对这些算法进行分析可以看出， 流形学习算法的一个共有的前提假设是所处理的高维样本点集分布在某个低维子流形上， 这个子流形是嵌入在高维空间中的。除此之外， 针对每个算法又有各自特有的假设条件。例如I S O M A P 算法假设所处理的流形为一个无洞的凸子集， 并且流形是与欧氏空间之间等距同胚的。另外L L E 以及H L L E 、L T S A 等算法假设样本点的局部邻域是线性空间。这些假设存在如下一系列问题。

（ 1 ） 针对分布呈现出非线性结构的流形， 例如球面， 假设局部邻域为线性空间就会存在问题。

（ 2 ） 在进行邻域划分的时候， 是在每个点都进行邻域划分， 这样就导致邻域集的个数与样本点的个数保持一样。对于大数据级别的数据量， 会导致构造的邻域的个数过大， 使得算法的复杂度非常的高。

（ 3 ） 在对子流形的低维维度进行估计时， 由于假设局部邻域为线性空间， 这样会导致估计存在偏差。

针对以上存在的这些问题， 近些年来， 已经有一些改进的算法，例如MLLE算法[5]是对LLE算法进行改进，使得所选取的邻域点更合理。TCIE算法[4 ]是对ISOMAP算法进行改进， 这个算法消除了I S OM A P算法对流形凸假设的条件。尽管又发展了一系列改进的算法， 但是这些算法本身仍然存在一些未被解决的问题。例如， 已有的流形学习算法仍然未考虑流形局部的弯曲程度， 即曲率信息。在对邻域进行划分时并未考虑样本点的分布特点。因此， 在接下来的工作中， 可以将流形本身的拓扑结构加入到流形学习算法中， 从本身的结构出发来设计算法。

3 实验分析

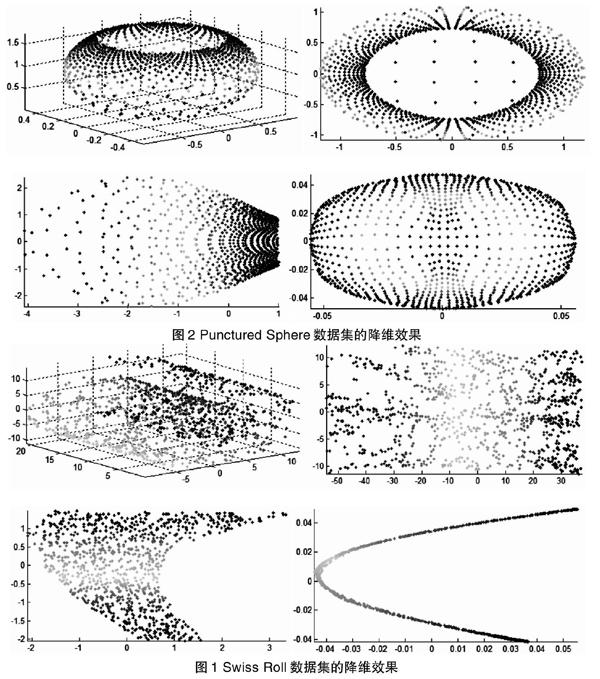
在本实验中， 我们主要采用一组三维合成数据集来进行实验， 从中分析已有的流形学习算法所存在的一些问题。在此， 我们主要选取了两组数据集来进行实验， 一组是分布呈现出瑞士卷结构的三维数据集（Swis s Roll），一组是球面数据集（Punctured Sphere）。

在实验设计中，我们主要采用I S OMAP、L LE以及L EM三个流形学习算法对这两组数据集进行降维， 从中分析算法的降维效果。具体的可视化结果表示如图1 ， 图2 所示。每个图有四个子图， 从左到右分别表示初始数据集， I S O M A P算法降维效果， L L E 算法降维效果， L E M 算法降维效果。从这两个图可以看出， 它们的降维效果并没有达到最好， 例如，针对Swis s Roll数据集，LLE算法以及LEM算法的降维效果就不好， 究其原因是因为在降维过程中并未考虑样本集分布的弯曲程度。

4 结语

本文主要對流形学习的几类算法进行解释， 从中分析不同算法所存在的主要问题。在实验方面， 选取了两组数据集在不同的流形学习算法上进行实验， 实验结果也印证了我们所分析的当前流形学习所存在的问题。

参考文献

[1] S. Roweis and L. Saul， Nonlinear dimensionality reductionby locally linear embedding. Science， vol.290，2000.

[2] J. B. Tenenbaum， V. de Silva and J. C. Langford， Aglobal geometric framework for nonlinear dimensionalityreduction. Science， vol.290，2000.

[3] M. Belkin and P. Niyogi， Laplacian eigenmaps and spectraltechniques for embedding and clustering. In proc.Int. Conf. Advances in Neural Information ProcessingSystems，2001.

[4] G. Rosman， M.M Bronstein， A.M. Bronstein， and R. Kimmel.Nonlinear dimensionality reduction by topologically constrainedisometric embedding. Int. J. Comput. Vis.89：56-68，2010.

[5] Z. Zhang， J. Wang. Mlle： modified locally linear embeddingusing multiple weights. NIPS 19：1593-1600，2006.

[6] E.W. Dijkstra. A note on two problems in connectionwith graphs. Numerische Mathematic， 1：269-271. Doi：10.1007/BF01386390.

[7] T.M. Cover and P. E. Hart. Nearest neighbor patternclassification. IEEE Transactions on Information Theory，13（1）：21-27，1967.

[8] M.A.A. Cox， T.F. Cox， Multidimensional scaling. In： Handbookof Data Visulization，315-347，2008.

[9] Lindsay T Smith. A tutorial on principal componentsanalysis. February 26，2002.

[10] R. A. Fisher. The use of multiple measurements intaxonomic problems. Annales of Eugenics，7（2）：179-188，1936.

[11] J. Yang， A.F. Frangi， J.-Y. Yang， D. Zhang， and Z. Jin.KPCA plus LDA： a complete kernel Fisher discriminantframework for feature extraction and recognition. IEEETrans Pattern Analysis and Machine Intelligence， vol. 27，no.2，pp. 230-244，2005.

[12] Z. Zhang， H. Zha. Principal manifolds and nonlineardimension reduction via local tangent space alignment.SIAM J. Sci. Comput.26：313-338，2004.

[13] Xiaofei He and Partha Niyogi. Locality preservingprojection. Int. Conf Advances in Neural Information ProcessingSystems，2003.

[14] D.L. Donoho， C.E. Crimes. Hessian eigenmaps： locallylinear embedding techniques for high-dimensional data.Proc. Nati. Acad. Sci. USA 100：5591-5596，2003.