曲线段箱梁采用单梁模型计算时梁顶与支座顶约束刚度模拟取值的讨论

严宇濛

（上海市政工程设计研究总院（集团）有限公司，上海市 200092）

0 引言

城市扩张建设过程中，在城市道路中曲线段上的桥梁越来越多，越来越常见。曲线段上弯桥的受力特性与直线桥梁有明显区别，不仅要考虑弯扭耦合效应，支座反力的分布也存在较大的差异。现有以往的已建工程来看，弯桥的计算模拟仍然是需要进一步进行讨论研究的。本文基于重庆市某位于曲线段上的现浇弯桥进行讨论，对整桥采用单梁计算，分析自重引起的偏载，车辆偏载，以及梯度温度和整体升降温，对有限元计算中主梁与支座顶约束刚度的模拟取值进行试算，得出不同的反力结果与梁格模型进行计算得出的反力结果进行比较，对提出的主梁与支座顶约束的简化模拟方法的适用性进行讨论。

1 项目概况

根据道路的平面、纵断面及横断面设计，为该段道路段需跨越的河道，采用桥梁的结构形式减少对行洪的影响，桥梁工程的布置主要为30 m+37 m+30 m，见图1。上部结构为预应力混凝土连续箱梁桥，下部结构为柱式墩，嵌岩桩。桥梁沿里程前进方向位于纵坡为4.4%上坡段，横坡为双向横坡，均为1.5%。桥梁位于道路平曲线上，半径为200 m，半径较小，为增强其抗扭性能及整体稳定性，与1号轴处采用墩梁固结。桥梁宽度26 m，宽跨比较大，箱梁梁高2.0 m，采用单箱多室断面，见图2。箱梁翼缘悬挑2.5 m，顶、底板厚0.25 m，腹板跨中处宽度0.5 m，为增强支点处箱梁的抗剪能力，支点附近腹板宽度渐变为0.9 m。桥梁支座均采用GPZ（Ⅱ）型盆式橡胶支座，盆式支座底盆横向沿桥台轴线设置，盆塞及上支座板纵向沿桥轴线方向设置。

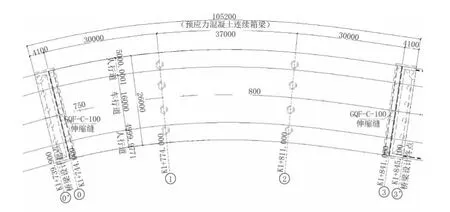
图1 平面图（单位：mm）

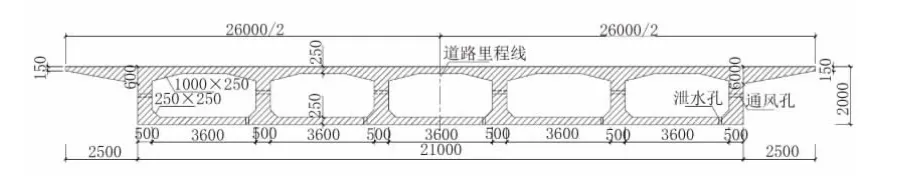
图2 断面图（单位：mm）

2 单梁计算模型

采用midas-civil进行计算，计算跨径为30 m+37 m+30 m，计算中所取用的二期恒载根据实际情况计算，汽车荷载采用城－A级，汽车荷载冲击系数按行业设计规范[1]进行计算。桥梁结构因温度作用引起的效应共分为均匀温度作用和梯度温度作用两个部分。其中均匀温度作用按结构整体升温20℃及结构整体降温15℃来考虑，梯度温度作用按行业设计规范进行输入。

边界条件上除了模拟固结墩以外，下部结构均没有模拟，支座模拟刚度均采用常规数量级刚度进行模拟，通常建模中，梁顶与支座顶的连接采用软件中的弹性连接的刚接进行模拟，本文分别采用弹性连接的刚接（模型1）和弹性连接中的一般连接即赋予一定刚度（模型2）分别进行试算。主梁采用7自由度单梁模型进行建立，模型见图3。

对于模型2，支座顶与梁顶各个方向的刚度采用实际横梁的截面尺寸与混凝土弹性模量与剪切模量进行计算：

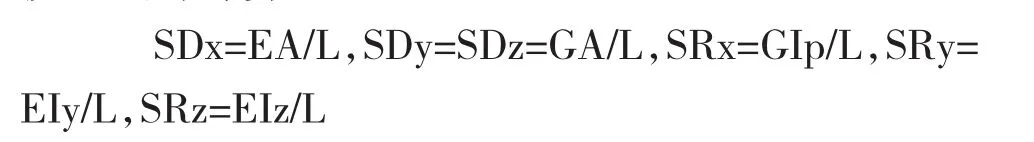
其中E为混凝土弹性模量，A为横梁截面面积，G为混凝土剪切模量，L为梁顶节点位置与支座位置实际距离，Ip为横梁横断面抗扭惯性矩，Iy，Iz为相应方向横梁截面抗弯惯性矩，SDx为单元局部坐标系下相应方向轴向抗压线刚度，SDy、SDz为单元局部坐标系下相应相应方向剪切线刚度，SRx为单元局部坐标系下相应方向扭转线刚度，SRy、SRz为单元局部坐标系下相应相应方向抗弯线刚度。

图3 单梁模型图

对于模型1和模型2，支座刚度均采用盆式支座常规刚度数量级进行模拟。表1为模型2边界条件刚度的计算结果。

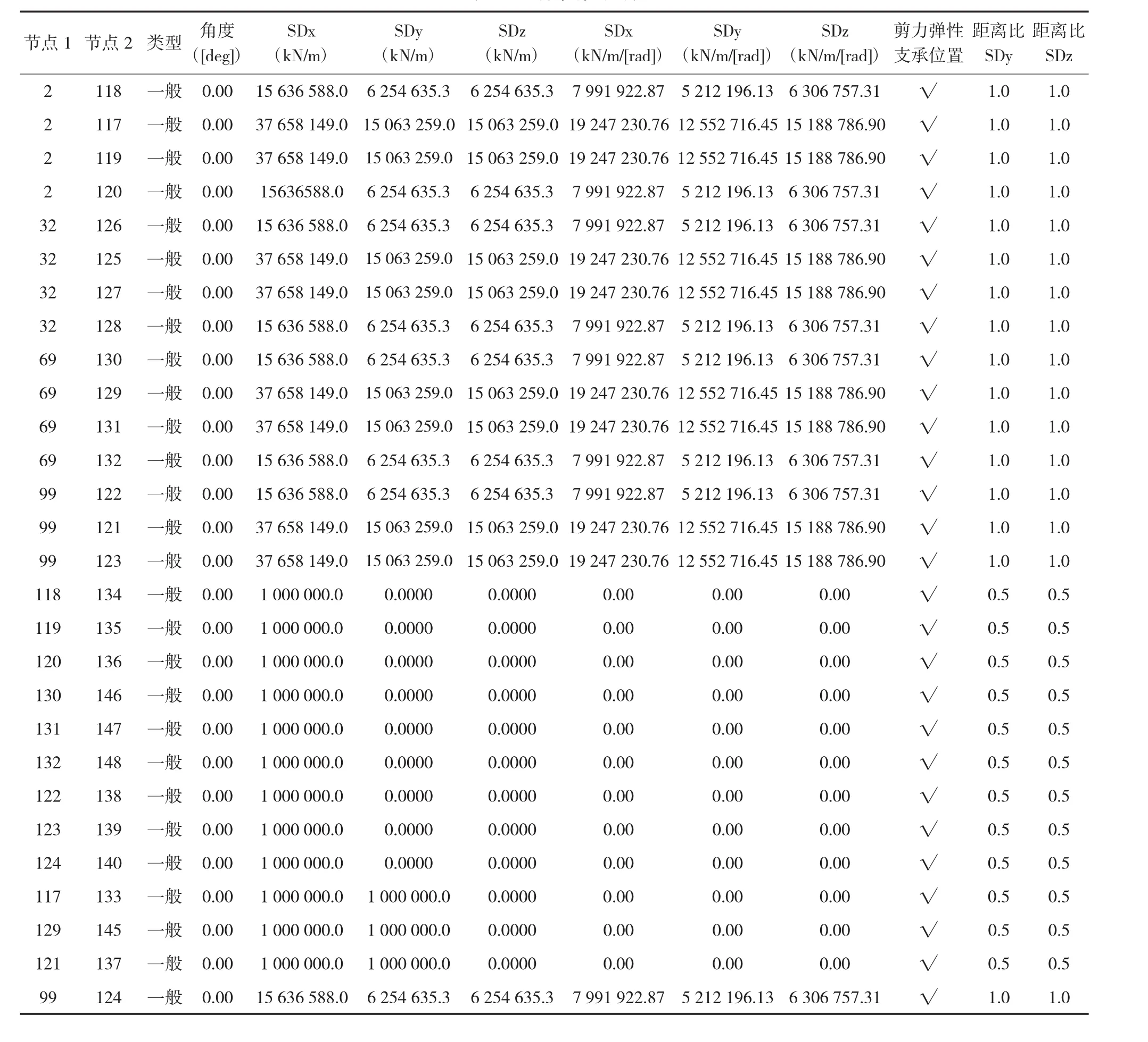
表1 边界条件刚度表

其中梁顶与支座顶约束剪力弹性支承位置，根据软件计算原理，距离比SDy、SD座均取值1，即考虑在荷载作用下传递剪力引起的弯矩，更好的模拟实际受力情况。

3 梁格计算模型

箱梁沿横向根据腹板数量共划分为6片纵梁（模型3），基于已有的研究，梁格法的梁格划分及分析方法对于曲线宽箱梁桥是可行的[2]。全桥共划分359个单元，在有支座位置的附近，采用弹性连接的刚接对支座顶与就近纵梁进行连接。在支座位置调整局部坐标系，保证和实际支座受力特征相同。荷载工况同单梁模型，模型见图4。

图4 梁格模型图

4 支座反力分析

为做统一比较，3个模型均采用相同的荷载组合进行反力分析，根据计算结果，单梁模型中不同约束条件下反力结果和梁格模型下反力结果分别见图5～图 7。

图5 模型1反力图

图6 模型2反力图

通过计算结果分析，模型1每个轴沿横向反力的分布变化趋势均是单一变大或变小，模型2和模型3的变化趋势较一致，不均匀性更大。

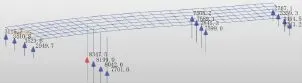
图7 模型3反力图

模型1梁顶与支座顶刚接约束，程序采用一个极大刚度对梁顶节点与支座顶节点进行连接，使两个节点自由度完全耦合，并且对于本桥多支座的情况下，即将几个支座顶节点与梁顶节点形成刚臂，在荷载作用下，横向反力的分配仅考虑距离效应，并没有考虑荷载根据横梁不同支座位置按线刚度分配荷载。模型2考虑了这一部分的区别，实际输入连接的刚度，在反力计算结果上更贴合实际，模型3直接根据横向联系的实际截面刚度进行荷载分配，计算结果也在三个模型中最合理。但三个模型在最大支座反力的计算结果上差别较小。

5 结 语

弯桥的反力分布较复杂，反力沿横向不均匀性较直桥有明显区别，因此在模拟计算过程中应重视。

在采用有限元软件用单梁模型对弯桥进行模拟计算时，对于梁顶与支座顶的连接方式，采用常规刚度模拟与实际情况的反力分布情况有较大可能存在一定的出入，也就对于最终的结构安全计算有一定的影响，本文仅通过单个桥梁进行比较，不具有广泛性，但在生产设计过程中，在简化模拟边界条件时应尽可能采用更合适的模拟方法进行复核。本文模型2采用的简化方法为其中一种方法，反力结果上较为接近梁格模型，但也存在一定的局限性和不足。对于不需要用梁格模型进行复核的情况下，可以一定程度上借鉴。