长短叶片对射流式自吸离心泵性能的影响

董亮，潘琦，刘厚林，代翠，徐建红，徐海良

(1.江苏大学流体机械工程技术研究中心，江苏镇江，212013；2.江苏大学能源与动力工程学院，江苏镇江，212013；3.君禾泵业股份有限公司，浙江宁波，315171)

由于自吸泵具有实现自吸、便于远程集中控制、实行自动化操作等优点，近几年来在农业、消防、市政、电力、矿山、化工等领域得到了普遍的使用，尤其适用于流动排灌、移动工作、启动频繁和灌液困难等场合。振动噪声和多工况高效平稳运行是制约射流自吸泵产业化的关键技术问题，所以，迫切需要创新家用水泵的相关技术，开发出高性能、低噪声和高可靠性的新一代家用水泵产品，以提高我国家用水泵的整体设计和生产水平[1-3]。ROSSI 等[3-4]对射流自吸泵的应用及内部全流场进行研究。王常斌等[5]对射流泵湍流场进行数值模拟与试验，发现湍流主要出现在喉管入口处，但并未找到解决射流泵的能量损失的方法。刘建瑞等[6-7]通过数值计算，探讨了射流自吸泵自吸过程中泵体内气液两相流流动规律，并通过模拟试验相结合方式探索了射流喷嘴几何参数对喷灌泵自吸性能的影响。EAMES[8]以射流泵的能量交换原理为理论基础，提出高性能射流泵的优化设计方法。赵雪岑等[9]以面积比、喉管长颈与吼嘴距为参数对射流泵水力特优化，使得模型泵效率提高6%。王洋等[10-12]研究基于大涡模拟的射流泵内部非定常流动规律，通过数据拟合得到正交试验最优参数组合，优化模型在额定流量点效率提高约5%。由于喉管、吼嘴等部件是静止部件，本身处于不做功的状态，通过改变其结构而获得较大的优化比较困难，所以，要获得较为明显的优化，应着重研究叶轮做功部件。尽管许多学者对射流自吸泵进行水力优化来提高其性能，但大部分优化都只是针对射流部件，而由于定子部件不做功，很难在射流泵优化上尤其是水力性能的优化上取得重大突破。为此，本文以1台模型泵作为实验对象，通过优化叶轮后，对模型泵优化前后的外特性进行模拟与比较。目前采用大涡模拟湍流模型结合Lighthill声类比理论研究水泵流体动力噪声已经成为一种普遍方法[13]。DONG等[14]着眼于叶轮尺寸对离心泵噪声所产生的影响，并通过叶片之间设置短叶片以降低噪声。耿少娟等[15]通过数值方法研究无短叶片、有长短叶片和短短叶片3种叶轮的离心泵非定常流情况下的全三维流场，以研究离心泵噪声。袁寿其等[16]测试了叶轮参数及流量下的水动力噪声。刘厚林等[17-19]也利用此种方法研究了叶轮参数对离心泵流体噪声的影响。龙新平等[20]通过对喉管低压区进行补气来降低射流泵产生汽蚀时的振动与噪声。目前关于射流泵产生噪声的主要部件与产生噪声的原因仍然存在较大的争议，如何降低射流泵噪声依旧是急需解决的问题。为此，本文利用上述方法就额定工况下对不同叶片形式的射流自吸泵可能诱导噪声的部件分别进行内外场噪声计算与试验验证，从而得到模型泵贡献噪声最主要的部件与降低射流自吸泵噪声的方法。

1 研究对象

1.1 实验装置

试验在君禾泵业有限公司的试验台开展。图1所示为试验台现场示意图，试验装置包括水池、进出口水路管、射流自吸泵、电动机、电磁流量计、压力表、电动调节阀、水听器、泵产品参数测量仪及高性能数据采集系统等。

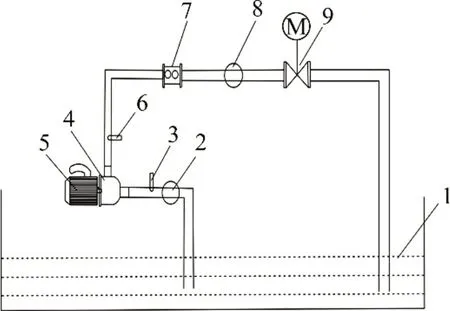
图1 试验台现场装置示意图Fig.1 Schematic diagram of device on site of test bench

采用INV3020C型高性能24位数据采集系统采集内声场噪声信号，然后对数据进行处理分析。对内声场噪声信号的测量选用RHSA-10 型水听器，其频率线性工作范围为20～100 kHz，灵敏度为188 dB。水听器的安装方式一般分为3种类型：内置式安装、平齐式安装和管道-容腔式结构。每种安装方式各有利弊，平齐式安装能够可靠地测量水管中脉动声场，同时对管中流场影响最小，不足之处是测量会受到管壁边界层噪声影响。冯涛等[21]认为边界层噪声相比脉动噪声量级很小，可认为水听器监测值即为泵内部流动噪声。且由于水听器灵敏度较高，容易受泵出口压力脉动影响，因此，需布置在远场端，一般位于距离泵出口法兰6～8倍管径处。故声场测点位置位于距离泵出口法兰8倍管径处，采用与管道平齐式安装法。

1.2 模型泵参数

原叶片与长短叶片的主要结构参数如表1所示。所用射流泵结构参数如下：叶片数Z为6片，叶轮进口直径D1为28.5 mm，叶轮出口直径D2为121 mm。其额定工况主要参数如下：额定流量Qd为2.4 m3/h，扬程Hd为14.5 m，额定转速n为2 750 r/min，额定功率P为800 W，比转速ns为34。

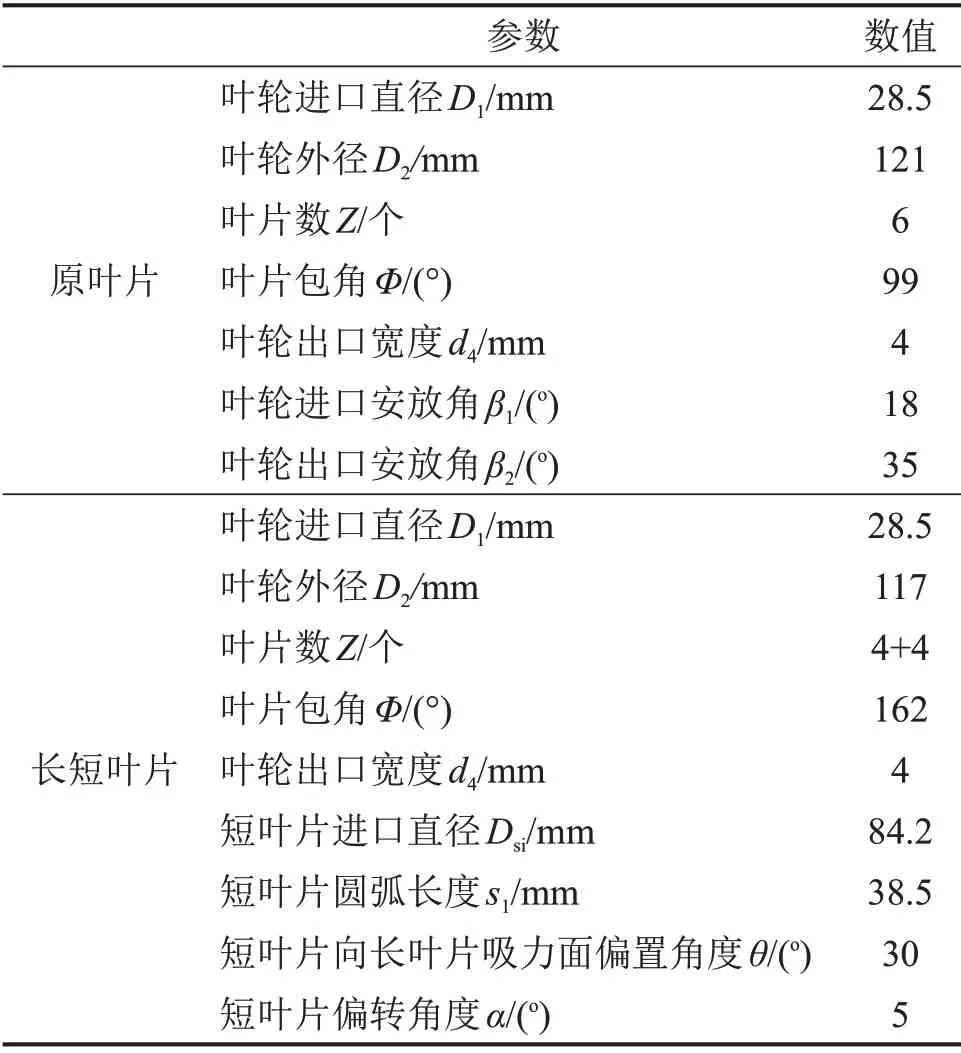
表1 射流自吸泵主要结构参数Table1 Main geometry parameters of the jet self-priming pump

由于需要在不改变现有设备条件的情况即功率与流量不变的情况下提高模型泵扬程，故选择对叶轮进行优化设计。本文叶轮叶片采用添加分流叶片形式，即所谓的长短叶片交叉布置，而添加分流叶片虽然提高了扬程，但功率也会随之增加，所以，必须在叶片参数上进行细化设计，采用4个长叶片4个短叶片交叉布置。而短叶片的相关尺寸参数是设计的着重点，由文献[1]可知，短叶片主要设计参数为短叶片进口直径Dsi、周向偏置度θ以及偏转角α。理论上，短叶片长度越长，扬程就会越高，而短叶片过长则会堵塞流道，扬程反而降低。通过多次的设计对比后，选择短叶片圆弧长度s1为38.5 mm，选择短叶片进口直径Dsi约为84.2 mm。本文采用短叶片向长叶片背面偏置的手段，这样有利于改善叶轮出口的流动情况。通过多次对比设计本文采用短叶片向长叶片背面的偏置角度θ为30°，短叶片偏转角度α为5。优化前后叶轮出口宽度不变都为4 mm，而外径由原来的121 mm减小到117 mm。图2所示为长短叶片设计二维结构图。

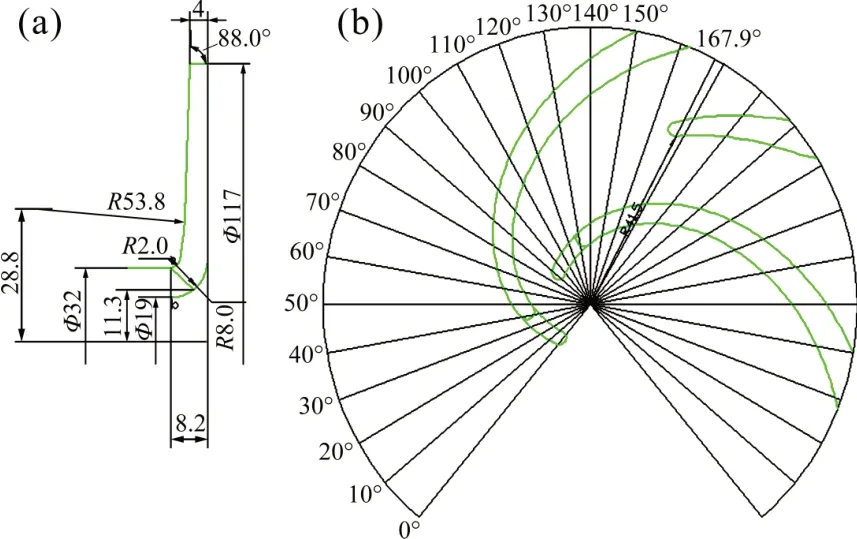
图2 长短叶片二维结构图Fig.2 Two-dimensional structure diagram of long and short blade

2 数值计算

2.1 建模以及网格划分

图3所示为射流式自吸泵的2 种不同叶片形式叶轮的三维水体剖面图。

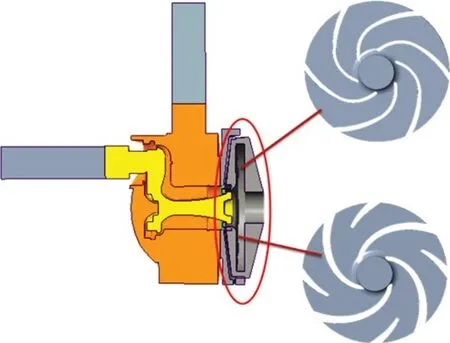
图3 射流自吸泵三维水体剖面图Fig.3 3D flow profile of jet self-priming centrifugal pump

将计算域导入CFD ICEM 进行网格划分，由于结构较复杂，采用适应度较强的非结构四面体网格，经过网格无关性检查最终确定网格数约为350 万个，可以保证数值计算准确性。

2.2 流场计算

利用流体计算软件CFX 对射流式自吸泵计算定常和非定常数值[24]，计算域包括6个部分：进口延长段、射流器水体、叶轮水体、导叶水体、腔体及出口延长段。其中，叶轮流场采用旋转坐标系，其余流场都设置为静止坐标系，边界条件分别设为进口为1.0132 5 kPa，出口为质量流量，壁面条件采用无滑移不考虑粗糙度壁面条件，湍流模型选取SST(shear stress transport)模型。在动静部件间使用交界面进行数据交换，其中对于定常计算，使用冻结转子交界面(frozen rotor interface)，而对非定常计算，采用瞬态动静交界面(transient rotor/stator interface)，网格关联采用GGI 方式；本文共选取计算0.2Qd，0.4Qd，0.6Qd，0.8Qd，1.0Qd及1.2Qd共6 个 工 况 流 场 信 息。计算收敛条件的收敛标准为残差小于10-4。

采用物理时间步进行定常计算，时间步长为3.636 4 ms，非定常数值计算中，时间步长设置ΔT为60.61 ms，即叶轮旋转1°所需时间。当流场呈现出明显周期性且达到稳定之后，提取8个旋转周期数据以作为噪声计算的激励源。

2.3 声场计算

整个计算过程均在LMS Virtual.Lab 平台实现，采用DBEM(direct boundary element method)求解声场[25]。在噪声计算过程中，利用快速傅里叶变换将时域脉动转换为频域脉动，并映射至声学网格。以加速度作为边界条件，进出口定义为全吸声属性，其余表面假设为全反射壁面，特性声阻抗Z=1.5×106kg/(m2∙s)，声速为1 500 m/s[26]。场点设置在距离泵出口法兰8倍管径处(与试验测点相同)，并进行声压级换算。本文通过对射流泵可能诱发噪声的部件分别计算，从而可以得出每个部件对模型泵所做的噪声比例[27-28]。通过模拟算出不同频率下定子部件与转子部件的声压后，最后通过总声压级Lp计算公式计算出各部件的总声压级以及泵体的总声压级。其中总声压级Lp计算公式为：

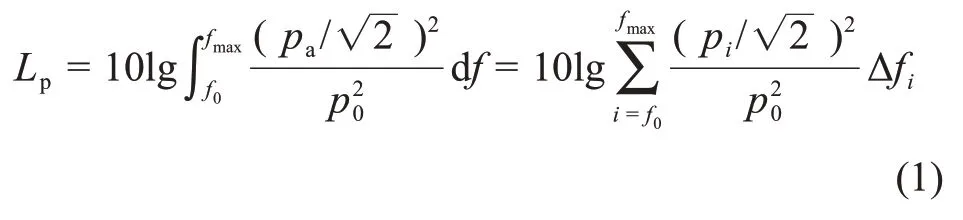
式中：Δfi为计算时最小分辨率；f0和fmax分别为计算频率的上限和下限；pi为有效声压，Pa；p0为参考声压，水中通常取1×10-6Pa。

由于射流泵结构的特殊性，本文在建立声学计算模型时，射流器部分需要单独建立模型，其他定子部件与叶轮所提供的噪声则利用相同模型来计算。本文声学面网格如图4所示。

为了获得离心式射流自吸泵外声场声压级在不同方向的分布情况，射流泵外部以泵体为中心设置直径1 m的标准圆场点并以泵出口中心线和轴心线交点为中心，分别在xy,yz和zx面建立1 m×1 m的声学监测面，在每个监测面上距中心1 m 处设置36 个间隔为10°的监测点。文献[22]表明由叶轮扇声源所产生的外场辐射噪声极小，可以忽略，因此，本文主要研究射流泵各定子部件额定工况下所产生的外场辐射噪声。图5所示为射流泵外场面场点及圆场点。

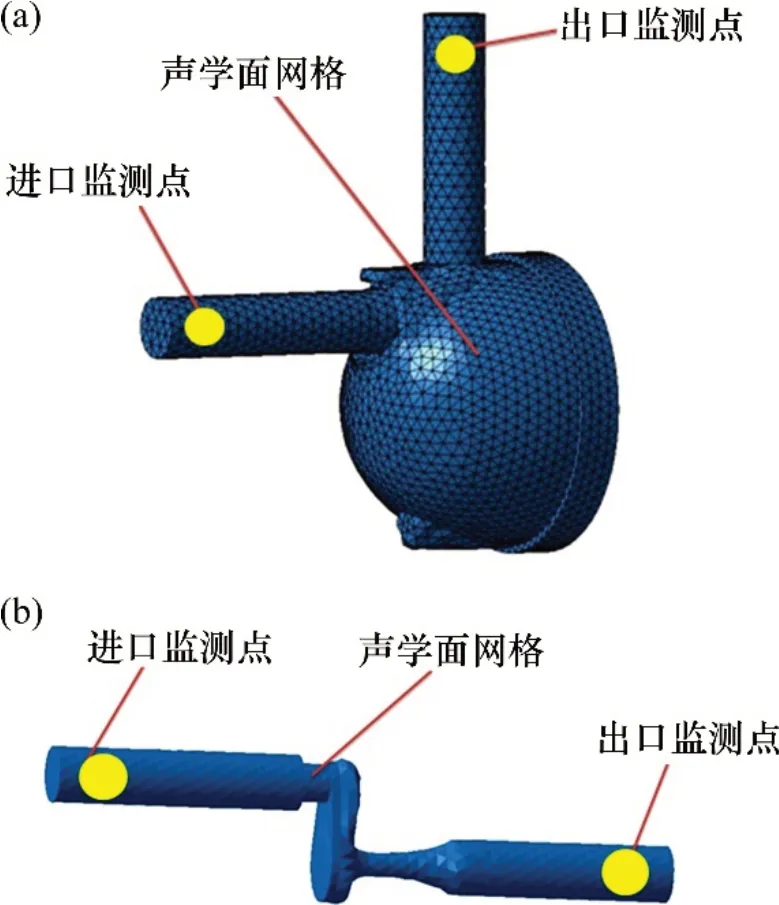
图4 声学面网格及测点Fig.4 Acoustic surface grids and measuring points

图5 模型泵外场面场点及圆场点Fig.5 Surface and circular field points of model pump

3 结果与讨论

3.1 外特性结果

图6所示为模型泵优化前后外特性曲线。由图6可见：模拟结果与实验结果都表明优化模型对比原模型在各个工况点的扬程都有明显提高。模拟结果与试验结果在小流量与大流量的工况下拟合效果比较差，这是射流泵结构的复杂性和极限工况的不稳定性所致。而在额定工况下(Qd=2.4 m3/h)，模拟结果与试验结果拟合较接近。在额定工况下试验数据优化模型扬程较原模型扬程提高12.6%，模拟数据优化模型扬程较原模型扬程提高11.63%；在0.8Qd下，试验数据优化模型扬程较原模型扬程提高14.28%，模拟数据优化模型扬程较原模型扬程提高13.0%；在1.2Qd下，试验数据优化模型扬程较原模型扬程提高20.5%，模拟数据优化模型扬程较原模型扬程提高19.6%。由上述结论可得额定流量点附近模拟结果与数值结果扬程变化相对误差皆小于2%，而大流量工况下相对误差小于5%。因此，预测结果与试验结果在扬程上升的比例方面基本一致，而模拟与试验的结果也表明优化模型较原模型提高了扬程。

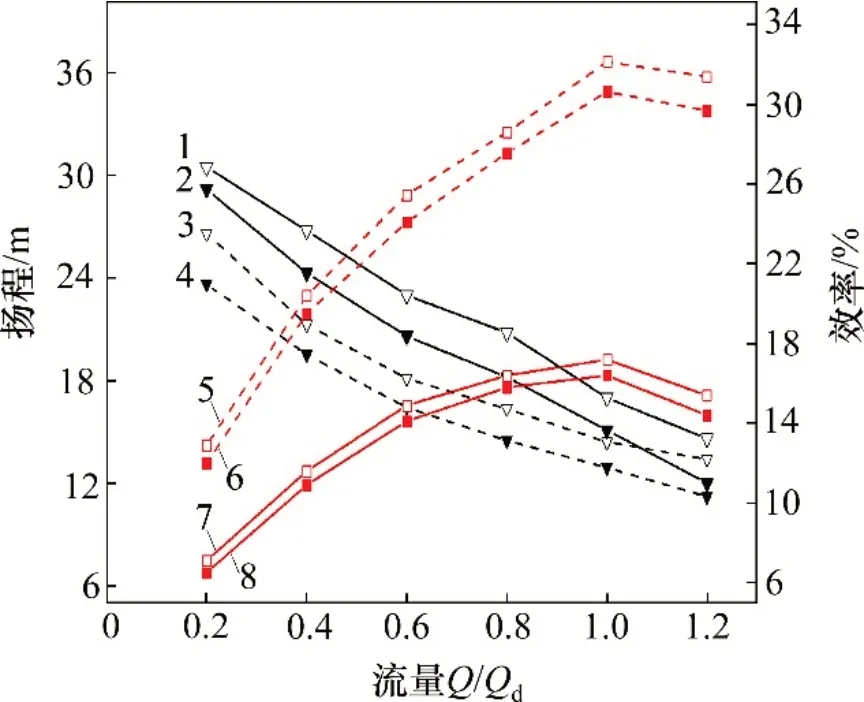
图6 模型泵外特性曲线Fig.6 The pump characteristic curve

从图6可见：优化后模型在各个工况点的效率较原模型都提高，在额定工况下，原模型试验效率为16.4%，优化模型试验效率为17.2%，泵效率提高了0.8%；对比模拟结果与试验结果，额定流量点附近效率变化误差小于3%，大流量工况下误差小于5%。图6中试验的泵效率是低于数值计算的泵效率，这是由于数值计算未考虑容积损失与机械摩擦损失。由此验证了本文采用的网格及模型能够较准确地预测该泵扬程的变化与效率的变化，为数值计算的准确性提供保证。

3.2 内流计算

图7所示是设计工况下模型泵优化前后射流器以及叶轮内流湍动能云图。由射流器内部湍动能可知，高湍动能区域往往出现在喉管进口与喉管出口处，而原模型喉管内部湍动能分布规律与优化模型是一致的，原模型内部湍动能稍大，由此说明原模型在喉管处能量耗散相对较大。而由图7中叶轮处湍动能分布可得，湍动能峰值出现在叶轮进口处，叶轮进口是能量耗散较大的区域，对比2个叶轮内湍动能分布，原模型整个叶轮流道湍动能分布不均匀，其与优化模型相比也存在较大的湍动能损失，从而使射流泵的效率受到影响。优化模型由于能量损失小，因此，射流泵的效率得到提高。

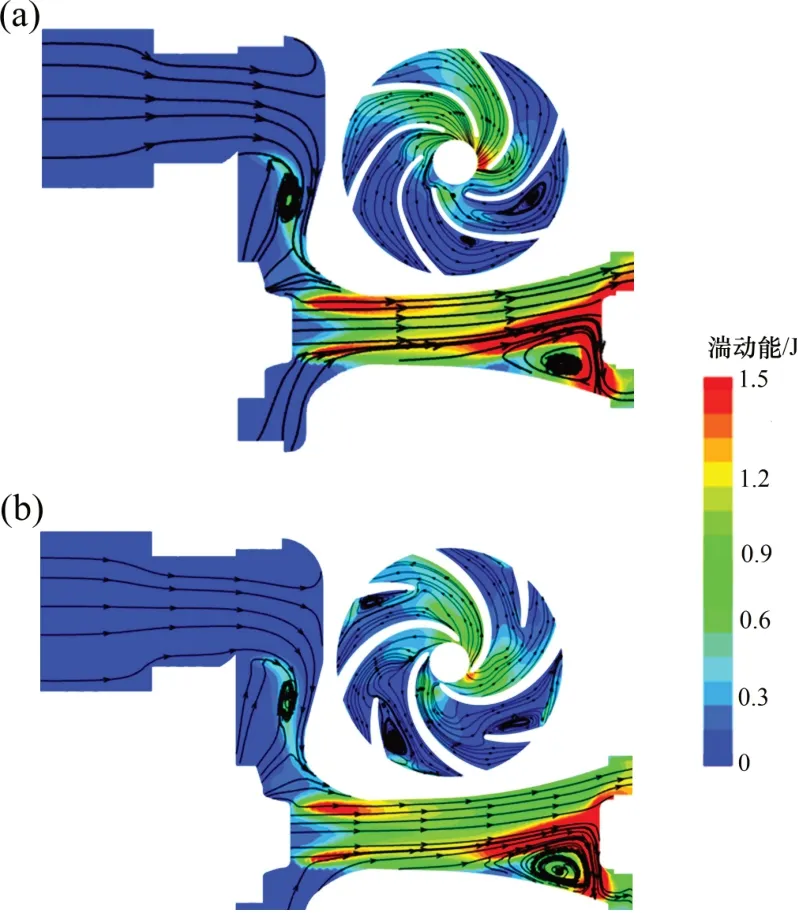
图7 模型泵射流器叶轮内流湍动能云图Fig.7 Turbulent kinetic energy cloud diagram of jet and impeller

由图7可见：优化前后射流器部分流体流态相似，且出现的涡流都在同一区域，涡流最大区域出现在射流器下游靠近出口处。产生这种现象的原因是流体经过喉管时，因喉管内部与外部存在压差从而产生射流，射流的作用将流体高速推射出喉管，由于结构与流体的碰撞进而在出口处形成高速回流。而对于优化前后叶轮处流体流线，原模型出现涡流区域在长叶片的工作面进口稍后区域，而优化模型出现涡流的区域在短叶片背面进口靠后区域。

图8所示为模型泵优化前后导叶内部流体的压力云图。由图8可知：模型泵优化前后导叶处的流态相似，无明显变化，且无明显的漩涡区域；导叶处压力较大的区域往往是在A区与导叶叶片出口处。对比可得，优化后A区处压力较原模型更加均匀。但在导叶出口发现优化后模型的压力明显大于原模型的压力，这说明经过优化后的叶片在相同条件下较原叶片做功更大。

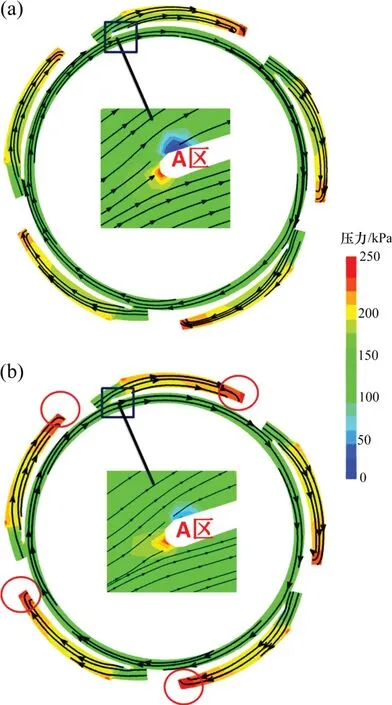
图8 模型泵导叶内流压力云图Fig.8 Pressure cloud diagram of guide vane of model pump

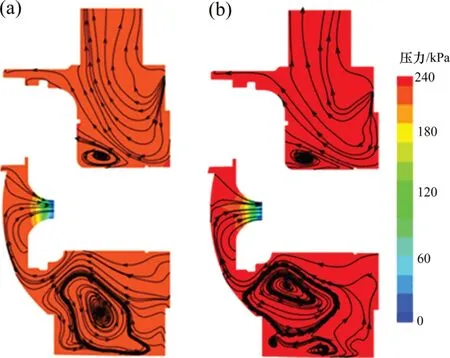
图9 模型泵腔体内流压力云图Fig.9 Pressure cloud diagram of cavity of model pump

图9所示为模型泵优化前后腔体内流压力云图。由图9可知：优化后腔体内压力整体比原模型的大，而腔体中压力陡变出现在腔体与射流器的交界处，而此处出现压力陡变的原因是腔体内压力与射流其内部压力存在很大的压差，从而使得流体由腔体进入射流器的喉管时产生射流作用。由图9可以看出腔体内产生涡流的区域往往出现在腔体的下游区域，这是因为此区域靠近射流器部件，导致流体流经此处时流速陡然上升，从而出现流态紊乱。对比优化前后模型可知腔体内流线规律是一致的，但优化模型在腔体下游漩涡区域较原模型更小，因此，优化模型较原模型腔体内流态较好。

3.3 内场噪声计算结果及试验验证

模型泵定子部件包括泵体、导叶以及射流器，转子部件为叶轮。由于转子部件和定子部件所诱发的内场流体动力噪声计算方法不同，故需要分别求解。图10所示为模型泵各部件声源频谱分布。从图10(a)可见：原模型泵内导叶部件贡献的噪声最大，而与定子部件相比叶片处贡献噪声相对较小，可以忽略其对泵体整体噪声的影响。泵体噪声往往在叶频(叶片通过频率)及其倍频处出现幅值，原模型定子部件与转子部件的噪声在2倍叶频(550 Hz)之前相对较高，2倍叶频后趋于平稳，而由图10(a)可以看出定子部件主要出现了5个比较明显的峰值，而这些峰值都出现在叶片通过频率处，由此可以得出叶频是影响射流泵噪声的主要因素。所以，降低叶频干扰因素是降低射流泵内场噪声的最有效的方法。

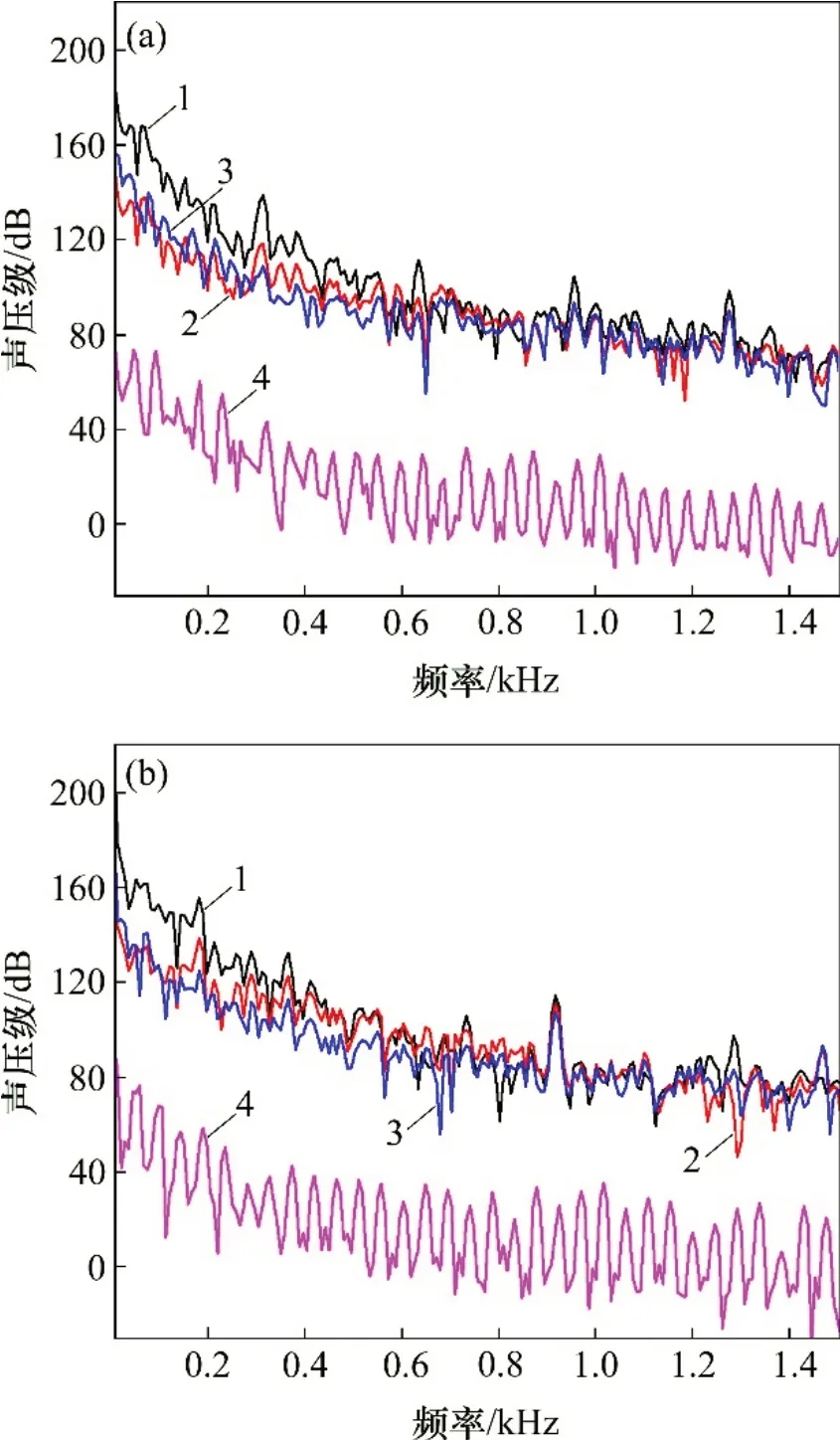
图10 模型泵各部件声源频谱分布Fig.10 Components sound spectrum distribution of model pump

由图10(b)可见：优化后泵内导叶部件仍然是贡献噪声最大部件，而叶片依旧是贡献噪声最小的部件。对比图10(a)可见：加入短叶片后明显改善了叶频对噪声的影响，在整个噪声频带上都比较平稳，图中只有1 处明显峰值，出现在916 Hz 处，此时导叶处噪声数值为114 dB，腔体处噪声数值为111 dB，射流器处噪声数值为107 dB。而在原模型中各个叶频处各定子部件噪声均值在110 dB 以上，且原模型主要噪声集中在1倍叶频(275 Hz)之前以及各倍叶频处，而优化模型主要噪声集中在1 倍叶频(375 Hz)之前，在整个宽频带上声压级比较平稳，很好地降低了原模型在各个叶频处的声压级。对比各个部件内场噪声声源进出场点频响曲线可以看出模型泵噪声主要集中在导叶部分，其次是腔体，最后是射流器，为了更加清楚地了解各部件对泵体所贡献噪声的具体情况，需要通过公式(1)计算得出各部件所产生的总声压级。表2所示为泵体不同部件内声场总声压级对比表。

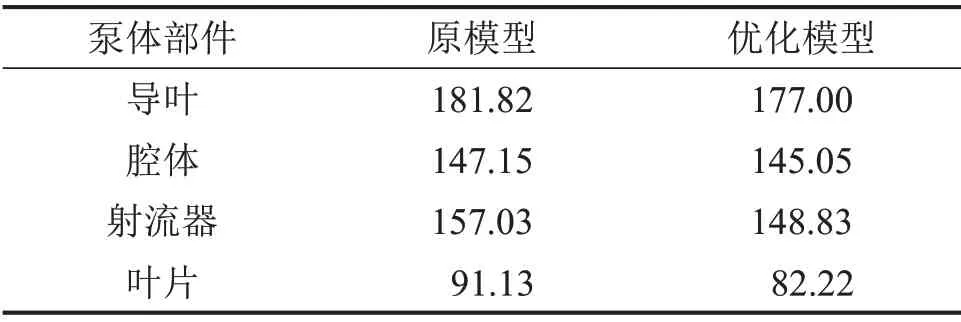
表2 泵体不同部件内声场总声压级对比Table1 Comparison of total sound pressure levels of pump internal sound field in different parts of pump body dB

由表2可知：优化模型与原模型相比，各个部件的噪声贡献都降低，尤其是射流器部分降低最为明显，总声压级下降8.2 dB；腔体部分声压级降幅较小，优化后降低2 dB 左右；导叶部分也下降4.8 dB。而根据式(1)可以知道，泵体内部总声压级降低4.8 dB左右。本文还通过试验进行对比验证，从而进一步说明计算结果的准确性与理论推论的正确性。本文模拟结果如下：原模型泵体内部总声压级为178.82 dB，优化模型泵体内部总声压级为174 dB。试验结果如下：原模型泵体内部总声压级为186.62 dB，优化模型泵体内部总声压级为183.6 dB，可见数值计算结果与实验结果相对误差小于5%，文中所述数值计算方法具有较高的精度。通过上述数据可以得出声压模拟结果比试验结果小，这是因为数值模拟时未考虑实际情况下的声固耦合作用。

3.4 外场噪声计算结果

在进行外声场模拟计算前，先计算模型泵的结构模态。由于模型泵的泵体和支架、管道是连为一体的，但其材质不同，所以，在建模过程中需要分别定义材料属性，模拟中为降低问题的复杂性，忽略小尺寸的结构。图11所示为射流自吸泵体结构三维图。

图11 射流自吸泵体结构三维图Fig.11 3-dimensional diagram of structure of jet self-priming pump body

为分析不同定子部件作用下对模型泵的外场流动噪声的影响，选取不同定子部件下指向性场点声压数据进行分析。图12所示为模型泵不同定子部件作用下的流动辐射噪声声压指向性分布。

由图12可知：原模型3个定子部件所诱发的辐射噪声在轴频(APF)时辐射最广，在各个方向均起主要作用，而在优化模型中这种现象有所变化。优化模型外场流动噪声在3倍轴频(3APF)时平均辐射最广，这种情况在导叶部件最为明显。由原模型泵腔体部件的外场流动噪声声压分布规律可知。前3倍轴频声压分布规律相似，对比优化模型可知优化模型腔体也满足这种规律，且优化模型前3倍轴频外场流动噪声辐射范围基本持平。对比原模型，优化模型在各轴频叶频下噪声辐射范围普遍小。为了更直观地对比模型降低的外场噪声效果，用各部件声压曲线来进行对比，并通过计算得到优化前后泵体外场总声压。

图13所示为模型泵不同定子部件声源作用下的外场辐射声压级频率曲线。从图13(a)可见：对泵整体外场噪声影响最大的是导叶部分，其整个宽频声压一直较高，并无明显下降趋势，且在3 倍叶频(825 Hz)处出现峰值，此时声压为100 dB。而腔体与射流器部分声压随着频率增加有下降的趋势，射流器部分下降更为明显，与泵中各个定子部件相比，射流器部分对整个泵体的外场声压贡献最小。从图13(b)可见：优化后，对泵整体外场噪声影响最大的仍然是导叶部分，但其整体声压与原模型相比有了明显降低，而射流器部分的声压对整个泵体的外场声压贡献仍然最小。优化模型各定子部件在900～1 000 Hz都出现了峰值，且出现峰值的频率很接近，说明在这个频率下泵体内产生的能量还是很大。与原模型相比，优化模型在各个定子部件在整个宽频带上都降低。本文通过总声压级的概念来论证结果的可行性，表3所示为泵体不同部件外声场总声压级对比表。

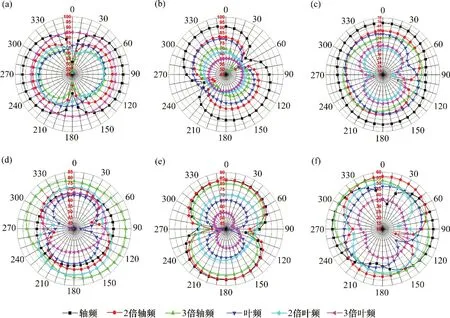
图12 模型泵流动辐射噪声声压指向性分布Fig.12 Directivity distribution of acoustic pressure of flow radiation noise of model pump optimization

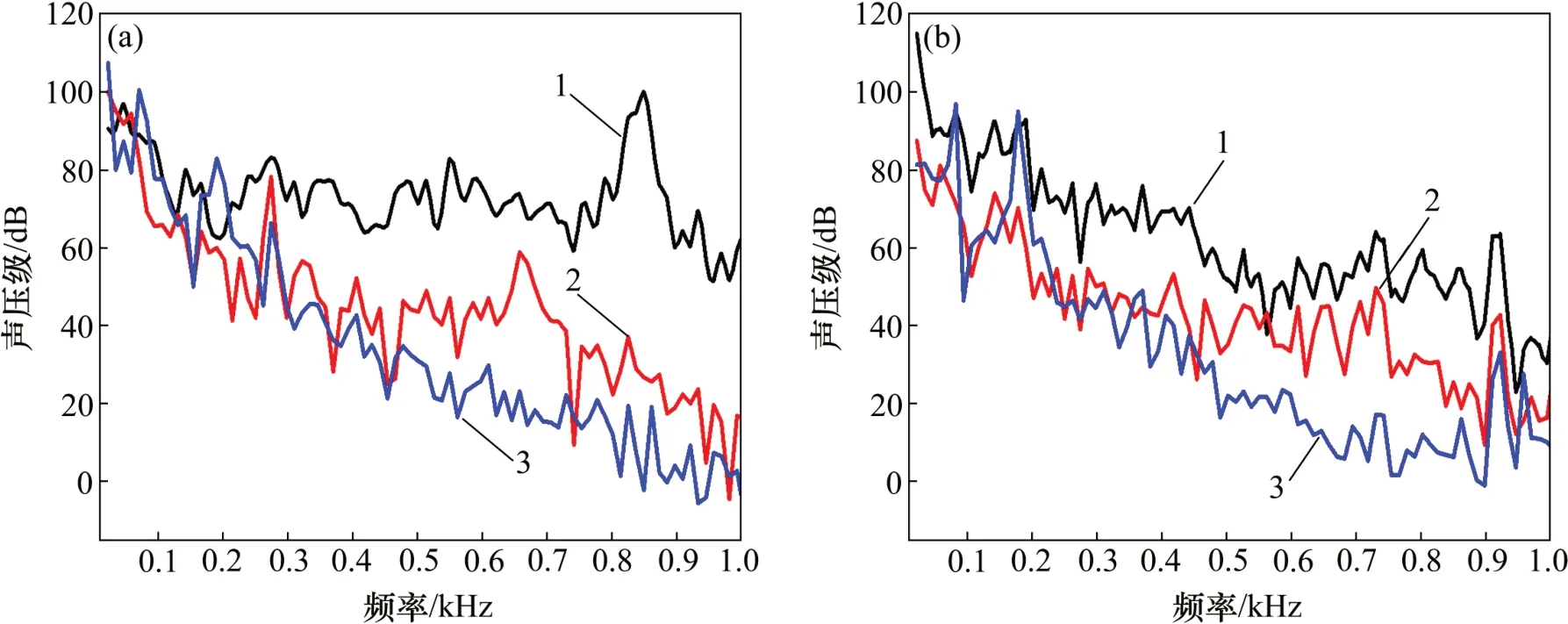
图13 模型泵不同定子部件声源作用下的辐射声功率频率曲线Fig.13 Radiated sound power frequency curves of different stator components of model pump optimization

由表3可知：优化模型与原模型相比，各个部件的外声场辐射声压级都降低；而与原模型整体外声场辐射声压级相比，优化模型降低了2%。

表3 泵体不同部件外声场辐射总声压级对比表Table1 Comparison of total sound pressure levels of pump external sound field in different parts of pump body dB

4 结论

1)优化叶片后泵模型与原叶片泵模型相比在各个工况下扬程与效率都有了显著提高。在额定工况下，扬程提高12.6%，效率提高0.8%。

2)泵优化前后导叶偶极子声源诱发的水动力噪声对内场噪声贡献最大，起主要作用。而叶片扇声源诱导的水动力噪声对内场噪声贡献最小。

3)叶片通过频率是影响泵噪声的主要因素，优化模型有效降低了叶频处的声压级峰值。

4)模型泵优化后泵体内场噪声降低1.6%，外场噪声降低2%，且与原模型相比，各个部件产生的噪声都有所降低。