深埋隧洞三岔口围岩稳定性计算理论
饶军应,谢财进,赵霞,刘灯凯,聂崇欣,刘宁
(贵州大学土木工程学院,贵州贵阳,550025)
随着我国交通行业飞速发展,隧洞建设规模越来越大,隧洞也越修越长,对技术的要求越来越高。为满足隧洞工期及运营通风需求,需要增设斜井、横通道等辅助坑道,而辅洞与主洞连接处会形成三岔口。从力学角度分析,隧洞主洞的围岩受力通常可视为平面进行求解,当存在辅助坑道介入主洞时,三岔口区的围岩受力将变得十分复杂,该区域内的开挖易造成隧洞围岩的受力状态由最初的三向受力转变为开挖后的单向或二向受力,且应力分布也截然不同,若未探明三岔口区围岩应力的分布情况,贸然掘进会增加施工风险。三岔口区围岩极易松动、掉块或坍塌,是隧洞开挖时的薄弱点,需予以特别关注,为此,有必要研究三岔口处围岩受力分布[1-3]。近年来,学者们就隧洞三岔口处围岩稳定性开展大量研究,基于已有文献可知,主要有数值分析和应用研究2 个大类[4-12]。在数值分析方面,罗彦斌等[13]通过现场实测和有限元数值模拟,研究了横通道斜交隧洞对主隧洞结构受力及变形的影响,但未涉及理论解析;蔺云红等[14]研究了地铁暗挖隧洞斜交下穿既有铁路工程时的地层沉降和塑性区分布,仍依靠数值模拟分析,未涉及理论解析。在应用研究方面,李东海等[15]结合工程实例,对盾构隧洞斜交下穿地铁车站的施工进行了分析,仅依靠监测数据和工程经验给出施工指导意见,未给出理论解释。已有研究成果表明:新建隧洞三岔口区设计、施工的主要依据源于类似工程的数值模拟、施工参数及工程经验,在理论解析层面还有待加深。本文基于辅助坑道连接隧洞主洞,对其三岔口区围岩稳定性进行理论探讨,以便为类似工程的设计、施工提供理论支撑。
1 隧洞三岔口围岩应力分析
隧洞开挖后,围岩应力将重新分布,局部可能出现应力集中,导致变形甚至失稳破坏。图1所示为隧洞三岔口受力计算分析图。分析图1可知:辅洞与隧洞主洞相交成锐角一侧(定义为三角区)受力面积小,该区域受应力集中破坏可能性最大。为计算简便,假设隧洞主洞、辅洞为不同直径的圆形隧洞,且为深埋隧洞(围岩应力计算时仅考虑岩体容重与隧道埋深),此时,隧洞边界岩体所受应力简化为垂直应力P(P=γH,γ为岩体容重,H为隧洞埋深)和水平应力q(q=λP,λ是侧压力系数),忽略围岩自重的影响。
按弹性理论中的基尔希公式建立如图2所示的计算模型,计算围岩中任一点Q(ρ,θ)的应力[16]:


图1 隧洞三岔口受力计算分析图Fig.1 Analysis of force calculation of the tunnel three mouths

图2 隧洞围岩应力分布范围及计算简图Fig.2 Stress distribution range and calculation sketch of tunnel surrounding rock
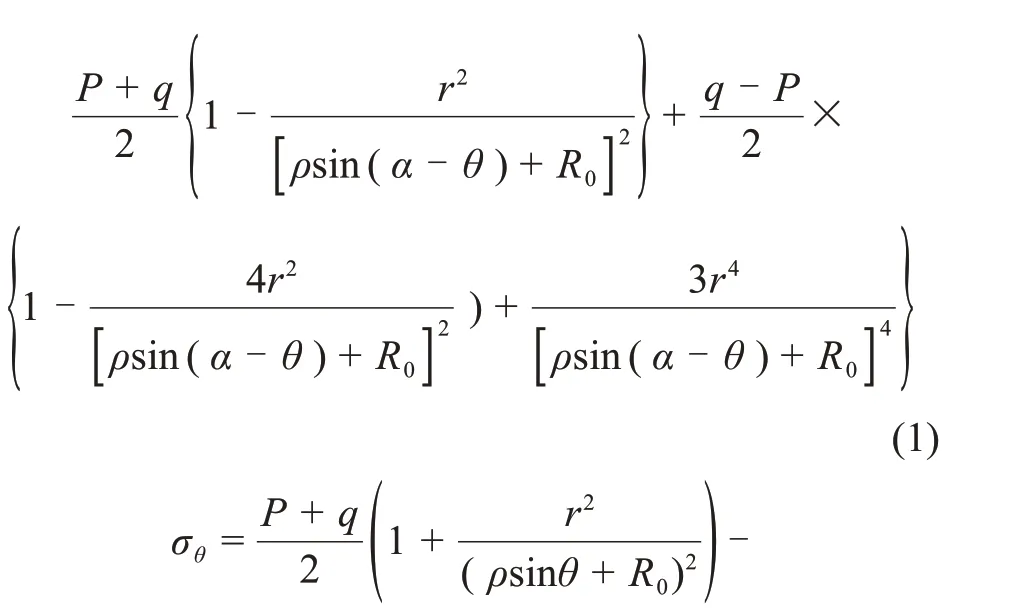

式中:σρ为沿ρ方向的正应力;σθ为沿θ方向的正应力;τρθ为切应力;R0为隧洞三岔口中心至塑性变形圈边界的距离;r为隧洞主洞开挖半径;ρ和θ为某点应力的极坐标;α为辅洞与隧洞主洞的交叉角度(锐角)。
根据隧洞三角区域围岩力学特征及圆形隧洞弹性状态下围岩应力计算公式[17],可得隧洞三角区围岩垂直应力σh为
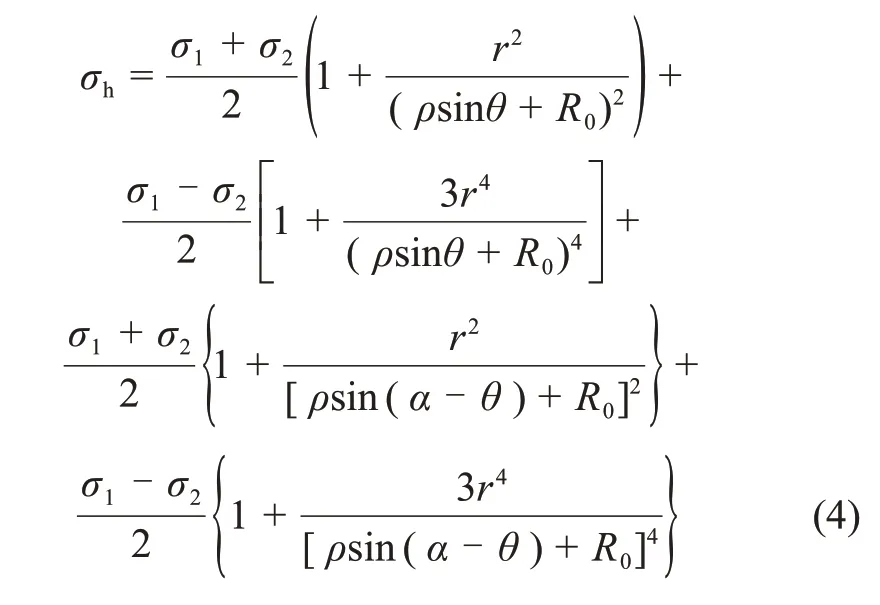
式中:σ1和σ2分别为原岩垂直应力和水平应力,且σ1=P,σ2=q=λP。
将σ1和σ2代入式(4),可得

简化为
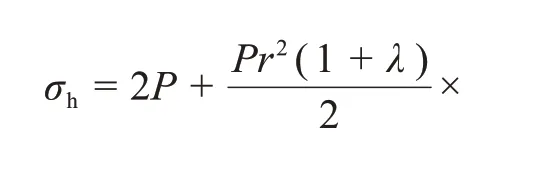

要计算σh,还需求解未知量R0,由卡斯特纳(Kastner)公式得:

式中:ξ为摩尔圆强度线的斜率;σc为岩石抗压强度。
由摩尔-库仑强度理论得:

经简化得

由 于σ1=ξσ3+σc,可 得:(其中:c和ϕ分别为岩体粘聚力和内摩擦角)。
将σc代入式(7)得

随着隧洞的开挖,其三角区围岩应力将重新分布,并伴随应力集中现象的产生,该区域应力集中的强弱用系数K表示。

由式(11)可知,三角区围岩应力与原岩应力、围岩自身强度、岩体侧压力系数、隧洞截面形状、尺寸及辅洞与隧洞主洞的交叉角度有关。
2 三岔口围岩破坏规律分析
2.1 三岔口围岩破坏深度分析
图3所示为围岩状态分布图。隧洞三角区围岩应力集中系数较高,当集中应力大于岩体极限屈服强度时,围岩由于支撑力不足发生塑性屈服破坏。随破坏区的扩散,围岩周围将依次形成松动区、破碎区、破裂区、塑性区、弹性区和原岩区。图4所示为弹塑性区围岩应力分布特征图。由图4可见:若集中应力未超过岩体极限屈服强度,可认为围岩处于极限应力平衡状态。根据弹塑性区围岩应力分布,由弹塑性极限平衡理论可知:

图3 围岩状态分布图Fig.3 Distribution of surrounding rock state

图4 弹塑性区围岩应力分布特征图Fig.4 Stress distribution of surrounding rock in elastoplastic zone
弹性区围岩应力可描述为[18-19]:
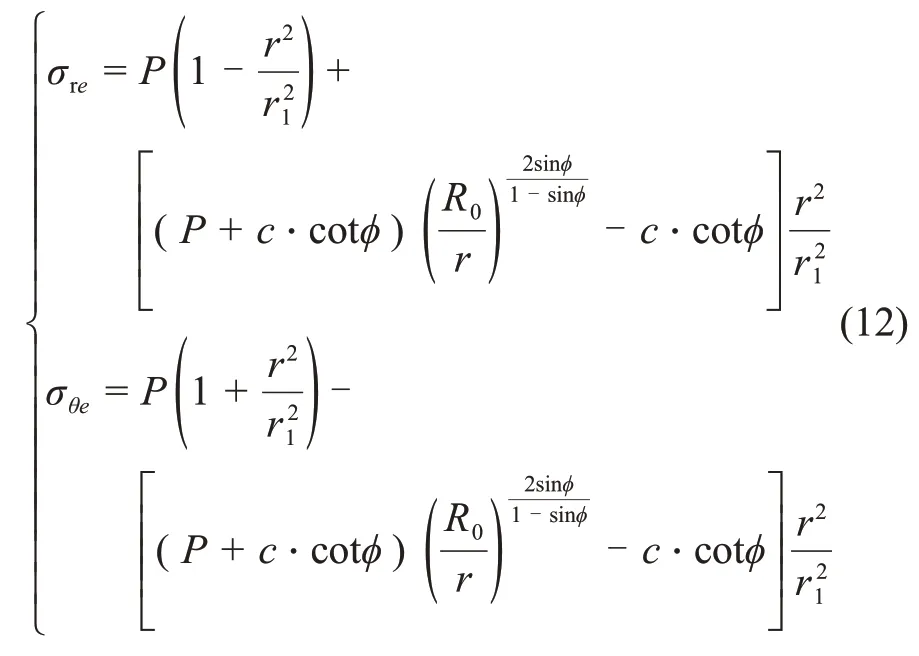
式中:σre为弹性区径向应力;σθe为弹性区环向应力;r1为松动圈半径,
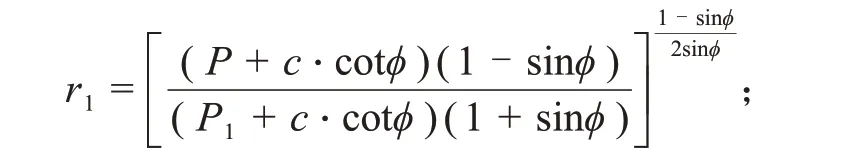
P1为支架反力。
结合式(12),可知三角区应力叠加后弹性区内沿水平方向的铅垂应力σx和沿铅垂方向的水平应力σy为:

式中:x和y为辅洞与主洞的掘进距离;r′为斜井开挖半径。
塑性区围岩应力可描述为[18-19]:

式中:σrP为塑性区径向应力;σθP为塑性区环向应力。
结合式(14),可知三角区应力叠加后塑性区内沿水平方向的铅垂应力σx和沿铅垂方向的水平应力σy为:
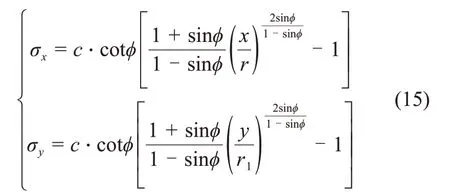
联立式(13)和(15)解得三角区围岩水平方向和铅垂方向的破坏深度为:

式中:Xmax和Ymax分别为三角区围岩水平方向和铅垂方向的破坏深度。
图5所示为三角区围岩应力分布及破坏范围分布图。由图5可见:沿x方向的三角区最大破坏深度为Xmax,沿y方向的三角区最大破坏深度为Ymax。
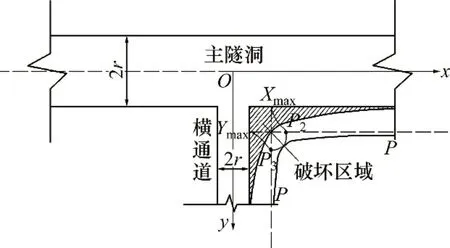
图5 三角区围岩应力分布及破坏范围分布图Fig.5 Stress distribution and damage range of surrounding rock in triangle area
水平方向铅垂应力的峰值位于x=Xmax处,为P3;铅垂方向水平应力的峰值位于y=Ymax处,为P2。2 条应力曲线的交汇处围岩应力集中系数最大,由数学关系可知围岩最大破坏深度Q为
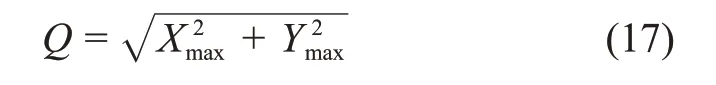
将式(16)代入式(17)得:
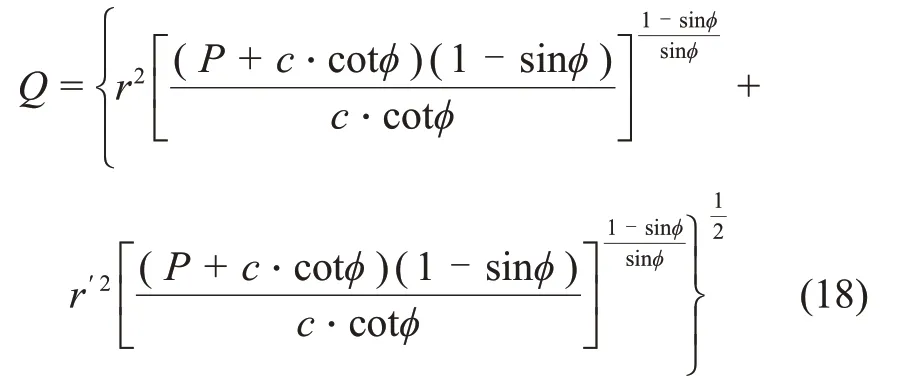
由于应力叠加的作用导致三岔口处形成曲边三角形破坏区,其最大破坏深度与隧洞、辅洞开挖尺寸、原岩应力、岩体自身强度以及辅洞与主洞交角有关。若辅洞进主洞的开挖过度曲线在破坏区域内,则三岔口区围岩不稳定,需进行加固;反之,三岔口区围岩稳定。
2.2 三岔口围岩等效跨度分析
图6所示为围岩压力变化特征曲线。由图6可见:根据围岩变形特征分为弹塑性阶段(AB段)、小松动变形阶段(BC段)、大松动变形阶段(CD段)。隧洞三岔口围岩由于二次开挖导致应力集中,当集中应力大于围岩极限强度时,围岩将发生塑性屈服破坏,失去支承能力。在无支护条件下,隧洞顶板将会进入小变形阶段甚至大变形失稳破坏阶段,主要表现在较软弱岩层中顶板冒落及隧洞两帮支撑力不足时顶板弯曲下沉[20-24]。
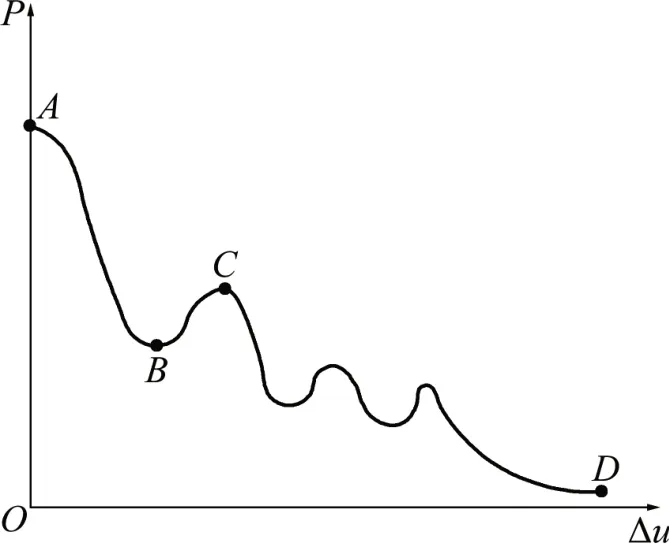
图6 围岩压力变化特征曲线Fig.6 Curve of variation of surrounding rock pressure
图7所示为隧洞三岔口区跨度示意图。由图7可见:顶板弯曲下沉时,基于隧洞三岔口围岩破坏形式及特征,采用等效跨度理论计算该区域理论最大等效跨度Ltmax和极限等效跨度Lpmax[25]。

图7 隧洞三岔口区跨度示意图Fig.7 Schematic diagram of span of the tunnel
由隧洞三岔口处的几何关系可得
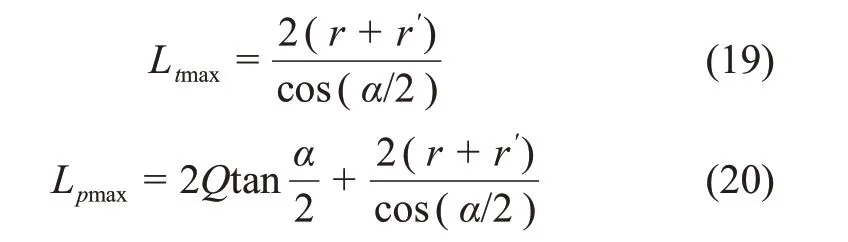
将式(18)代入式(20)可得:

等效跨度值作为隧洞三岔口区围岩变形位移参数,可反映围岩稳定性。该值不仅受交叉角α、隧洞尺寸r和r′及破坏深度Q的影响,而且与隧洞埋深H、围岩力学参数等有关。通过研究发现:当实际修建跨度值L不大于Ltmax时,即L≤Ltmax,三角区围岩稳定;当遇特殊地质条件时,L会超出Ltmax,但不大于Ltmax,即Ltmax≤L≤Lpmax,此时,需对三角区围岩进行适当加固;若L≥Lpmax,则三角区围岩极不稳定,需采取有效加固措施。
3 算例与分析
以贵阳市轨道交通2号线区间为例,全区间采用矿山法,隧洞为双洞单线马蹄形断面结构,采用复合式衬砌,最大埋深53.2 m。为计算简便,取岩体容重γ=19 kN/m3,隧洞埋深H=50 m,将该隧洞主洞、辅洞分别假定为半径r=5.0 m,r′= 4.0 m的圆形隧洞。
3.1 隧洞三角区垂直应力分析
1)当R0→∞,得

隧洞三角区围岩垂直应力仅与隧洞上部岩体容重及隧洞埋深有关。
2)当R0为5r,4r,3r和2r时,分别得式(23),(24),(25)和(26):
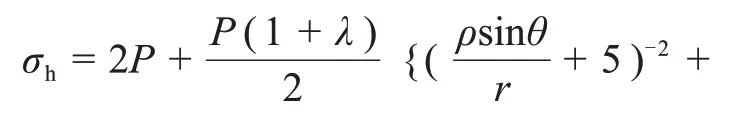


图8 不同R0下三角区垂直应力分布Fig.8 Vertical stress distribution of lower triangular region in different R0
取侧压力系数λ=0.5,α分别为30°,45°,60°和90°时,由式(22)~(26)分别得σh的分布曲线。图8所示为不同塑性圈下三角区垂直应力分布图。由图8可见:随着X逐渐减小,围岩所受垂直应力也逐渐减小;随着α逐渐减小,三角区两侧的围岩应力差值变小,隧道结构更稳定;当α=30°时,三角区所受峰值应力最小,且两侧围岩垂直应力差值最小,三角区围岩较为稳定,开挖条件较好;当α=90°时,三角区所受峰值应力最大,且两侧围岩垂直应力差值最大,三角区围岩极不稳定,此种开挖方案安全风险极高;随着R0减小,σh逐渐增大,且三角区两侧σh差值逐渐增大,不利于隧道稳定。故需通过围岩力学参数确定塑性圈范围,根据垂直应力对隧洞三岔口区进行合理加固与开挖。
为进一步验证本文理论解析的可行性,现用ANSYS有限元软件对辅洞与主洞交叉角呈45°时的算例进行数值模拟计算,其网格划分如图10所示。
取α=45°,λ=0.5,三岔口区处于Ⅲ级围岩中,数值模拟结果、解析计算结果如表1所示。由表1可见:1)解析计算和数值计算三岔口区围岩垂直应力最大值间存在的最大误差仅为3.92%;2)在同种工况下2种计算方法的结果存在微小误差,原因在于理论解计算结果为确定值,而数值解则是近似运算的结果,且2种方法的计算假定条件存在差异;3)理论解与数值解间的计算结果十分接近,验证了本文解析法在三岔口区围岩稳定性计算中的可行性和准确性。
3.2 隧洞三角区应力集中分析
图11所示为三岔口应力集中系数等值线分布图。由图11可见:越靠近围岩三岔口交叉点,围岩应力集中系数越大,三角区域最外围的应力集中系数最小。这是由于隧洞开挖过程中三角区域外围岩体容易破坏,在其表面形成卸压区,为给横通道与主洞交叉处的顶板提供足够支撑力,有效支撑区将会向岩体深部转移,故而应力集中减弱。在实际工程中,一般会将辅洞与隧洞主洞交叉处的尖角部分去掉修建成曲线状,该过渡曲线应不越过K等值曲线,且与其弯曲程度相似,最好与等值曲线重合。
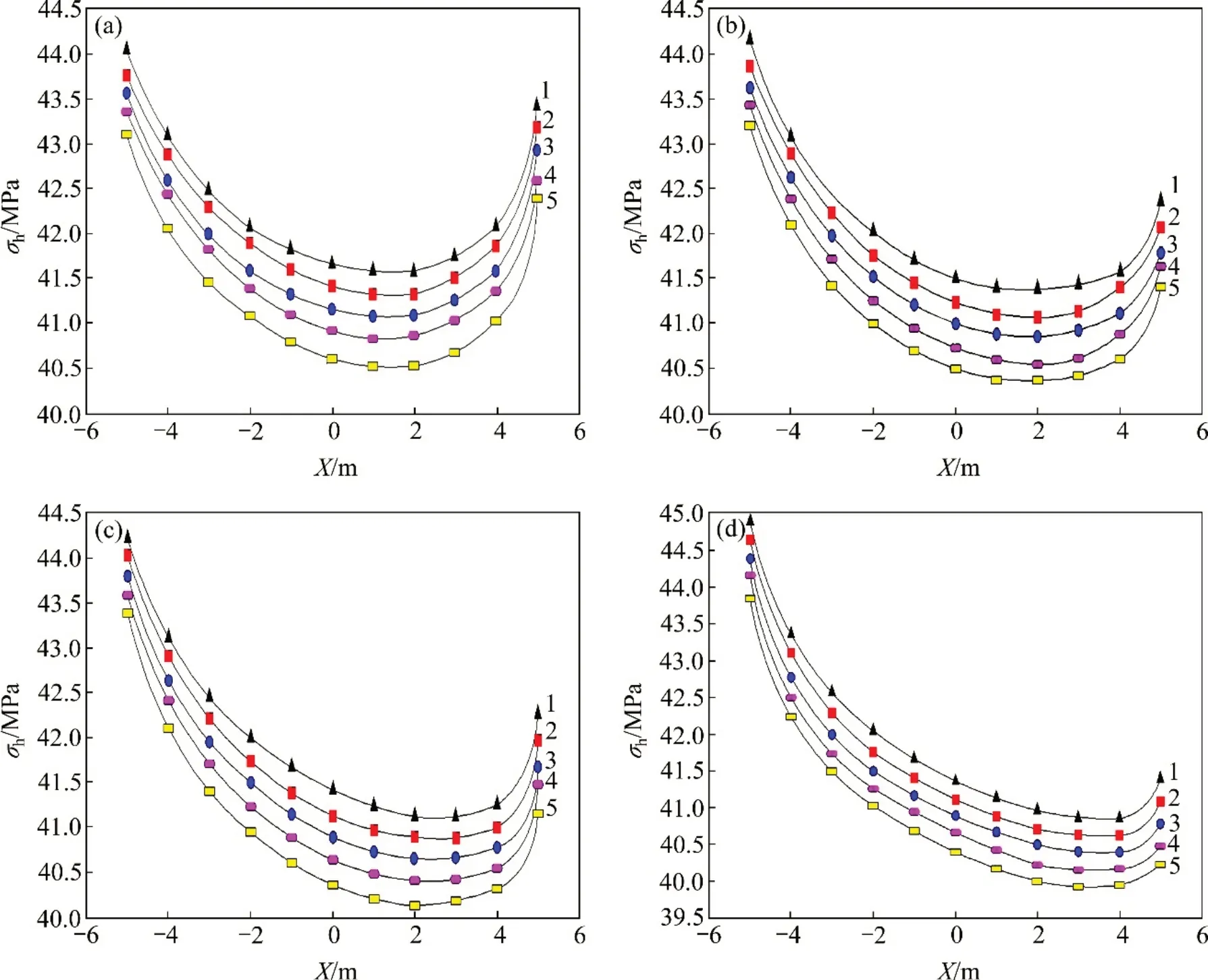
图9 不同α下三角区垂直应力分布图Fig.9 Vertical stress distribution in different α lower triangular region

图10 ANSYS有限元计算网格划分图Fig.10 ANSYS finite element calculation grid division diagram
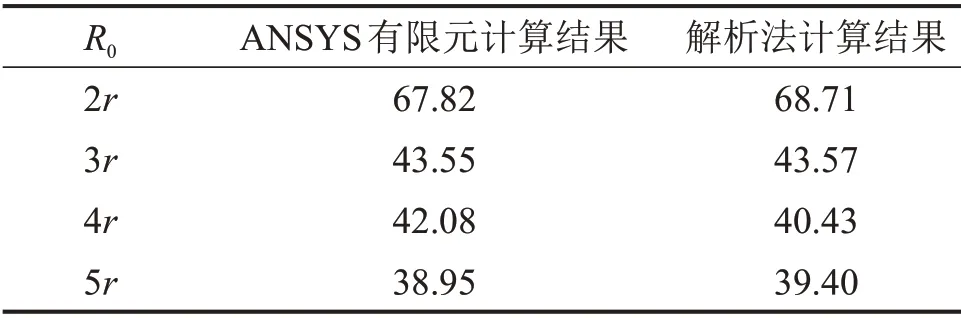
表1 辅洞与主洞夹角为45°三岔口区围岩垂直应力最大值Table1 Maximum value of vertical stress of surrounding rock in divergence area when the angle between the auxiliary hole and the main hole is 45° /MPa

图11 三岔口应力集中系数等值线分布图Fig.11 Contour map of stress concentration factor of divergence
由式(11)可知:影响应力集中系数的主要因素有λ,r,R0及α。其中λ和R0是由隧洞所处地理位置决定,针对不同用途r也有相应固定标准,在实际工程中,α的随机性较大。
当λ取0.5,R0取3r,r取5 m,代入式(11)后得:


由式(27)绘制不同α下的K曲线,如图12所示。由图12可见:随着α的增大,K的峰值逐渐变大,当α=90°时,K的峰值最大。此时三角区应力高度集中,围岩稳定性差,不宜于开挖。故而辅助坑道进入隧洞时需以一定角度进入,避免正交方式。

图12 应力集中系数曲线图Fig.12 Curves of stress concentration factor
3.3 隧洞三角区破坏深度分析
表2所示为不同围岩级别下摩擦角φ和黏聚力c。随着围岩等级降低,岩体摩擦角φ和黏聚力c逐渐减小。不同等级围岩过渡转换时,可根据隧洞三角区最大破坏深度理论计算值,对其加固进行合理化建议。
由式(18)可计算不同围岩级别下隧洞三角区最大破坏深度。图13所示为围岩破坏深度曲线图。由图13可见:随着围岩等级降低,破坏深度逐渐增加,Ⅰ至Ⅳ级围岩三角区破坏深度递增趋势不明显,Ⅴ级围岩中破坏深度层指数形式增加,围岩级别越差,三角区破坏深度越深。另外,在围岩等级过渡段,其破坏深度会发生突变,故在围岩不均匀地段开挖时,需考虑应力突变的状况;在围岩过渡段设计、施工时,需设置一定的安全系数。
3.4 隧洞三角区等效跨度分析
图14(a)所示是由式(19)绘制的α与Ltmax的关系曲线。由图14(a)可见:随α增大,Ltmax单调递增,当α=90°时,Ltmax达到最大值,Ltmax曲线下方为隧洞开挖安全区。
太湖新城地下空间工程位于太湖新城核心启动区地下,项目总建筑面积30万m2,占地面积6.8万m2,地下共3层,结合地铁4号线支线溪霞路站沿中轴大道南北向布置。地下1层为商业及公共配套设施,设置大量下沉式广场,进行地面地下交通转换。地下2层和3层为公共停车空间,共20万m2,可容纳停车2 800辆。该项目计划于2013年12月开工建设。
令最大破坏深度Q=5 m,图14(b)所示是由式(20)绘制的α与Lpmax关系曲线。由图14(b)可见:随α增大,Lpmax单调递增,当α=90°时,Lpmax达到最大值。当遇特殊情况时,开挖等效跨度可适当增加,但也不能超过Lpmax曲线的范围。Ltmax曲线下方为开挖安全区,Lpmax曲线与Ltmax曲线之间为开挖极限区。
当辅洞与隧洞主洞交角α=90°时,得:
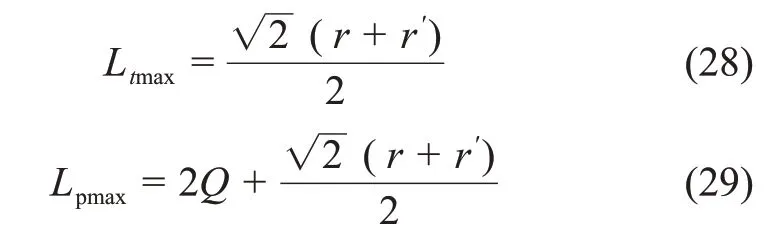
将式(18)代入式(29)得:


图14 交叉角(α)与等效跨度的关系曲线Fig.14 Cross angle(α)and equivalent span relationship curve
由式(19)和(20)可知,当辅洞与隧洞主洞交角一定时,理论最大等效跨度仅与隧洞尺寸有关,极限等效跨度还与最大破坏深度有关。在设计辅洞进入主洞区时,实际修建跨度应小于理论最大等效跨度,在特殊条件下也不能大于极限等效跨度。
4 结论
1)当α=90°时,围岩垂直应力最大,随着α和λ减小,σh减小;随着R0减小,σh逐渐增大。已知围岩力学参数、地勘参数,就可根据理论公式对隧洞三岔口区围岩进行合理加固。
2)在隧洞开挖过程中,越靠近围岩三岔口的交叉点K越大,三角区域最外围的K最小,且随着α的增大,K逐渐变大,当α=90°时,K达到最大值。
3)随着围岩等级的降低,破坏深度越大,Ⅰ~Ⅳ级围岩三角区破坏深度递增趋势不明显,Ⅴ级围岩中破坏深度呈指数形式增加。
4)隧洞三角区的集中应力大于围岩极限强度时,围岩会发生塑性屈服破坏,失去支承能力,在无支护条件下隧洞顶板将会进入小变形阶段,甚至进入大变形失稳破坏阶段。
5)当α一定时,Ltmax仅与隧洞尺寸有关,Lpmax还与最大破坏深度有关。在设计辅洞进入主洞区时,L应小于Ltmax,在特殊条件下也不能大于Lpmax。

