三场耦合作用下黏土岩损伤变形特性及本构模型
(四川农业大学 土木工程学院,成都 611830)
1 研究背景
在岩土工程领域经常涉及多场耦合问题,特别是对于处在深部地下的工程,例如垃圾填埋工程、矿井工程、高放核废物处置工程等[1-3]。二十世纪六七十年代以来,岩体的THM(温度-渗流-应力场)耦合问题便成为岩土工程界的热点讨论话题,众多的专家学者都致力于分析岩体在三场耦合作用下的力学损伤行为,并已取得了一定的研究成果。
黏土岩是高放处置库常用的一类地质屏障材料,由于地下水及核素释放热量的影响,周围岩体会经常处于温度场、渗流场以及应力场的三场耦合作用,研究黏土岩在THM耦合作用下的变形损伤演化过程关系到处置库安全的重要议题[4]。垃圾填埋场也存在上述问题,垃圾产生生物化学作用并释放大量的热量和气体,对垃圾处理场黏土覆盖层的渗流特性、变形特性、强度特征以及热传导性等都会产生不同程度的影响,从而影响垃圾填埋场长期稳定运行[5]。众多研究表明:温度对黏土岩的变形特性具有重要影响,黏土岩的强度随着温度升高会逐渐降低,蠕变变形速率则会明显加快[6-7]。龚哲[8]通过开展THM耦合条件的固结不排水三轴压缩试验和排水三轴蠕变试验研究,建立了黏土岩相应的三场耦合损伤蠕变本构模型。
本文在总结前人研究经验和理论基础的前提上,开展了25,50,75,100 ℃ 4种温度下的三轴压缩渗透试验研究,重点研究了温度、变形损伤以及渗流特性三者之间的相互关系。
2 试验概况
国内某高放储气库埋深300 m处,含有一段泥岩、黏土岩夹层。按照相关试验标准[9]规定,将取自该夹层的黏土岩芯通过钻取、断切、打磨流程,将岩芯加工成为直径50 mm、高100 mm的标准圆柱形试件。试验仪器采用MTS岩石力学试验系统,试验过程如下:
(1)用特制的高温膜将试件进行包裹并放置在试验机,依次安装渗透测试器、轴向应变计、环向应变计,并在三轴室注满油。
(2)以30 ℃/h的加温速率对三轴室内的油进行加温,待温度升至预定温度后,保持恒定温度30 min。
(3)对试件施加围压至5 MPa。
(4)施加荷载前对试样进行初始渗透率的测试,渗透压差均为1 MPa,之后施加轴向荷载,应力加载速率均为30 kN/min。
(5)应力增长过程中,每增加3 MPa左右时,就对试件进行1次渗透测试,然后在峰值处进行1次渗透测试,峰值以后视情况测试2~3次。
3 试验结果及分析
3.1 强度及变形分析
试验得到的三场耦合作用下黏土岩的应力-应变曲线见图1,其中σ1,σ3,ε1,ε3,εv分别表示试件的主应力、围压、轴向应变、环向应变、体积应变。应力-轴向应变曲线位于横坐标原点右侧,应力-环向应变曲线位于横坐标原点左侧,其余曲线表示应力-体积应变关系。
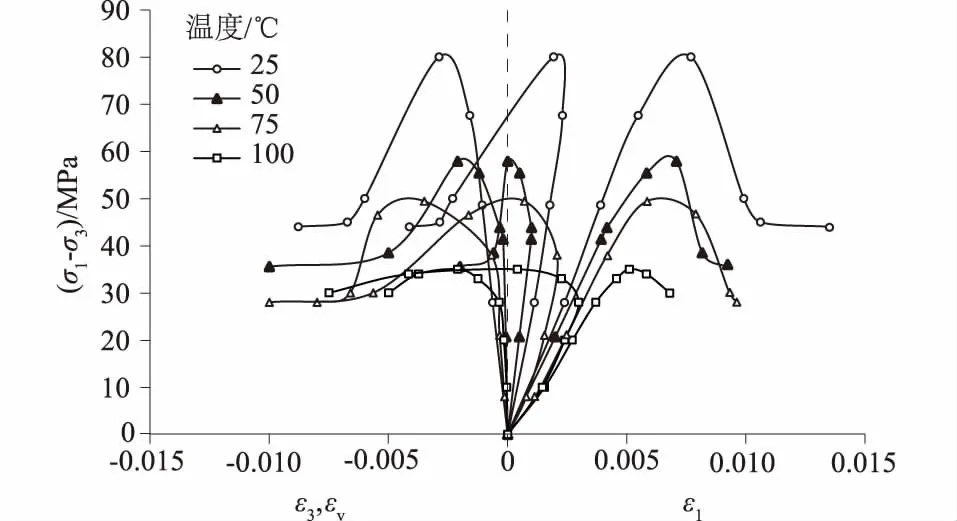
图1 黏土岩应力-应变曲线特征Fig.1 Characteristics of stress-strain curves of clay rock

图2 黏土岩强度特征Fig.2 Strength characteristics of clay rock
黏土岩温度-渗流-应力耦合情况下的变形过程包括压密、弹性、塑性、峰后残余变形4个过程。随着温度的升高,黏土岩的弹性模量越小,塑性变形越明显,但抵抗变形的能力越低,破坏形式逐渐由低温下的脆延性向高温时的弹塑性变化[10]。试样强度随着温度的升高呈线性减小(见图2),这是由于高温会使黏土岩内的矿物质成分发生部分分解变化,试件的内部结构逐渐由晶态向非晶态变化,颗粒与颗粒之间的胶结力也逐渐减小,而黏土岩也会呈现出热塑性和热软化反应,从而使试件的强度随之降低。
3.2 渗透特性分析
假设试件在渗流过程中保持温度不变,且为各向同性的均质材料,根据达西定律计算得到渗透率的计算式为
(1)
式中:k表示渗透率(μm2);p0表示渗透压差(MPa);Q表示渗流量(m3/s);μ为黏度系数(Pa·s),在25,50,75,100 ℃温度下μ分别取0.893 7,0.549 4,0.379 9,0.283 8 mPa·s;L表示黏土岩试件的长度(mm);A表示试件的横截面面积(mm2);p1,p2分别为试件上、下两端的压力值(MPa)。
将测试数据代入式(1)计算得到各温度、渗流、应力场下黏土岩的渗透率变化情况,见图3。

图3 应力及温度对黏土岩渗透率特征的影响Fig.3 Influences of stress and temperature on the permeability of clay rock
从图3可知,测试序号的渗透率呈阶段性的变化特征,大致呈先减后增的趋势,并在峰后阶段略有降低,即“降-升-回落”3个阶段特征。具体表现如下:
(1)压密变形阶段。由于原始微裂隙、微孔隙的挤压密实,渗透率会略有减小。
(2)弹性变形阶段。新生的微裂纹、微孔隙在应力作用下很快又被压实,试件内部处于损伤和硬化的平衡状态,因而渗透率也基本处于动态平衡阶段[11]。
(3)屈服变形阶段。损伤作用逐渐超过硬化作用并趋于主导地位,新生微裂纹、微裂隙开始发展并贯通,形成较大尺度的宏观裂纹与裂隙,使得渗透率逐渐加大,并在峰值应力前快速增加,在失稳破坏前夕达到最大值。
(4)残余变形过程中,试件内部再次发生应力的重分布,之前产生的部分裂纹和裂隙在应力作用下被重新压密闭合,试件破坏后产生的部分碎屑颗粒物会堵塞在渗流通道中,而峰后阶段采用应变控制使得轴向应力会出现松弛现象,裂纹扩展的速度因此而变缓,黏土岩的渗透率也就出现一定的回落现象。
从图3还可知,黏土岩的渗透率随温度的变化较为复杂,总体呈先减后增的趋势,即渗透率k100>k75>k25>k50。笔者总结前人研究成果和本次试验成果,认为存在如下原因:
(1)在一定温度内,由于温度升高,黏土岩试件内部产生膨胀,使得孔隙和裂隙变小,渗流通道减少,因而渗透率降低。当温度>50 ℃后,黏土岩内部的各种矿物成分开始发生物理化学作用,试件内部热损伤程度大于热膨胀效应,同时试件内部易挥发的物质成分随温度升高而流失,导致黏土岩的孔隙度增加,从而使得渗透率增大[12]。
(2)本文试验各试件虽然尽量保持取样深度、外观及试验条件等基本一致,但各试件之间仍存在一定的差异(即离散性),这也是造成上述情况的原因之一。
渗透率与变形之间的关系见图4。

图4 渗透率与变形之间的关系Fig.4 Relation between permeability and deformation
由图4可知,渗透率的变化与轴向应变呈良好的3阶段对应关系。
(1)压缩及弹性阶段。由于围压的侧向约束力,横向变形较轴向变形缓慢,此时黏土岩处于压缩硬化阶段,试件内部将调整至原位状态,原生裂纹和微孔隙在应力作用下会被迅速压密闭合[13],力学性能反而有所增强,因而渗透率也在降低一定值后保持基本恒定。
(2)当试件进入剪胀损伤阶段前后,新生裂隙逐渐发展贯通,横向应变开始加速增大,试件力学性质发生劣化,对应的渗透率也会加速增大,即表现为体应变的突变点是渗透率由平衡到快速增大的临界分界点。
(3)软化剪胀期间,体积应变快速增加,横向应变有所放缓,渗透率由于试件内部应力重分布和部分孔隙通道堵塞,因而略有降低。
3.3 损伤演化分析
损伤变量D反映了材料力学性质的破坏及劣化程度,假设Ad为黏土岩试件受损后的横截面积,Aw为黏土岩试件受损后横截面的孔隙面积,则有
D=Aw/Ad。
(1)
同时假设:黏土岩试件某半径为R的单元体在受损前后的体积分别为V,V′,密度分别为ρ,ρ′;r为黏土岩单元体出现的损伤球型空洞半径。根据物体的质量守恒定理,可得
(2)
体积应变εv的计算式为
(3)
式中:V0为黏土岩的初始体积;V1为三场耦合作用后的体积。同理,根据质量守恒定律,则有
(4)

图5 损伤变量与应变关系Fig.5 Relation between damage and strain
由试验得到的黏土岩试件的应力-应变曲线可知:低应力状态时,黏土岩处于压缩变形阶段,当加载应力值较大后,黏土岩试件发生剪胀损伤,试件处于膨胀状态,此时式(4)会出现无解情况。为此,定义和分析损伤变量D时,将体变压缩定为负值,并认为此时试件内部没有发生实质损伤(即虚拟损伤)[13],体变膨胀为正值,此时黏土岩试件发生剪胀实质性损伤,见图5。即有
(5)
根据上文分析,计算得到了各三场耦合作用下黏土岩的损伤演化曲线,见图6。从图6可以看到,在相同的应力、渗流场下,温度越高,黏土岩的实质损伤发展更快,但是各试件的虚拟损伤则呈现一定的无规律性,这主要与各试件的原生孔隙率、孔隙结构有关。

图6 不同温度下黏土岩损伤演化过程Fig.6 Damage evolution processes of clay rock at different temperatures
4 三场耦合损伤本构演化模型
假设黏土岩为横向和竖向的各向同性材料,得到了横观各向同性弹塑性损伤模型,损伤土体的损伤柔度矩阵[14-15]为
(6)
其中,

材料弹性损伤和塑性损伤演化规律分别为:
(8)
(9)

基于Mohr-Coulomb屈服函数,黏聚力损伤规律为
c=c0-c0-crDp。
(10)
式中:c为黏聚力;c0为初始黏聚力;cr为残余黏聚力。
基于上述分析,可通过MatLab自编程序反演计算得到各温度-渗流-应力环境下的黏土岩模型参数。以围压5 MPa,温度75 ℃为例,取Ev=600 MPa,Eh=1 350 MPa,Gvh=290 MPa,νhh=0.25,νvh=0.125,c0=25.3 kPa,其他参数均通过设定初始值后再以试验数据反演获得。模型计算采用有限元轴对称模型,直径和高度与试验试件一致,并同时约束水平自由度和径向自由度。采用数值计算可得到相应环境下的应力-应变曲线,见图7。

图7 模型反演分析结果与试验结果对比Fig.7 Comparison between model inversion analysis results and experimental results
由图7可以看到,反演计算得到的应力-应变曲线与试验曲线吻合良好,可见,本文所得的黏土岩三场耦合损伤本构模型能够较好地模拟各应力环境下的损伤演化过程,具有一定的合理性。
5 结 论
(1)温度对黏土岩具有明显的损伤劣化作用。随着温度的升高,强度、变形分别呈减小和增大趋势。
(2)渗透率随变形经历了“降-升-回落”3个阶段,与岩石变形损伤3阶段相对应,体变拐点为渗透率加速增大的临界分界点;温度越高,黏土岩的实质损伤发展越快。
(3)基于试验结果得到的黏土岩温度-渗流-应力三场耦合作用下的损伤本构模型能较好地模拟黏土岩的损伤变形特征。

