基于逆强化学习的空战态势评估函数优化方法*

李银通，韩 统，孙 楚，魏政磊

（1.空军工程大学航空工程学院，西安 710038；2.解放军94019 部队，新疆 和田 848099）

0 引言

空战态势评估指基于感知的环境信息，评估当前所处态势并预测态势发展［1］，是现代战斗机辅助决策系统的核心，也是UCAV 空战决策的重要组成部分［2］，对飞行器的作战使用及性能发挥有重要影响。

空战态势评估本质是建立从感知空战态势信息到态势值的复杂非线性映射关系。空战态势评估中，由UCAV 及所携带武器自身性能所决定的客观判断条件易于实现，如武器发射条件、飞行高度、飞行速度等是否满足；但高度、速度、角度、距离态势的权重分配，以及态势评估函数中参数的选取等非客观判断条件不易实现，一般做法是根据对实际空战情况的理解分析建立模型。目前，空战态势评估的常用方法主要有参量法与非参量法［1］。文献［3］提出基于动态威力场的空战态势评估方法，以战斗机的各项性能指标构建势场模型，解决了非参量法对动态环境处理能力不足的问题；文献［4］是典型的参量法，通过Bayes 方法分析目标特征的概率分布，以我机平均风险最小或完成任务概率最大为决策准则进行态势评估；文献［5］改进传统的评价指标，利用粗糙集理论建立了多指标综合评价模型。文献［3-5］均要求对实际空战过程有深入理解，并进行精确分析，例如贝叶斯方法中先验概率的选取、基于指标评估方法中的优势函数构造等。以上3 种方法过于依赖设计者个人对实际空战情况的片面理解，参数选取缺乏说服力，虽在特定的条件下能够取得较好的决策效果，却难以适应实际中复杂多变的空战态势。

本文提出的基于空战样本的态势评估较好地解决了上述问题：逆强化学习可以实现对大量空战样本数据的知识提取，从而逼近从参数信息到态势值的复杂映射关系，回避了态势评估函数中非客观判断条件的复杂设计，解决了传统态势评估函数设计中受人为因素影响过大的弊端。

本例以逆强化学习（Inverse Reinforcement Learning）为基础分析空战样本数据，进而得到态势评估函数，再通过强化学习（Reinforcement Learning）以改进策略，将其应用于UCAV 空战态势评估中，可充分发掘空战数据中的态势信息，再通过粒子群算法以及Sigmoid 函数处理态势信息，以实现对态势评估函数参数的优化。整体结构如图1 所示。

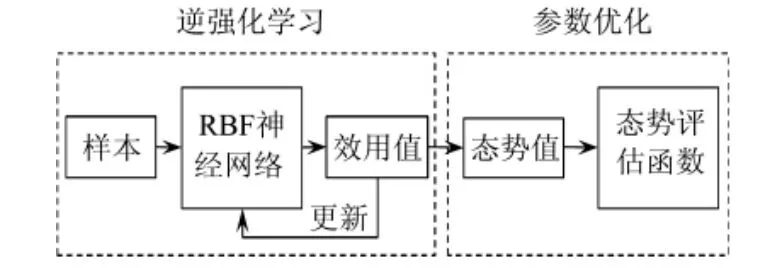
图1 态势评估函数设计结构

1 基本模型

1.1 基本态势评估函数

采用逆强化学习方法提取态势评估函数时，若将态势参数信息到态势值的映射关系作为黑箱系统考虑，计算复杂，无法充分利用已有的先验知识，同时结果的可解释性较差。但是，若将已知的信息进行公式化表示，公式化表示过程中只保留难以确定的参数作为未知量，便将对整体态势函数的优化问题简化为对部分参数的优化问题，简化了计算过程。

依据文献［6-10］中对空战态势评估的研究成果，将态势评估函数分为角度优势函数、速度优势函数、高度优势函数、距离优势函数以及效能优势函数。对由飞机系统性能确定的固有判断条件，直接给出确定结果。

1.1.1 角度优势函数

设雷达最大搜索方位角为φR，导弹最大离轴发射角为φM，不可逃逸区圆锥角为φK。设计角度优势函数为：

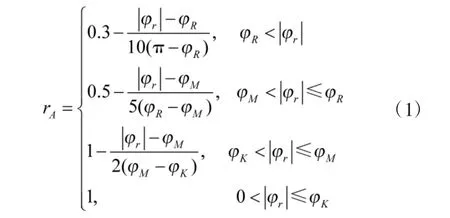
1.1.2 速度优势函数

设vrm为本机最佳空战速度，vr，vb分别为本机、敌机的速度，设计速度优势函数为：

当vrm＞1.5vb时

当vrm≤1.5vb时

1.1.3 高度优势函数

设hrm为本机最佳空战高度，hr，hb分别为本机、敌机飞行高度，设计高度优势函数为：

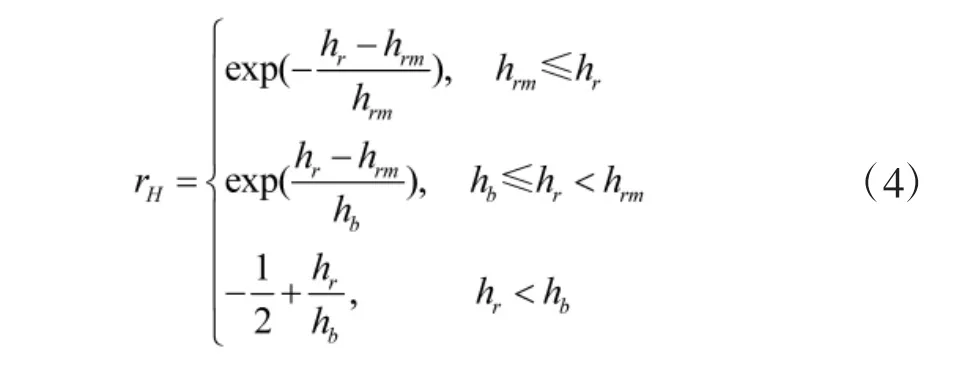
1.1.4 距离优势函数

设雷达最大搜索距离为dR，导弹最大攻击距离为dM，导弹最大不可逃逸距离为dKmax，导弹最小不可逃逸距离为dKmin。设计距离优势函数为：

1.1.5 效能优势函数

空战效能由飞行器及携带武器的性能决定，不需进行估计与优化，令TE表示空战效能优势。

当我机导弹满足发射条件时rc=10，当敌机满足导弹发射条件时rc=-10，否则rc=0；当满足条件：h＞20 000 m 或h＜200 m 或v＞300 m/s 或v＜50 m/s时，re=-10；其余条件下re=0。

1.2 利用Sigmoid 函数优化态势评估函数

为提升态势评估函数对复杂空战环境的适应能力，本例并非直接将各个态势值的和作为总体态势评估函数，而是利用带权重ωr，βr的Sigmoid 函数对态势评估函数进行优化，均衡了rA，rV，rH，rD之间的差异，使各个态势值保持在一定的范围，避免因单个态势值差异过大而影响整体评估效果。带权重ωr，βr的Sigmoid 函数为：

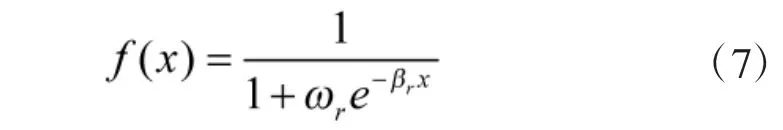
将rA，rV，rH，rD作为Sigmoid 函数的自变量输入，可得到参数可调的态势评估函数分别为：

其中，ωri，βri，i=1，2，3，4 为待优化参数。式（8）～式（11）中分子为原态势值，其限制了Sigmoid 函数对整体态势值的压缩作用，避免了态势值在接近0 时导致态势的累加效应不明显，降低了其对不同态势的区分度。综上，整体态势评估函数可表示为：

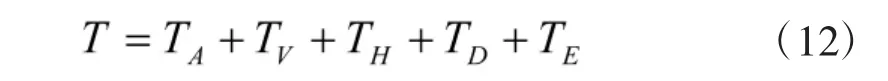
解出最优ωri，βri，即实现对态势评估函数优化。

2 空战态势评估函数提取与优化

逆强化学习以输出的效用值V（xt）作为输入状态xt的评价指标，所以必须提取从xt到V（xt）的映射关系。本文应用的重点在于计算效用值V（xt），考虑到RBF 神经网络非线性逼近能力强，结构简单的特点，故选用它来进行效用值函数的逼近。

逆强化学习所用样本为空战中状态序列，输入RBF 神经网络后输出估计效用值，并依据误差不断修正网络参数，直到满足条件。采用训练完成的网络计算所有样本的效用值序列，依据时序差分学习的值函数更新规则

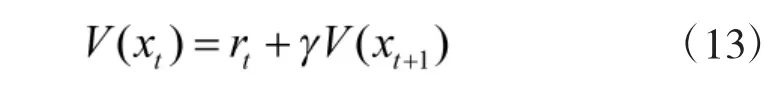
式中，γ 为折扣率，设定为γ=0.9，在各个状态的效用值序列已知时，即可求出所有状态对应的态势值rt。最后计算态势评估函数中的未知参数，使其对状态的评估值与态势值r 的误差在允许范围内，即完成了对态势评估函数的优化。

对式（13），在逆强化学习中rt未知，导致无法更新效用值序列，因此，无法在单一样本下训练该RBF 神经网络。本文设置两类样本：正例样本集与反例样本集。训练完成的RBF 网络可以实现：对正例样本集的估计效用值大于对反例样本集的估计效用值。

2.1 训练样本与评价指标

空战样本数据为特定的决策与机动动作序列，若空战中决策进行n 步，则样本轨迹S 可表示为：

其中，xi表示状态，ai表示在状态xi下采取的机动决策动作。

正例样本集：击落敌机的决策轨迹，记为S1；反例样本集：被敌机击落的决策轨迹，记为S0。

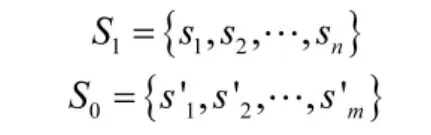
其中，si与si'分别表示一次空战的决策轨迹。由于逆强化学习输入仅为状态序列x，所以忽略样本集中决策轨迹动作，仅记录状态：

对于决策轨迹状态集S1与S0，记RBF 神经网络对其效用值的估计为：

2.2 RBF 神经网络的值函数逼近

本文逆强化学习方法基于多输入单输出RBF网络，主要完成由状态x 到效用值V（x）的映射关系，基本结构如图2 所示。

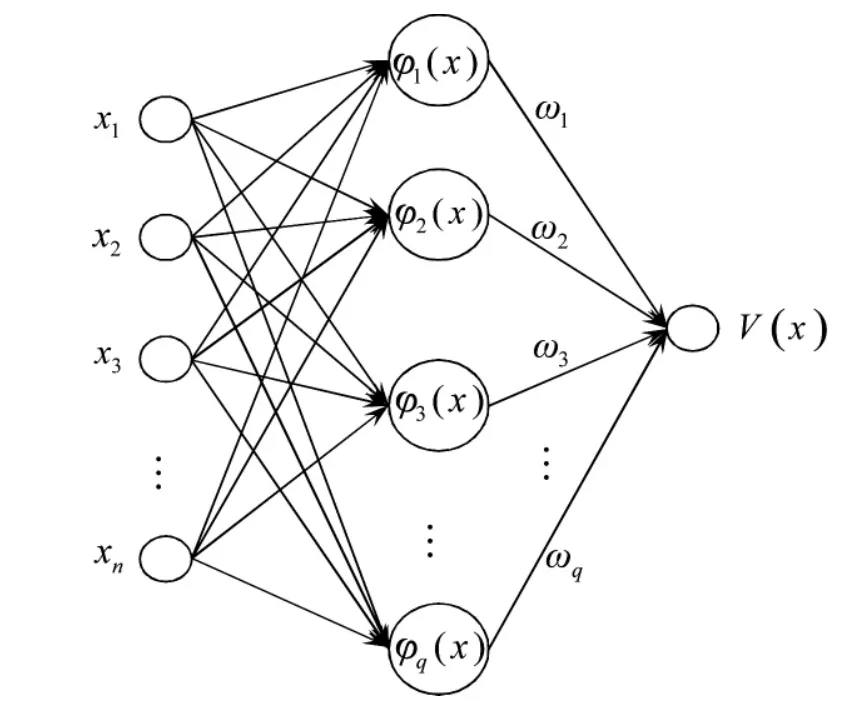
图2 多输入单输出RBF 网络结构

输入层到隐层的非线性映射采用高斯函数为基函数，含有q 个隐层节点的RBF 网络可表示为：

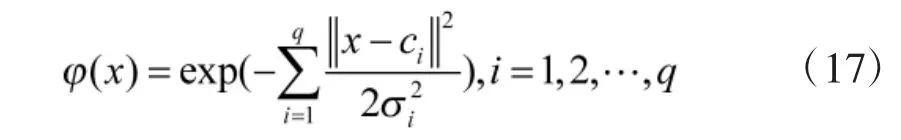
其中，x 为输入状态变量，ci为第i 个基函数的中心，σi为基函数中心的宽度。

设RBF 神经网络输出值为y，输出层的线性映射表示为：

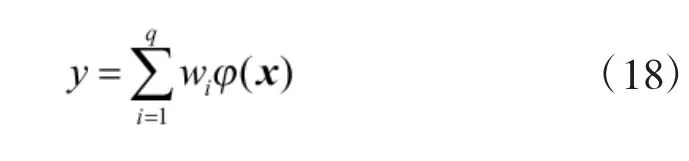
其中，wi表示各个隐层连接节点的权重。

本文仅以输出层的各个连接节点的权重wi为例，推导满足式（16）的RBF 神经网络参数更新公式。设RBF 神经网络输出估计效用值V（xt），由式（17）、式（18），样本集S1与S0的平均效用值可表示为：

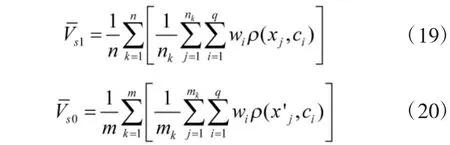
设学习率为ηw，对E 求关于wi的负导数，wi的更新公式可表示为：

其中，

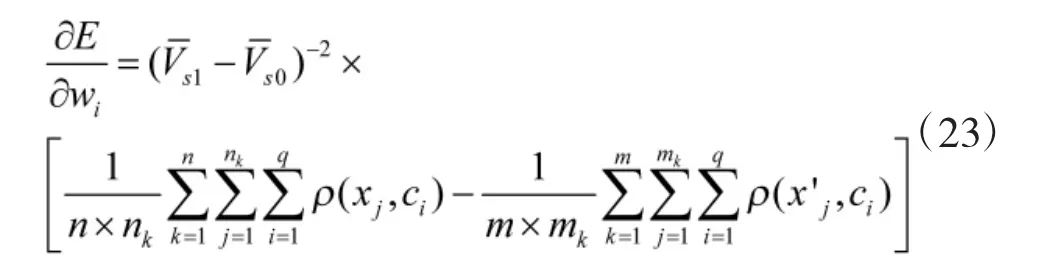
同理可以得到参数βi与向量ci的更新公式为：

其中，ηβ与ηc为对应参数的学习率。

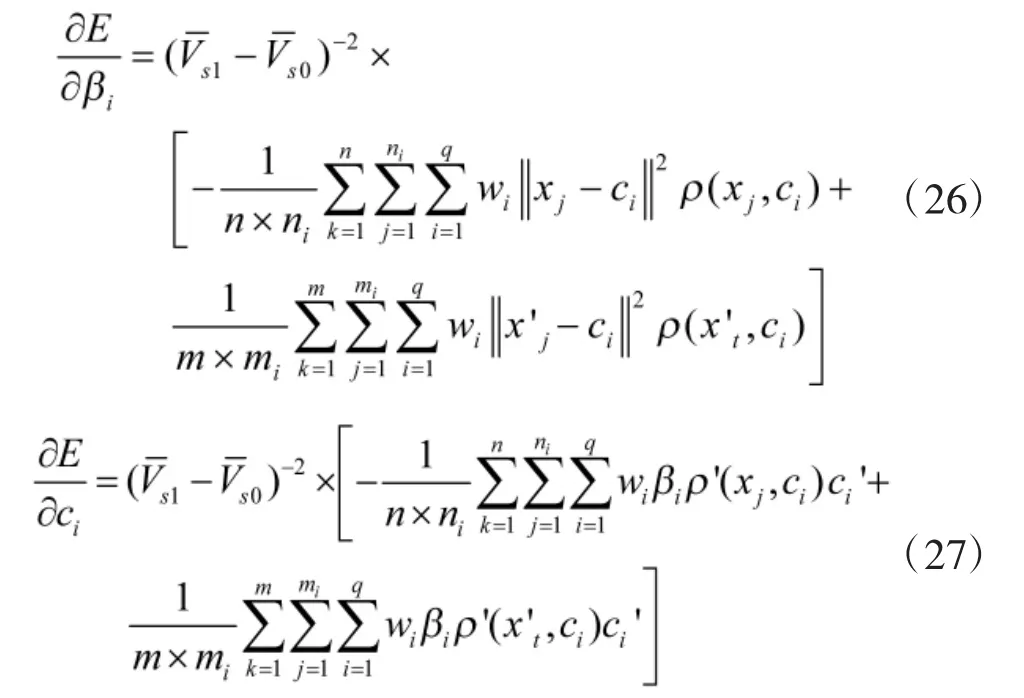
当评价指标E 满足式（16）时，RBF 神经网络训练完成。

2.3 态势评估函数的优化与参数求解

依据式（17）～式（27），可对RBF 神经网络进行训练，得到样本的效用值序列，由式（13），可计算每个状态瞬时态势值rt，表示为：

设样本瞬时态势值序列的集合为：

其中，

将样本中的状态序列输出作为态势评估函数，同样可以得到每个样本的态势评估值。当由态势评估函数得到的态势评估值与通过逆强化学习方法提取的态势值相差较小时，表明态势评估函数的性能较好；反之，如果两者差异过大，则说明态势评估函数误差过大，需要进行参数更新。

综上，态势评估函数的优化问题可表述为：对函数T，修正其中的ωri，βri，使其对S1与S0的输出值满足

对于式T=TA+TV+TH+TD+TE的参数优化问题，由于缺乏ωri，βri的先验知识，所以初值设定比较困难。但考虑到该问题维度不高，且目标函数比较简单，故本文采用自适应粒子群算法进行态势评估函数优化问题中的最优参数求解。由于篇幅限制，不再赘述该算法相关原理。

3 仿真实验

3.1 态势评估函数的提取仿真

本文选择了两组典型的空战机动动作：后置跟踪滚转机动与高速Yo-Yo 机动作为样本提取态势评估函数。正例样本为后置滚转机动，反例样本为高速Yo-Yo 机动。图3 与图4 为两组机动中双方的飞行轨迹，红色为我机轨迹，蓝色为敌机轨迹。通过Simulink 仿真实现机动动作，仿真运行40 s，并以0.036 s 为时间间隔记录空战时间内对抗双方的状态变量，作为RBF 神经网络的输入。

图3 后置跟踪滚转机动轨迹

图4 高速Yo-Yo 机动轨迹

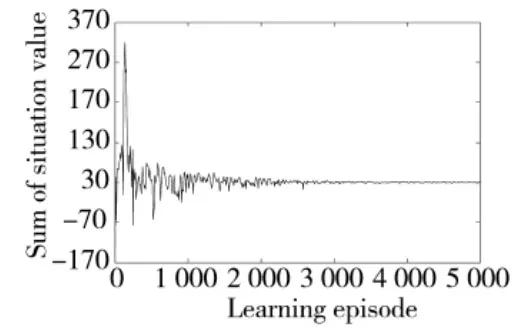
图5 正例样本总态势值

图6 反例样本总态势值

图7 训练后期两类样本差值

训练初期，由于网络参数的随机性，其对正例反例样本的态势值的估计波动较大；训练后期，两类样本估计态势值之差逐渐稳定，此时RBF 神经网络对正例样本的态势估计值大于反例样本；最终指标在误差范围内，对两类样本的估计态势值差值稳定在4.035 附近，大于（Emax）-1=2，RBF 神经网络的训练完成。

3.2 态势评估函数性能分析

由上节中得到的态势值序列，采用自适应粒子群算法求解态势评估函数中的最优参数。态势评估函数中的参数设置为：φR=65°，φM=35°，φK=20°，vrm=200 m/s；hrm=2 000 m；dR=60 km；dM=10 km，dKmax=5 km，dKmin=1 km。自适应粒子群算法参数设置为：minΔr=0.1，c1=c2=2，ωmax=0.9，ωmin=0.6，粒子数取100，迭代步数取150。得到适应度变化曲线如图8 所示。

图8 粒子适应度曲线

各个变量对应最优权重为：ωr1=0.870 4、ωr2=0.516 2、ωr3=0.646 9、ωr4=0.302 0、βr1=0.291 7、βr2=0.120 7、βr3=0.049 1、βr4=0.355 7。

结果表明，近距空战最重要的影响因素为角度优势，所占权重最大，其次是速度优势与高度优势，而距离优势的所占权重最小，与近距空战实际相符。

将改进后的态势评估函数用于UCAV 机动决策与改进前进行对比。这里给出不同仿真条件下态势值随训练次数的变化，以观察态势评估函数对策略收敛速度的影响，结果如图9，图10 所示。

图9 态势评估函数随训练次数变化曲线1

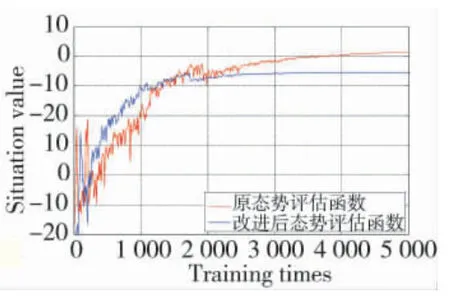
图10 态势评估函数随训练次数变化曲线2

从图9，图10 中可以看出：改进后的态势评估函数提升了态势值的收敛速度，两种仿真条件下，改进后态势评估函数均比未改进的提前收敛到最优策略。

对态势评估函数的优化过程中使用Sigmoid 函数的压缩作用，导致整体态势值的降低，对比双方态势值的差异，如图11 所示。

图11 10 次训练中的态势值

改进后的态势评估函数，决策系统在10 次训练中的态势均值为9.889 0，方差为0.174 2；而未改进态势评估函数决策系统的态势均值为13.179 6，方差为0.394 1，方差的降低说明改进后的态势评估函数增强了决策系统的稳定性；总态势值的降低，保证了较好的区分度，并加快了UCAV 学习的收敛速度。

4 结论

本文提出的以RBF 神经网络为基础的逆强化学习方法，解决了强化学习在UCAV 自主决策中的态势评估函数非客观判断条件设计困难的问题；创新性设计了基于Sigmoid 函数参数可调的空战态势评估函数；采用自适应粒子群算法，依据逆强化学习的输出结果对原态势函数中的参数进行优化。通过对比，证明该方法能够提升无人机自主决策系统的策略收敛速度与稳定性，克服了传统奖赏函数设计中主观性过强的缺点，较好地提升了其对不同空战态势的适应能力。