一种特殊结构双基地雷达的空射诱饵信号特征*
杨立明,韦 高,尉建利
(1.西北工业大学电子信息学院,西安 710072;2.西北工业大学航空航天学院,西安 710072)
0 引言
空射诱饵是一种廉价的自主飞行器,能够高度逼真地模拟真实飞机的速度和雷达反射截面积。空射诱饵能够造成预警探测体系的虚警率提高,并且可以诱骗防空导弹攻击,大量耗费敌防空导弹。通过使用空射诱饵,可以大大提高作战飞机的突防成功率,是一种十分有效的突防突击手段。空射诱饵通常使用信号增强设备来达到与作战飞机相当的信号强度,并且其速度与作战飞机相当,使得雷达很难识别诱饵。
近年来,美军研发和列装了一系列空射诱饵。美军的空射诱饵通过复制美及盟国作战飞机的飞行剖面和信号特征,达到欺骗、干扰对方雷达的目的。国内对于空射诱饵的研究主要集中在空射诱饵的发展情况和特点上[1-10],鉴于空射诱饵的巨大威胁,如何识别空射诱饵成为一个重要的课题。但是,对于空射诱饵的信号特点以及如何识别空射诱饵的研究未见报道。
本文分析了空射诱饵在单发双收双基地雷达中的信号特点。首先建立了发射信号模型,然后分别分析了两个接收站的回波信号的时延和多普勒特征,建立了信号模型。并在频域和分数阶傅里叶变换域对两个接收站的信号特点作了深入分析,分析结果对于利用这种特殊结构的双基地雷达来识别诱饵具有一定的参考价值。
1 空射诱饵作用机理
空射诱饵是一种空射型战术诱饵,通过模拟载机运动和雷达散射特征,达到诱骗敌雷达产生虚警,扰乱敌防空体系,提高载机生存能力的目的。空射诱饵还可以作为侦察和干扰平台,对敌实施纵深侦察和抵近干扰。国外许多国家都十分重视空射诱饵的研制,包括美国、俄罗斯都在开发自己的空射诱饵,并显示了很好的作战效果。
为了更好地欺骗敌方雷达,空射诱饵使用了信号增强设备来增大转发的信号强度,增大被敌方雷达识别的几率。空射诱饵的飞行速度和高度均与作战飞机基本相当,仅通过单个雷达很难识别出诱饵。空射诱饵的信号增强设备作用范围主要限于前向,对后向通常不专门增强信号。这主要是因为空射诱饵模拟的是突防突击飞机,敌方雷达对其探测的方向也来自于前向。
2 空射诱饵在单发双收双基地雷达的信号模型
2.1 单发双收双基地雷达结构

图1 单发双收双基地雷达结构

2.2 发射信号模型
采用脉冲压缩技术的雷达发射信号可以写为[11]:

2.3 接收站信号模型
接收站1 的接收信号为信号增强设备信号与回波信号的叠加。信号增强设备的信号是转发发射信号形成的,信号形式与发射信号一致,区别在于相对发射信号时间基准的延迟和叠加的频移。则该信号可以表示为

接收站1 接收的诱饵本体反射的回波信号可以表示为
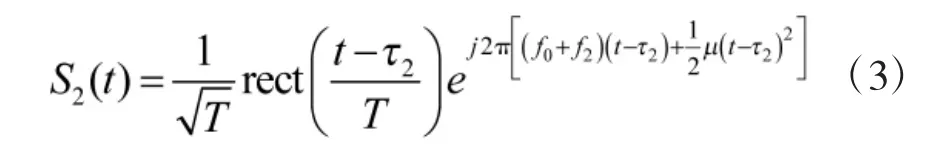
接收站1 的接收信号即可表示为
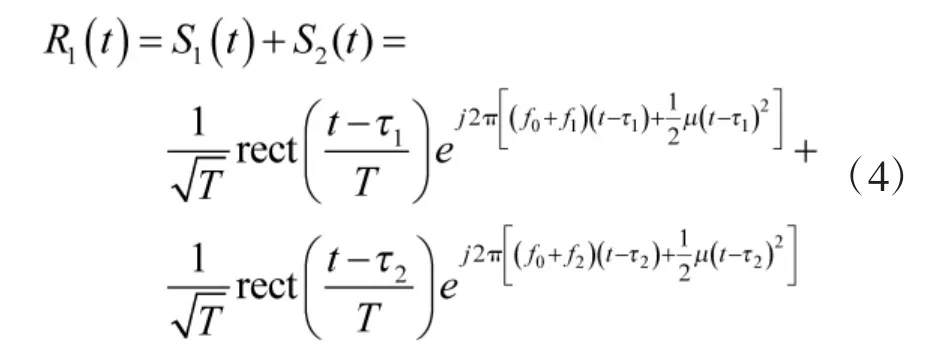
接收站2 处于诱饵的后方,接收的信号不包含信号增强设备的转发信号,仅有诱饵本体的后向回波信号,该信号可以表示为

相对于信号增强设备的转发信号,诱饵本体在接收站1 和接收站2 的回波信号在时延和频移上具有与双基地雷达结构相关的特性,该特性与诱饵相对于两个接收站的位置和飞行速度密切相关。
3 接收站信号的时域和频域特性
接收站1 和接收站2 的接收信号均是以发射信号为基础产生的,二者接收的信号是由相同调频率的线性调频信号叠加而成,区别在于时延和多普勒频率。因此,在时域很难区分两个接收站的信号。设发射信号载频为10 GHz,带宽为30 MHz,脉宽为10 μs,脉冲重复周期为500 μs,S1(t)、S2(t)和S3(t)的时延和多普勒频率分别为300 μs、13.1 kHz,350 μs、13.5 kHz,450 μs、14 kHz,则两个接收站信号的时域、频域波形如图2、图3 所示,可以看出,两个接收站的信号波形混叠后难以区分。
假设两个接收站采用与发射信号匹配的滤波器分别处理接收的信号,线性调频信号的匹配滤波器频率特性可以写为[11]:

则两个接收站接收信号经该匹配滤波器处理后输出的频谱分别为

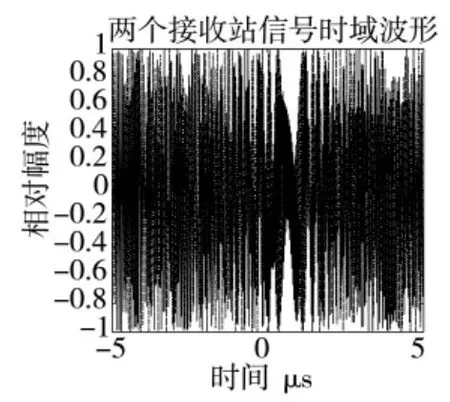
图2 两个接收站信号时域波形
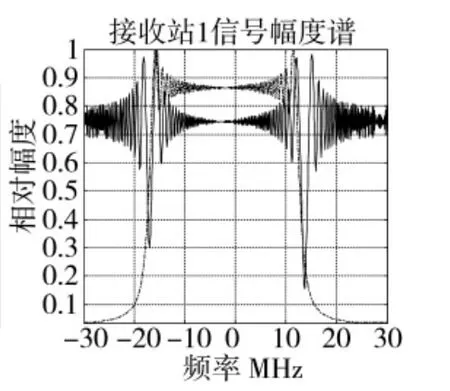
图3 两个接收站信号频谱图
经过对式(7)、式(8)作傅里叶逆变换,可以得到两个接收站信号经过匹配滤波处理后的输出信号分别为

仍旧采用仿真两个接收站时、频域信号波形参数计算经匹配滤波输出的信号,如图4、图5 所示。

图4 接收站1 的匹配滤波输出

图5 接收站2 的匹配滤波输出
可以看出,信号增强转发的信号经过匹配滤波处理的输出与诱饵本体反射的信号匹配滤波器输出都获得了处理增益。接收站1 的诱饵本体信号相对于转发信号强度要弱30 dB,因此,信号增强设备的信号能够完全遮盖住诱饵本体回波,接收站1 本身无法分辨出诱饵本体和转发信号。即仅靠单站雷达接收机的匹配滤波难以分辨诱饵本体信号。在接收站2 的诱饵本体信号也获得了处理增益,能够输出一定强度的信号。但是,这里的仿真仅仅是根据诱饵产生的信号在两个接收站经匹配滤波处理后的处理结果,尚未建立起与双基地雷达结构相关的特性。下面具体分析双地雷达结构确定后,诱饵信号在两个接收站的输出信号的特点,并通过关联两个接收站的匹配滤波输出,获得识别诱饵的信号特征。
4 诱饵本体信号时延和多普勒频移特点
根据图1 所示的双基地雷达结构,在t 时刻目标到发射站的距离可以通过余弦定理计算
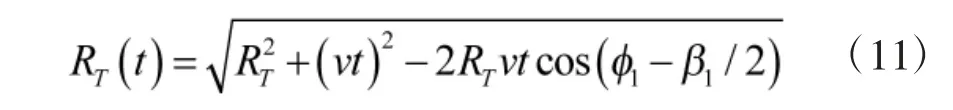
式(11)中,RT为初始时刻目标与发射站的距离。
同理可以计算得到目标到两个接收站的距离分别为

式中,RR1、RR2分别为初始时刻目标与两个接收站的距离。
为分析方便,把式(11)~式(13)分别在初始时刻展开成泰勒级数并忽略高次项,则式(11)~式(13)分别表示为
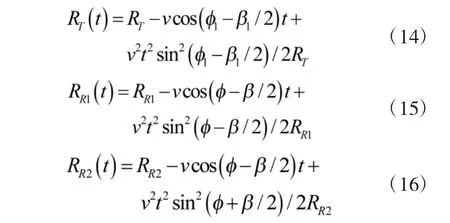
则t 时刻接收站1 和接收站2 的双基地距离和分别为

进一步可以计算得到目标在两个接收站的时延分别为
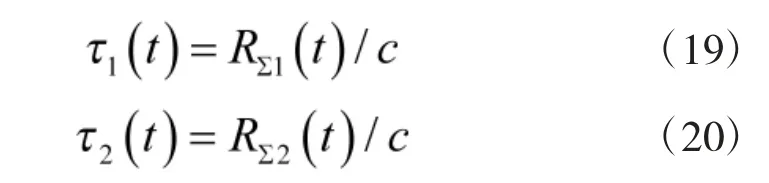
式(19)和式(20)中,c 表示光速。
为了比较目标在两个接收站的时延,可以计算两个接收站时延差

考虑到在目标运动的时间内,目标运动距离比目标与发射站和接收站的距离小得多,因此,可以忽略泰勒级数展开式中的二次以上导数项。式(21)则可以简化为

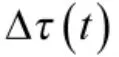

式(23)中,θR2为接收站2 相对目标的视角。推导过程中,利用余弦定理确定了关系式[13]

将式(23)、式(24)代入式(22)可得

式(25)即为两个接收站目标回波信号时延差在t 时刻与双基地结构参数的关系式。
设目标速度为200 m/s,运动速度方向角100°,两个接收站间距离为150 km,接收站2 距离目标100 km,与目标视角为120°。则两个接收站时延差随目标运动时间的关系见图6。
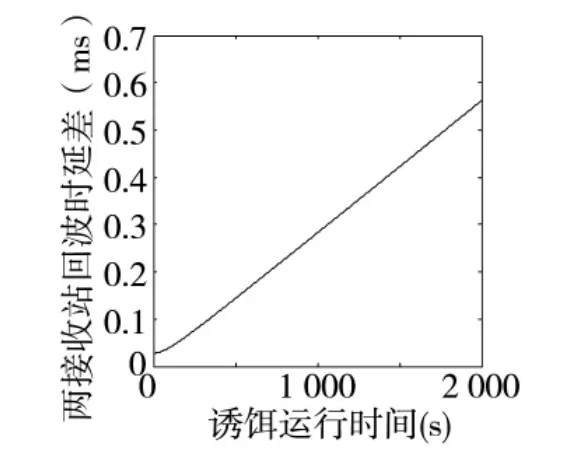
图6 两接收站回波时延变化图
由图6 可以看出,两接收站的回波时延随着诱饵运行时间的增长而不断增加,并且呈线性关系。因此,在双基地雷达的两个接收站探测到诱饵后,诱饵本体的回波信号的时延会存在稳定的线性关系,相对而言,针对运行方向辐射信号的信号增强设备发射的信号只会被接收站1 接收,其时延与接收站2 的回波延迟则不存在稳定的线性关系。
双基地雷达中的多普勒频移为[13]
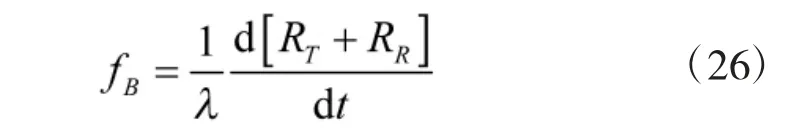
将式(17)、式(18)代入式(26)可得接收站1 和接收站2 目标回波信号的多普勒频移分别为


在图1 中,t 时刻接收站1 和接收站2 的双基地距离和均包含了发射站到目标的距离RT(t),而两个接收站的多普勒频移的计算均需要计算距离和对时间的微分,由于微分计算是线性的,在计算二者的多普勒频移差时,首先计算二者的距离和之差再对时间微分,即可抵消发射站到目标的距离,只需要计算目标到两个接收站的距离对时间的微分。
利用图1 中的位置关系,可以直接计算两个接收站接收的目标回波信号的多普勒频移,多普勒频移的定义为[14-15]

其中,vr为目标速度矢量在雷达方向的分量。接收站1 和接收站2 的多普勒频移分别为

两个接收站的多普勒频移差为

可以看出,式(33)与式(29)完全一致,证明前面分析过程的正确性。式(33)没有时间分量,说明两个接收站的多普勒频移差与时间没有关系,仅与双基地雷达结构参量有关。把式(23)代入式(33)可得
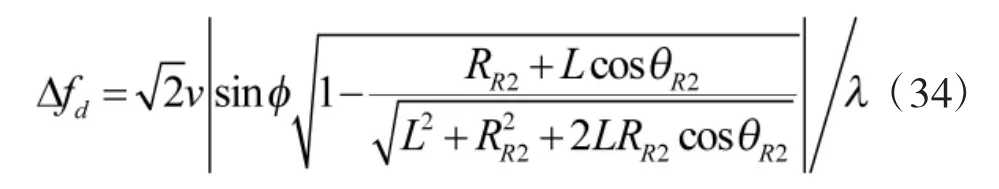
由式(34)可以确定多普勒频移与双基地雷达结构参量的具体关系。在目标速度和飞行方向确定后,通过双基地雷达的两个接收站的距离、一个接收站与目标的距离和对应的视角,即可确定两个接收站目标回波信号的多普勒频移差。设定不同的双基地角,计算目标速度矢量方向角与多普勒频移差的变化关系如图7 所示。

图7 多普勒频移差与诱饵速度方向角关系图
由式(34)可知,两个接收站的频移差与诱饵运行时间无关。仅与初始双基地角和诱饵飞行方向有关。在双基地结构和工作频率确定后,频移差则仅与诱饵的飞行方向有关。
由图7 可以看出,两个接收站的归一化多普勒频移差最大值不超过1,这说明诱饵本体在两个接收站的多普勒频移受限于双基地雷达的结构,二者的多普勒频移差有相对稳定的限值。通过式(33)和图7 可知,在目标飞行方向与双基地角平分线垂直时,两个接收站的多普勒频移差值最大,其余方向的多普勒频移差均小于该方向差值,这也是两个接收站多普勒频移的最大限值。另外,在诱饵速度方向相反的角度上,两个接收站的多普勒频移具有相同的差值。
诱饵的信号增强设备通常设置一定的多普勒频移,该多普勒频移的辐射信号通常被某一个接收站接收,而另一个接收站则无法接收,相当于两个接收站分别接收了信号增强设备的多普勒频移和诱饵本体的多普勒频移,这两个多普勒频移之差无法保持式(34)的关系,没有稳定的频移差。
5 结论
为了进一步分析两个接收站的信号特征关系,本文建立了雷达发射信号经诱饵本体反射后在两个接收站的时延差和多普勒频移差的模型,分析得出了信号时延差和多普勒频移差与诱饵运行时间和双基地雷达结构参量的关系,证明两个接收站的时延差和多普勒频移差具有稳定的关系(在特定方向使用信号增强设备辐射的信号,被双基地雷达特定接收站接收的诱饵信号,增强设备辐射信号与另一个接收站接收的诱饵本体辐射信号的时延差和多普勒频移差,则不具备本文分析的稳定关系)。分析结果对于利用该类特殊结构的双基地雷达探测识别诱饵具有一定的参考价值。

