一类整数阶分数阶幸福模型的滑模同步

王东晓，王战伟

(郑州航空工业管理学院 数学学院,河南 郑州 450046)

科研工作者抽象出很多动力学模型，并从系统的各个方面加以研究，得到很多结果[1-8].文献[1]研究了爱情的分数阶动力模型;文献[2]对一个对称分数阶经济模型的混沌特征加以研究和分析;文献[3-4]研究了分数阶混沌系统和一类分数阶非线性混沌系统的同步问题;文献[5-7]研究了爱情的幸福模型，其中文献[5]基于特征值方法研究了幸福的动力学模型，文献[8]研究了受驱动非线性幸福模型的动力学解析问题.

20世纪50年代,前苏联学者提出变结构控制.变结构控制起源于继电器控制和 Bang-Bang 控制，它与常规控制的区别在于控制的不连续性.滑模控制(sliding mode control, 简称SMC)也叫变结构控制，本质上是一类特殊的非线性控制，且非线性表现为控制的不连续性.滑模变结构控制的原理:根据系统所期望的动态特性来设计系统的切换超平面，通过滑动模态控制器使系统状态从超平面之外向切换超平面收束;系统一旦到达切换超平面，控制作用将保证系统沿切换超平面到达系统原点，这一沿切换超平面向原点滑动的过程称为滑模控制.文献[9]对分数阶磁悬浮球系统进行了滑膜控制;文献[10]基于滑膜控制对挠性航天器姿态跟踪及主动振动抑制加以研究;文献[11-12]分别研究了神经网络和一个新的分数阶混沌系统的滑模同步问题.另一方面，当遭遇一个外来事件的激励后，情绪会有多种响应表现，表现为忘乎所以歇斯底里(超混沌)，或者原来不安的情绪突然安静下来.论文运用李雅普诺夫稳定性理论及分数阶微积分，采用滑模控制，分别研究了一类整数阶、分数阶的2，3维幸福模型的同步问题.

引理1Caputo型分数阶微分算子的Laplace变换为

其中：n-1≤p≤n，且当0≤p<1时，有

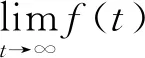
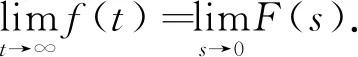
1 主要结果

Sprott等[5]研究罗密欧与朱丽叶彼此相爱的时间振荡关系，构造爱情R的动力学模型为

其中：β为阻尼衰减率，ω为自然谐振频率.

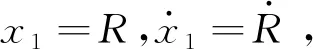
(1)

以系统(1)为驱动系统，考虑如下响应系统

(2)

其中：U(t)为控制器.定义误差为e1=y1-x1,e2=y2-x2.

(2)式减去(1)式得到误差系统为

(3)

定理1设计滑模函数s(t)=εe1+e2,ε>0，控制器U=(β-ε)e2+ω2e1-ηsign(s(t))，η>0，则系统(1)，(2)滑模混沌同步.

证明设计滑模面s(t)=εe1+e2，当系统发生滑模运动时，需满足条件

(4)

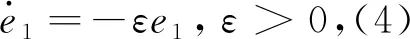
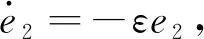
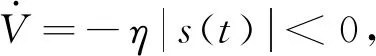
其次,考虑2维分数阶幸福模型,有

(5)

响应系统为

(6)

定义误差为e1=y1-x1,e2=y2-x2,则误差系统为

(7)

(8)

取1-α分数阶导数

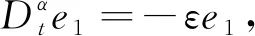
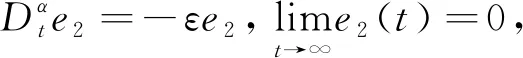
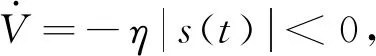
(9)

响应系统为

(10)

取误差变量为e1=y1-x1,e2=y2-x2,e3=y3-x3，得误差系统为

定理3设计滑模函数s(t)=εe1+e2+e3，ε>0.25，选取控制器

则系统(9)，(10)是滑模同步的.

证明设计滑模函数s(t)=εe1+e2+e3，当系统发生滑膜运动时，需满足条件

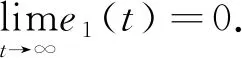
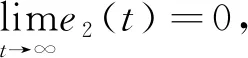
代入

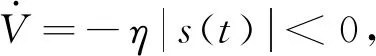
以下考虑分数阶3维幸福模型.驱动系统为

(11)

响应系统为

(12)

系统(12)减去(11),得到误差系统为

(13)

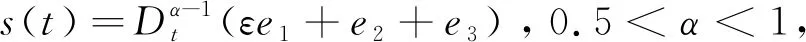
则系统(11)，(12)是滑模同步的.

证明滑模函数

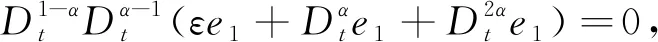
应用引理2，有

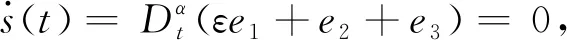
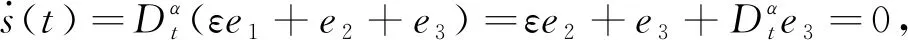
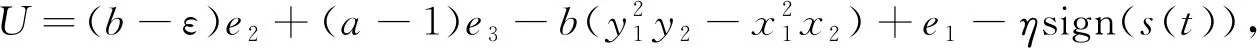
幸福模型对人们的心理治疗和处世方式可以起到积极作用.利用数学方法，构建幸福的动力学模型和分析，实现幸福模型的同步，可以提高整个社会的幸福指数.

2 数值仿真及结语

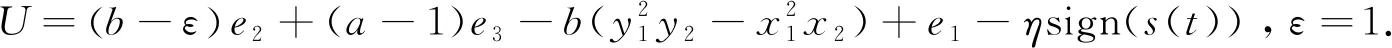
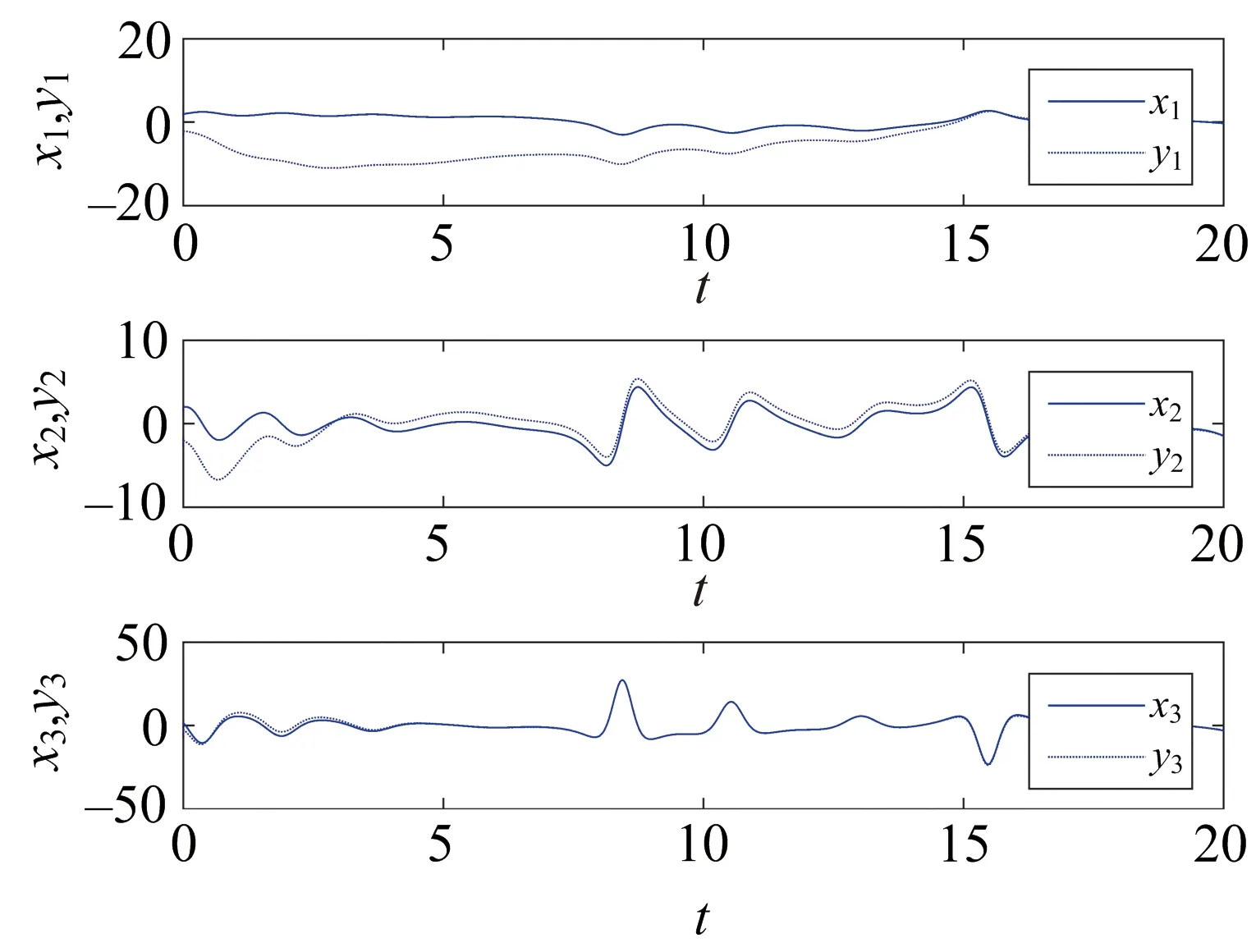
图1 系统(9),(10)的同步曲线

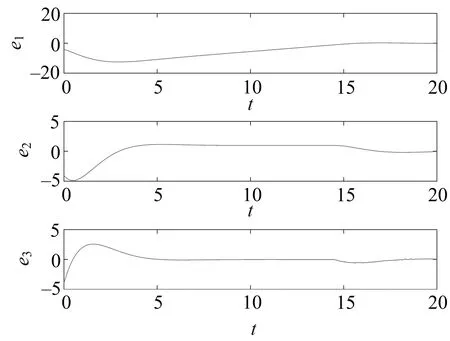
图2 系统(9)，(10)的误差曲线

论文用滑模控制实现了一类幸福模型的控制,由于得到的是充分条件而非必要条件，故在数值仿真过程中,即使是更为简单的控制器同样可以实现系统的同步,所以,有更多的问题需要后续去研究.