激光辐照下圆锥体空间碎片的激光烧蚀力与力矩分析方法

吴波，金星

(航天工程大学激光推进及其应用国家重点实验室，北京 101416)

1 引言

人类航天发射活动的日益频繁，导致空间碎片的数目已经增长到严重威胁人类航天活动的程度，因此清除空间碎片已经成为航天国家的共识[1-3]。其中尺寸为1～10cm的厘米级碎片由于数目较多难以机动规避、尺寸较大难以结构性防护，成为了清除研究的主要对象[4]。而在诸多清除方式中，天基激光清除空间碎片方法由于其高效及时等特性，得到了广泛关注和研究[5-8]。

激光清除空间碎片的原理是脉冲激光烧蚀碎片表面，由冲量耦合效应产生反喷冲量使碎片减速降轨，直至坠入大气层中烧毁[5]，因此精准地计算碎片变轨参数、掌握碎片坠落轨迹是非常重要的一环。而由于碎片几何形状的差异，不同角度的激光烧蚀会产生不同的烧蚀力与烧蚀力矩。因此，本文选择圆锥体碎片为研究对象，计算不同角度激光烧蚀产生的不同效果，对激光清除空间碎片具有重要意义。

2 圆锥体碎片的激光辐照区域与投影区域分析

圆锥体 (底面半径为R＞0，高为H＞0，满足高径比H/R=tanε)为轴对称，以底面圆确定Oxy平面，底面圆心为坐标原点O，对称轴为z轴，激光入射方向所在平面确定Oyz平面，建立如图1所示坐标系Oxyz。将激光入射方向与y轴正向夹角记为θ(即激光仰角为θ)，满足-π/2≤θ≤π/2，则激光方向单位矢量m=(mx，my，mz)=(0，cosθ，sinθ)，圆锥体质心位置为 (xc，yc，zc)=(0，0，H/4)。

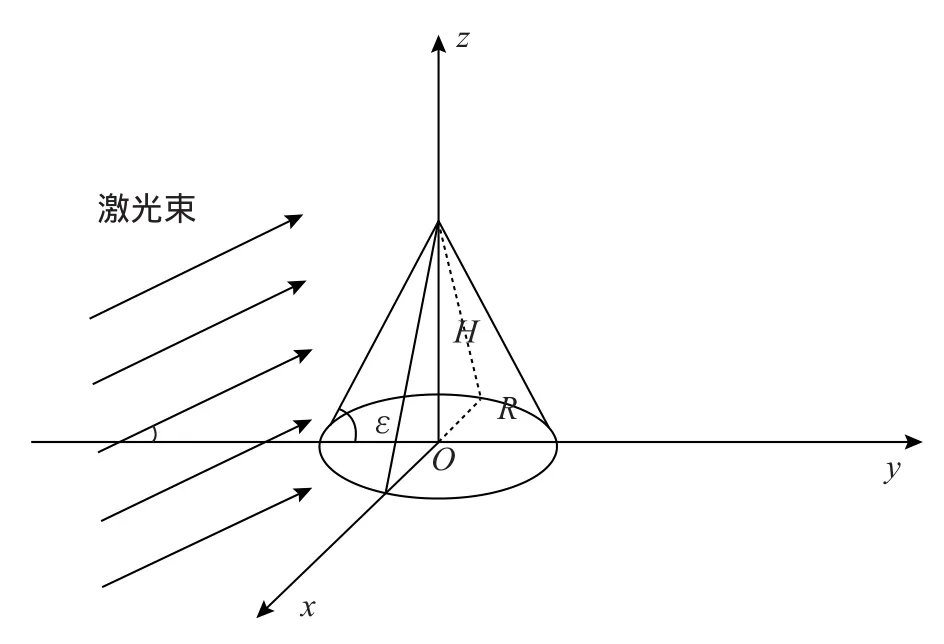
图1 大光斑激光烧蚀圆锥示意图Fig.1 Large spot laser ablation on conical debris

由航天工程大学金星研究员提出的曲面积分理论[4]可知，圆锥体碎片表面面积微元dS受激光烧蚀产生的烧蚀反喷冲量微元dI= (dIx，dIy，dIz)T，满足

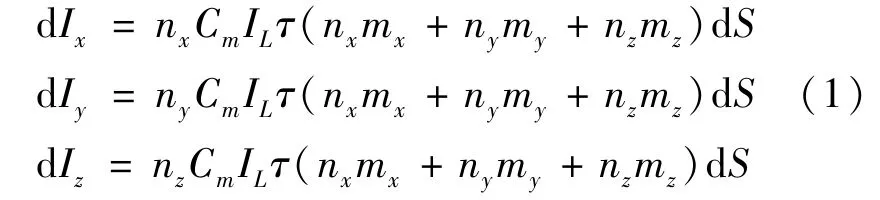
其中，IL为激光功率密度，τ为激光脉宽，Cm为冲量耦合系数，n= (nx，ny，nz) 为dS外法向单位矢量。式 (1)中的积分式属于第一类曲面积分，曲面S在Oxy平面上的投影域为Ω，若单值连续函数z=z(x，y)在Ω上有连续的一阶偏导数，则函数f(x，y，z)在曲面S上的积分满足

单次脉冲激光作用时间为τ′，则单脉冲激光烧蚀力F=(Fx，Fy，Fz)T满足

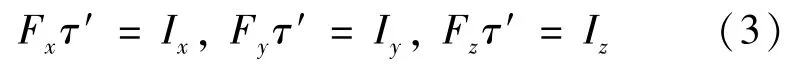
对于圆锥体碎片质心的冲量矩微元为dLI=(dLIx，dLIy，dLIz)T，满足

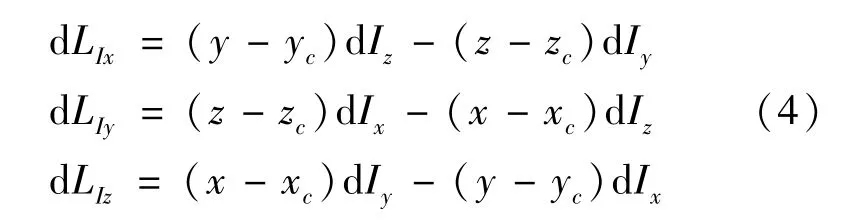
面积微元dS受单次脉冲激光烧蚀产生的力矩dLF= (dLFx，dLFy，dLFz)T，满足

根据激光烧蚀判定原理[4]，若圆锥体表面点(x，y，z)处附近面积微元dS的外法向单位向量n与激光方向单位矢量m的夹角满足(m，n)＞π/2，则此面积微元受激光烧蚀作用，此时m·n＜0。

故由圆锥体表面受不同仰角θ激光照射受辐照区域的不同，可以分为图2中四种情形讨论:

当-π/2≤θ＜-ε，即激光入射角度在区域Ⅰ范围中时，激光烧蚀范围为整个圆锥体上表面曲面S1，在Oxy平面上的投影区域为底面圆S2。

当-ε≤θ≤0，即激光入射角度在区域Ⅱ范围中时，激光烧蚀范围为圆锥体上表面曲面S1上满足y≤0的部分以及满足y＞0、γ＞γ0的部分，其中γ是定义圆锥体上表面曲面S1上满足y＞0的点 (x，y，z)的函数

图2 大光斑激光烧蚀圆锥分区域示意图Fig.2 Interval partition of large spot laser ablation on conical debris

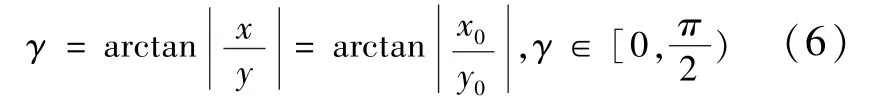
γ0为与圆锥体高径比tanε、激光入射角度θ相关的定值

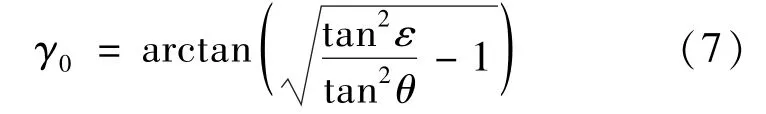
当0＜θ≤ε，即激光入射角度在区域Ⅲ范围中时，激光烧蚀范围为圆锥体上表面曲面S1上满足y＜0、γ＜γ0的部分和底面S2，S1被烧蚀区域在Oxy平面上的投影区域如图3所示。

当ε＜θ≤π/2，即激光入射角度在区域Ⅳ范围中时，激光烧蚀范围为圆锥体底面S2。

3 激光烧蚀力与力矩的计算

由式(1)-(5)，可计算出不同角度入射激光烧蚀圆锥体产生的烧蚀力与烧蚀力矩如下。

激光仰角θ满足-π/2≤θ＜-ε时，烧蚀力大小F积分计算得到

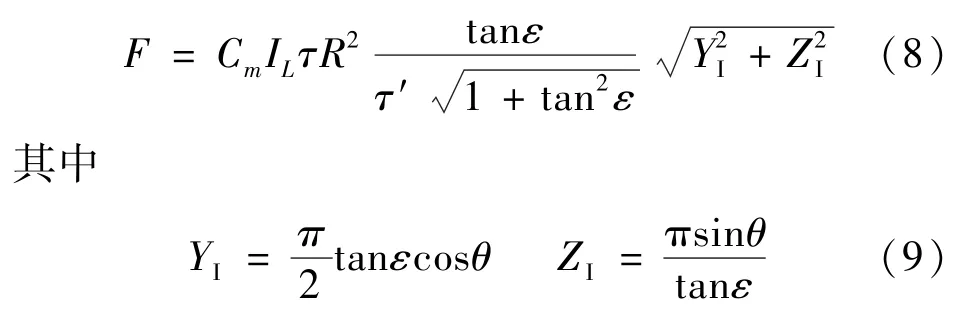
由于-π/2≤θ＜ -ε，即Fy≥0，Fz＜0，可知烧蚀力方向与y轴正方向成夹角θF∈ [-π/2，0]且满足

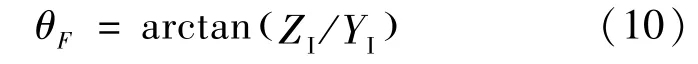
力矩大小LF计算得到

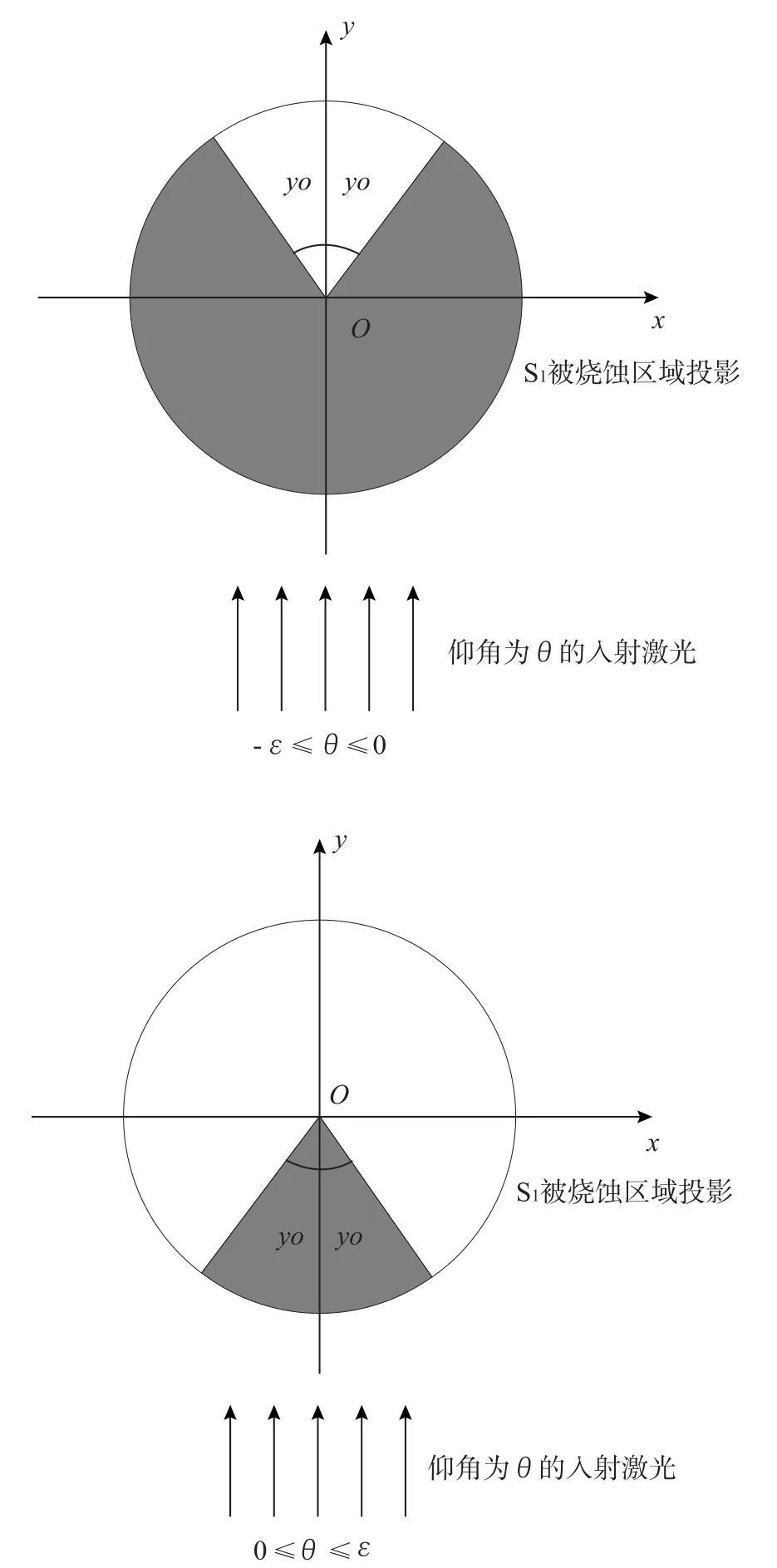
图3 θ∈ [-ε,ε]时圆锥上表面曲面S1上被激光烧蚀区域底面投影示意图Fig.3 The projection of the ablated portion of surface S1on surface S2when θ∈ [-ε, ε]

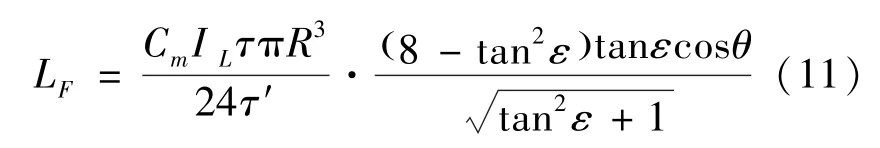
力矩方向沿x轴，正负号表示方向沿着x轴正负方向。

激光仰角θ满足-ε≤θ≤0时，烧蚀力大小F积分计算得到

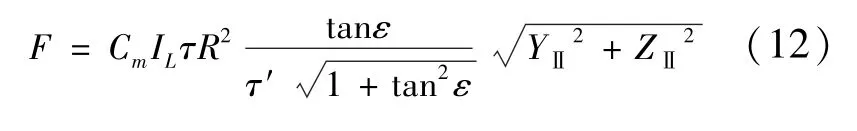
其中

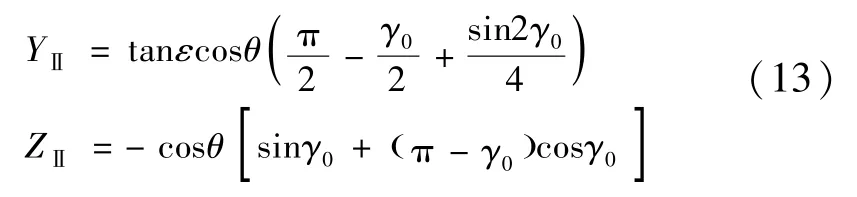
由于-ε≤θ≤0，则Fy＞0，Fz＜0，可知烧蚀力方向与y轴正方向成夹角θF∈ (-π/2，0)且满足

力矩大小计算得到

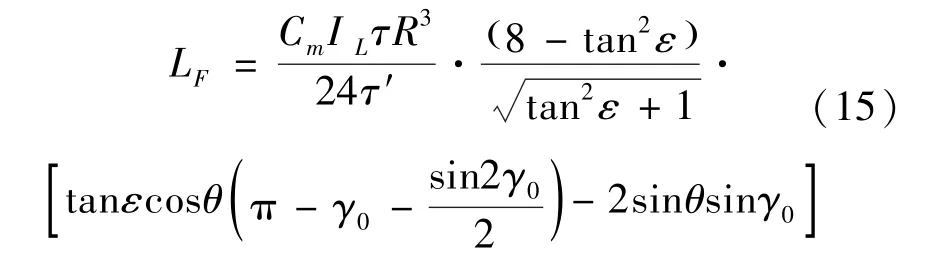
力矩方向沿x轴，正负号表示方向沿着x轴正负方向。

激光仰角θ满足0＜θ≤ε时，烧蚀力大小F积分计算得到

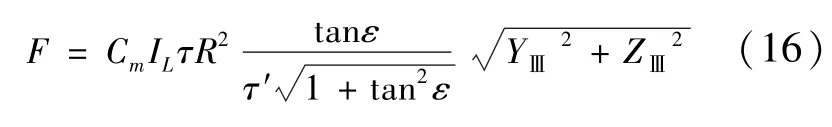
其中

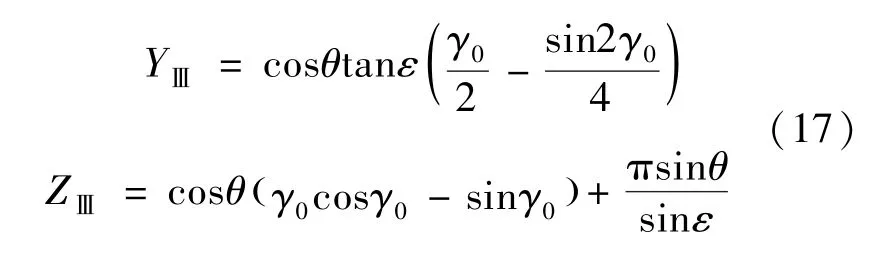
由于-ε≤θ＜0，可验证得到Fy≥0，可知烧蚀力方向与y轴成夹角θF∈ (-π/2，π/2) 且满足

力矩大小计算得到

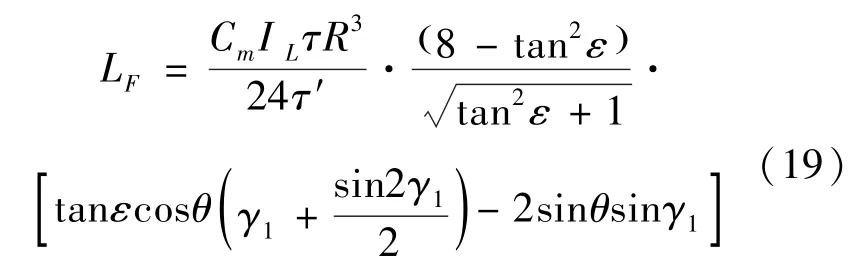
力矩方向沿x轴，正负号表示方向沿着x轴正负方向。

激光仰角θ满足ε＜θ≤π/2时，烧蚀力大小F积分计算得到

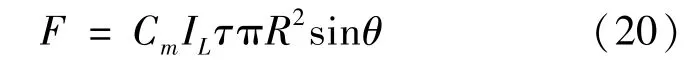
方向沿着z轴正方向。

力矩计算得到可以看出，当激光仰角θ满足ε＜θ≤π/2时，即激光仅烧蚀圆锥体碎片底面部分时不产生烧蚀力矩。

4 计算分析

4.1 激光烧蚀力分析

用F1=CmFLτπR2/τ′对烧蚀力大小F进行无量纲化处理，有

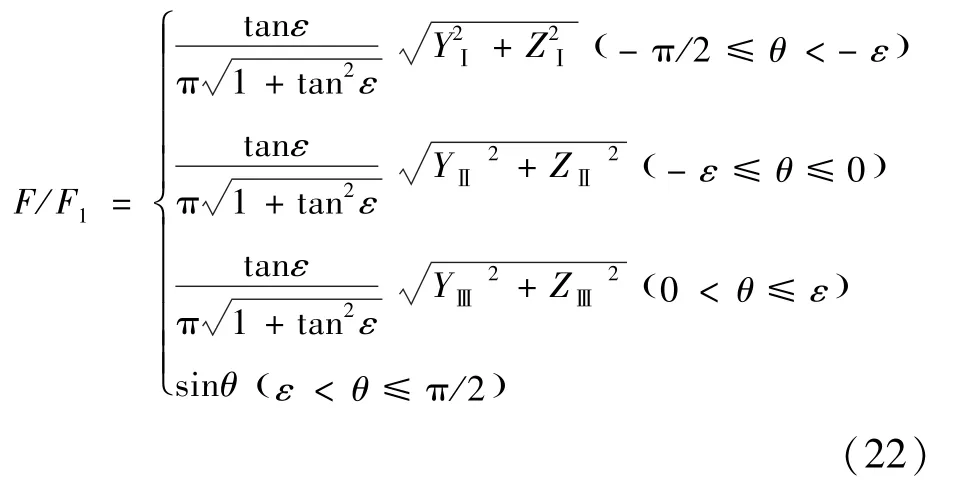
仰角为θ的激光烧蚀圆锥体碎片产生的烧蚀力仰角θF可表示为式 (23)所示的分段函数

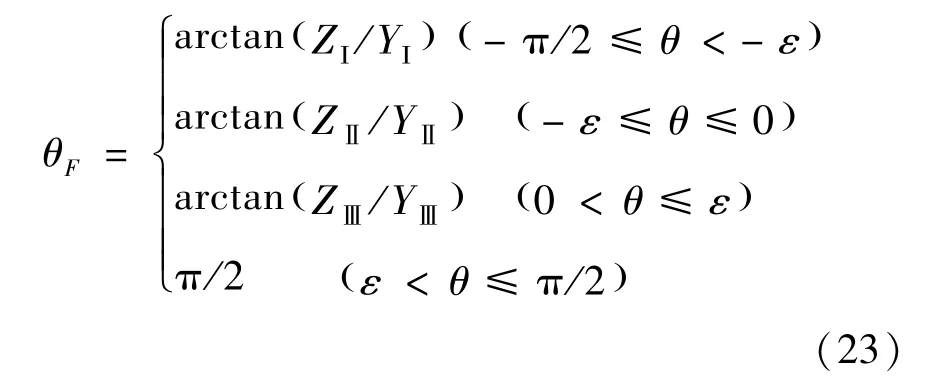
选取高径比H/R为1/4、1/2、1、、2、4和8七种圆锥体作为研究对象，绘制出烧蚀力大小无量纲量F/F1、烧蚀力仰角θF随着激光仰角θ的变化关系图。

图4 7种高径比圆锥体F/F1、θF随激光仰角θ变化图Fig.4 F/F1and θFof cones with different H/R varies with θ

7种高径比的圆锥体烧蚀力仰角θF随着激光仰角θ的增加而增加，激光入射仰角θ从-π/2到π/2变化时，烧蚀力仰角θF也从-π/2逐渐增加到π/2。当-π/2≤θ＜-ε时，高径比越大的圆锥烧蚀力仰角θF的增加速度越快；当-ε≤θ＜0时，所有高径比的圆锥烧蚀力仰角θF的增加速度都很平缓；当0≤θ＜ε时，高径比越大的圆锥烧蚀力仰角θF的增加速度反而越慢；当ε≤θ＜π/2时，所有高径比的圆锥激光烧蚀力仰角θF都保持常数值π/2不变。

4.2 激光烧蚀力矩分析

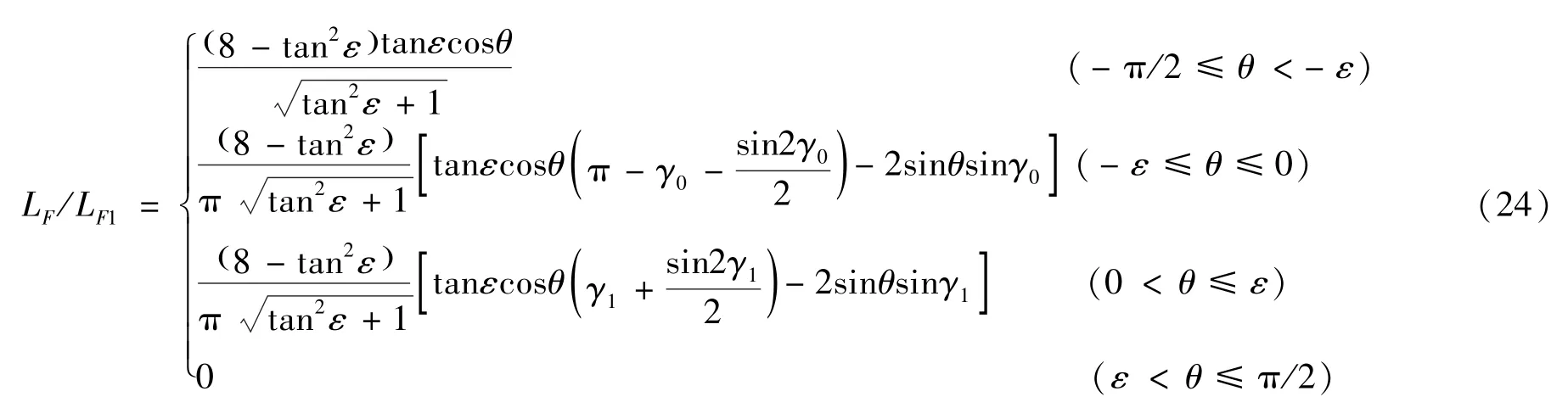
图5 不同高径比圆锥体LF/LF1随激光仰角θ变化图Fig.5 LF/LF1of cones with different H/R varies with θ

5 小结

本文在已有的激光烧蚀理论、曲面积分理论以及激光烧蚀判定原理的基础上，计算出不同角度激光烧蚀圆锥体碎片产生的烧蚀力与烧蚀力矩，给出了以圆锥体高径比、激光入射角度为自变量的函数模型。精确计算出激光烧蚀力与力矩，能为精准安全地清除空间碎片提供数据和理论支持。

选取不同高径比的圆锥体碎片进行研究，绘制出不同角度激光烧蚀圆锥体产生的烧蚀力与力矩图，发现烧蚀力与力矩大小方向与激光入射角度、圆锥高径比的关系具有良好的规律性。