孟德尔遗传定律中2种分离比的2个认识误区

王 彬 刘丽丽 吴效芳

（山东东营市河口区第一中学 山东东营 257200）

孟德尔分离定律和自由组合定律是遗传学的两大基本定律。在发现两大定律的过程中，孟德尔首先进行的是豌豆1 对相对性状的杂交实验，实验中 F1自交，F2出现了“3∶1”的分离比。在此基础上，孟德尔又进行了2 对相对性状的杂交实验，实验中 F1自交，F2出现了“9∶3∶3∶1”的分离比。以上2个分离比是两大遗传定律的特征性数值，在实际应用中具有十分重要的作用。但是，很多教师、很多资料在对这2 个比值的应用总结中出现了想当然的思维误区，现将2 个典型的误区总结如下。

误区1 一个群体中，若1 对相对性状甲与乙的比值接近3∶1，则甲是显性性状，乙为隐性性状

1 对相对性状如何判断其显、隐性？ 这是实际生活中经常面临的问题。上述孟德尔1 对相对性状的杂交实验中，F1自交，F2出现“3∶1”的分离比，其中的“3”恰好对应的是显性性状，“1”对应隐性性状。这可能是作出误区1 推断的主要原因。然而事实都是如此吗？ 请看例1。

例1，一个随机交配的群体，有1 对相对性状甲和乙，它们的数量之比为甲∶乙=3∶1，则甲不一定是显性性状。

分析：假设甲为隐性性状，由a 基因控制，乙为显性性状，由A 基因控制。在亲代群体中，设a的基因频率为 χ，则 A 的基因频率为（1-χ），由于雌、雄配子的结合是随机的，则子代3 种基因型频率分布如表1。

表1 种群随机交配一代后子代各基因型频率

误区2 2 对相对性状的杂交实验中，若出现9∶3∶3∶1 的比值，则这 2 对性状的遗传符合自由组合定律，且决定这2 对相对性状的2 对等位基因位于2 对同源染色体上

人教版教材上介绍的孟德尔2 对相对性状的杂交实验中，F1黄圆豌豆自交，F2出现了 9∶3∶3∶1的分离比。这是一个非常重要的比值，在实践中有着广泛的应用，它常用于判断2 对相对性状遗传是否遵循自由组合定律的重要依据。但是，在平时的教学和备考复习中，对这一数值的应用总结出现了不严谨、不科学的推断，上面的误区2 就是典型的例子。在2 对相对性状的杂交实验中，若出现9∶3∶3∶1 的比值，则这 2 对性状的遗传就一定符合自由组合定律，且决定这2 对相对性状的2 对等位基因就一定位于2 对同源染色体上吗？ 事实未必如此。

在连锁基因位置关系的研究中，有2 个重要的概念：重组值与交换值。重组值（重组率）的计算公式如下：

重组是交换的结果，重组率通常代表交换值或交换率。遗传学研究中可根据重组率的大小作为相关基因的相对距离，从而将基因顺序排列定位于染色体上，并绘制出基因图。但由于杂交实验中，可能发生双交换、四交换或更高数目的偶数交换，导致形成的配子依然是非重组型的，这时如果将重组率看作是交换率，后者则被低估，遗传图距自然也随之缩小。这就需要一个校正公式，常用的较简单的公式是Haldane 推导的作图函数（mapping function）：

式中 R 代表重组率，χ 代表交换率，e 是自然对数的底。该公式表示重组率与图距的关系，而图距的单位是1%的交换率。如果知道了R 值，可通过解方程求得χ，当得到一系列χ 值后，可将作图函数绘成曲线（图1）［1-2］。

图1 重组率和图距的关系［1］

以上曲线称作Haldane 曲线。该曲线有以下几个性质：①曲线起始一小段接近直线，斜率接近于1，这意味着重组率可直接看作为图距，重组率是加性的。②在曲线弯曲度较大的区域，重组率就不是加性的了。③标记基因之间的图距很大时，重组率与图距无关，接近或等于 1／2［1］。

介绍了以上知识，还以孟德尔豌豆杂交实验为例，在孟德尔所选取7 对相对性状的杂交实验中，决定7 对相对性状的7 对等位基因并非恰好分布于豌豆的 7 对同源染色体上。1968 年，Lamprecht 基于Haldane 作图函数和曲线的相关知识，发表了豌豆的遗传图（图2，图中仅呈现豌豆单倍体染色体数目）。

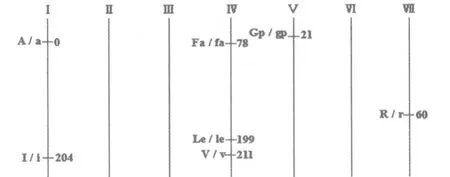
图2 Lamprecht 的豌豆遗传图（Nakazawa，1986）［1，3］

由图2 可知，7 对等位基因只分布在豌豆的4条染色体上。教材上在讲述自由组合定律时，选取子叶的黄和绿（I／i）及豆粒的圆和皱（R／r）这 2 对相对性状的等位基因分别位于Ⅰ号和Ⅶ号染色体上，这2 对性状的遗传当然遵循自由组合定律。但若孟德尔选取的是花冠红色和白色（A／a）与子叶黄色和绿色（I／i）做实验，虽然这 2 对性状的等位基因位于同一条染色体上，但它们之间的图距单位却高达204，应用作图函数推算，重组率竟高达49%，这已经属于自由组合的范围了。即用这2 对性状的纯合亲本做实验，F1自交，F2也会出现接近9∶3∶3∶1 的分离比。同样，若孟德尔研究的是Ⅳ号染色体上的 Le／le（植株的高和矮）或 V／v（豆荚饱满和不饱满）和Fa／fa（花腋生和顶生）之间的杂交组合实验，由于遗传图距较大，也足以获得与自由组合无明显差异的比数［1，3］。

通过以上分析可看出，2 对相对性状的杂交实验中，若出现 9∶3∶3∶1 的比值，则这 2 对性状的遗传表现出了自由组合现象，决定这2 对相对性状的2 对等位基因可能位于2 对同源染色体上，也可能位于1 对同源染色体上。在高中生物学范围内，在不考虑交叉互换的情况下，由“9∶3∶3∶1”的条件才能推出“2 对等位基因位于2 对同源染色体上”的结果。

综合以上，教师在平时的教学和备考复习中，在对生物学规律进行总结和拓展时一定要注意学科知识的严谨性和科学性，要明确这一规律的适用范围及例外性现象。只有这样，才不致于出现绝对化的总结，才能引导学生建立准确、完整的知识结构。