基于可拓理论的山区铁路枢纽土质高陡边坡稳定性评价
邱钰峻 但鹏飞 郭 斌
(1.西南交通大学土木工程学院 四川成都 610032;2.中铁十八局集团有限公司 天津 300222)
1 引言
我国地形西高东低,山区面积占国土面积的三分之二,西部山区铁路路网严重不足。自“十三五”以来,为了缓解不均衡的区域布局,我国铁道部门正不断扩大西部山区铁路网规模并完善我国路网规模[1]。在此过程之中,将不可避免地修建大量山区铁路枢纽,如重庆西站、贵阳北站、溆浦南站等。
西南山区地形起伏大,地质构造复杂,地壳活动强烈,土质高陡边坡极为常见。土质高陡边坡坡体具有脆弱性与不稳定性,在枢纽修筑与运营过程之中,常常由于人为活动的原因,产生崩塌、滑坡等地质灾害,危及施工与运营安全。铁路枢纽作为铁路线网建设的重要节点,在协调不同线路的顺畅衔接利用、实现大量客流及货流和车流的集散与中转等方面都起着至关重要的作用,一旦受到地质灾害的影响,除了枢纽自身的破坏以外,还会阻断关联线路的正常运营,甚至导致区域交通崩溃,造成巨大的经济损失。由此可见,研究如何对铁路枢纽高陡土质边坡进行稳定性评价以指导高陡边坡防护,具有极大的实际意义。
土质高陡边坡是一个受多种因素影响、不确定性大且极为脆弱的动态系统[2-3]。出于土体的复杂性和不确定性,许多因素无法准确获得,只能定性表示,这种定性与定量信息共存的情况必然会对土质高陡边坡稳定性评价结果的合理性产生不利影响。近年来,国内外学者开始引入一些新的理论与方法应对定性与定量信息共存的情况,并取得了一定成果,如粗糙集理论[4]、可拓理论[5]、神经网络[6]等。其中,可拓理论具有能高效处理定性、定量信息并存问题的优点[7],已在决策支持、故障检测、灾害评估等领域得到了应用。因此,本文引入可拓理论展开对铁路枢纽土质高陡边坡稳定性评价的研究。
2 模型构建
2.1 边坡稳定评价指标体系
稳定评价指标作为反映影响边坡稳定性的主要因素,其选择和确定是整个评价体系的基础。本文通过分析大量山区铁路土质高陡边坡技术经济资料,结合专家意见,选择地形地貌V1、地质条件V2、气候水文V3和地震V4四个一级指标,一级指标包含数个二级指标,如图1所示。

图1 特征属性
2.2 指标权值的确定
2.2.1 基于OWA算子的赋权方法基本原理
边坡稳定影响指标的权值反映了不同因素对边坡稳定性的影响程度,因此确定不同指标的权重是进行边坡稳定性评价的第一步。
目前常用的赋权方法(德尔菲法、层次分析法等)大多依据专家的主观判断对不同指标的重要程度进行打分,其过程中不可避免地由于专家的主观偏好产生极值。若不对极值进行处理,势必会影响权重的公正性。针对该问题,本文基于OWA(Ordered weighted averaging)算子来计算土质高陡边坡稳定影响指标权重。OWA算子是一种群集结方法,可用于定量表示因素间相互影响,将其引入与权重计算可降低由专家主观原因产生的极值对结果的影响,可使结果更合理、客观[8]。
利用OWA算子计算权重的步骤如下:
(1)专家打分
由n名专家对边坡稳定影响指标Xi的重要性进行打分,可得各指标分值(x1,x2,…,xn)。将所得分值按小到大排列,并从1开始进行编号,得到分值组 y1≤y2≤…≤yk≤…≤yn。
(2)位置赋权
根据排列组合数对各评价指标Xi分值组(y1,y2,…,yn)赋权,得到权向量 αk:

其中,根据二项式定理:
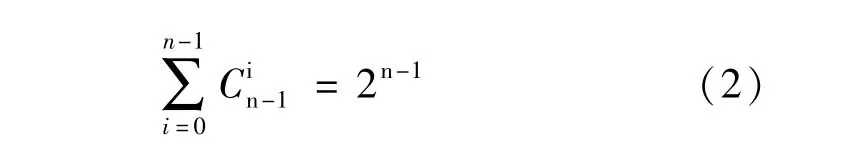
(3)确定绝对权重
利用权向量 αk对分值组(y1,y2,…,yn)加权,得到边坡稳定影响指标Xi的绝对权值w′i:

(4)确定相对权值
根据指标Xi绝对权值w′i其相对权值wi:

根据以上步骤,可得各边坡稳定影响指标权重。
2.2.2 权值计算
本文的研究共咨询了五位专家对边坡稳定性影响因素重要程度进行打分。为了保证打分结果的规范与统一,令分值取值范围为0~10,且是0.5的整倍数,分值越高则说明该专家认为该指标越重要,打分结果见表1。

表1 各特征属性得分结果
由公式(1)和(2),计算得各评价指标绝对权值:w′1=5.875、w′2= 6.625、w′3= 8.125,w′4= 9.094、w′5=5.156、w′6= 6.500、w′7= 4.656、w′8= 5.156。 根据式(3)求得各指标权值见表2,其中一级指标权值为二级指标权值之和。
2.3 标准化处理
本文通过理论分析并结合前人研究成果[9-11],将不同工况下的土质高陡边坡稳定程度分为稳定、较稳定、基本稳定、较不稳定、不稳定五个等级。若指标实际值大于表中最大范围时,按值域范围最大值选取。各工况条件如表3所示。为了避免不同指标量纲对评价的影响,应把各指标数值进行标准化处理。对于指标值越大对边坡稳定性越有利的指标,标准化公式为:
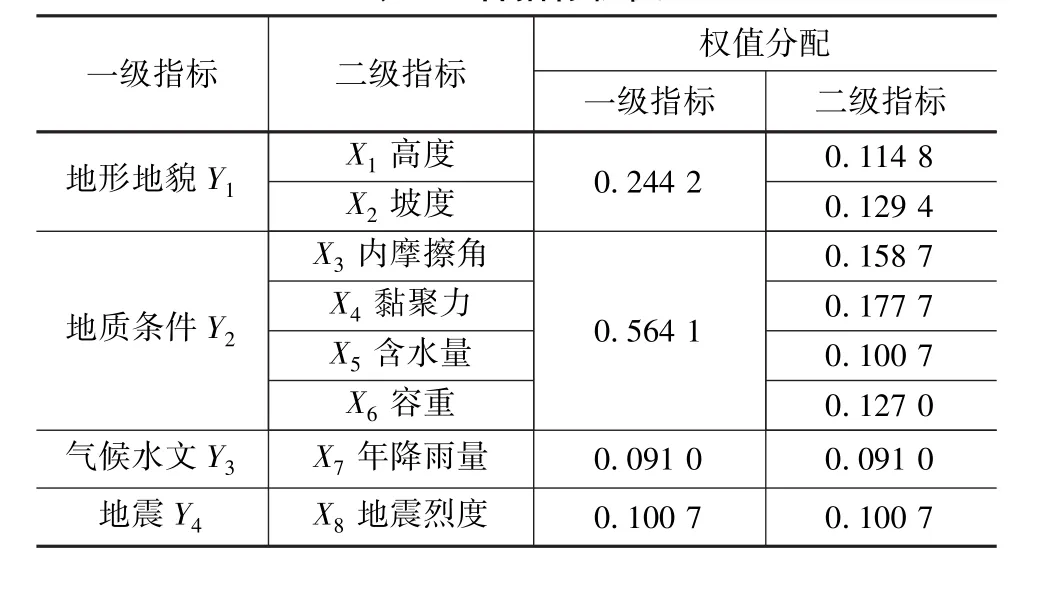
表2 各指标权值

对于指标越大对边坡稳定性越不利的指标,标准化公式为:

式中,qij为标准化处理后的指标值;pij为指标原始值;maxpij和minpij分别为其最大和最小值。
根据式(5)和式(6),对表3中的等级量值范围进行标准化处理,得到表4。
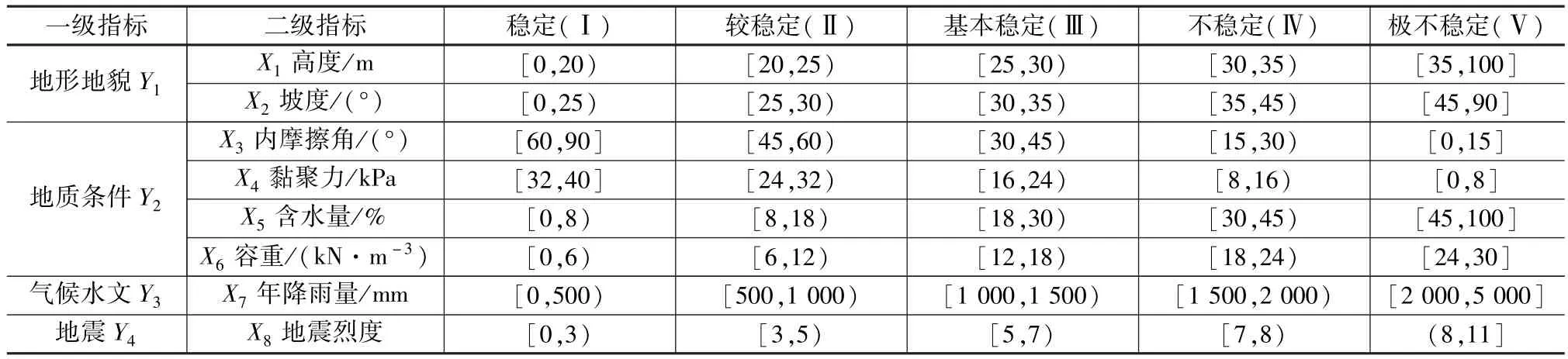
表3 _指标等级量值

表4 _评价指标的等级量值范围(无量纲)
2.4 可拓评价
可拓理论是最早由蔡文提出的新方法,用以解决各种矛盾问题。将物元作为其基本逻辑,以个体名称N、特征C以及特征值V作为基本因素,并用R={N,C,V}描述事物个体[12]。为了减少信息不确定性对土质边坡评价结果的干扰,确保评价准确性,本文采用依次进行二级指标和一级指标的可拓评价的两层可拓评价,得到边坡稳定性评价结果。
2.4.1 二级指标的可拓评价
(1)经典域、节域:依照本文上述评价标准,本文将土质高陡边坡稳定性分为d个等级(d=1,2,…,e),其经典域和节域可表示为
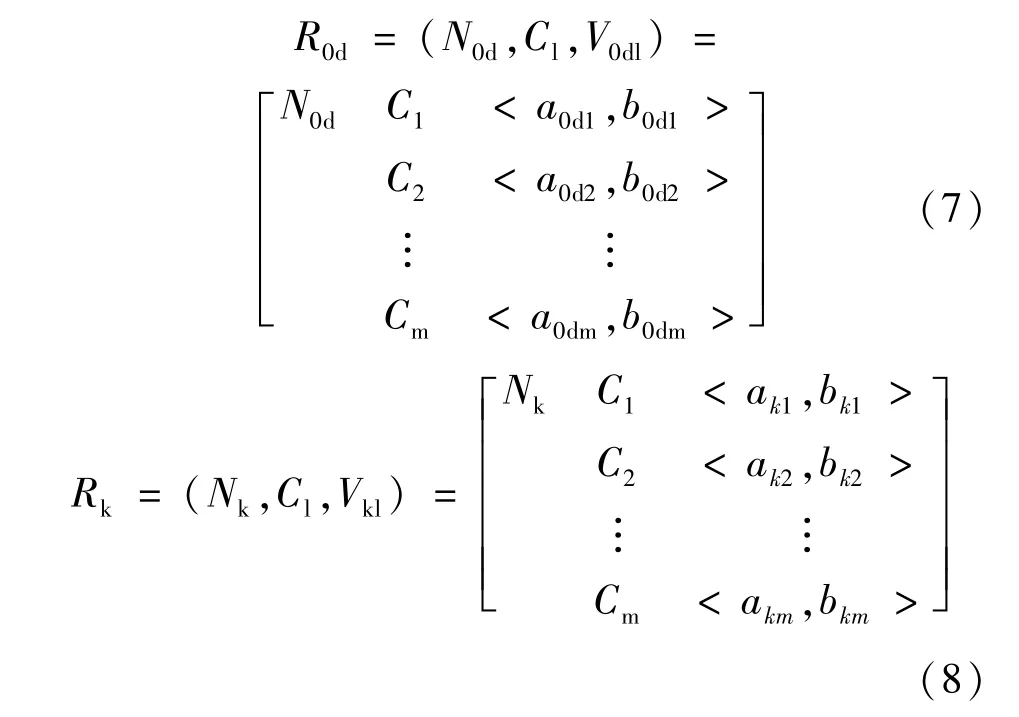
式中,R0d为经典域;N0d为稳定性等级;Cl为各土质边坡稳定性评价指标;V0dl=<a0dl,b0dl>为对应等级的评价指标量值范围;Rk为节域;Nk为边坡个体;Vkl=<akl,bkl>为评价指标等级量值范围的最小值到最大值,即 < a0dl,b0dl> ⊂ < akl,bkl> (l=1,2,…,n)。
(2)待评价土质边坡:根据表4得到待评价土质边坡Ni关于指标Ci的值Vi,边坡 Ni的表示方式为

(3)单指标相关度:为表征同类中不同事物间的差异,在可拓理论中,规定 x0为区间长度,以ρ(x,x0)为距表示x与区间x0=[a,b]之间的距离

单指标相关度,即土质边坡Ni第i个评价指标与等级s的相关性函数为:

(4)综合相关度和等级相关度:待评价土质边坡Ni与等级s的综合相关度为

式中,wi为各指标权重,满足
此外,为了便于比较及消除评价指标量值范围的不对等所造成的影响,需要将us(N)进行标准化处理得到等级相关度:


2.4.2 一级指标的可拓评价
将二级指标可拓评价所得到的等级特征值d作为进行一级指标可拓评价的取值。一级指标的稳定性等级仍为d个,取值范围均匀划为:(1,2),(2,3),…,(d,d +1),若指标值超出范围,则取最大值。其余计算与二级指标评价步骤相同。得出一级指标计算单指标相关度、综合相关度及等级相关度后,便可确定边坡的稳定性。
3 实例应用
3.1 工程概况
该边坡高程300~380 m,自然坡度约25°~46°,局部较陡。滑坡所处地区为丘陵地貌,地表覆盖层主要为第四系全新统冲积层的粗圆烁土、砂质黄土、块石土以及第四系上更新统的风积砂质黄土,厚度为15~20 m。根据现场试验与观察,坡体上部土体结构松散,植被发育,有利于地表水向地下水下渗补给,坡体土含水量为18.77%,内摩擦角约为12°,黏聚力约为8 kPa,土体重度为24 kN/m3。重庆地区属亚热带季风气候,年均温约18℃,年降雨量大于1 000 mm。重庆西站位于中国重庆市沙坪坝区,该地区抗震设防烈度为6度,设计基本地震加速度值为0.05 g。根据表3和式(5)、式(6),得到该土质边坡各评价指标值,见表5。

表5 边坡稳定性评价指标取值
3.2 二级指标可拓评价
利用表4和表5中的评价指标值和表3中各指标权值及式(7)~式(11),可得二级指标的单指标相关度、综合相关度、等级相关度及一级指标值,见表6。

表6 _二级指标可拓评价结果
3.3 一级指标可拓评价
由以上计算可得,地形地貌V1、地质条件V2、气象水文V3及地震V4的一级评价指标值分别为3.389、4.371、2.661和3.155。依照前文所定标准,将一级指标评价中的土质边坡稳定性分为5个等级,取值范围分别是[1,2),[2,3),[3,4),[4,5),[5,6]。其余步骤与二级指标评价的步骤一致,由此可得出该土质边坡一级指标的单指标相关度、综合相关度和等级相关度,见表7。
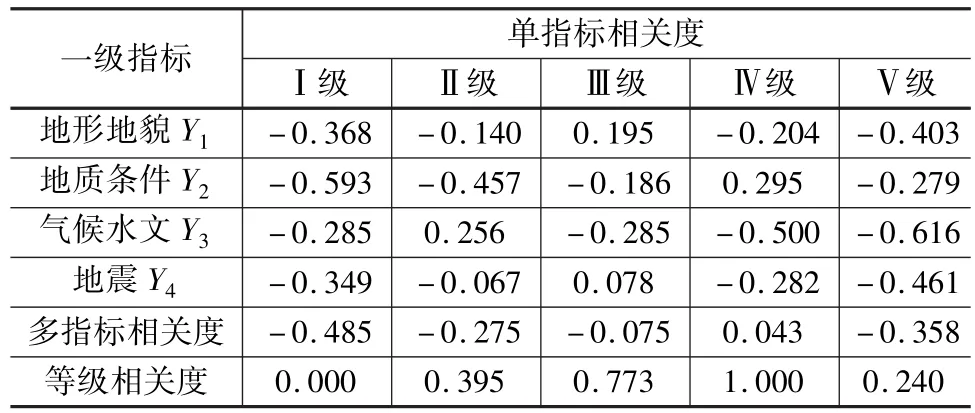
表7 一级指标可拓评价结果
从表7可得,该土质边坡稳定程度与Ⅳ级相关度最大,即该边坡稳定等级处于Ⅳ级,为不稳定状态,这与现场由专家根据有限元法和赤平投影分析法得到该边坡处于极限平衡状态的结果相吻合。
4 结论
本文基于可拓学对铁路枢纽土质高陡边坡稳定性评价模型的研究,得到了以下结论:
(1)考虑地形地貌、地质条件、水文和地震4个方面的因素,选定土质高陡边坡稳定性评价的8个指标建立评价体系,该指标体系可以较好地描述土质高陡边坡特征,评价指标体系较为完整。
(2)采用基于OWA算子的赋权方法,计算过程简便,且减少了由于专家偏好导致的极值对结果产生的不利影响,使评价结果更加客观。
(3)将该模型应用至重庆西站扩能改造工程某土质高陡边坡工点的稳定性评价之中,所得结果与有限元法和赤平投影分析法结果吻合,证明了本文提出模型的有效性,可以推广到其他山区铁路枢纽土质高陡边坡工点的稳定性评价之中。

