非均匀刚度弹性边界结构优化设计及实验验证①

杜凯繁，郝 鹏，董曼红，王 博

(1. 大连理工大学 工业装备结构分析国家重点实验室 工程力学系，大连 116023；2. 北京宇航系统工程研究所，北京 100076)

0 引言

运载火箭地面实验加载系统通常采用均匀刚度的弹性边界将轴压弯矩等载荷加载至主承力筒壳结构中。然而，主承力筒壳结构在真实服役状态下载荷边界通常是刚度非均匀的。同一载荷作用下，非均匀刚度弹性边界使得主承力筒壳结构受到非均匀载荷作用，局部载荷较大，而传统的均匀刚度弹性边界使得主承力筒壳结构受到均匀载荷作用，局部载荷较小。因此，传统的均匀刚度弹性边界过低地估计了实验载荷，需要提出一种非均匀刚度弹性边界的结构设计。

面向运载火箭主承力筒壳结构，国内外学者开展大量关于筒壳轴压实验研究[1-6]。王博等[7-8]面向运载火箭主承力筒壳结构开展轴压屈曲实验，验证实验系统的可靠性和数值预测方法的准确性。Bisagni[9]针对筒壳结构轴压失稳实验开展加载方式研究，定量地分析了静态加载与动态加载对轴压筒壳结构的影响程度，该研究对数值仿真具有指导意义。王栋[10]通过研究弹性边界试验方法，即对待测结构施加弹性支撑，在分别获得整体与支撑结构频响后，通过频域子结构解耦方法，去除支撑结构对待测结构的影响，以得到待测结构自由状态频响，进而解决自由悬吊方法进行结构自由状态频响测试难以满足要求的难题。

对于航天领域主承力筒壳结构，国内外学者开展大量优化设计工作[11-20]。郝鹏等[21]针对箭体中典型的网格加筋柱壳结构，提出自适应代理模型优化设计方法，显著提升优化设计效率。王博和郝鹏等[22]提出了针对多级加筋壳的自适应等效策略分层次优化设计方法。该方法的基本思想是将复杂的优化设计问题分解成多个简单的优化设计问题，从而有效降低结构优化设计维度，根本上保证了筒壳结构性能分析的准确性和优化算法的稳定性。针对非均匀轴压载荷，郝鹏等[23]提出网格加筋结构的布局优化设计方法，实现了筒壳结构的同步失效，大幅提高筒壳结构承载效率。

为解决非均匀刚度弹性边界的设计问题，本文开展如下工作：(1)刚度等效指标选取研究，通过对比真实弹性边界与均匀刚度弹性边界情况下主承力筒壳结构的边界响应，获得刚度等效指标；(2)考虑刚度等效指标的非均匀刚度弹性边界优化设计，以刚度等效指标为设计目标，均匀刚度弹性边界桁条分布角度为设计变量，获得非均匀刚度弹性边界结构设计；(3)非均匀刚度弹性边界结构原理性实验，通过对比真实弹性边界与均匀刚度弹性边界情况下主承力筒壳结构的边界响应，验证该优化设计方法的有效性。

1 刚度等效指标选取

为了使得真实弹性边界的刚度与非均匀刚度弹性边界的刚度一致，需要等效刚度指标来定量化描述两者的刚度分布。因此，以主承力筒壳结构边缘处的位移响应来描述两种边界的刚度分布情况。

为获得等效刚度指标，对比分析真实弹性边界与均匀刚度弹性边界的刚度分布情况，算例设置如表1所示。算例筒壳结构的几何参数：直径D=500 mm，高度H=510 mm。材料属性：铝合金2024，T62状态，弹性模量E=72 GPa，泊松比0.31，屈服强度363 MPa，强度极限463 MPa，密度2.8×10-9t/mm3，延伸率0.12。单元采用ABAQUS提供的S4单元(4节点全积分壳单元)。模型节点数为9120，单元数为8968；真实边界部段节点数为9552，单元数为9284。轴压工况载荷F=5.0 kN，弯曲工况载荷M=6250.0 kN·mm，组合工况载荷F=5.0 kN。有限元分析之后，提取主承力筒壳结构距离50 mm上边缘处的节点位移作为主承力筒壳结构的位移响应。如图1所示。

表1 弹性边界设计算例

图1 主承力筒壳结构边缘处的位移响应

通过数值算例分析，得到主承力筒壳结构边缘处的位移响应如图2所示。对于轴压工况，均匀刚度弹性边界对应的轴向位移为一条直线，刚度分布均匀，而真实弹性边界的轴向位移近似为正弦曲线，刚度分布非均匀，故选择轴向位移为刚度等效指标，如图2(a)所示。对于弯曲刚度工况，均匀刚度弹性边界的径向位移呈近似正弦曲线，而真实弹性边界的径向位移较均匀刚度弹性边界有显著的波动，故选择径向位移为刚度等效指标，如图2(b)所示。对于组合载荷工况(轴压+弯曲)，均匀刚度弹性边界与真实弹性边界的轴向位移和径向位移均有显著的不同，故选择轴向位移和径向位移为刚度等效指标，如图2(c)、(d)所示。

综上所述，轴压工况刚度的等效指标为轴向位移；弯曲工况的刚度等效指标为径向位移；组合工况的刚度等效指标为轴向位移、径向位移。

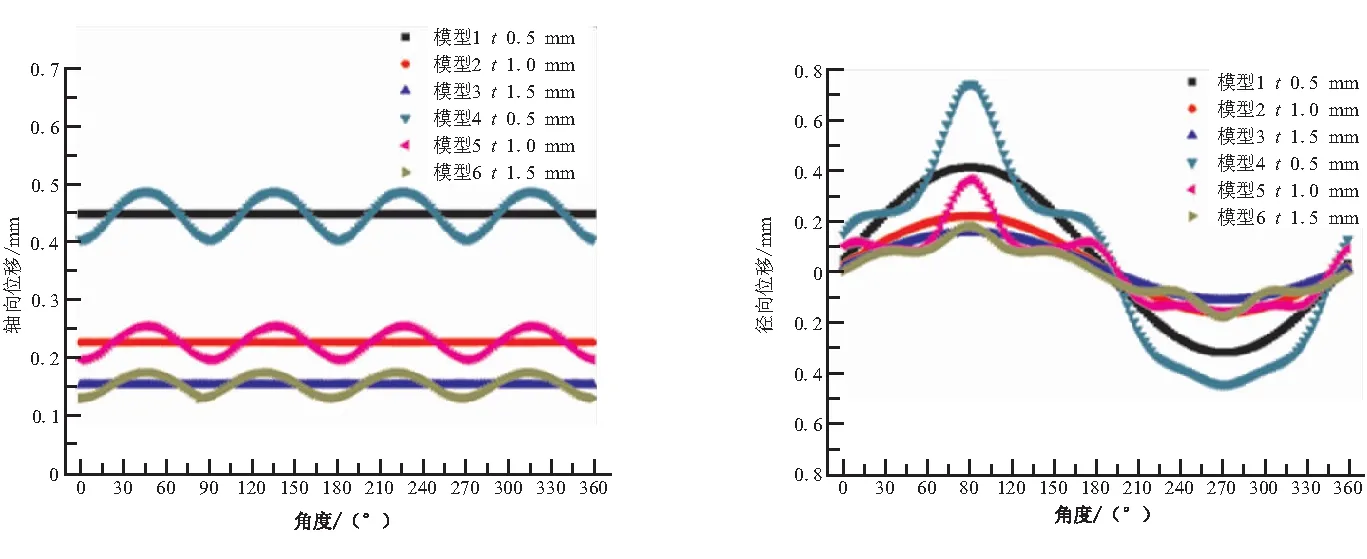
(a)轴压工况轴向位移 (b)弯曲工况径向位移

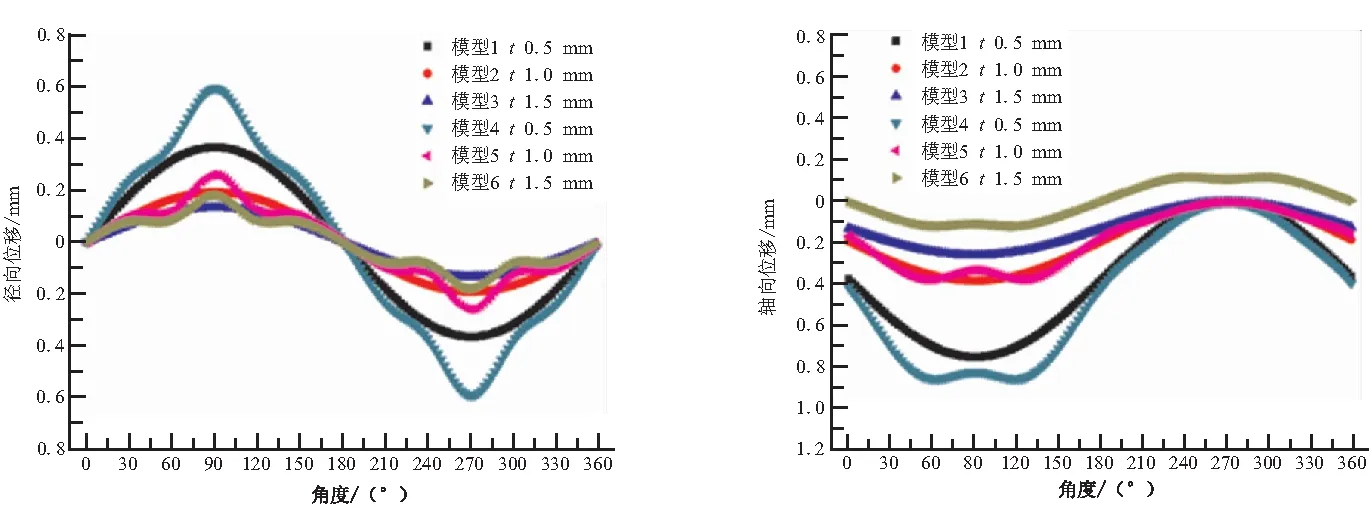
(c)组合工况径向位移 (d)组合工况轴向位移

2 非均匀刚度弹性边界优化设计

基于以上等效刚度指标，建立了非均匀刚度弹性边界结构优化设计列式。以均匀刚度边界的纵向桁条的分布角度为设计变量，以等效刚度指标的均方差最小为设计目标，开展优化设计。当设计目标值趋近于零时，认为非均匀刚度弹性边界与真实的结构边界相一致。此外，根据所得到的等效指标，建立了不同设计目标。优化列式如下：

(1)

式中αi为桁条分布角度；σi为各节点的刚度等效指标的均方差；σ为各节点的刚度等效指标的均方差之和；N为节点数目；n为桁条数目。

为了减少设计变量，提高优化效率，引入式(2)来描述桁条分布角度函数。

(2)

式中L为桁条分布角度之和；nj为桁条数目；λi为分布指数。

因此，设计变量转化λi和nj。为考虑到结构的对称性，L=45°。当λi=1的时候，桁条均匀分布；当λi≠1的时候，桁条呈指数分布，在[0，L]的区间由稀疏到密集。

表2给出了优化设计空间及最优设计。图3给出了均匀刚度边界及设计变量分布。

(a)均匀刚度边界 (b)设计变量分布

轴压工况、弯曲工况和组合工况下，优化设计目标(轴向位移的均方差)最优解分别为0.000 6、0.038 4、0.078 9，说明该优化设计目标与真实弹性边界吻合较好。此外，轴压工况、弯曲工况和组合工况下，优化设计的刚度等效指标的曲线与真实弹性边界的曲线吻合较好(如图4～图6)，说明了提出的优化设计方法及刚度等效指标的有效性。

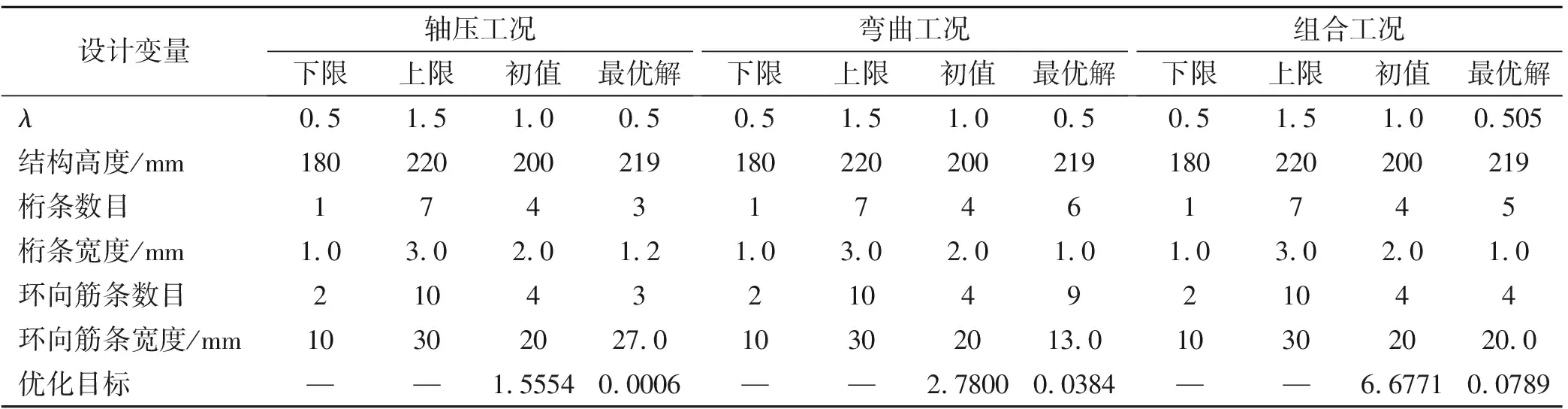
表2 优化设计空间及最优解

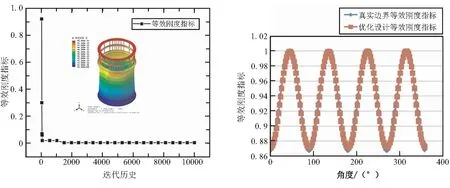
(a)轴压工况迭代曲线 (b)轴压工况轴压位移曲线对比

(a)弯曲工况迭代曲线 (b)弯曲工况径向位移曲线对比

3 非均匀刚度弹性边界原理性实验

为进一步验证非均匀刚度弹性边界结构优化设计方法的有效性，开展非均匀刚度弹性边界优化设计原理性实验。实验思路：通过对比真实边界结构与优化设计得到非均匀刚度弹性边界结构的应力水平，验证该设计方法的可行性。

等效刚度边界设计方法原理性实验的实验试件如图7所示。实验方案由试件，工装和加载器组成。等效刚度边界设计方法原理性实验的实验方案图8所示。实验试件及工装等均采用钢Q235，这是为了便于结构加工制造。考虑到轴压载荷便于实验加载，因此仅验证轴压载荷工况下等效刚度边界工装的传力路径。原理性实验中的轴压载荷为50 kN。

试件A为主承力筒壳结构，结构参数为H=510 mm，R=250 mm，t2=1.0 mm，h1=20 mm，b1=40 mm，t1=3 mm；试件B为真实弹性边界结构，结构参数为H=510 mm，R=250 mm，t2=2.0 mm，h1=20 mm，b1=40 mm，t1=3 mm，开孔尺寸为250 mm×150 mm；试件C为传统的均匀刚度弹性边界结构，试件D为优化设计的非均匀刚度弹性边界结构，参数见表2轴压工况算例初值和优化值。

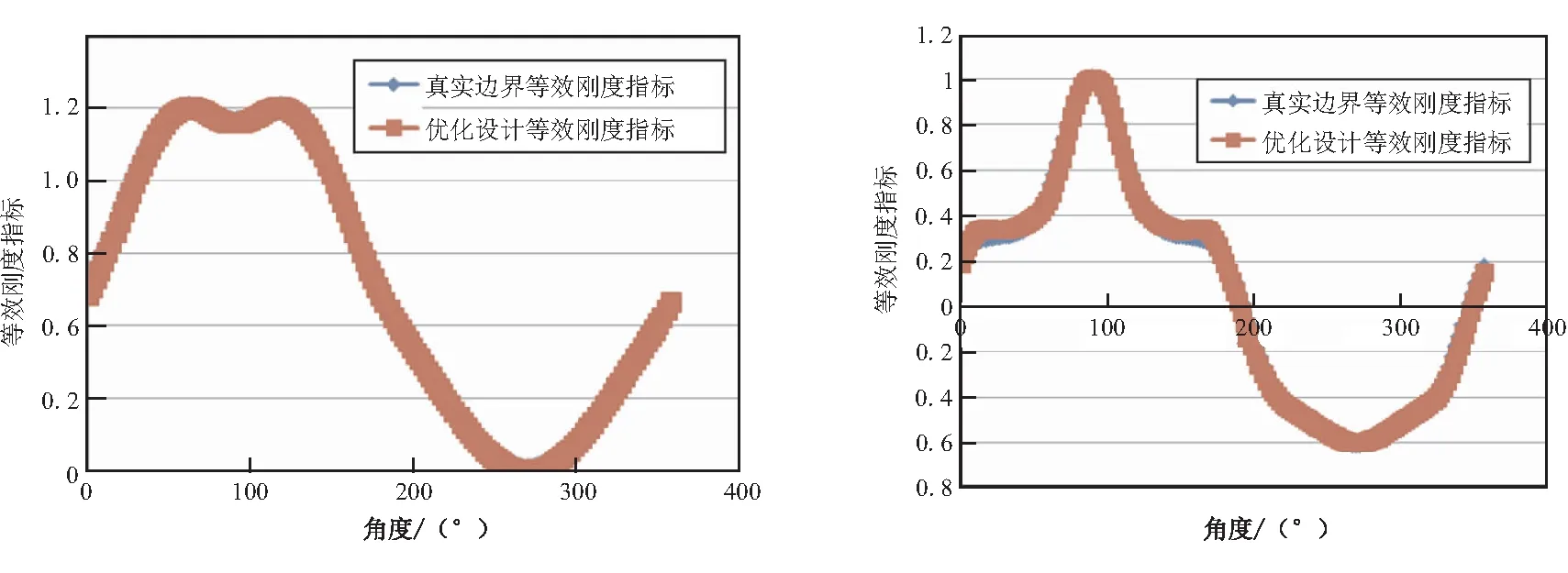
(a)组合工况轴向位移曲线对比 (b)组合工况径向位移曲线对比

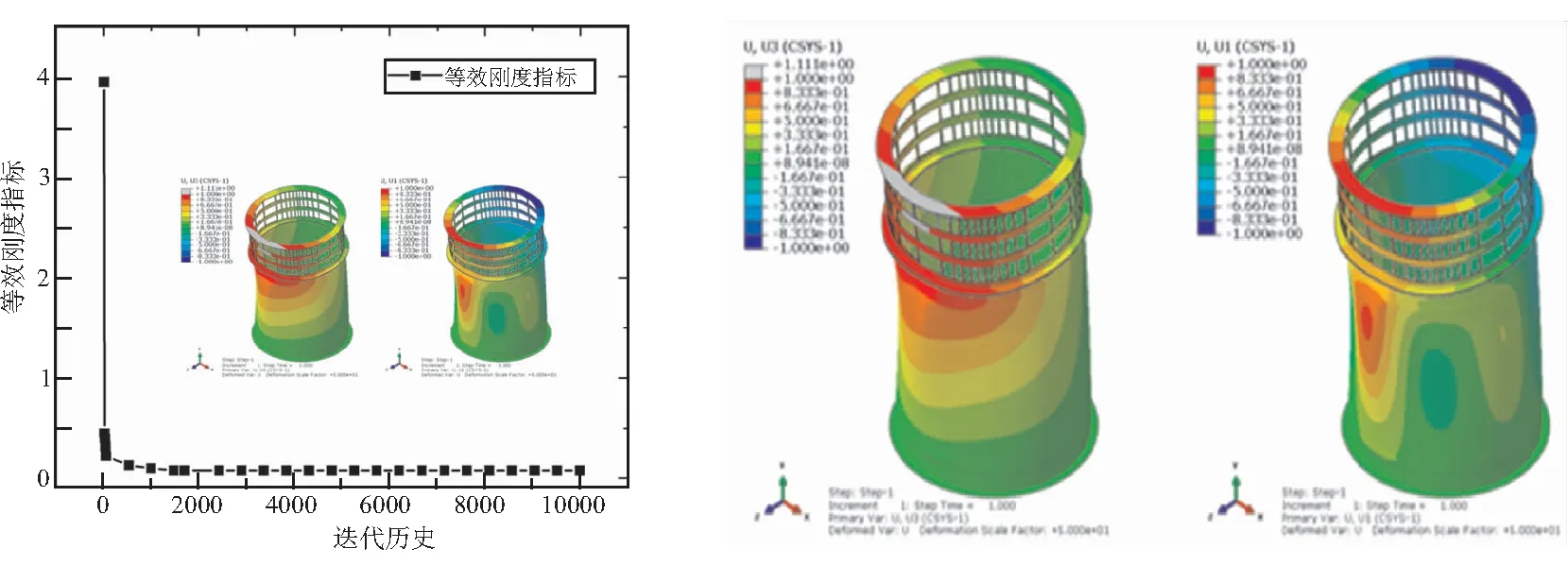
(c)组合工况迭代曲线 (d)轴向位移及径向位移分布

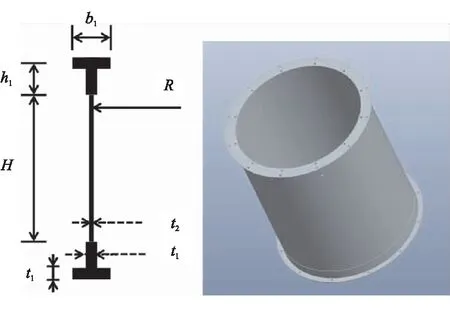
图7 试件结构参数

图9给出了数值预测及实验结果对比，均匀刚度弹性边界(实验1)观测的应力分布较均匀(如Test-1-Single)，而真实弹性边界(实验2)和优化设计弹性边界(实验3)的应力分布相同(如Test-2-Combined和Test-3-Opt)。实验1和实验2的应力分布不相同说明均匀工装和真实边界工装的传力效果不同，应变的平均误差为-22.29%。实验2和实验3的应力分布相同，且平均误差为-13.70%，说明等效刚度边界可以模拟真实边界工装的传力效果。

图8 实验方案

图9(b)给出了数值预测应力分布，该数值预测是模拟真实边界工装的传力路径算例的应力分布。数值预测与实验2的应力分布相同，平均误差为-16.88%，略高于实验2和实验3的平均误差。数值预测与实验结果不同的原因是实验过程中存在不可避免的实验误差，主要为实验蒙皮与端框的焊点不均导致应力分布不均匀，采样点处受到更大的应力值。这也是实验1的应力分布非绝对均匀的原因。

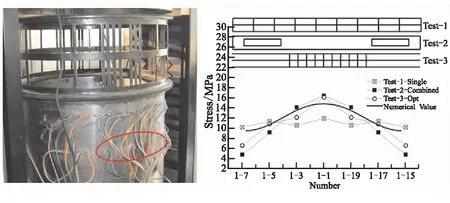
(a)应变片位置 (b)结构应力分布

4 结论

(1)通过开展刚度等效指标研究、考虑刚度等效指标的非均匀刚度弹性边界优化设计研究以及原理性实验研究，提出了非均匀刚度弹性边界结构的优化设计流程，解决了传统均匀刚度弹性边界造成的载荷分配不均匀的问题。

(2)对于航天领域常见的三种工况(轴压工况、弯曲工况和组合工况)，提出了刚度等效指标来描述不同工况下非均匀弹性边界结构的响应，为进一步的优化设计流程提供优化目标。

(3)对于非均匀弹性边界结构优化问题，提出了基于刚度等效指标的非均匀弹性边界结构优化列式。该优化设计列式可以考虑不同载荷工况下的刚度等效指标，实现非均匀刚度弹性边界的优化设计。为提高优化设计效率，提出了引入指数函数来描述桁条分布规律，简化了设计变量，大幅提高了优化设计效率。

(4)为进一步验证非均匀刚度弹性边界结构优化设计方法的有效性，开展了非均匀刚度弹性边界优化设计原理性实验。实验结果显示，优化设计结果与真实弹性边界结果基本一致，验证了等效刚度边界设计方法的有效性。