改进的粒子群BP神经网络算法在天气预测中的应用
沈艺高

摘 要: 介绍了一种基于改进的粒子群算法BP神经网络(IBPPSO)来预测天气情况。粒子群算法BP神经网络(BPPSO)弥补了BP神经网络迭代次数多,运算速度慢的缺点。粒子群算法中学习因子(c1、c2)、惯性权重(w)设定为常数,实际情况下,c1、c2、w随迭代次数而变化。文章对粒子群算法进行适当改进,对最佳位置的搜索从全局的大范围渐渐向局部的小范围转变,既满足了较大的全局搜索能力,又增加了小范围局部搜索的精度。该方法应用于上海虹桥机场近三年来12000组天气情况数据。结果表明,IBPPSO预测准确率和成功预测雨天概率两方面都优于BP神经网络与BPPSO。
关键词: 粒子群算法; BP神经网络; 改进; 天气预测
中图分类号:TP301.6 文献标志码:A 文章编号:1006-8228(2019)08-18-03
Abstract: This paper introduces an improved particle swarm optimization based BP neural network (IBPPSO) to predict weather conditions. The particle swarm optimization BP neural network (BPPSO) makes up for the shortcomings of the traditional BP neural network, which has many iterations and slow operation speed, and enhances the global search ability of the BP neural network algorithm. In particle swarm algorithm, the learning factor (c1、c2) and inertia weight (w) are set as constants. In practice, c1、c2、w vary with the number of iterations. In this paper, the particle swarm algorithm is improved appropriately, and the search for the best location is gradually changed from the global large-scale to the local small-scale, which not only satisfies the larger global search ability, but also increases the precision of the small-scale local search. The method is applied to test 12,000 sets of weather data of Shanghai Hongqiao Airport in the past three years. The results show that IBPPSO is superior to BP neural network and BPPSO in both accuracy and probability of successful prediction of rainy days.
Key words: BP neural network; particle swarm optimization; improved; weather forecast
0 引言
惡劣的天气给人类社会造成的经济,精神上的损失已经不可估量。在环境多变的今天,对天气进行提前预测,进而对一些突发的情况做出准备已经变得至关重要。
从17世纪开始科学家使用科学仪器来测量天气状态,并使用大量的天气数据来预报天气。随着时代的发展,预测天气的方法越来越多。有学者提出将BP神经网络应用于天气预测,却面临着算法迭代次数太多,容易陷入局部极值,全局搜索能力弱等问题。后来有学者提出基于粒子群算法的BP神经网络模型,但仍存在预测精确度低的问题。
本文提出一种基于优化的粒子群算法的BP神经网络模型,改变了粒子群算法常系数的模式,使学习因子及惯性权重随着迭代次数的变化而变化,同时其变化规律满足先全局搜索后局部搜索的思想,既发挥了粒子群算法全局搜索能力强的优点,同时也提高了预测的准确度。
1 算法原理
1.1 粒子群算法
粒子群算法(particleswarm optimization,PSO)最早由Eberhart和Kennedy于1995年提出,它源于对鸟类觅食行为的研究[1]。鸟类在捕食时,为了能够得到更多的食物,会考虑去往以下两个位置:其自身所经历的食物最多的位置及鸟类种群中所普遍认为的食物最多的位置。粒子群算法利用适应度函数来表征每个粒子的优良程度(对应于食物多少的程度),每个粒子同时具有三项特征:速度,位置,适应度。假设在一个n维空间中有m个粒子,则第i个粒子的位置即为:[Xi=(xi1,xi2,...,xin)],第i个粒子的速度即为:[Vi=(vi1,vi2,...,vin)],为了找到拥有最优适应度的位置,粒子群不断迭代进化。在迭代中,每个粒子维护一个其自身的最优位置,称为个体极值[pbest],则对于第i个粒子,其个体极值[pibest=(pi1,pi2,...,pin)];对于整个粒子群,在每次迭代时,需维护一个最优位置,称为全局极值[gbest],记为[gbest=(g1,g2,...,gn)];在迭代过程中,粒子下一时刻的位置取决于其当前位置,当前速度,其个体极值及全局极值,其迭代公式如下[2-3]:
其中,[c1]和[c2]称为学习因子。w称为惯性权重(inertia weight)[4]。
上面的公式分为三部分。第一部分由前一时刻粒子速度决定,体现记忆功能。第二部分粒子参考了自身经历,对下一次移动做出选择,体现其自身的智能性。第三部分粒子结合整个粒子群的共享信息来改变自己的位置增强了粒子的全局搜索能力,体现了粒子间的团结协作[5]。
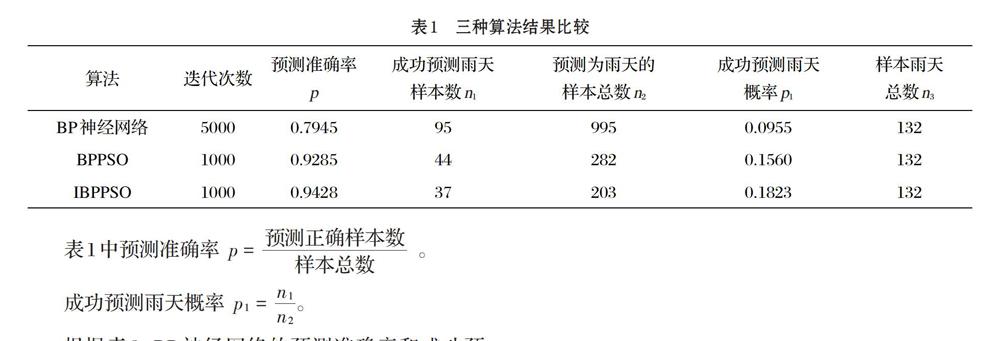
在迭代中,粒子速度应限定在一定范围,即取定一个最大速度[Vmax]和一个最小速度[Vmin],粒子速度满足:[Vmin 粒子群算法具有强大的全局搜索能力,可以避免陷入局部极值。 1.2 BP神经网络 BP神经网络是一种多层前馈神经网络,这是目前应用最广的神经网络。其包含三层:输入层,隐含层,输出层,层与层之间的联系如图1: ⑴ 在信号前向传播阶段,输入信号依次经过输入层,隐藏层,输出层,最后计算得到输出结果。设[Wij(l)]为从[l-1]层第[j]个神经元与第l层第i个神经元之间的连接权重;[bi(l)]为第l层第i个神经元的偏置,[neti(l)]为第l层第i个神经元的输入,[hi(l)]为第l层第i个神经元的输出,则: 其中, [f(x)]为神经网络的激活函数。通常激活函数取非线性函数,因为多层神经网络本质上是多个线性函数叠加,若采用线性激活函数,则其结果仍为一个线性函数。一般来说,我们选择sigmoid函数作为激活函数[6],即: [f(x)=11+e-x]。 ⑵ 在误差反向传播阶段,通过实际输出与真值的差值作为误差,再通过误差的反向传播,逐次调整模型的权重和偏置,直到误差满足要求或达到迭代次数。设共有[n]个样本,则样本的总误差即为[2]: [error=i=1nj=1l(realji-outji)2] ⑸ 其中,[realji]为第j个输出在第i组样本作用下的真实值,[outji]为第j个输出在第i组样本作用下的实际输出值。 BP神经网络简单,易实现,但其收敛速度慢,得到贴合实际的参数需经过大量迭代,而且容易陷入局部极值,偏离全局极值。 2 算法改进 2.1 基于粒子群算法的BP神经网络模型(BPPSO) BP神经网络收敛速度慢,容易陷入局部极值,偏离全局极值,因此,应用粒子群算法,增加参数向目标方向进化的速度,同时增强模型的全局搜索能力,使最终得到的模型更加准确地进行预测。 基于粒子群算法的BP神经网络模型,采用粒子群算法取代反向误差传递来进行对参数的调整,在每次迭代中,将样本的总误差[error]作为粒子群算法的适应度函数,将神经网络的权重[W]及偏置[b]作为粒子的位置,值得注意的是,此时希望误差取极小值,因此算法中寻找的是适应度函数值最小的粒子的位置。算法执行步骤如下。 ⑴ 初始化粒子群的位置(权重及偏置),个体极值[Pbest]及全局极值[gbest]。 ⑵ 进行迭代。根据每个粒子的个体极值[Pbest]和全局极值[gbest]计算粒子的速度,进而更新粒子的位置。根据新的位置分别计算每个粒子所对应的样本总误差作为适应度函数值,再更新每个粒子的个体极值[Pbest]及全局极值[gbest],再进行下一轮迭代。 ⑶ 达到迭代次数,得到最终权重及偏置(全局极值[gbest])。 2.2 基于优化的粒子群算法的BP神经网络模型(IBPPSO) 粒子群算法中学习因子和惯性权重设定为常数,在实际情况下,我们需要[c1],[c2]及w随迭代次数变化,从而实现对最佳位置的搜索从全局的大范围渐渐向局部的小范围转变,既满足了较大的全局搜索能力,又增加了小范围局部搜索的精度。我们根据吕祥铭等人的研究结果[3],调整参数如下: 3 天气预测 作者收集了上海虹桥机场近三年来每日不同时刻的近12000组天气情况数据作为数据集。取其中2000组作为测试数据,剩余近10000组作为训练数据。在训练过程中,提取温度,湿度,气压,风速四个特征作为输入节点,通过神经网络,将样本分为晴天和雨天。模型输入层有4个节点,隐藏层有9个节点,输出层有2个节点。三种算法预测结果如表1所示。 根据表1,BP神经网络的预测准确率和成功预测雨天概率分别为0.7954和0.0955。BPPSO的预测准确率和成功预测雨天概率分别为0.9285和0.1560。IBPPSO的预测准确率和成功预测雨天概率分别为0.9428和0.1823。可以看出,IBPPSO迭代次数优于BP神经网络,同时在预测准确率和成功预测雨天概率两方面都优于另外两者,具有更高的准确度。 4 结束语 本文针对BP神经网络迭代次数多,运算速度慢的缺点,将改进后的粒子群算法应用于BP神经网络来预测天气情况。该方法既满足了粒子群算法较大的全局搜索能力,增加了小范围局部搜索的精度,又提高了算法拟合的准确度及天气预测的准确率,具有一定的推广价值。由于时间原因,本文测算样本量与迭代次数还较少。随着样本量的增加,未来将根据预测情况不断调整学习因子和惯性权重,进一步提高天气预报的准确率。 参考文献(References): [1] 皮倩瑛,叶洪涛.一种动态调节惯性权重的粒子群算法[J].广西科技大学学报,2016.27(3):27-31 [2] 林宇锋,邓洪敏,史兴宇.基于新的改进粒子群算法的BP神经网络在拟合非线性函数中的应用[J].计算机科學,2017.11:51-54 [3] 吕祥铭,闫跃,吕淞霖,张淑颖.基于非线性粒子群算法与神经网络的天气预测[J].现代农业科技,2013.11:265-266 [4] HUANG Hao, CHEN Kui-sheng, ZENG Liang-cai. A genetic algorithm-based neural network approach for fault diagnosis in hydraulic servo-valves[M]//Advances in Machine Learning and Cybernetics.Springer Berlin Heidelberg,2006:813-821 [5] 李松,刘力军.改进粒子群算法优化BP神经网络的短时交通流预测[J].系统工程理论与实践,2012.32(9):2045-2049 [6] 王慧,刘希玉.基于最具影响粒子群优化的BP神经网络训练[J].计算机工程与应用,2007.43(18):69-71

