基于模糊自适应PID 算法的工业机器人运动控制研究

王贵丽 刘伟民 麻丽明 刘小凡 河北机电职业技术学院电气工程系

引言

随着机器人技术的快速发展，机器人在各行业中应用越来越广泛。工业机器人的应用促使传统工业发生新的变革。工业对机器人的需求不仅从数量上大幅度提高，对其性能要求也越来越高，因此需要不断提高机器人的控制精度，满足现代企业对制造能力和效率的高标准要求。

在实际工程应用中，工业机器人具有非线性、耦合性强、数学模型不确定的特点。针对机器人控制的数学模型不确定性，本文把模糊自适应PID 控制算法应用在六自由度关节型机器人ER3A-C60上，通过理论分析和仿真实践，验证所提出的算法能够实现系统的渐进稳定性。

1、 建立ER3A 机器人的运动学模型

本文以ER3A-C60 型机器人为例，基于基坐标变换的4 参数的D-H 模型对工业机器人的运动学模型进行分析。图1 是关节变换原理图及参数。

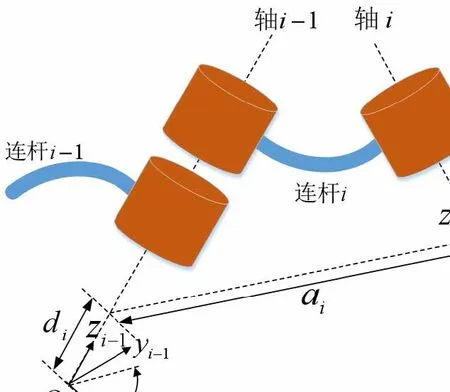
图1 关节变换原理图及参数

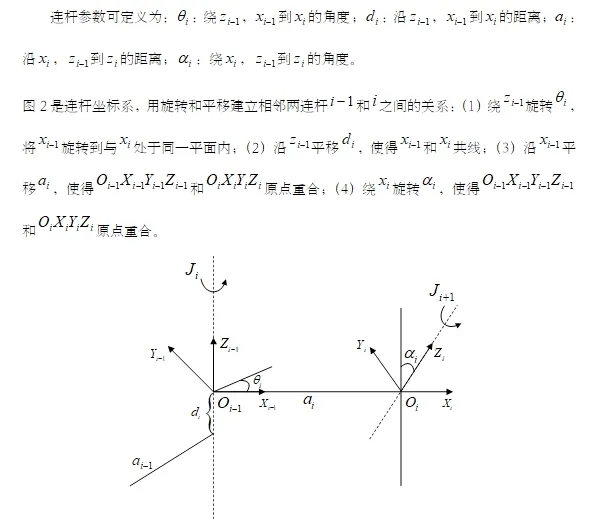
图2 连杆坐标系

对于安徽埃夫特ER3A-C60 型工业机器人，按照标准D-H 建模方法建立如图3 所示的ER3A 机器人D-H 坐标系。

图3 ER3A 机器人D-H 坐标系

根据建立的ER3A 工业机器人D-H 模型可以得到ER3A 的D-H 参数，如表1 所示：

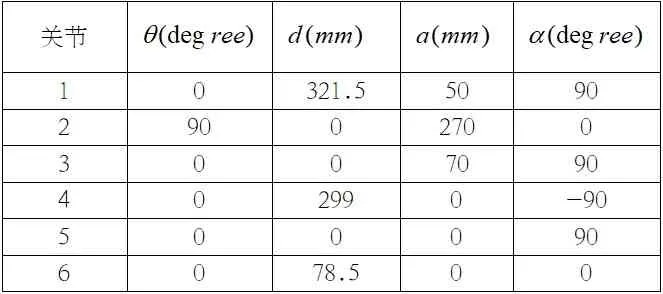
表1 ER3A 机器人D-H 参数表

2、 模糊自适应PID 控制器的设计

2.1 模糊自适应控制算法设计

模糊自适应控制算法目的是在线实时辨识构建ER3A-C60 型机器人的数学模型，并基于该模型设计一种符合期望动态参数的控制器。

假设六自由度机器人数学离散模型如下：

2.2 模糊自适应PID 控制器的设计

传统PID 算法根据系统反馈，对误差进行调节，其数学模型都是将多样性，高耦合性的复杂系统抽象为具体的数学矩阵模型，误差较大。传统机器人采用经典PID算法控制易出现各状态量调节时间长，超调量大，控制精度不高。

图4 模糊自适应控制回路

图4 设计的是模糊自适应控制回路。为降低模型对噪声的感知度，减少噪声对系统的干扰，修正时间参数选取较大的数值，并引入“调整遗忘因子”。

模糊自适应控制算法恰好弥补建模的不足，根据已经建立的数学模型，随机器人运行参数的变化，自适应调整其数学模型。

3、 利用MATLAB 对自适应模型的仿真

3.1 建立系统结构仿真框图

利用MATLAB，搭建出自适应模糊PID 和常规PID 控制系统仿真框图，如图5 和图6 所示。

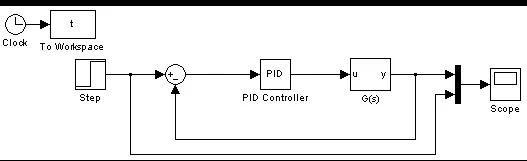
图6 常规PID 控制系统仿真框图

3.2 仿真结果分析

（1）通过MATLAB 数学模型仿真模型框图搭建完成后，运行可得上述两种控制系统的控制曲线图，如图7 和图8 所示。对比发现，模糊自适应PID 调节时间短，控制精度较高。

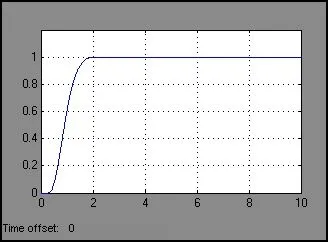
图7 模糊自适应PID 控制曲线图

图8 常规PID 控制曲线图

（2）在仿真的过程中采用Sources 模块库中的Pulse generator(脉冲发生器)作为干扰，加入扰动后的模糊自适应PID控制系统仿真框图和常规PID 控制系统仿真框图分别如图9 和10所示。

图9 加扰动模糊自适应PID 控制系统仿真框图

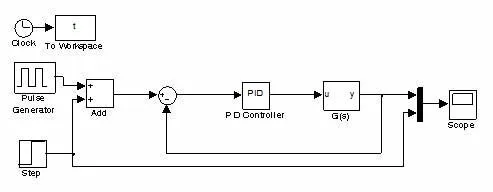
图10 加扰动PID 控制系统仿真框图

对加干扰信号前后分别进行仿真，可得上述两种控制系统的控制曲线图，如图11 和图12 所示。对比发现，加入干扰后，模糊自适应PID 控制系统，调节时间较短，系统更快趋于稳定。

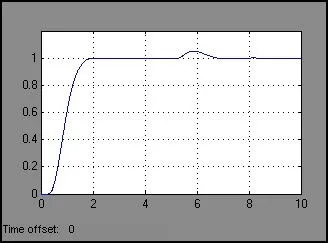
图11 加入干扰后的模糊自适应PID 控制曲线图

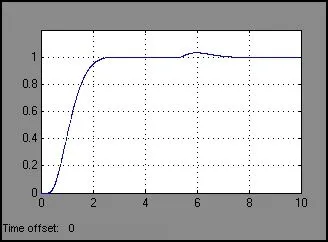
图12 加入干扰后的常规PID 控制曲线图

4、 小结

通过以上仿真结果表明，本文所研究的六自由度关节型机器人ER3A-C60 自适应模糊PID 系统，调节时间短，响应速度快，在实际应用中，验证了有效性和可行性，对工业机器人控制研究有一定的参考价值。