基于连续潮流计算的VSC-MTDC异步互联电网换流站参数优化方法

马任远 汤馨延

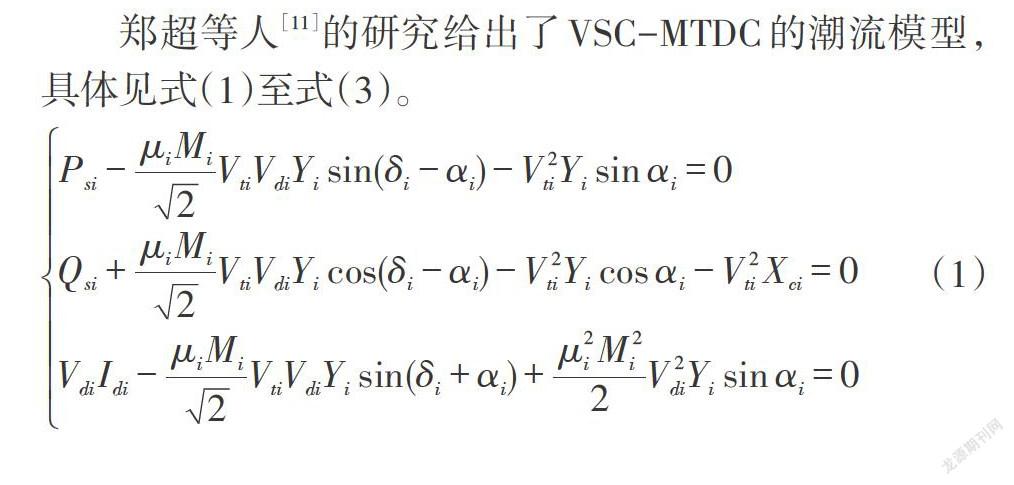
摘 要：针对由多端口柔性直流输电网络（VSC-MTDC）进行连接的异步互联电网，本文提出了一种基于连续潮流计算的换流站整定参数优化方法。该方法以全网静态电压稳定裕度最大化为优化目标，以分区断面传输功率恒定为等式约束条件，以遗传算法为计算核心，对各VSC换流站的整定控制参数进行优化。本文利用IEEE-RTS96仿真系统对所提优化方法进行验证。结果显示，本文所提方法可以在保证分区间传输功率恒定的前提下得到最优的换流站整定控制参数方案，有效提升系统的电压稳定性。

关键词：VSC-MTDC;连续潮流计算;遗传算法;静态电压稳定分析

中图分类号：TM721.1 文献标识码：A 文章编号：1003-5168（2019）28-0126-04

Parameter Optimization Method of VSC-MTDC Asynchronous Interconnected Power Grid Based on Continuous Power Flow Calculation

MA Renyuan1 TANG Xinyan2

（1.State Grid Henan Electric Power Company Economic and Technological Research Institute，Zhengzhou Henan 450052;

2.China Resources Snow Breweries Corporation Chongqing Division，Chongqing 400042）

Abstract： For the asynchronous interconnected power grid connected by multi port VSC-MTDC， this paper presented an optimization method of converter station setting parameters based on continuous power flow calculation. In this method， the optimization target was to maximize the static voltage stability margin of the whole network， the equal constraint condition was to keep the transmission power of the partition section constant， and the genetic algorithm was used as the calculation core to optimize the setting control parameters of each VSC converter station. This paper used IEEE-RTS96 simulation system to verify the proposed optimization method. The results show that the method proposed in this paper can obtain the optimal scheme of converter station setting control parameters under the premise of ensuring the transmission power between the zones is constant， and effectively improve the voltage stability of the system.

Keywords： VSC-MTDC;continuous power flow calculation;genetic algorithm;static voltage stability analysis

1 研究背景

自20世纪70年代以来，国际上多个电力系统相继发生了多起因电压失稳而造成的大规模停电事故[1-5]。目前，电压不稳定风险已经成为电力系统正常运行的最大威胁，因此，对结构日益复杂的现代电力系统进行快速和精确的电压稳定性评估是非常有必要的，且极具社会经济价值。连续潮流方法具有可以追踪节点电压随负荷功率变化的PV曲线、评估结果客观、不存在计算困难等优点，已经成为国内外电力系统中应用最广泛的在线静态电压稳定分析工具。

相对于以电流源换流器（Current Sourced Converter，CSC）为代表的传统晶闸管整流器，电压源型换流器（Voltage Sourced Converter，VSC）具有以下优点[6-8]：①更容易扩展到多端网络;②有功功率和无功功率可以独立控制;③相对于CSC换流器，其直流端电压可以作为一个控制选项;④不存在换相失败的风险;⑤不用花费资金和场地去购置谐波滤波器;⑥建设和试运行时间较少;⑦相对于CSC，VSC更适合可持续新能源的接入。在这种情况下，以多端口柔性直流输电网络（Voltage Sourced Converter based Multi-Terminal DC，VSC-MTDC）进行区域连接的异步互联电网正在世界范围内迅速发展。例如，连接西南电网和华中主网的渝鄂背靠背±420kV柔性直流异步互联系统（2019年6月投运），连接广东、广西和云南电网的乌东德多端口超高压柔直输电工程等。由此可以预见，以多端柔性直流作為输电网络连接的多区域交直流异步电网将会成为未来一种非常重要和常见的电网结构。

目前，已经有考虑柔性直流输电网络的连续潮流研究，但现有研究重点在于考虑多端柔性直流网络的数学建模和交直流解耦计算过程，并没有考虑VSC-MTDC直流网络控制参数整定方案对系统静态电压稳定裕度的影响[9，10]。直流网络控制参数的整定方案会直接影响负荷增长过程中异步互联系统内的潮流分布，进而对系统的静态电压稳定裕度产生非常大的影响。

针对现有连续潮流研究的缺陷，本文提出了一种基于连续潮流计算的换流站整定参数优化方法。该方法以全网静态电压稳定裕度最大为优化目标，以分区断面传输功率恒定为等式约束条件，以遗传算法为计算核心，对各VSC换流站的整定控制参数进行优化。本文以IEEE-RTS96仿真系统为基础进行算例仿真，仿真验证了本文所提优化方法的有效性。结果显示，本文所提优化方法可以在保证分区间传输功率恒定的前提下得到最优的换流站控制参數整定方案，有效提升系统的电压稳定性。

2 多端柔性直流输电网络的潮流模型

在对多端柔性直流输电网络（VSC-MTDC）进行潮流建模时，采用如下假设：①VSC换流站交流端电压为正弦波形，并只考虑其基频和正序分量;②换流器所产生的谐波分量不被考虑;③所有开关被认为是理想开关。电压源型换流器由换流桥、换流电抗器、交流滤波器、直流电容和直流电缆组成。一般将换流器交流侧与之直接相连的节点称为公共耦合节点，即PCC节点。

为了更方便地描述建模过程，本章作如下的变量符号定义：记第[i]个VSC为[VSCi];对于[VSCi]，其所连PCC节点电压的基波向量为[Vti]，其换流桥输出线电压的基波向量为[Vci]，两者相角差为[δi]，即[δi=θti-θci];[Xli]和[Xci]分别表示换流电抗器和交流滤波器的基波电抗;[Ri]为代表换流桥有功损耗的等效电阻;[Psi]和[Qsi]为从交流网络注入[VSCi]的有功功率和无功功率;[Vdi]表示[VSCi]输出的直流电压;[Idi]为注入多端直流网络的直流电流。

郑超等人[11]的研究给出了VSC-MTDC的潮流模型，具体见式（1）至式（3）。

[Psi-μiMi2VtiVdiYisin（δi-αi）-V2tiYisinαi=0Qsi+μiMi2VtiVdiYicos（δi-αi）-V2tiYicosαi-V2tiXci=0VdiIdi-μiMi2VtiVdiYisin（δi+αi）+μ2iM2i2V2diYisinαi=0] （1）

[Idi-j=1ncgdijVdj=0]                         （2）

[ci（Vdi，Vti，Psi，Qsi）=0]                     （3）

式中，[μi]为直流电压利用率，当调制方式为正弦脉宽调制（Sinusoidal Pulse Width Modulation，SPWN）时，[μi]=[3/2];当调制方式为空间矢量脉宽调制（Space Vector Pulse Width Modulation，SVPWN）时，[μi]=1。[Mi]为电压调制度;[gdij][ 为]直流网络i与j节点之间的直流电缆电导;[nc]为直流网络的节点数，也是换流器个数;[Yi]和[αi]分别为[Xli]和[Ri]所对应的导纳和导纳角。

式（3）为换流器的控制方程。[VSCi]关联的四个状态量为[Vdi、Vti、Psi、Qsi]，需要设定其中两个为控制目标，常见的组合方式有四种：①[Vdi]和[Qsi]恒定控制;②[Vdi]和[Vti]恒定控制;③[Psi]和[Qsi]恒定控制;④[Psi]和[Vti]恒定控制。正常情况下，一端选择直流电压给定的①或者②，以维持直流电压恒定;其他端选择有功给定的③或者④，以控制传输有功为指定值。

3 异步互联电网下连续潮流模型

以VSC-HVDC进行连接的异步互联电网的典型结构，两个区域电网（子网A和子网B）由一组VSC-HVDC直流输电网络进行连接，[VSC1]和[VSC2]分别为两个区域电网所连接的换流站，[SA]和[SB]分别表示两个区域电网内所有交流节点集合。每个分区内交流节点可以被分为四种类型：①PV节点（排除掉PCC节点）;②PQ节点（排除掉PCC节点）;③PVθ节点，亦即为该分区的相角参考点;④PCC节点。

对于A分区交流网络，以[ΩAPQ]、[ΩAPV]、[ΩAPVθ]和[ΩAPCC]分别表示所示A分区内PQ、PV、PVθ和PCC节点集合，则A分区内节点的参数化潮流约束方程[FA]（·）可以表示为式（4）。

[ΔPi=PGi0-PLi0-λPLi0-Vij=1nVj（Gijcosθij+Bijsinθij）=0，i∈ΩAPV，ΩAPVθΔPi=-（1+λ）PLi0-Vij=1nVj（Gijcosθij+Bijsinθij）=0，i∈ΩAPQΔPi=PGi0-（1+λ）PLi0-Vij=1nVj（Gijcosθij+Bijsinθij）-PsiA=0，i∈ΩAPPCΔQi=-（1+λ）QLi0-Vij=1nVj（Gijsinθij-Bijcosθij）=0，i∈ΩAPQΔQi=-（1+λ）QLi0-Vij=1nVj（Gijsinθij-Bijcosθij）-QsiA=0，i∈ΩAPPC]          （4）

式中，[ PLi0]和[QLi0]分别代表节点[i]在扰动前的初始负荷;[PGi0]和[PGi]分别代表节点i处发电机组扰动前后的有功出力;[PsiA]和[QsiA]分别表示当前从A分区系统注入换流站[VSCi]的有功和无功功率;λ为负荷增长因子。类似地，B分区内的节点的潮流约束方程[FB]（·）可以参考进行列写。

当采用弧长法时，步长约束方程[ω]（·）可以表示为：

[ω（xA，xB，λ）=（xA-xprvA）T（xA-xprvA）+（xB-xprvB）T（xB-xprvB）+...+（λ-λprv）2-σ2=0]             （5）

式中，[xA]和[xprvA]分别为当前点和上一个运行点的A分区节点电压相角和幅值;[xB]和[xprvB]分别为当前点和上一个运行点的B分区节点电压相角和幅值;[σ]为控制步长;[λpre]为前一个运行点对应的负荷增长因子。

自此，异步互联电网下的连续潮流模型可以表示为：

[FA（xA，fA，PsiA，QsiA，λ）=0FB（xB，fB，PsiB，QsiB，λ）=0D（Vdi，Idi，δi，Mi，Vti，Psi，Qsi）=0ω（xA，xB，λ）=0]                  （6）

式中，[FA]（·）和[FB]（·）表示A、B交流分區内考虑频率特性的节点参数化潮流约束方程，即方程（4）;D（·）表示直流系统潮流约束方程和控制方程，由式（1）减（3）构成;[ω]（·）表示步长约束方程，即方程（5）。

4 基于连续潮流模型的优化方法

对于以VSC-MTDC网络为联络线的交直流互联异步电网，其联络线断面功率总和需要满足断面功率交易约束。尽管VSC交流端注入的有功功率和无功功率可以独立进行控制，但在短时间内VSC的整定参数无法快速地随负荷增长而调整。所以，在模拟负荷增长的过程中，认为VSC的控制方式和整定值保持不变是一种比较合理的假设。

显然，不同的VSC控制整定值下，互联异步电网的负荷裕度不同，因而寻找能使负荷裕度最大的整定值参数也成为控制目标。在本文提出的连续潮流模型的基础上，考虑断面功率交易约束，得到一个外层优化问题：

[max  λs.t.   i∈bus_t_ABPsi-Ptotal_spec=0  ]             （7）

在式（7）中，目标函数是整个含VSC-MTDC网络的交直流互联异步电网的负荷裕度，可以通过本文提出的异步互联电网连续潮流模型即式（6）计算得到。优化变量是各个VSC的整定值参数，如[Udi，Uti，Psi，Qsi]。式中[，bus_t_AB]为A、B子区域之间传输断面上的交节点集合;[Ptotal_spec]为多端柔直输电网络断面上的总有功功率整定值。

MATLAB的遗传算法（Genetic Algorithm，GA）工具箱可以很好地解决这个问题。对于每一代种群中的每一个个体，都可以通过第V节中的步骤A-F来计算其适应度。

5 算例基础数据与仿真条件

为了证明本文所提出连续潮流模型的有效性，本文采用修改后的两区域IEEE-RTS96（MRTS）测试系统[12]。所有计算都在MATLAB环境下编写。在原有的MRTS测试系统基础上，三条输电线被两个MTDC网络所替代：在138kV系统中，107—203线路被一个三端口150kV的MTDC网络所替代，此多端柔性直流网络连接两个异步电网和一个风电场（节点301和节点302）。在345kV系统中，113—215线路、123—217线路被一个四端口300kV多端柔性直流网络所替代。

VSC的基本参数和整定值见表格1和表格2。VSC2、VSC6、VSC7构成联络线传输断面，通过断面注入右侧分区电网交易功率设定为120MW。三个子区域的功率平衡节点分别为115、201、302。节点107处一台输出功率为80MW的机组（U100）停运，节点201处一台输出功率为76MW的机组（U76）停运，节点302处增设一台出力为150MW的风力发电机。目标状态时负荷和发电机出力为初始状态的1.5倍。

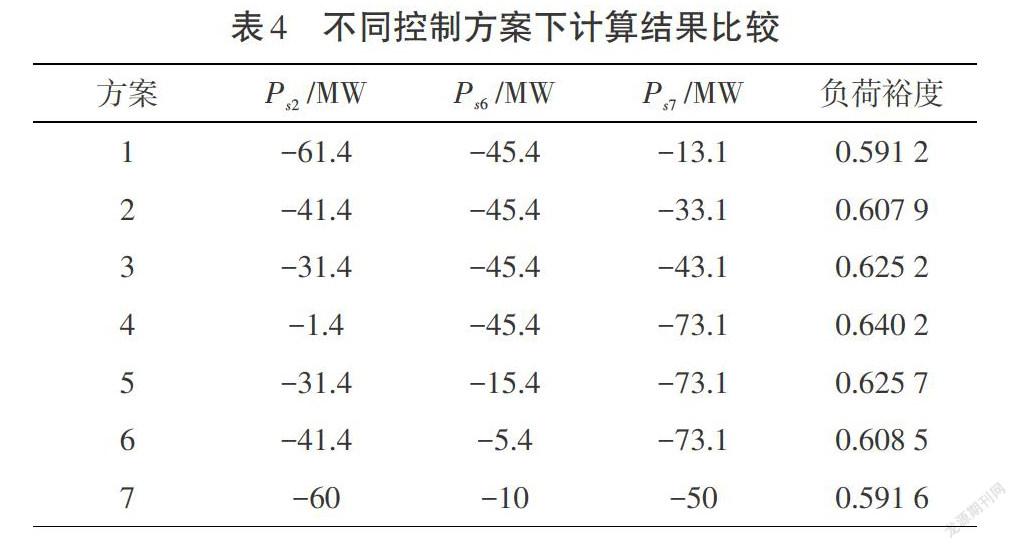
表3为遗传算法的参数设置与优化结果，表4为不同换流站控制参数整定方案下的计算结果对比。表4中，仿真方案4为本文优化方法所得到的最优控制参数整定方案。比较方案1至方案7的仿真结果可以发现，优化后的整定值方案可以使全网负荷裕度最大，算例仿真证明了外层优化方法的有效性。

6 结论

针对由多端口柔性直流输电网络（VSC-MTDC）连接的异步互联电网，本文提出了一种基于连续潮流计算的换流站整定参数优化方法。仿真结果显示，本文所提方法可以在保证分区间传输功率恒定的前提下得到最优的换流站整定控制参数方案，有效提升系统的电压稳定性。

参考文献：

[1]王锡凡，万方良，杜正春.现代电力系统分析[M].北京：科学出版社，2003.

[2]程浩忠，吴浩.电力系统无功与电压稳定性[M].北京：中国电力出版社，2004.

[3]余贻鑫，董存.美加“8.14大停电”过程中的电压崩溃[J].电力设备，2004（3）：4-7.

[4]李春艳，孙元章，陈向宜，等.西欧“11.4”大停电事故的初步分析及防止我国大面积停电事故的措施[J].电网技术，2006（24）：16-21.

[5]易俊，卜广全，郭强，等.巴西“3.21”大停电事故分析及对中国电网的启示[J].电力系统自动化，2018（2）：1-6.

[6] Beerten J， Cole S， Belmans R. Generalized Steady-State VSC MTDC Model for Sequential AC/DC Power Flow Algorithms[J]. IEEE Transactions on Power Systems， 2012（2）：821-829.

[7] Zhang X P. Multiterminal voltage-sourced converter-based HVDC models for power flow analysis[J]. IEEE Transactions on Power Systems，2004（4）：1877-1884.

[8]G. Asplund.Application of HVDC light to power system enhancement[J].IEEE 2000 PES Winter Meeting，2000（7）23-27.

[9]王振浩，由作宇，黄亚磊，等.基于连续潮流法的含双端VSC-HVDC交直流系统负荷裕度分析[J].电力系统保护与控制，2018（6）：9-15.

[10]高亚静，王志，梁海峰.含经VSC-HVDC并网海上风电场的电网可用输电能力计算[J].现代电力，2013（4）：9-23.

[11]郑超，周孝信，李若梅，等.VSC-HVDC稳态特性与潮流算法的研究[J].中国电机工程学报，2005（6）：1-5.

[12] Grigg C， Wong P， Albrecht P， et al. The IEEE Reliability Test System-1996. A report prepared by the Reliability Test System Task Force of the Application of Probability Methods Subcommittee[J]. IEEE Transactions on Power Systems， 2002（3）：1010-1020.