基于三角网格模型的剖切轮廓自动补面方法
李定林 罗茜 孙廷昌 高彦明 闫双键


摘要:本文介绍了一种基于三角网格模型的剖切轮廓自动补面算法,包括:建立三维拓扑数据结构,记录三维模型的几何信息和拓扑信息;在三维模型的投影面上定义切割路径和切割方向,自动生成三维模型的切割面;切割面与构成物体的三角面片进行相交运算,形成离散的线段集;对切割面上的离散线段集进行追踪拟合,得到物体的封闭轮廓线,确定轮廓线的包含关系;对封闭轮廓线的包围区域进行三角剖分,生成实体的剖面图。本文的算法实现了虚拟现实环境下三维模型的实体剖面、自动补面和材质继承,既能够在虚拟现实环境下准确可视化的描述三维模型的实体剖面,又可相对准确的继承材质纹理,且同时具有较好的实时性。
关键词:三角网格模型;网格剖切;轮廓信息
引言
三维模型中的三角网格模型具有许多良好的几何特性,它能够用多个面片逼近复杂形体的表面,而且容易处理,因此三角网格模型被广泛应用于计算机图形学、机械仿真、科学计算可视化等领域[1]。剖面轮廓线是三维模型的一个重要特征,它代表模型在某一位置处的大致轮廓和几何形状[2],并体现三维模型的基本外观。对三维表面模型的剖切是指直接在屏幕上对三维模型进行任意方向剖切,用户可以方便地观察模型截面的大小形状,以实现对模型截面的宏观认识。
现状分析
虚拟现实环境中的三维模型由巨大的三角网格模型重构而成,现有的虚拟现实三维模型剖切[3–5]主要利用三角网格与剖切平面的空间位置关系得到模型剖切后三角网格的空间信息,现有的剖切技术主要采用空间中的面面求交运算[6],即三角网格的三边都与剖切面进行计算。
通过对现有的技术进行研究分析,存在以下方面的问题:
现有方法造成的计算量相当庞大,严重影响剖切的实时性。
目前的剖切方法中,三角网格与剖切面相交并的剖切面并不考虑实体的闭合面,无闭合面即空心剖切,更不会有实体剖面补面。剖切后的网格模型剖切面不能自动补面,用户不能很直观的从剖面上分析出来哪些是实体模型,哪些是面或壳模型,给实际培训过程会带来一些困难。
文献[2]中公开了一种基于三角网格模型的剖面轮廓信息提取[2],其采用OBJ格式的三维模型数据,利用分层切面和邻接排序算法,获得三角网格模型的剖面轮廓信息。该方法对有拓扑错误的模型有较好的适用性,但是该方法在获得封闭的剖面轮廓环的过程中,未考虑补面时材质纹理的继承问题。
因此该问题成为了水电站三维精确模型基于虚拟现实技术的培训系统中的一个亟待解决的重点和难点。
剖切轮廓自动补面算法
本文所采用的切割算法的原理为:将物体的三维模型投影在二维平面上并获取物体的投影图,在二维平面上选择定义切割路径和切割方向,然后自动生成一个三维物体的切割面;用切割面和三维物体进行一系列的相交运算,对三维物体进行切割,得到一组离散的线段,再对离散的线段进行追踪拟合,形成封闭的轮廓线,从而构成一个剖面图。其形成的封闭轮廓线结构就是三维物体在该切割面上的内部结构,从而可以观察得到准确的三维物体的内部构成。
针对现有技术存在的问题,本文提供一种应用于虚拟现实环境下三维模型的实体剖切,首先对于虚拟现实环境下物体的三维模型,建立三维拓扑数据结构;然后在三维模型的投影面[7]上定义切割路径和切割方向,自动生成三维模型的切割面;对切割面上的离散线段集进行追踪拟合,得到物体的封闭轮廓线;最后对封闭轮廓线的包围区域进行三角剖分,生成实体的剖面图。
算法流程图和拓扑关系图如图1和图2所示。
建立三维拓扑数据结构
对于虚拟现实环境下物体的三维模型,建立三维拓扑数据结构,所述三维拓扑数据结构记录三维模型的几何信息和拓扑信息,包括构建三维模型的顶点、边、面、体的数量及纹理信息;其中,顶点的信息包括顶点编号、坐标、颜色;面的信息包括构成面的顶点数量、顶点编号、面的颜色、顶点序列;体的信息包括体的面数、面编号、纹理标号、层次标号。
这样设置的优点是:
通过建立三维拓扑数据结构,能够高效查询和检索网格几何信息,并对网格空间拓扑信息数据结构进行修改和重构。
有利于在虚拟现实环境下进行三维模型的实体剖切,并能在剖切过程中进行自动补面以及继承原模型的材质纹理。
网格信息不仅存储了网格的空间信息,同时还存储了其几何元素(如顶点、边、三角形等)之间的连接关系的拓扑信息。在三维模型的转化过程中,按照统一标准属性和格式对每一个三维模型的几何信息、拓扑信息进行记录,获取构建三维模型的顶点、边、面、体的数量以及纹理信息,建立三维拓扑数据结构对这些空间拓扑信息进行查询、修改和重构。通过这种信息处理的方式,在剖切的过程中利用切割平面对物体三维模型相交的点运算形成离散的交线,利用交线数组得到物体的封闭轮廓线。同时对交线与重构的网格拓扑信息的关系进行追踪和检索、检测、计算,对得到的重构拓扑信息进行格式运算,可形成新的物体三维模型。
生成三维模型的切割面
在三维模型的投影面上定义切割路径和切割方向,自动生成三维模型的切割面。生成三维模型的切割面的步骤具体包括:
在给定视点下,对物体的三维模型进行隐藏线、隐藏面的消除处理,得到物體的二维效果图;
在物体的二维投影平面上,定义切割路径和切割方向;
将切割路径和切割方向反投影到三维空间中,形成三维模型的切割面。
这样设置的好处是:相对于现有技术中的剖面深度缓存(Z缓存)算法或八叉树数据结构算法来说,这里采用的基于网格的切割算法的处理效率要更好,且在此基础上采用基于网格的拓扑信息进行离散线段的追踪亦保证了剖面轮廓自动补面的准确性。
形成离散的线段集
切割面与构成物体的三角面片进行相交运算,形成离散的线段集。包括:首先确定切割面方程;然后利用二叉树结构遍历叶节点中的三角网格,判断网格是否与切割面相交,如果相交,则求出切割面与网格的交点,得到离散的线段,对离散线段的拓扑信息进行处理,将处理后信息存入上下链表;如果判断得出网格与切割面不想交,则判断网格与切割面位置,并将原信息存入上下链表。
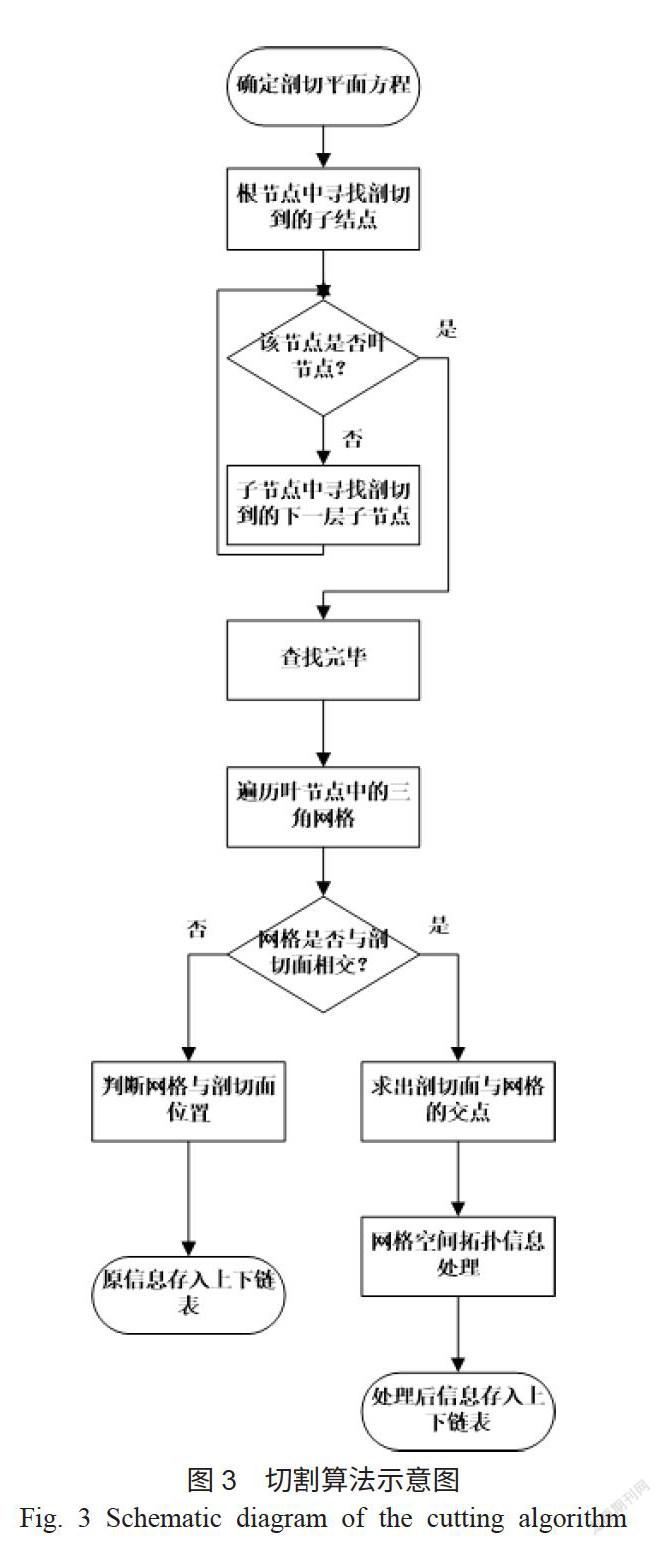
切割算法流程如图3所示。剖切轮廓自动补面算法中切割算法包括:
确定切割面方程;
一个平面通过的空间三个点,,,平面方程为:
在根节点中寻找剖切到的子节点;
判断该节点是否叶节点,如果是,则该节点查找完毕,继续下一步骤;如果否,则子节点中寻找剖切到的下一层子节点,再判断该下一层子节点是否叶节点;
遍历叶节点中的三角网格,判断网格是否与剖切面相交,如果是,则求出剖切面与网格的交点,对网格空间拓扑信息进行处理,将处理后信息存入上下链表;如果否,则判断网格与剖切面位置,将原信息存入上下链表。
确定轮廓线的包含关系
对切割面上的离散线段集进行追踪拟合,得到物体的封闭轮廓线,确定轮廓线的包含关系。包括:对离散线段的拓扑信息进行查询、修改和重构,对离散线段与重构后的拓扑信息的关系进行格式运算,形成新的三维物体;
这样设置的好处是:通过三维拓扑数据结构中记录的离散线段与原三维模型关联的拓扑信息,能够在离散线段的追踪拟合过程中准确的计算出原三维模型的闭合轮廓,从而准确的进行实体剖切。同时,在进行离散线段的拟合过程中,依据记录的离散线段的材质纹理信息的标号,对拟合的离散线段进行材质纹理信息的修改和拓扑关系的重构,使得得到的实体剖切图能够准确的继承原模型的材质纹理。
对封闭轮廓线的包围区域进行三角剖分,生成实体的剖面图。
效果与现有技术相比,本算法的有益效果是:
实现了虚拟现实环境下三维模型的实体剖面、自动补面和材质继承,既能够在虚拟现实环境下准确可视化的描述三维模型的实体剖面,又可相对准确的继承材质纹理,且同时具有较好的实时性;
采用基于网格的切割算法进行切割面与三角面片的相交运算,并基于网格的拓扑信息进行离散线段的追踪,保证了虚拟现实环境下三维模型剖切的效率和准确率;
通过建立三维拓扑数据结构,能够高效查询和检索网格几何信息,并对网格空间拓扑信息数据结构进行修改和重构,保证虚拟现实环境下三维模型实体剖切中材质纹理继承的准确性。
结论
本算法的目的是针对现有技术存在的问题,提供一种基于三角网格模型的剖切轮廓自动补面算法。该算法实现了虚拟现实环境下三维模型的实体剖面、自动补面和材质继承,既能够在虚拟现实环境下准确可视化的描述三维模型的实体剖面,又可相对准确的继承材质纹理,且同时具有较好的实时性。
参考文献
王静亚,方亮,郝敬宾. STL模型特征面片自适应分层算法[J].计算机应用研究,2011(6):367–370+374.
张小青,吴坤华,黄鹤.基于三角网格模型的剖面轮廓信息提取[J].测绘通报,2012(9)26–28.
潘海鹏,周天瑞,朱根松. STL模型切片轮廓数据的生成算法研究[J].中国机械工程,2007(17):64–67.
王泉德.任意三角网格模型體积的快速精确计算方法[J].计算机工程与应用,2009(18):36–38+62.
谢存禧,李仲阳,成晓阳. STL文件毗邻关系的建立与切片算法研究[J].华南理工大学学报(自然科学版),2000(3):34–39.
张小青,朱光,侯妙乐.基于四面体的不规则表面文物体积计算[J].测绘通报,2011(10):54–56.
袁青.基于投影面的三维物体剖面图的自动生成算法[D].西安科技大学,2013.

