基于卡门涡街效应的压电悬臂梁的发电仿真分析

李海宁 王海峰 郭修宇 孙凯利 崔宜梁

摘要： 为研究压电体在海洋中受迫振动发生形变产生电场的复杂问题，本文以柔性压电片（聚偏氟乙烯作为压电体）为例，基于ANSYS有限元仿真软件，建立流体固体压电三场耦合的仿真模型，研究基于卡门涡街效应的柔性压电悬臂梁的发电能力与水速、圆柱直径、压电片尺寸之间的关系。分析结果表明，在压电片尺寸和水流速度相同的情况下，圆柱直径为40 mm时，产生的电压最大为195 V;在压电片尺寸和圆柱直径相同的情况下，水流速度为02 m/s时，产生的电压最大为195 V;在水流速度和圆柱直径相同的情况下，当压电片长度为170 mm时，产生的电压最大为185 V。该研究为以后相关研究提供了理论基础。

关键词： 卡门涡街; 压电悬臂梁; 柔性压电发电装置; ANSYS; 多物理场耦合; 数值水槽

中图分类号： TM619; TN384  文献标识码： A

1 压电悬臂梁系统的计算模型及理论

液态流场计算区域为长1 500 mm，宽500 mm，高200 mm的立方体空间，流场左端为进口边界，右端为出口边界，定义出口为压力流出边界，定义顶面和前后两个面为对称边界，定义底面为壁面边界。当水流从左侧进口流入流场时，由于钝体的阻挡，会产生卡门涡街效应，涡街脱落，从而改变压电片两侧的压力差。液体流场模型的数值尺寸如图1所示，系统耦合仿真流程图如图2所示。

2 模型的网格划分

利用网格划分软件集成计算机工程与制造代码（the integrated computer engineering and manufacturing code，ICEM）對流场进行网格划分，将整个流场区域划分为13个子区域，网格划分的难点在于压电片部分，其它区域的划分与单圆柱绕流的网格划分方法相同。为减小计算误差，在圆柱钝体近壁面处采用加密的处理方式，加密后，第1层网格到壁面的距离为03 mm，按照12倍尺寸增长过渡。为了使网格过渡的更加平稳，将圆柱体上下左右4个方向中的接触面进行相关设置。流场网格划分如图3所示，柔性压电片网格划分图如4所示。网格的总数为85×105个。

3 仿真的结果与分析

仿真分析时，水流速度分别为005，01，015，02 m/s，圆柱直径分别为20，30，40，50，60 mm，压电片宽度为10 mm，长度分别为40，70，170 mm。综合水速、圆柱直径、压电片尺寸3个因素，本文研究基于卡门涡街效应的柔性压电发电系统的发电能力。

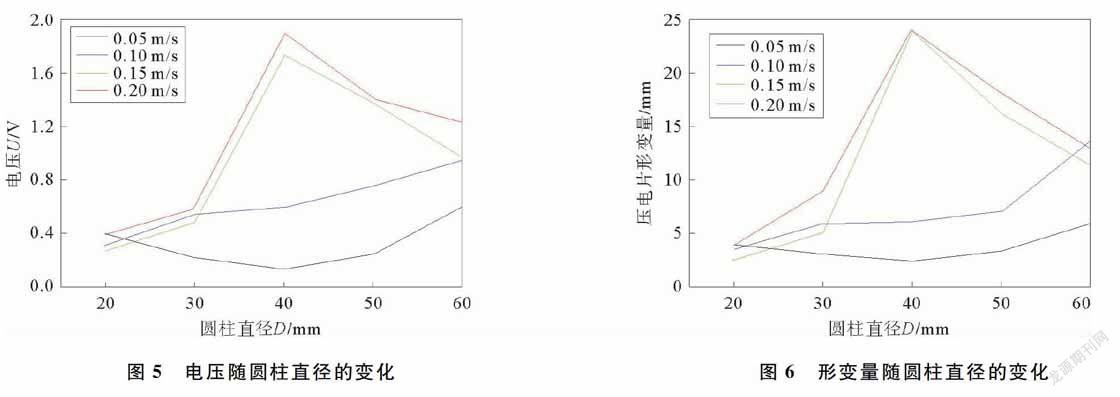
1） 压电片尺寸相同、水流速度相同，圆柱直径不同。在不同水流速度下，电压随圆柱直径的变化如图5所示，形变量随圆柱直径的变化如图6所示。

由图5可以看出，当水流速度较小时，电压较低，平均为05 V左右;当水流速度较大时，电压变化较大，且在圆柱直径为40 mm时，电压达到最大值1.95 V。此后，电压随圆柱直径的增大而减小，这是由于当圆柱体直径达到40 mm时，相应的卡门涡街效应也达到最大，此时脱落频率最高，因此压电片的摆动幅度最大，产生的电压也最大，随着圆柱直径继续增大，卡门涡街效应减弱，电压也逐渐降低。由图5和图6对比可以看出，形变量与电压的变化曲线基本一致，在圆柱直径为40 mm时达到最大形变量为27 mm，然后逐渐变小。

2） 压电片尺寸大小相同、圆柱直径相同，水流速度不同。在不同圆柱直径下，电压随水流速度的变化如图7所示，形变量随水流速度的变化如图8所示。

由图7可以看出，当圆柱直径较小时，电压并没有随着水流速度的增加而产生明显变化，维持在04 V左右;当圆柱直径较大时，电压随水流速度增加而增加，当圆柱直径为40 mm时，电压最大，其值为1.95 V。由图7与图8对比可以看出，形变量与电压的变化曲线基本一致，形变量和电压生成量的大小关系密切。当圆柱直径为40 mm时，形变量最大，其值为23 mm。

3） 水流速度相同、圆柱直径相同，压电片尺寸大小不同。不同水流速度下，电压随柔性压电片尺寸的变化如图9所示，形变量随柔性压电片尺寸的变化如图10所示。

由图9可以看出，当水流速度为005 m/s时，电压较小，维持在01 V左右，这是由于当水流速度较低时，生成的卡门涡街效应较弱，使压电片的摆动幅度较小;当水流速度为01 m/s时，70 mm的压电片恰好处于旋涡脱落之中，电压相对较大，约为08 V，当压电片增加至170 mm时，电压降低，这是由于压电片处于多个旋涡中，反方向的摆动会产生相反的电压，抵消掉部分电压;当水流速度较大时，压电片的长度越长，产生的电压越大，最大电压值约为185 V。由图10可以看出，形变量的变与电压的变化曲线基本一致，当压电片长为170 mm，水流速度为02 m/s时，形变量最大，其值为225 mm。

4 结束语

本文以柔性压电片（聚偏氟乙烯作为压电体）为例，基于ANSYS有限元仿真软件，建立流体固体

压电三场耦合的仿真模型。通过对水速、圆柱直径及压电片尺寸的控制，得到三者与压电片之间电压值的关系。仿真结果可知，在压电片尺寸和水速相同的情况下，圆柱直径为40 mm时，产生的电压最大值为1.95 V;在压电片尺寸和圆柱直径相同的情况下，水速为02 m/s时，产生的电压最大值为1.95 V;在水速和圆柱直径相同的情况下，压电片的长度为170 mm时，产生的电压最大值为1.85 V。该研究为以后相关研究提供了理论基础。

参考文献：

[1] 赵兴强， 王军雷， 蔡骏， 等. 基于风致振动效应的微型风能收集器研究现状[J]. 振动与冲击， 2017， 36（16）： 106112.

[2] Taylor G W， Burns J R， Kammann S A， et al. The energy harvesting eel： a small subsurface ocean/river power generator[J]. IEEE Journal of Oceanic Engineering， 2001， 26（4）：539547.

[3] Pobering S， Schwesinger N. A Novel Hydropower Harvesting Device[C]∥2004 International Conference on MEMS， NANO and Smart Systems. Banff， AB， Canada： IEEE， 2004：16.

[4] Mehmood A， Abdelkefi A， Hajj M R， et al. Piezoelectric energy harvesting from vortexinduced vibrations of circular cylinder[J]. Journal of Sound & Vibration， 2013， 332（19）： 46564667.

[5] Akaydin H D， Elvin N， Andreopoulos Y. The performance of a selfexcited fluidic energy harvester[J]. Smart Materials & Structures， 2012， 21（2）： 025007.

[6] Weinstein L A， Cacan M R， So P M， et al. Vortex shedding induced energy harvesting from piezoelectric materialsin heating， ventilation and air conditioning flows[J]. Smart Materials & Structures， 2012， 21（4）： 4500345012.

[7] MolinoMineroRe E， Carbonell M， FisacFuentes C. Piezoelectric energy harvesting from induced vortex in water flow[C]∥Instrumentation and Measurement Technology Conference. Graz Austrilia： IEEE， 2012.

[8] 朱庆飞. 涡流场中仿生摆动翼的水动力性能研究[D]. 哈尔滨： 哈尔滨工程大学， 2013.

[9] 贾来兵. 二维流场中板状柔性体与流体相互作用的研究[D]. 合肥： 中国科学技术大学， 2009.

[10] 王晓聪， 桂洪斌， 刘洋. 三维有限长圆柱绕流数值模拟[J]. 中国舰船研究， 2018， 13（2）： 2734.

[11] 王凯鹏， 赵西增. 横向受迫振荡圆柱绕流升阻力系数研究[J]. 江苏科技大学学报： 自然科学版， 2017， 31（5）： 579585.

[12] Prasanth T K， Mittal S. Flowinduced oscillation of two circular cylinders in tandem arrangement at low Re [J]. Journal of fluids and structures， 2009， 25（6）： 1 0291 048.

[13] AIMallal Q M， Lawrence K P， Kocabiyik S. Forced streamwise oscillations of a circular cylinder ： Lockedon modes and resulting fluid forces[J]. Journal of Fluids and Structures， 2007， 23（5）： 681701.

[14] 樊娟娟， 唐友刚， 张若瑜， 等. 高雷诺数下圆柱绕流与大振幅比受迫振动的数值模拟[J]. 水动力学研究与进展： A辑， 2012， 27（1）： 2432.

[15] 滕丽娟， 张志伟， 武燕蕾. 湍流模型下双柱绕流升阻力系数数值模拟[J]. 河北工程大学学报： 自然科学版， 2009， 26（2）： 5154.

[16] 滕丽娟. 不同排列方式下的双圆柱、三圆柱绕流数值模拟[D]. 邯郸： 河北工程大学， 2009.

[17] Kuo C H， Chen C C. Passive control of wake flow by two small control cylinders at Reynolds number 80[J]. Journalof Fluids and Structures， 2009， 25（6）： 10211028.

[18] 張智娟， 倪超， 侯立群. 悬臂梁双晶压电片不同连接方式发电性能[J]. 电子器件， 2018. 41（4）： 893897.

[19] 顾睿洋， 姜添曦， 何清波. 一种弹性折叠压电悬臂梁的结构设计及发电特性研究[J]. 机械与电子， 2018. 36（7）： 1518.

[20] 胡世军， 杨志云， 李小强. 基于ANSYS的悬臂梁压电陶瓷单晶片发电特性仿真分析[J]. 机械制造， 2017. 55（1）： 5558， 62.