具有带外陡降特性的双通带频率选择表面设计

唐旭英 唐金元 王翠珍

摘要： 针对多通带频率选择表面带外选择性能差的问题，设计了一种具有带外陡降特性的双通带频率选择表面（dualpassband frequency selective surface，DPFSS）。该设计由两层相同的栅格方环单元和一层方环贴片单元组成，可以通过调整单元几何参数，实现对传输零点频率的独立控制。同时，按照物理结构建立等效电路模型，并采用CST对本文提出的FSS进行仿真分析。仿真结果表明，该设计可以在C、X频段内形成两个传输通带，位于通带两侧的零点形成了陡峭的上升沿和下降沿，缩短了过渡带，同时高频零点形成了宽传输阻带，进一步提升了带外选择性能，在垂直入射的情况下，可以实现5.48～6.54 GHz和8.73～10.04 GHz的通带范围（-1 dB）及10.32～17.55 GHz的阻带范围（-10 dB），具有良好的极化稳定性和角度稳定性。该研究具有一定的实际应用价值。

关键词： 频率选择表面（FSS）; 双通带; 带外陡降; 等效电路模型

中图分类号： TN62; TN925+.93  文献标识码： A

频率选择表面（frequency selective surface，FSS）对不同极化方式和入射角度的电磁波具有频率选择特性。FSS独特的空间滤波特性，使其在极化转换器、双工器、反射面天线的副反射器、雷达天线罩、电磁吸波材料等方面有广泛应用，成为微波和天线研究领域的一个重要方向[13]。FSS的分析方法有很多种，其中等效电路法（equivalent circuit method，ECM）具有简明直观、分析速度快、能够解释结构物理特性的优点，在FSS分析中广泛应用。其原理是按照导体层的几何结构，将之等效为由集总元件组成的电路模型，集总元件参数受导体层几何尺寸、层间耦合反应和介质层参数控制。等效电路模型准确建立后，可以快速分析FSS的传输特性，非常适用于多频段FSS的设计和分析。近年来，随着通信技术的发展，单一频段的通信系统已无法满足高信道容量的需求，在多频段通信系统中，双频带和多频带FSS逐渐成为研究热点。在多频带FSS设计中，分形结构、复合单元、互补结构等形式均可实现多频带的传输特性。李尔平等人[4]利用耶路撒冷十字单元，设计一种具有高频陡降特性的四层FSS，能够在通带高频处形成阻带，以提升高频陡降性;N.Behdad等人[57]利用电抗结构和组合谐振结构，提出了兼具宽通带和高选择性的FSS，并研究了此类高阶FSS的多频化技术;钟涛等人[8]提出了具有良好的角度和极化稳定性的双阻带小型FSS。由于上述结构难以在较为靠近的两个频段内实现带通选频特性，并难以同时兼具良好的带外陡降性，大多数都在高频处存在倍频现象，使带外选择特性恶化，在工程应用中造成诸多不便。基于此，本文设计了一种三层双通带FSS，在垂直入射的情况下，可以实现5.48～6.54 GHz和8.73～10.04 GHz的通带范围（-1dB）及10.32～17.55 GHz的阻带范围（-10dB），具有良好的带外陡降特性、极化稳定性和角度稳定性。该研究具有一定的实际应用价值。

1  FSS设计

1.1  FSS结构与模型建立

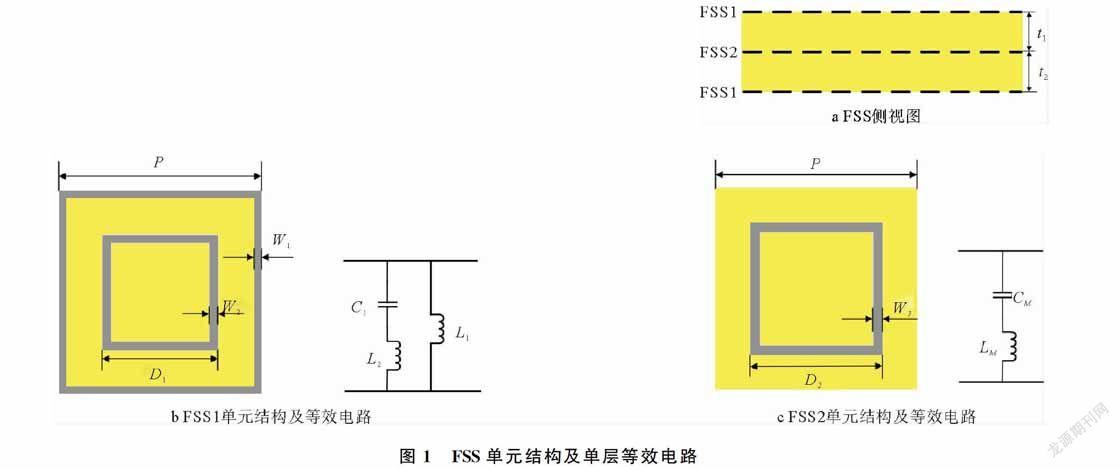
本文对FSS单元结构进行设计，并建立单层等效电路模型，FSS单元结构及单层等效电路模型如图1所示。该FSS由3个导体层及将其两两分隔开的2个介质层（介质层的厚度分别为t1和t2）构成。其中，上、下两层导体层具有相同的结构形式和尺寸，均为栅格方环单元，其结构与等效电路如图1a所示;网栅半宽度为w1，方环外边长为D1，方环宽度为w2，中间层由方环形贴片单元组成，其结构与等效电路如图1b所示;方环外边长为D2，方环宽度为w3，其结构与等效电路如图1c所示，3个导体层具有相同的分布周期P。由于方形结构具有对称性，在垂直入射条件下，电场平行于任意周期延拓方向时，结构具有相同性质，因此具有良好的极化稳定性。对于栅格方环单元，位于单元外侧的导体网栅自身形成的电感可以等效为一个并联电感L1，导体网栅与位于单元内

侧的导体方环之间形成的电容等效为电容C1，导体方环自身形成的电感可以等效为与C1相串联的电感L2 [9]。对于方环贴片单元，相邻导体方环之间形成的电容可等效为CM，导体方环自身形成的电感可等效为LM，两者组成串联电路。

1.2  电路模型拟合结果

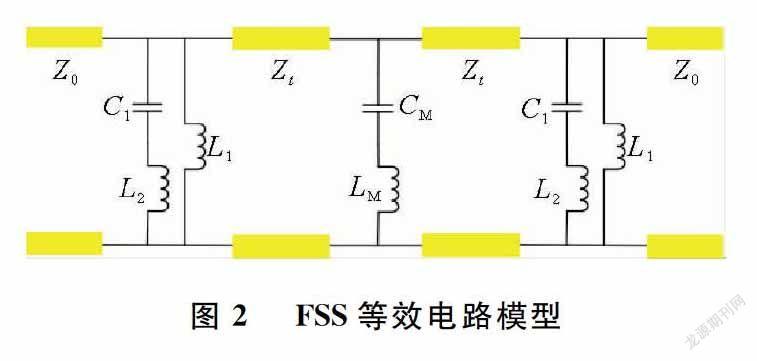
根据1.1中的分析，本文对FSS等效电路模型进行设计，FSS等效电路模型如图2所示。图2中，位于FSS两侧的自由空间，可等效为特性阻抗Z0=377 Ω的半无限长传输线;2个介质层，可等效为两截长度L=t，特性阻抗Zt=Z0/εr的传输线。

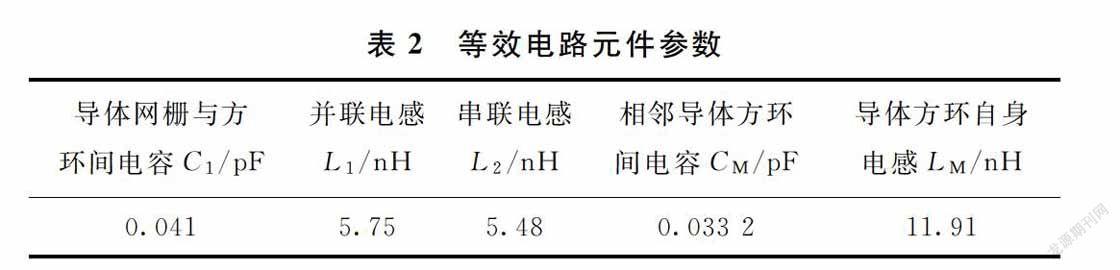
该FSS中，由于3个导体层之间的间隔非常小，层与层之间产生了较为强烈的互耦效应，不同层的元件间相互影响，无法通过经验公式计算元件值。按照图2中所示的电路模型，对元件参数值进行优化拟合，得到满足频对ADS等效电路进行仿真和CTS全波仿真，CST与ADS仿真结果对比如图3所示。由图3可以看出，傳输极点、传输零点的位置和通带范围基本一致，在146 GHz处，CST的全波仿真结果存在一个在ADS仿真中没有得到的传输零点，与106 GHz处的传输零点形成了一个传输阻带，有效缩短了过渡带，提高了带外陡降性。由此可判断出该传输零点为层间耦合产生。等效电路仿真结果与全波仿真结果基本一致，说明本文中所建立的等效电路模型具有参考意义。2  仿真结果及分析

2.1  传输系数分析

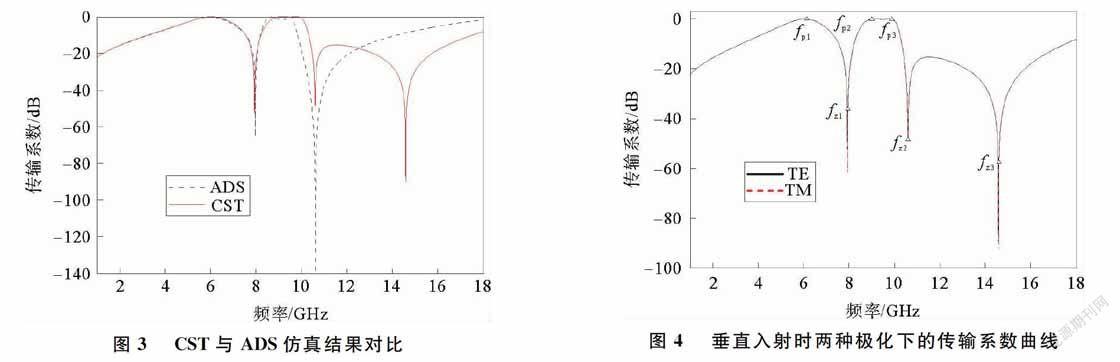
使用CST对本文提出的FSS进行仿真，当电磁波垂直入射时，入射波分别为TE极化和TM极化，垂直入射时两种极化下的传输系数曲线如图4所示。

由图4可以看出，在TE和TM两种极化方式下，传输曲线具有良好的一致性，基本没有产生频率偏移，说明该结构具有良好的极化稳定性，入射波的极化方式对传输特性影响小，可以在工程中得到较好的应用;由图4还可以看出，该FSS结构在601 GHz和95 GHz处均形成了传输通带，低频通带（-1 dB）宽度为1.06 GHz（5.48～6.54 GHz），高频通带宽度为1.31 GHz（8.73～10.04 GHz）。其中，高频通带具有过渡带窄的特性，低频和高频过渡带（传输系数从-1 dB减小到-10 dB的频带）宽度分别为0.52 GHz和0.30 GHz，同时，在高频通带的高频处，传输零点fz2（fz2=10.60 GHz）和fz3（fz3=14.60 GHz）形成了宽度为723 GHz的陡降阻带范围（-10 dB），进一步提高了带外选择性能，并避免了在高频处产生倍频传输极点的可能。

2.2  双频特性分析

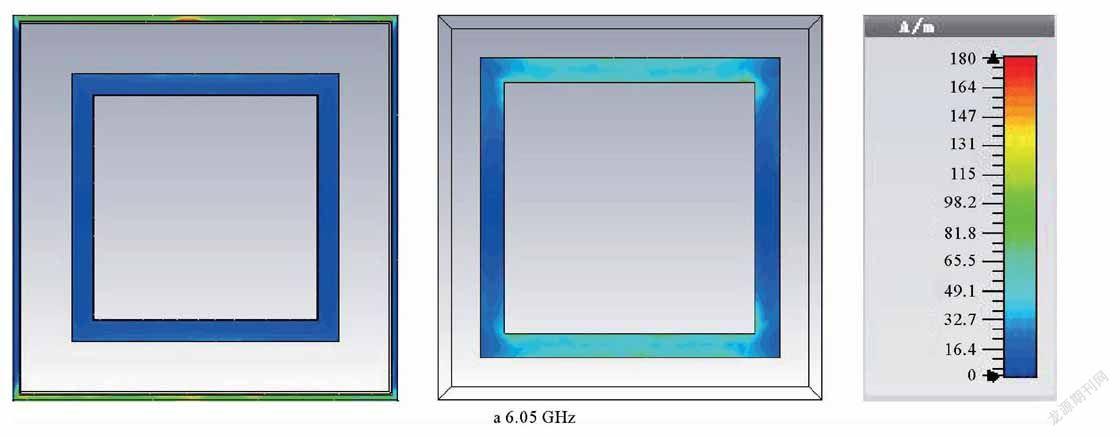
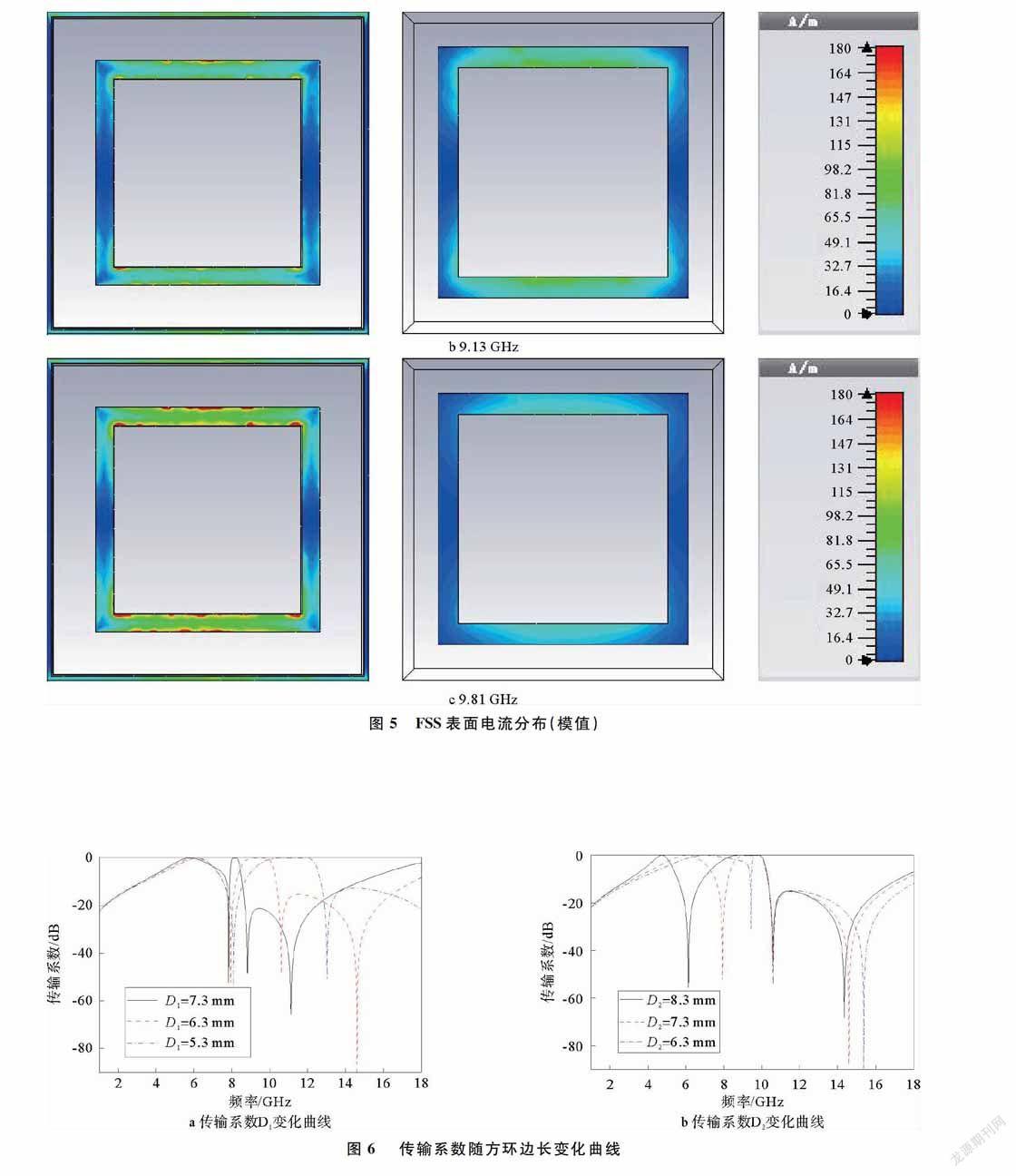
为观察FSS的结构与谐振频率之间的关系，在3个通带极点fp1（fp1=6.05 GHz）、fp2（fp2=9.13 GHz）和fp3（fp3=9.81 GHz）处，对FSS进行表面电流仿真，FSS表面电流分布（模值）如图5所示。

由图5a可以看出，在低频通带极点处，表面电流主要分布在栅格方环层的导体网栅部分和中间层的导体方环上，低频通带主要由网栅部分形成的电感L1和中间层的方环自身电感LM、电容CM形成;由图5b和图5c可以看出，在2个高频通带极点处，表面电流在栅格方环层和中间层上都有分布，但在高频处，栅格方环层的方环上的电流更强，中间层方环上的电流更弱，说明高频通带的第2极点主要受栅格方环层控制，低频极点则由2层栅格方环层和1层中间层共同控制。

分别改变D1和D2的大小，得到传输系数随方环边长变化曲线如图6所示。由图6可以看出，D1主要控制第2零点和高频通带的2个极点;D2主要控制第1零点和高频通带的第1极点，验证了由表面电流分布得到的推测。

3  结束语

本文设计了一种具有带外陡降特性的新型双频带频率选择表面，该设计由2层相同的栅格方环单元和1层方环贴片单元组成，可以通过调整单元几何参数，实现对传输零点频率的独立控制。仿真结果表明，该设计在C、X频段内形成2个传输通带，其中C频段的通带宽度（-1 dB）为106 GHz（548～654 GHz），X频段的通带宽度为131 GHz（873～1004 GHz）;该设计第2通带（X频段通带）具有过渡带窄特性，同时其高频处有宽度为723 GHz（1032～1755 GHz）的陡降阻带范围（-10 dB），进一步提高了带外选择性能，并避免了在高频处产生倍频传输极点的可能，因而具有良好的带外陡降特性。该结构在工作频段内具有良好的极化稳定性和角度稳定性，入射波的极化方式对传输特性影响较小，可以在工程中得到较好的应用。该研究对以后双频带FSS的设计具有较好的理论指导意义。

参考文献：

[1] 高正平， 饶力. 电路模拟技术在吸波结构中的应用[J]. 电子科技大学学报， 1998， 27（2）： 136139.

[2] Munk B A. Frequency selective surfaces： theory and design[M]. USA： WileyInter Science， 2000.

[3] Vardaxoglou J C. Frequency selective surfaces： analysis and design[M]. USA： Wiley Research Studies Press， 1997.

[4] Li T W， Li D， Li E P. A novel FSS structure with high selectivity and excellent angular stability for 5 G communication radome[C]∥2017 10th Global Symposium on MillimeterWaves. Hongkong. China： IEEE， 2017： 5052.

[5] Behdad N， AlJoumayly M， Salehi M. A lowprofile thirdorder bandpass frequency selective surface[J]. IEEE Transactions on Antennas & Propagation， 2009， 57（2）： 460466.

[6] Gao M， Behdad N. A hybrid miniaturizedelement frequency selective surface with a thirdorder bandpass Response[J]. IEEE Antennas & Propagation Letters， 2016， 16： 708711.

[7] Li M， Behdad N. Design of low profile single/dual band highorder frequency selective surfaces[C]∥Antennas and Propagation Society International Symposium （APSURSI）. Toronto， Canada： IEEE， 2010： 14.

[8] 鐘涛， 张厚， 吴瑞， 等. 小型化双频带阻频率选择表面的设计[J]. 空军工程大学学报： 自然科学版， 2016， 17（4）： 8184.

[9] Lee C K， Langley R J. Equivalentcircuit models for frequencyselective surfaces at oblique angles of incidence[J]. IEE Microwaves， Antennas and Propagation， 2008， 132（6）： 395399.

[10] Azemi S， Ghorbani K， Rowe W. 3D frequency selective surfaces with wideband response[C]∥International Workshop on Antenna Technology： Small Antennas， Novel Em Structures and Materials， and Applications. Sydney， Australia： IEEE， 2014： 212215.

[11] Yahya R， Nakamura A， Itami M. 3D UWB bandpass frequency selective surface[C]∥IEEE International Symposium on Antennas and Propagation. Fajardo， Puerto Rico： IEEE， 2016： 959960.

[12] Pelletti， Bianconi， Mittra， et al. Frequency selective surface with wideband quasielliptic bandpass response[J]. Electronics Letters， 2013， 49（17）： 10521053.

[13] Wang D， Che W， Chang Y， et al. A lowprofile frequency selective surface with controllable Triband characteristics[J]. IEEE Antennas and Wireless Propagation Letters， 2013， 12： 468471.

[14] Gao M， Abadi S M， Behdad N. A dualband， inductively coupled miniaturizedelement frequency selective surface with higher order bandpass response[J]. IEEE Transactions on Antennas and Propagation， 2016， 64（8）： 37293734.

[15] 王巖松， 高劲松， 徐念喜， 等. 具有陡降特性的新型混合单元频率选择表面[J]. 物理学报， 2014， 63（7）： 07840210784027.

[16] 王秀芝， 高劲松， 徐念喜. 一种Ku波段/毫米波波段独立双通带微型化频率选择表面[J]. 红外与毫米波学报， 2014， 33（3）： 241247.

[17] 姜聿焘， 张厚， 徐海洋， 等. 一种改进型的Y环双频带通FSS[J]. 微波学报， 2012， 28（6）： 7275.

[18] 鲁戈舞， 张剑， 杨洁颖， 等. 频率选择表面天线罩研究现状与发展趋势[J]. 物理学报， 2013， 62（19）： 110.

[19] 左钰. 新型三维频率选择结构的研究[D]. 南京： 南京大学， 2013.

[20] 侯新宇， 崔尧， 张玉英， 等. 应用等效电路模型的频率选择表面有效分析[J]. 西北工业大学学报， 2006， 24（6）： 686689.