管束式换热器导流结构数值模拟研究与优化设计

张承虎 魏继宏 范丽佳

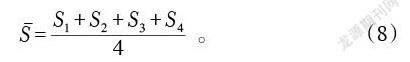
摘要 采用计算流体力学方法，建立进口带导流结构的叉排管束式换热器的CFD模型，分别模拟了换热器入口流速为15、30、46 m/s时，导流结构及叉排管束间的流场分布。以前4排管束间截面的速度标准差为流场均匀性判断依据，研究换热器入口变径长度以及内导流结构进出口尺寸对换热器内部流场均匀性的影响.结果表明：在模拟范围内，随着换热器入口流速减小，热器入口变径长度系数λ最优值减小，导流入口结构比值H1/Wi最优值增加，导流出口结构比值H2/H0最优值减小。

关 键 词 换热器;叉排管束;导流结构;数值模拟;流场优化

中图分类号 TQ053.2     文献标志码 A

Abstract A CFD model of tube-type heat exchanger with diversion structure is constructed by using computational fluid dynamics method. The flow field distributions between the diversion structure and staggered tube bundles have been simulated when the heat exchanger inlet flow rate are 15， 30 and 46 m/s. The velocity standard deviation among the first four rows of tube bundles is the criteria for the flow field uniformity. The effects of the heat exchanger inlet length and the inlet and outlet size of the inner diversion structure on the flow field uniformity in the heat exchanger are studied. The results in the simulation condition show that when the inlet flow velocity decreases， the optimal length factor of inlet reducer decreases， the optimal ratio of the diversion structure inlet size to the heat exchanger inlet size increases and the optimal ratio of the diversion structure outlet size to the heat exchanger body size decreases .

Key words heat exchanger; staggered tube bundles; diversion structure; numerical simulation; flow field optimization

0 前言

在锅炉余热回收系统中，空气横掠管束有着广泛的应用。另外，锅炉中的省煤器、空气预热器等中也存在大量管束[1]。换热器导流结构具有均匀分布流体、减轻流体对换热管冲蚀、强化传热的作用[2] 。合理布置导流结构可使换热器内部流场均匀性提高，增强换热效果。黄德斌等[3]采用3种计算模型：标准k-ε模型、RNG模型和可实现k-ε模型对气流横向冲刷管束换热进行数值模拟，得到不同雷诺数下所适用的计算模型。潘维等[4]通过 CFD技术，模拟了空气横掠管束的流场，结果表明，对于顺排管束，经过5排管子，流速就较为均匀;对于叉排管束，只要经过4排管子，流速就较为均匀。戴伟等[5]对空气横掠叉排管束进行了二维数值模拟，得到了管束内部流场和压力分布。周津炜等[6]用多孔介质模型代替换热器管束，对锅炉通流结构的流场进行了三维数值模拟，得出烟道内的流场分布，并分析了不同导流结构对流场的影响。但管束换热器导流结构参数对管束间流场均匀性影响的数值模拟还比较少见。而当三维换热器模型仅存在一维度变径，并且流体在某一维度上的流动不作考虑时，模型可以简化为二维形式。本次工作以二维叉排管束换热器模型为研究对象，运用CFD模拟，模拟了不同流速下换热器入口变径长度以及内导流结构进出口尺寸对换热器内部流场均匀性的影响，为同类型管束换热器导流结构优化提供了参考依据。

1 换热器几何模型与特征参数

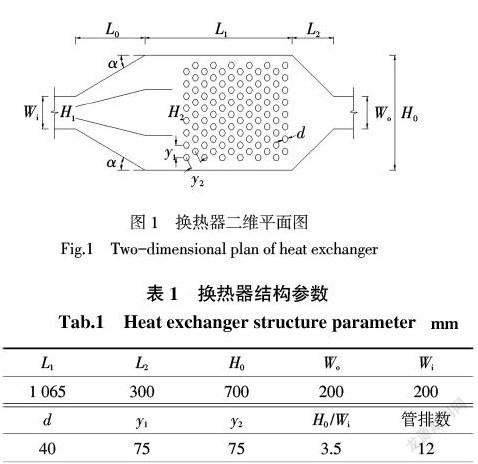
本次研究依托于实际工程项目，换热器为常用于锅炉烟气余热回收的管束式换热器，管束排列方式为叉排。如图1所示，其主要结构参数如表1。

换热器入口烟气实际流速为46 m/s，考虑到实际的烟气余热回收工程中，较少存在换热器入口烟气流速大于40 m/s的情况，因此选择15 m/s、30 m/s、46 m/s 3种入口流速，分别进行数值模拟。

换热器导流结构具有均布流体、强化传热等作用。从导流结构造价较低、阻力损失较小、加工安装便利等角度出发设计进口导流结构如图1 所示，为对称布置的两块隔板，这样布置的理想目标是：

1）流体经过导流结构入口后，两块导流隔板之间所夹流体流量为总流量的一半。

2）流体经过导流结构出口时，两块导流隔板之间流体流速与导流隔板之外流体流速相等。

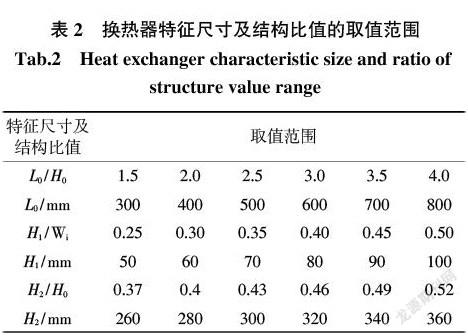
该导流结构的特征尺寸参数为：换热器进口变径长度L0、导流结构入口尺寸H1和导流结构出口尺寸H2。其中导流结构入口尺寸H1与换热器入口尺寸Wi的比值H1/Wi，导流结构出口尺寸H2与换热器主体尺寸H0的比值H2/H0，换热器进口变径长度L0与换热器主体尺寸H0的比值L0/H0是导流结构影响换热器内流场均匀性的关键参数。而且L0/H0的合理数值必然和换热器的换热器主体尺寸H0与换热器入口尺寸Wi的比值H0/Wi密切相关，这是由于L0的合理数值会随着Wi减小而增加，随着H0减小而减小。如图1所示，α为換热器入口倾斜度。

随着H0/Wi增大，要使得流场均匀，tan α必然要减小，于是给出公式（2）

经整理可得

式中：λ为换热器入口变径长度系数。

为了保证换热器流场均匀，导流的结构比值：H1/Wi，H2/H0以及L0/H0的最佳数值是本文的研究重点。而L0/H0的最佳数值可以转化为换热器入口变径长度系数λ的最佳数值研究。在模拟过程中，通过换热器的主体结构参数，确定进口导流结构特征尺寸及结构比值的取值范围如表2所示。

2 网格划分与模型设置

2.1 模型简化

1）本论文主要研究换热器内部流场均匀分布的情况，而流体对管束的侵蚀以及换热等不是研究重点，故将烟气用空气代替，且模拟过程中不考虑传热。

2）流场内流体为稳态流动。文献[8]和[10]指出，当雷诺数大于40的情况下横掠管束的流动在是非稳态的，但是在管间距比较小（<2）的情况下采用稳态模型仍可以得出准确的结果.本论文研究的换热器管束管间距比为1.625，因此换热器内部可视为稳态流动。

3）不考虑重力作用。模拟过程中由于气体为单相流，且空气密度小，水平流速大，可以忽略重力作用。

2.2 网格划分与无关化检验

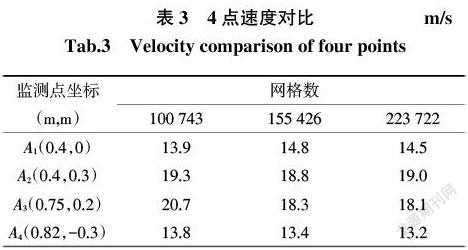
网格划分时，由于有多根管束，结构复杂，因此采用非结构网格，并进行网格无关化验证.以换热器入口流速V=46 m/s为例，采用相同网格划分方式，通过控制网格最大、最小单元尺寸，依次划分出网格总数为10万、15.5万、22万的模型，并在模型中选取4个点A1～A4，比较每个点在不同网格总数的模型下的速度差异，当速度差异小于5%时即可认为网格数量不再对计算结果产生影响[9]。

如表3所示，当网格数由15.5万增加到22万时，坐标点A1～A4的速度差异小于5%，即网格数在15.5万左右时，网格数量不再对计算结果产生影响。本次模拟选择网格总数为15.5万。

经模拟验证，此结论也适用于换热器入口流速V=30 m/s和V=15 m/s的情况。

2.3 求解器选择与边界条件设置

当马赫数大于0.3时，需要考虑流体的可压缩性;当马赫数小于0.3时，可视为不可压缩流体[9]。换热器内空气的声速按式（4）计算：

式中：k为空气的绝热指数，可取1.4;R为空气气体常数，287 J/（kg·K）;T为空气温度，可取烟气温度，即150 ℃。

通过计算，换热器内空气的声速为412.3 m/s。本模拟研究中换热器进口空气流速不高于46 m/s。换热器内最大马赫数Ma可按式（5）计算：

换热器内的空气流动的马赫数小于0.3，因此流体视为不可压缩流体，本文选用Fluent作为流场数值模拟的工具，选用压力基求解器。

在模拟过程中选择可实现k-ε模型[4]，近壁面模型选择标准壁面函数[7]。选择速度入口为边界条件，最大速度46 m/s。出口为自由出流边界条件。

3 气流分布均匀评价

为研究不同导流结构下流场的均匀性并方便比较，采用速度标准差来衡量换热器内部流场的均匀程度，从而得到换热器导流结构优化参数。

标准差S定义为

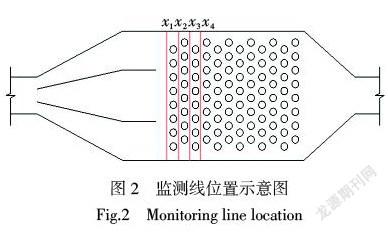
式中：vi为所取监测线上的各个节点流速（m/s）;v为监测线上所取各节点流速的算术平均值（m/s）;n为所取监测线的节点总数。监测线见图2。

本次研究，每条监测线均匀选取500个监测点。所取监测点数越多，越能准确反映监测线的流速分布情况，而通过多次模拟，当所取点数超过500时，监测线测点的速度标准差基本不变，故每条监测线选取500个监测点，即n=500。

由于流体横掠叉排管束，流体的扰动强烈，只要经过4排管子，流速就趋于均匀[5]，因此，如图2所示，在前4排管之前，取4根监测线x1～x4，分别计算每根监测线速度标准差，再取4个标准差平均值[S]。[S]越小，换热器内部流场越均匀，换热效果越好。

x1监测线与第1排管中心线间距为16.25 mm的4根监测线间距为32.5 mm。

4 计算结果及分析

采用控制变量法分别对换热器特征尺寸参数L0、H1、H2进行模拟，以速度标准差[S]为对比量，分析各参数与速度标准差的关系，速度标准差越小，换热器内部流场均匀性越好，换热性能越好。

4.1 入口变径长度系数λ对流场均匀性影响

取换热器导流结构入口尺寸H1=80 mm，导流结构出口尺寸H2 = 340 mm，换热器入口变径长度 L0 =300，400，500，600，700，800 mm，即λ = 0.34，0.46，0.57，0.69，0.80，0.91，分别模拟在不同入口流速下（V = 15 m/s、30 m/s、46 m/s）λ对流场均匀性的影响。

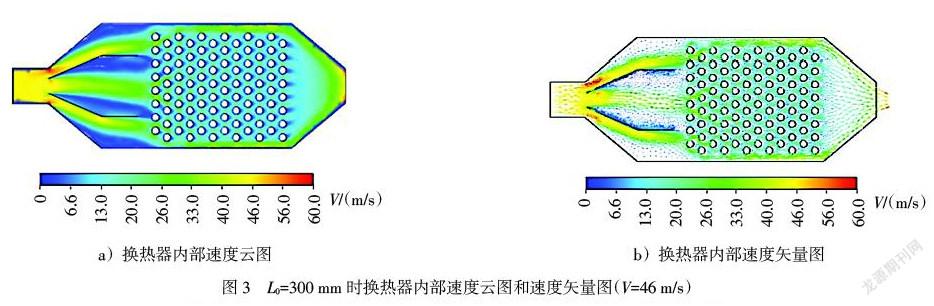
图3 a）、 b）分别为入口流速V = 46 m/s， L0 = 300 mm，即λ = 0.34时的速度云图和速度矢量图。圖3 b）中，流体在流出变径时出现涡旋，这是由于通过变径时通流面积突然扩大，气流发生转向，流动发生剧烈地紊流混合，边界层自换热器外壁分离并产生涡流区[6]。

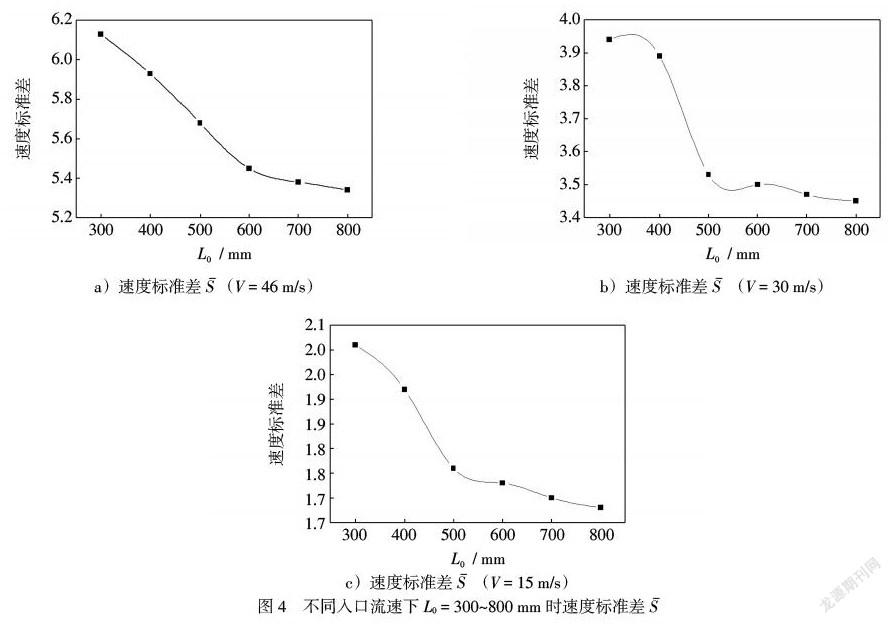
图4 a）、b）、c）分别为V=46 m/s、V=30 m/s、V=15 m/s时，[S]随L0变化的曲线图。从图4 a）中可以看出，L0=300～800 mm时，随着L0增加，换热器内部流场均匀性越好，但其均匀性增加幅度逐渐减小。L0从300 mm增加到600 mm时，L0每增加100 mm，流场均匀性提高，[∆S]约为0.2;L0从600 mm增加到700 mm时，[∆S]约为0.06;L0从700 mm增加到800 mm时，[∆S]约为0.04。可以推测，当L0增加到一定程度时，换热器内部均匀性基本不变。在实际工程中，考虑到换热器占地以及造价，为使换热器内部流场均匀，变径L0不宜过长，因此L0较优参数为600 mm，即换热器入口变径长度系数λ=0.69时，换热器内流场均匀性较好。

同理，由图4 b）、c）可以看出，当V=30 m/s和V=15 m/s时，L0较优参数为500 mm，即换热器入口变径长度系数λ=0.57时，换热器内流场均匀性较好。

由图4可得，相同换热器结构下，换热器内流场均匀性增加。[∆Smax]即[∆Smax]-[∆Smin]，随着换热器入口流速减小而减小，换热器入口变径的缓冲作用减弱，换热器入口变径长度系数最优值减小。

4.2 导流入口结构比值H1/Wi对流场均匀性影响

取换热器入口变径长度L0=600 mm，导流结构出口尺寸H2 = 340 mm，导流结构入口尺寸H1 = 60，70，80，90，100，110 mm，即H1/Wi = 0.25，0.30，0.35，0.40，0.45，0.50，分别模拟在不同入口流速下（V = 15、30、46 m/s），H1/Wi对流场均匀性的影响。

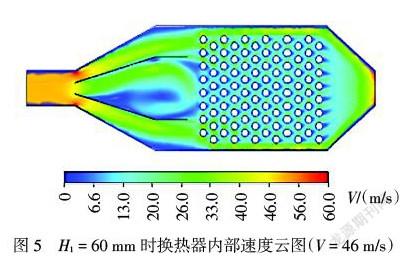
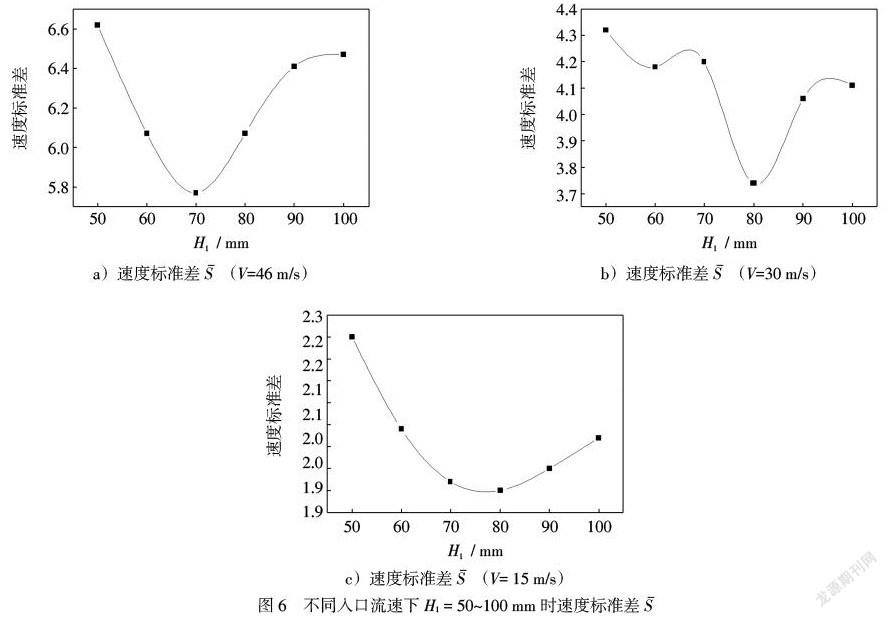
图5为入口流速V = 46 m/s，H1 = 60 mm，即H1/Wi = 0.25时的速度云图.图6 a）～c）分别为V = 46 m/s、V = 30 m/s、V = 15m/s时，[S]随H1变化的曲线图。由图6 a）可以看出，当H1 = 50～70 mm时，随着H1增加，换热器内部流场均匀性越好;当H1 = 70～100 mm时，随着H1增加，换热器内部流场均匀性越差。本次设置导流结构的目的是均分流体，而模拟结果是：在H1 = 70 mm，即导流入口结构比值H1/Wi = 0.35 ≠ 0.5时，换热器内部流场速度标准差[S]= 5.77为最低值，流场较为均匀。这是因为，流体内部质点间或流层间因相对运动而产生的内摩擦力使得流体之间存在粘滞性，从而使换热器入口的速度分布为抛物线，靠近换热器外壁的流体质点，粘附在外壁上，流速为零;位于轴线上的流体质点流速最大。因此，当导流入口结构比值H1/Wi = 0.35 < 0.5时，导流结构可以实现对流体较为均匀的分配，从而使得换热器内部流场均匀。

同理，由图6 b）、6 c）可以看出，当V = 30 m/s和V = 15 m/s时，H1较优参数为80 mm，即导流入口结构比值H1/Wi = 0.40时，换热器内流场均匀性较好。

随着换热器入口流速减小，入口轴线处流速与入口内壁处流速差值减小，从而需要增大导流入口结构比值H1/Wi，实现对流体较为均匀的分配，因此，随着换热器入口流速减小，导流入口结构比值最优值增加。而[ΔSmax]，即[Smax]-[Smin]的值随着换热器入口流速减小而减小。可以推测，随着入口流速逐渐减小，换热器结构对其内部流场均匀性影响逐渐减小。

4.3 导流出口结构比值H2 /H0对流场均匀性影响

取导流结构入口尺寸H1 = 70 mm，换热器入口变径长度L0 = 600 mm，导流结构出口尺寸H2 = 260，280，300，320，340，360 mm，即H2/H0 = 0.37，0.4，0.43，0.46，0.49，0.52，分别模拟在不同入口流速下（V = 15 m/s、30 m/s、46 m/s）H2/H0对流场均匀性的影响。

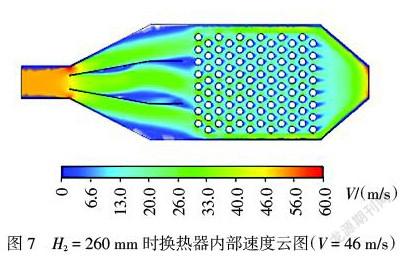
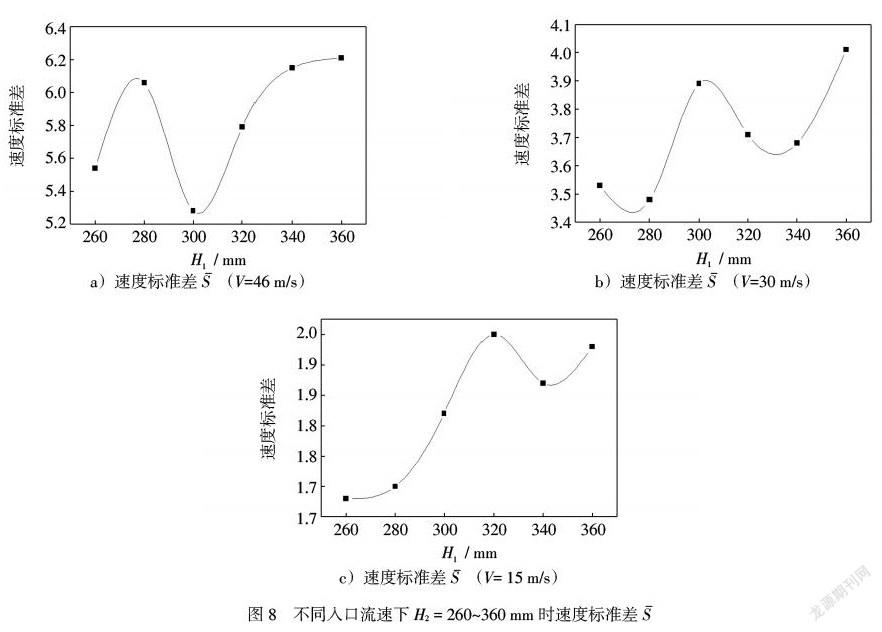
图7为V = 46 m/s ，H2 = 260 mm，即H2/H0=0.37时的速度云图。图8 a）～c）分别为V = 46 m/s、V = 30 m/s、V = 15 m/s时，[S]随H2变化的曲线图。由图8 a）可以看出，当H2 = 260～280 mm、H2 = 300～360 mm时，随H2增加，流场均匀性越好;当H2 = 280～300 mm时，随着H2增加，流场均匀性越差。当H2 = 300 mm，即导流出口结构比值H2/H0 = 0.43<0.5时，换热器内部流场较为均匀。

同理，由图8 b）、6 c）可以看出，当V = 30 m/s时，H2较优参数为280 mm，即H1/Wi = 0.40;当V = 15 m/s时，H2较优参数为260 mm，即H1/Wi = 0.37。

随着换热器入口流速减小，换热器导流出口结构比值最优值逐渐减小。

5 结论

采用计算流体力学方法，构建了管束式换热器二维简化模型，以速度标准差[S]为评价指标，研究了不同流速下换热器关键结构参数：换热器入口变径长度系数λ、导流入口结构比值H1/Wi以及导流入口结构比值H2/H0对换热器内部流场均匀性的影响，得到如下结论：

1）换热器变径长度L0越大，换热器内部流场均匀性越好，但当L0增加到一定程度时，换热器内部流场均匀性基本不变.实际工程中应考虑换热器占地及造价L0不宜过大。随着换热器入口流速减小，换热器内部流场越均匀，换热器入口变径的缓冲作用减弱，换热器入口变径长度系数λ最优值减小。

2）随着换热器入口流速减小，导流入口结构比值H1 / Wi最优值增加，导流出口结构比值H2 / H0最优值逐渐减小。当H1 / Wi、H2 / H0均小于0.5时，导流结构对流体均分效果较好，换热器内部流场更均匀。在使用相似导流结构均分流体时，可以使导流入、出口结构比值H1/Wi、H2/ H0取值小于0.5，从而得到较好的流体均分效果，使得流场更为均匀。

3）在相同换热器结构参数下，随着换热器入口流速减小，换热器内部流场越均匀。

随着换热器入口流速减小，[ΔSmax]，即[Smax]-[Smin]的值逐渐减小，换热器结构对其内部流场均匀性影响逐渐减小。

参考文献：

[1]    余徐飞，王治云，李起耘，等. 横掠周期性密集管束流动换热的数值模拟[J]. 上海理工大学学报，2015，37（6）：563-567.

[2]    张少华，程树森. 烟道内导流板的优化设计[C]//全国工业炉学术年会. 2006：123-128.

[3]    黄德斌. 气流横向冲刷管束换热数值模拟模型分析与数值求解[J]. 广东化工，2016，43（18）：39-40.

[4]    潘维，池作和，斯东波，等. 匀速流体横掠管束的流场数值模拟[J]. 浙江大学学报（工学版），2004，38（8）：1043-1046.

[5]    戴伟，刘应征. 横掠紧凑叉排管束流动的数值模拟与分析[J]. 制造业自动化，2011，33（2）：107-110.

[6]    周津煒，赵钦新，张知翔，等. 余热锅炉通流结构数值分析[J]. 华北电力大学学报，2011，38（2）：43-47.

[7]    刘敏珊，杨帆，董其伍，等. 流体横掠管束模拟中壁面函数影响研究[J]. 热能动力工程，2010，25（5）：497-500.

[8]    TAKEMOTO Y，KAWANISHI K，MIZUSHIMA J. Heat transfer in the flow through a bundle of tubes and transitions of the flow[J]. International Journal of Heat and Mass Transfer，2010，53（23/24）：5411-5419.

[9]    王庆锋，郝帅，李凯，等. 基于CFD数值模拟的换热器外导流筒优化设计[J]. 过程工程学报，2017，17（3）：461-468.

[10]  陈作义. 空气横掠正方形排列管束的对流换热数值模拟[J]. 广东二师范学院学报，2012，32（5）：52-56.

[责任编辑 田 丰]