含风电的区域综合能源系统运行优化研究

张江华　黄云峰　奚培锋

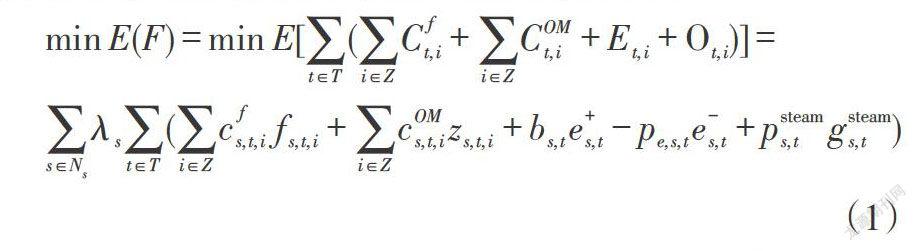
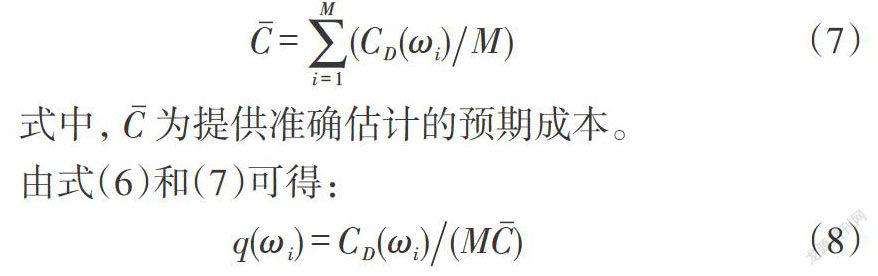
摘 要：本文通过考虑风电输出功率的预测误差具有不确定性的特点，采用重要性采样场景生成方法，探讨含风电的区域综合能源系统运行优化，并通过仿真实验验证了所提出方法的有效性。结果表明，本文提出的方法具有更好的经济性、稳定性和可靠性。

关键词：区域综合能源系统;运行优化;场景分析;风力发电

中图分类号：M614;TM732 文献标识码：A 文章编号：1003-5168（2019）35-0148-03

Study on Operation Optimization of Regional Comprehensive

Energy System with Wind Power

ZHANG Jianghua1 HUANG Yunfeng1 XI Peifeng2

（1.School of Automation Engineering， Shanghai University of Electric Power，Shanghai 200090;2.Shanghai Smart Grid Demand Response Key Laboratory，Shanghai 200063）

Abstract： In this paper， by considering the uncertainty of the prediction error of wind power output， the importance sampling scenario generation method was adopted to explore the operation optimization of regional integrated energy system with wind power， and the effectiveness of the proposed method was verified by simulation experiments. The results show that the proposed method has better economy， stability and reliability.

Keywords： regional integrated energy systems;operation optimization;scenario analysis;wind power generation

在含有大规模风电的区域综合能源系统中，虽然对风电功率的预测做了大量研究工作，但风功率预测误差的存在，使风电的不确定性对区域综合能源系统运行优化有着重要影响[1]。实际上，风力发电本身具有不确定性和较强的波动性特点，其影响不可忽略。而用蒙特卡洛模拟法模拟风力发电需要利用大量的样本空间，大大降低了运算速度。

由于场景分析法能明确体现风电不确定性的概率特征，并可向上建立随机规划模型，因而成为随机机组组合问题处理风电不确定性的主要方法之一[2]。场景分析方法在描述带有不确定性分布式可再生能源的区域综合能源优化运行问题时，能将其不确定性转化为确定性的混合正式非线性问题。

本文在现有的含热电联产的区域综合能源系统运行分析模型基础上，进一步考虑风电输出功率的预测误差具有不确定性的特点，采用重要性采样场景生成方法，并与基于概率的场景分析方法进行比较分析。

1 区域综合能源系统的随机运行优化模型

1.1 目标函数

区域能源系统运行优化问题的目标函数为区域能源系统运行成本最小。其中，运行成本为系统机组发电、启停成本及产蒸汽成本。目标函数可表示为：

[minE（F）=minE[t∈T（i∈ZCft，i+i∈ZCOMt，i+Et，i+Ot，i）]=s∈Nsλst∈T（i∈Zcfs，t，ifs，t，i+i∈ZcOMs，t，izs，t，i+bs，te+s，t-pe，s，te-s，t+psteams，tgsteams，t）]（1）

式中，[E（F）]表示總的系统运行成本的期望值;[t]为调度周期[T]的一个时间段;[Z]为系统中的机组集合;[Cft，i]为[t]时间段内机组[i]的燃料成本;[COMt，i]为[t]时间段内机组[i]的运行操作成本;[Et，i]为[t]时间段内机组[i]对大电网的出口而产生的收益;[Ot，i]为[t]时间段内机组[i]对热网出口蒸汽而产生的收益;[Ns]为情景数量;[λs]为情景[s]下对应的概率;[cfs，t，i]为机组运行需要的燃料价格;[fs，t，i]为机组运行所需要的燃料;[zs，t，i]机组启停状态;[bs，t]为系统向大电网购买电的价格;[e+s，t]为系统向大电网购买的电量;[pe，s，t]为系统向大电网售卖电的价格;[e-s，t]为系统向大电网售卖的电量;[psteams，t]为系统售卖蒸汽的价格;[gsteams，t]为系统售卖的蒸汽量。

1.2 约束条件

①系统电力平衡约束为：

[t∈T[i∈Z（egeni，t，s-econi，t，s）+e+t，s-e-t，s]=t∈TDet]            （2）

式中，[egeni，t，s]为系统机组的产电量;[econi，t，s]为系统自身用电量;[Det]为[t]时间段的系统电负荷量。

②系统热平衡约束为：

[t∈T（wt，s+αwt-1，s+i∈Zhgeni，t，s）=t∈TDht]              （3）

式中，[hgeni，t，s]为机组蒸汽产量;[wt，s]为t时间段内蒸汽储量;[α]为蒸汽热损;[Dht]为[t]时间段的系统热负荷量。

③机组启停约束为：

[Δzi，t，s≥zi，t，s-zi，t-1，sΔzi，t，s≤1-zi，t-1，sΔzi，t，s≤zi，t-1，st∈TΔzi，t，s≤Ni，s]                     （4）

式中，[Δzi，t，s]为机组启停的变化量;[zi，t，s]为机组启停状态，为二进制变量;[Ni，s]为系统允许最大机组开启量。

④储能设备约束为：

[Wmint，s≤wt，s≤Wmaxt，sΔwmint，s≤wt，s-wt-1，s≤Δwmaxt，s]          （5）

式中，[Wmint，s]、[Wmaxt，s]为储能设备的最小、最大储蓄量;[Δwmint，s]、[Δwmaxt，s]为储能设备在[t]时间段内储能变换的最小、最大量。

2 重要性场景分析方法

重要性场景分析方法是一种基于风力发电预测场景经济分配问题运营成本的概率重要性抽样方法。Bruninx K等[3]提出了一种基于重要性抽样的情景算法，通过将其与一个具有大量场景的随机公式进行比较，发现使用重要性场景方法，可以把随机机组组合转化为确定性机组。主要过程如下：

给定场景集合[ΩS={ω1，ω2，…，ωM}]和场景概率分布[p]，并给定场景重要性度量[q]，其表示对目标函数[C]权重的无偏估计。理想情况下，[q]代表场景调度结果对预期值的影响，即

[q*（ω）=p（ω）C（ω）EpC]                              （6）

式中，[Ep]表示场景概率分布[p]的期望。由于[EpC]是最终的计算量，因此场景重要性度量[q*（ω）]采用通过少量场景的结果计算近似估计度量[q]的方法。假设场景集合为[ΩS]，原始测量[p]为均匀分布在[ΩS]上，所以[p（ω）=M-1]，其中[ω∈ΩS]。当每个场景相对于确定性问题的目标函数为[CD（∙）]时，得到的等式为：

[C=i=1M（CD（ωi）M）]                              （7）

式中，[C]为提供准确估计的预期成本。

由式（6）和（7）可得：

[q（ωi）=CD（ωi）（MC）]                             （8）

重要性场景分析是一种解决由风电功率预测误差的不确定性引起的综合能源系统运行优化问题的有效方法，将模型中的不确定性问题变成多个确定性问题的集合，从而方便建立模型，优化计算方法。

3 算例分析

3.1 算例系统构成

综合能源系统结构如图1所示。

图1 综合能源系统结构

3.2 场景设计

假设光伏发电的预测输出数据已知，根据“预测箱”方法产生1 000个光电场。然后估计每个场景对应的含光电问题目标函数值，用重要性采样方法对场景样本进行选择，通过后项场景缩减对1 000个光电场景进行消减，消减至10个场景，再将10个场景的风电输出功率，通过综合能源系统一般化模型求解机组的启停时序，将结果作为日内经济调度的输入，可得到各个机组的运行方案及运行成本。表1为24h内各个机组的启停状态运行方案。

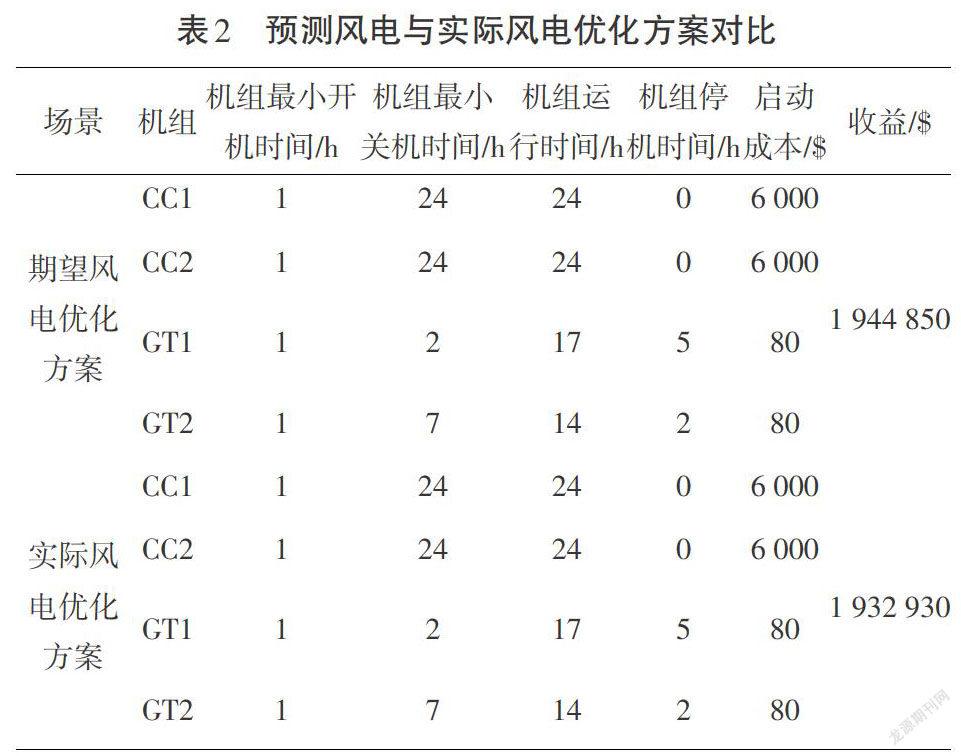
将优化方案运用到当日实际风电输出场景中，可以得到如表2所示的结果。

由表2可知，根据重要场景分析方法及代理模型优化计算后得到的优化方案适用于实际风电量。整体收益与期望最大收益相比变化不大，说明该运行方案可作为当前调度方案。该方案在两种场景下具体机组的产出如图2和图3所示。

表1 日内调度各机组运行方案

注：1表示开启，·表示该时间段机组关闭。

表2 預测风电与实际风电优化方案对比

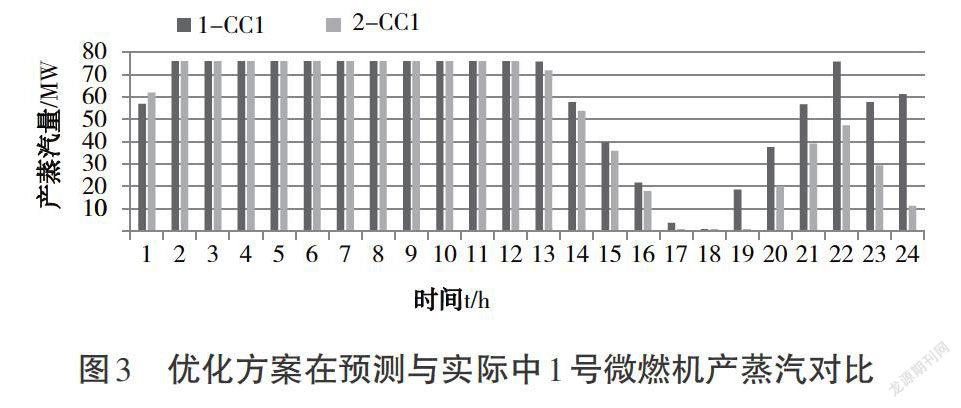
由图2和图3可知，各个时刻，各机组无论是产电量或者产蒸汽量，都较为接近，最大程度上满足了负荷需求，同时又提高了综合系统运行的经济效益。

4 结语

本文采用场景分析法来刻画风电的不确定性，并提出用重要性采样方法对场景进行分析。与传统的场景生成方法相比，该方法在不降低准确性的条件下，计算成本较低。随后，以上海某园区的含风电综合能源系统为研究对象，验证了模型的可行性和计算方法的有效性。结果亦表明，通过优化模型得到的运行方案在不同风电输出的场景下灵活调整，提高了综合系统经济性，同时也降低了风电输出波动性给电网带来的影响，具有较好的稳定性和可靠性。

图2 优化方案在预测与实际中1号联合机组产电量对比

图3 优化方案在预测与实际中1号微燃机产蒸汽对比

参考文献：

[1] Louka P， Galanis G， Siebert N， et al. Improvements in wind speed forecasts for wind power prediction purposes using Kalman filtering[J]. Journal of Wind Engineering & Industrial Aerodynamics，2008（12）：2348-2362.

[2] Zhang Z， Sun Y， Li G， et al. A solution of economic dispatch problem considering wind power uncertainty[J]. Automation of Electric Power Systems，2011（22）：125-130.

[3]Bruninx K， Delarue E. Scenario reduction techniques and solution stability for stochastic unit commitment problems[C]//Energy Conference.IEEE，2016.