基于复合型进化算法的地下水污染反演模型
黄林显 刘治政 邢立立 杨丽芝 朱恒华 纪纹龙 张永勇

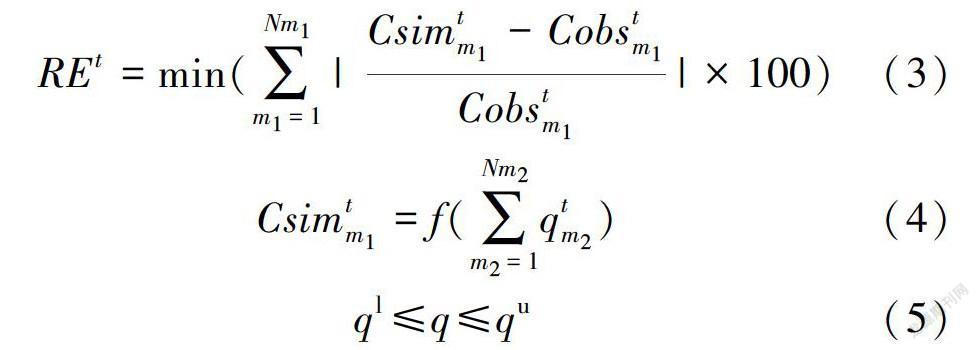
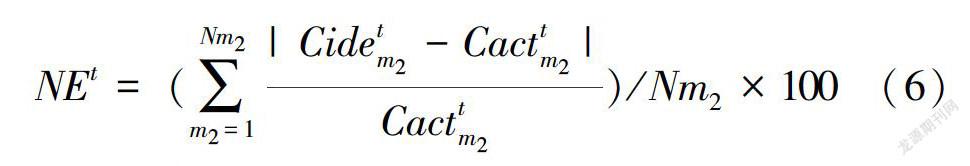



摘要:污染源位置和污染物排放浓度的快速确定直接决定着地下水污染的有效治理及修复,这属于地下水反演问题。通过充分分析地下水污染反演问题,耦合地下水流模拟程序MODFLOW、溶质运移模拟程序MT3DMS和优化算法SCE-UA,设计了一种模拟一优化( S/O)反演模型。通过实例验证,反演结果表明:提出的网格遍历CT算法可以自动验证潜在污染区内所有可能的污染源位置组合方式:与传统地下水污染反演模型相比,S/O模型不但能够适用于稳定流条件,而且适用于非稳定流条件;所开发的S/O模型对于多污染源分别在稳定流和非稳定流下的反演均有非常高的精度,能够准确反演污染源位置及污染物排放浓度。
关键词:地下水污染;污染源位置:SCE-UA优化算法;S/O模型
中图分类号:P641.2
文献标志码:A
doi:10.3969/j.issn. 1000- 1379.2019.04.013
地下水一旦遭受污染,其治理不但投入巨大,而且耗时长[1-3]。地下水污染防治的关键是及时确定污染源的位置,从而采取措施切断污染途径,并进行针对性修复,避免更大范围的污染发生。如何快速、准确定位污染源位置和污染物排放浓度,已成为地下水科研领域一个非常重要的研究方向,这属于地下水反演问题。国内外学者对地下水污染反演问题进行了大量研究:Prakash等[4]通过优化设计监测点网络布局,利用污染物浓度的变化进行地下水污染源识别:Gorelick等[5]分别将最小二乘法、线性规划法等与溶质运移模型结合,对比了两种方法运用于地下水污染物运移特征识别的优缺点:Foddis等[6]设计了一种借助人工神经网络( ANNs)的优化反演模型,并将其应用于均质各向同性二维含水层反演中:江思珉等[7]采用Hooke -Jeeves吸引扩散粒子群混合算法、和声搜索算法等对地下水污染物释放强度进行了反演:顾文龙等[8]将污染源反演过程转化为贝叶斯推理过程,并与克里格替代模型结合,提出了一种反演地下水污染源释放浓度的新思路。此外,自适应模拟退火算法(ASA)[9]、自适应多尺度方法10]、正态转换一集合卡尔曼滤波法( NS-EnKF)[11]和蒙特卡洛[12]等方法也被应用于地下水污染反演问题的求解中。
上述方法虽然从不同角度对地下水污染反演问题进行了探讨,并取得了很多成果,但也存在一定局限性。如监测点网络优化布局法需要大量监测井的监测数据,采样和测试过程耗费大量人力和财力,且只能大致确定污染源的方向,不能快速精确定位:传统的最小二乘法、线性规划法等,当研究区水文地质条件比较复杂时,反演过程容易陷入局部搜索,得不到全局最优解,影响反演精度:地质统计学方法的反演精度取决于对研究区的了解程度,当未知变量较多时,计算量大,且容易出现病态矩阵问题:近几年兴起的全局最优解启发式搜索方法如人工神经网络法等,需要大量数据进行样本训练,如果不能实现地下水流模型、溶质运移模型和优化算法的有效耦合,那么会引起计算过程的复杂化,增加计算负担,或者只能模拟稳定流,不能模拟非稳定流,限制了其使用范围。此外,对于一些传统反演优化方法,需要已知污染源位置才能对排放浓度进行反演,而实际应用中污染源的位置是不确定的,或者只能确定在某一个范围内,这限制了此类方法的应用。
基于以上分析,本文提出了一种基于全局搜索SCE-UA算法的模拟一优化S/O反演模型,并进行不同案例情况下的反演验证。该模型采用SCE-UA优化算法,能够更加有效、快速搜索全局最优解,避免了传统优化算法容易早熟收敛、陷入局部最优解的弊端,鲁棒性好。通过采用FORTRAN语言编写接口程序,实现了地下水数值模拟程序MODFLOW(地下水流模拟程序)和MT3DMS(溶质运移模拟程序)与优化算法SCE-UA的对接,使得数据交换由传统的文件读取改進为内部变量传递,有效减小了计算负担,且能够适用于多污染源、稳定流和非稳定流等各种复杂情况。同时,提出了一种网格遍历GT算法,可以在没有或者只有很少关于污染源位置信息的情况下,通过验证潜在污染区所有可能污染源的位置组合方式,对污染源进行精确定位。
1 方法原理
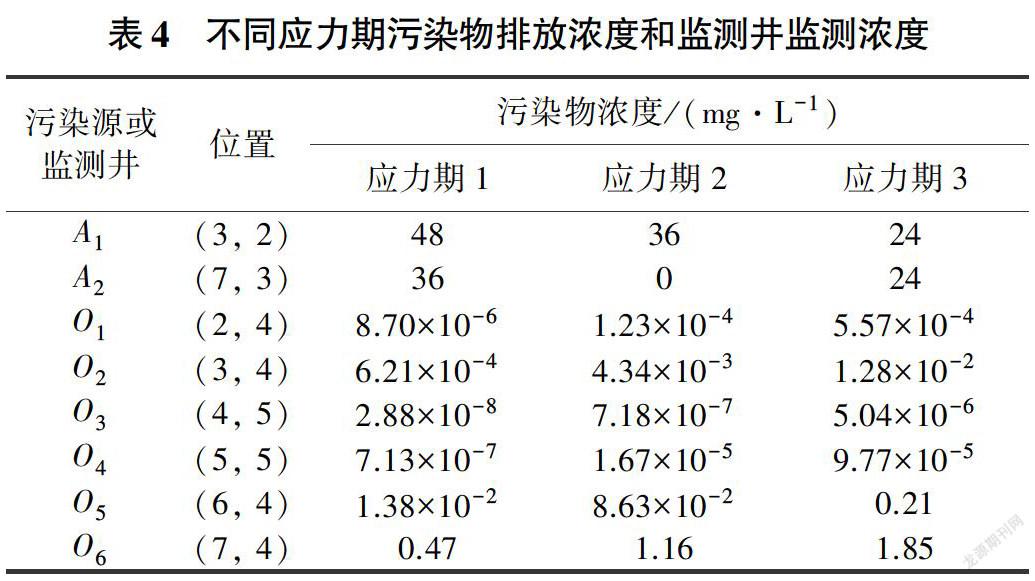
S/O反演模型利用MODFLOW和MT3DMS模拟污染物在地下水中的运移过程:SCE -UA优化算法根据观测井处污染物浓度模拟值和观测值的标准化差值NE,通过反射、变异和进化对污染源的污染物排放浓度进行反演:GT算法通过所设计的网格遍历算法快速、有效地搜索研究区内所有可能的污染源位置组合,最终达到准确确定污染源位置、浓度以及污染物排放过程的目的。3个模块通过FORTRAN程序实现相互之间的链接,并通过变量传递实现数据交换。S/O反演模型的主要结构及不同模块之间的链接见图1(其中BAS、RIV和LPF等分别为MODFLOW和MT3DMS的子程序包)。
1.1 地下水控制方程
(1)地下水流动方程。根据质量守恒、能量守恒以及Darcy定律,不考虑水密度变化条件下,孔隙介质中地下水在三维空间流动的偏微分方程为[13]
研究中,地下水流模拟程序MODFLOW和溶质运移模拟程序MT3DMS被联合使用,以模拟求解污染物运移的时空分布状况。
1.2 SCE-UA算法
SCE-UA算法是一种全局搜索优化算法,最初由美国亚利桑那大学的Duan等在1992年提出。该算法可以有效解决地下水污染物运移强烈非线性特征所带来的早熟收敛、容易陷入局部最优解等弊端,能够快速搜索到全局最优解,且稳定可靠,较其他算法具有一定优越性。SCE-UA算法综合了单纯形法、随机搜索和生物竞争进化等方法的优点,引人种群概念,复合形点在可行域内随机生成,并根据生物进化规则不断优化[15-16]。
1.3 遍历寻优(GT)算法
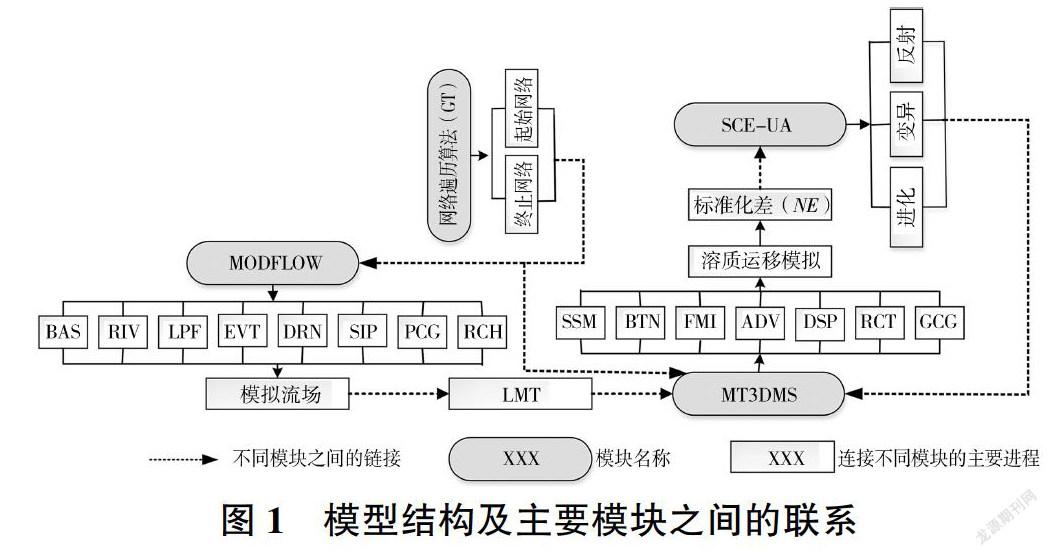
进行地下水污染源反演时污染源的位置往往是未知的。解决此类问题通常的做法是通过实地调查和查阅有关资料预先划定一个潜在子区域,确保所有可能的污染源组合落在这个子区域中,见图2。
本次研究开发了一种可以自动搜索预定义子区域中多个污染源所有可能位置组合的网格遍历GT算法。在GT算法中,开始单元格分别通过行、列、层号索引变量Rmin、Cmin、Lmin界定预定义子区域的上边界,结束单元格分别通过行、列、层号索引变量Rmax、Cmax、Lmax界定预定义子区域的下边界,所有可能的污染源组合通过以上6个变量遍历。整个搜索过程通过FORTRAN语言编写的计算机程序进行,并与S/O优化模型链接。对于非稳定流问题的反演,GT算法将遍历每一个应力期内所有污染源位置的组合,并通过判断目标函数RE值来获得最优解。反演问题的复杂性随着污染源个数的增加而增加,例如预定义子区域包含16个单元格,如果只有1个污染源,那么可能的污染源位置为16个;如果污染源的个数是2个,那么可能的污染源位置组合为120个:如果污染源的个数是3个,那么可能的污染源位置组合为560个。
2 模拟一优化模型
2.1 目标函数及标准化差公式
S/O模型在反演过程中通过目标函数RE值调整SCE-UA算法中种群的进化,通过标准化差值NE检验反演结果的精确性和鲁棒性。
(1)目标函数。目标函数用来判断监测井实测污染物浓度与S/O模型模拟污染物浓度的吻合程度,目标函数的选择对反演结果的优劣至关重要,它是SCE-UA算法进化寻优的基础。目标函数定义为
(2)标准化差公式。为了检验S/O反演模型的精度和鲁棒性,引入了标准化差公式。假设污染源污染物排放浓度真实值Cact已知,可以通过MODFLOW和MT3DMS计算监测井处的浓度Cobs:假设Cact未知,可以通过监测浓度Cobs和S/O模型反演污染源污染物排放浓度Cide。S/O模型的反演精度可以通过以下标准化差公式进行衡量:
2.2 S/O模型结构
S/O模型可以划分为模拟模型和优化模型两部分。模拟模型包含地下水流模拟程序MODFLOW和溶质运移模拟程序MT3DMS.主要用来模拟地下水流和污染物的有关运移特征:优化模型主要通过SCE -UA优化算法产生种群样本点(污染源污染物浓度值),并根据RE值进行变异、反射和进化样本点值,在全局范围内搜索可能的污染源位置和污染物排放浓度,最终达到快速、准确锁定污染源位置和污染物浓度的目的。需要注意的是当RE值为0时,说明反演的污染源位置和污染物浓度值与真实情况完全一致,但由于实际操作过程中模拟误差和观测误差的存在,因此这种情况很难发生。GT遍历算法通过自动搜索所有可能的污染源位置.提高了S/O优化模型的反演效率和准确度。地下水模拟模型、优化模型和GT算法通过FORTRAN语言编写的接口程序内部链接,使得数据交换由传统的文件读取转化为内部变量传递,极大提高了计算效率。
地下水模拟模型和优化模型的链接:①SCE -UA算法和接口程序重设MODFLOW和MT3DMS的相关输入文件,如WEL、SSM和BTN文件等。②MODFLOW和MT3DMS模拟计算监测井污染物浓度,并与监测浓度相比较,计算RE值,如果RE值小于收敛指标,认为反演值与实际情况一致,则进行下一个应力期的反演:如果RE值大于收敛指标,SCE -UA算法根据RE值,通过变异、反射和进化对污染源污染物浓度值优化,继续重设MODFLOW和MT3DMS的相关输入文件。在一个应力期内当所有可能的污染源位置都通过GT算法被验证后,反演过程将会移向下一个应力期。S/O模型链接过程见图3。
3 案例研究
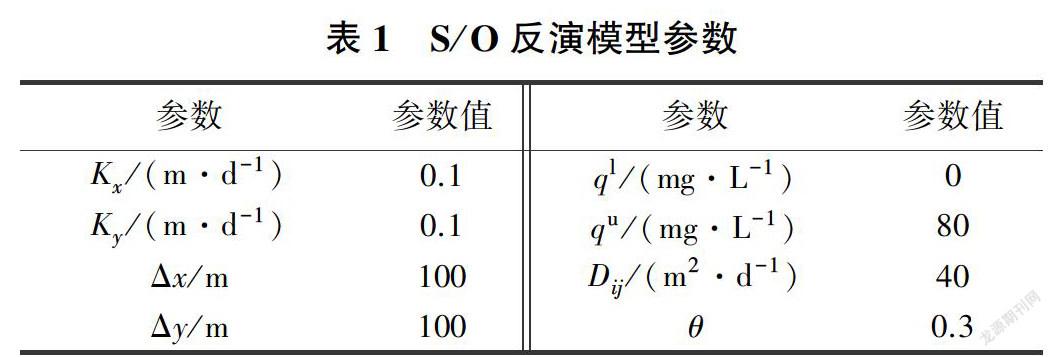
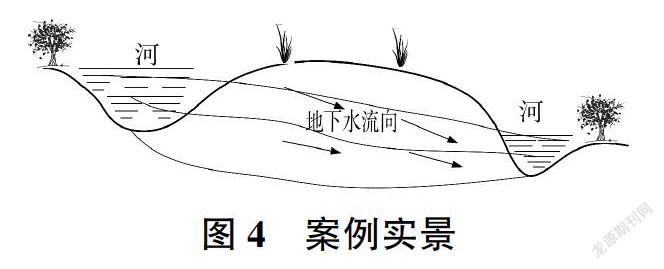
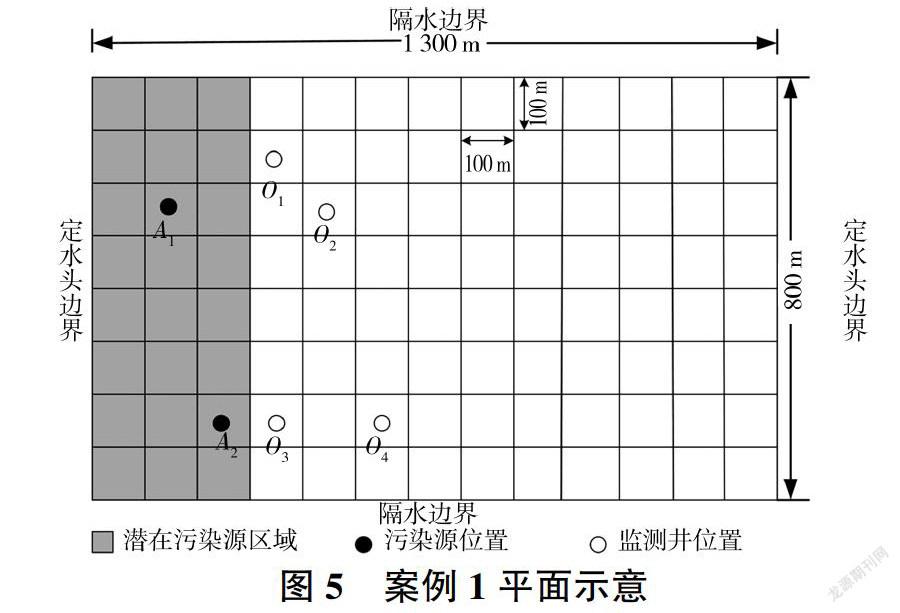
S/O反演模型的反演效果分别通过以下两个案例进行验证:案例1为稳定流条件,有两个污染源但位置未知,只知道可能存在的范围,通过4个监测井的监测浓度值反演污染源的位置和污染物浓度排放值:案例2更接近于实际情况,为包含3个应力期的非稳定流条件,有两个位置未知的污染源,且污染源污染物排放浓度在每个应力期均不相同,通过6个监测井的监测浓度值反演不同应力期污染源的位置和污染物排放浓度。案例研究参考RAJ等[17]进行地下水污染源反演验证时所设计的模擬河间地块地下水流动情况的实例模型(见图4)。本次案例研究的主要目的是评价S/O模型的反演效果,因此在地下水数值建模时对研究区水文地质条件进行了一定程度的概化。数值模型在横向上剖分成规格为100 mxl00 m的正方形网格,纵向上剖分为1层。模型区东、西边界分别为给定水头边界(东边界为88 m,西边界为100 m),南、北边界分别为隔水边界。S/O模型相关参数见表1。
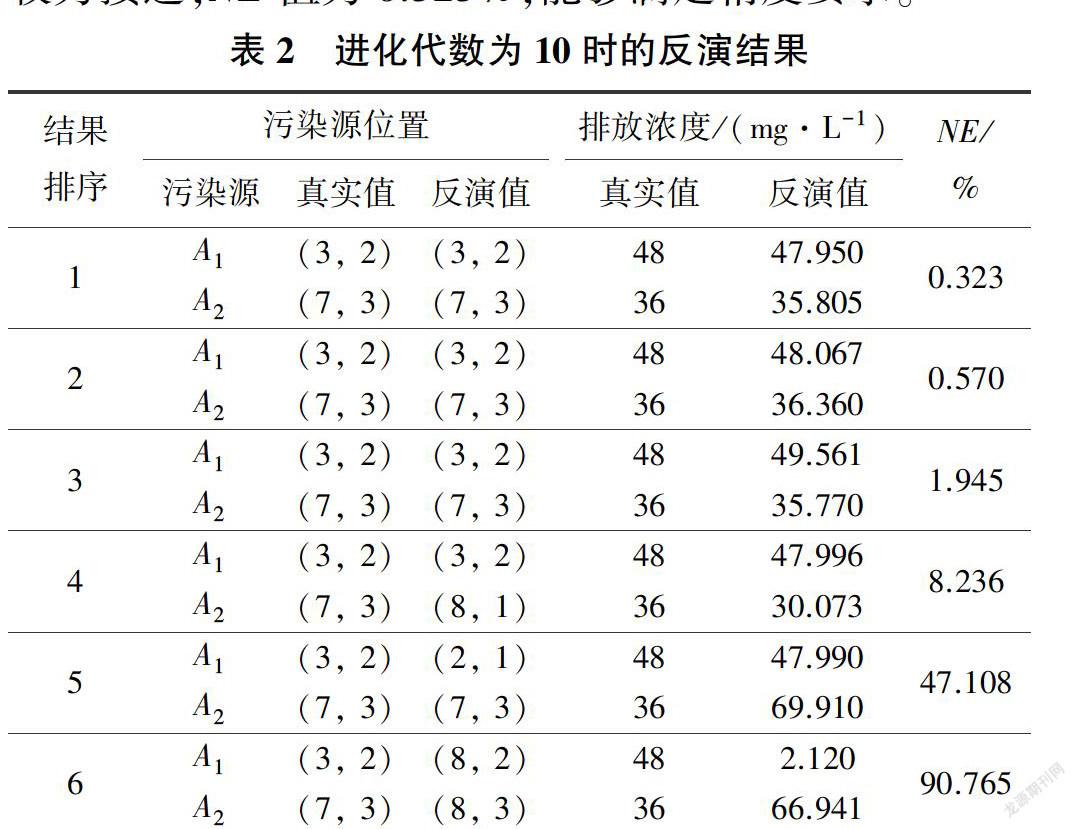
SCE-UA算法进化代数为10时的反演结果见表2。需要注意是,由于276个位置组合需要被搜索,因此在实际反演过程中产生了很多结果,表2仅仅根据NE值选取了几组具有代表性的结果进行展示。从表2可以看出,真实污染源的位置可以从276个可能的位置组合中被准确搜索出来,如结果排序1-3,且反演结果最好时两个污染源污染物排放浓度分别为47.950mg/L和35.805 mg/L,与真实值48 mg/L和36 mg/L较为接近,NE值为0.323%,能够满足精度要求。
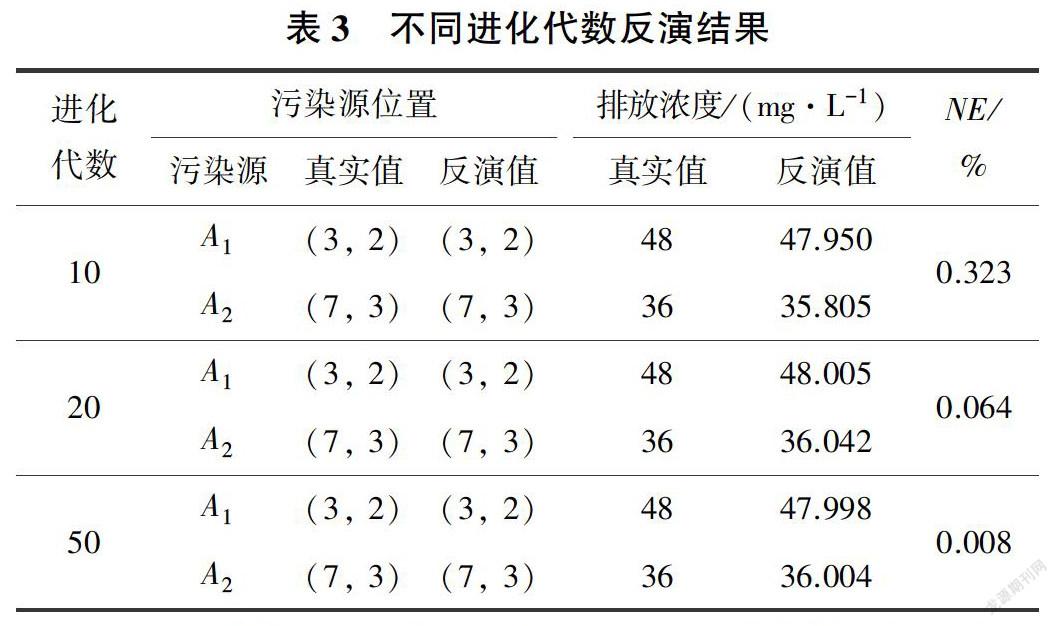
从表2可以看出,当反演位置正确的时候,反演的浓度值均较接近真实值,NE值为0.323% -1 .945%.基本满足精度要求:但当反演位置不准确时,反演的污染物浓度值与真实值差别很大,NE值为8.236% -90.765%.不能满足精度要求,因此可以看出污染源位置的准确确定是污染物浓度反演成功的前提条件。此外,对进化代数对反演结果的影响进行了测试,从表3可以看出,当进化代数分别为10、20和50时,反演结果与真实值均非常接近,NE值为0.008% - 0.323%,完全能够满足精度要求。同时,随着进化代数的增加,NE值逐渐减小,说明反演精度提高。但需要注意的是,进化代数的增加会带来很大的计算负担,反演时间会成倍增加。
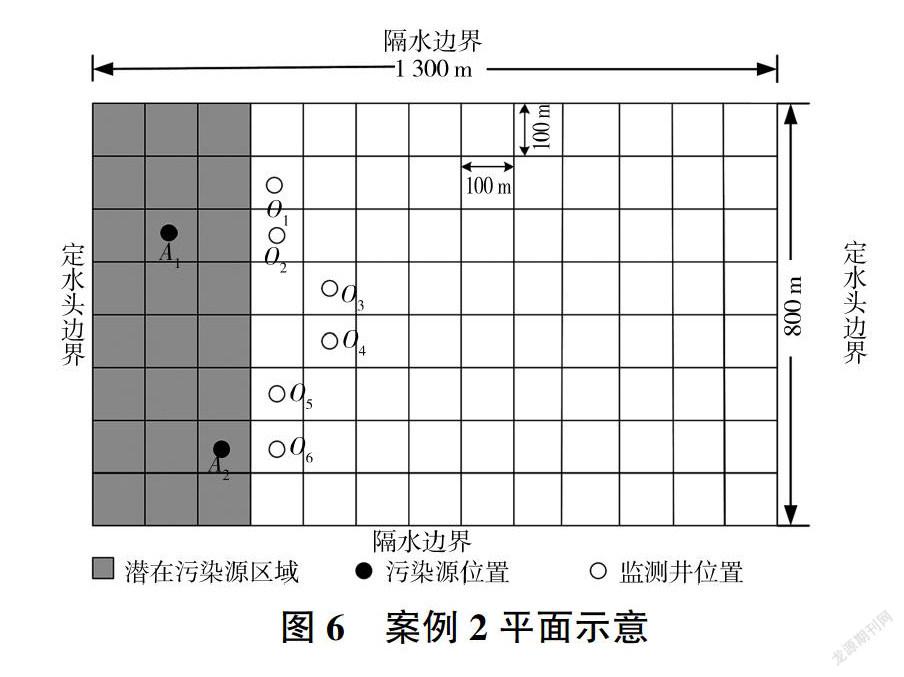
(2)案例2。现实中污染物的运移往往是在非稳定流条件下进行的,并且不同应力期的排放浓度是变化的。在案例2中,对具有3个应力期(应力期为la)的非稳定流情形进行验证。污染源的真实位置分别位于A1(行=3、列=2)和A2(行=7、列=3),且假设未知,可能的位置位于图6阴影区域。6个监测井分别位于01(行=2、列=4)、02(行=3、列=4)、O3(行=4、列=5)、O4(行=5、列=5)、05(行=6、列=4)、06(行=7、列=4)。每个应力期的真实浓度和监测浓度见表4。
由于案例2有3個应力期,因此每个应力期都需要搜索276个可能的位置组合。S/O反演模型在处理非稳定流问题时,当前应力期反演的进行要基于前面应力期的反演结果:反演第一个应力期并获得污染源位置和污染物排放浓度的最优解:第二个应力期的反演,首先运行第一个应力期反演的最优解,然后再反演第二个应力期并获得最优解;第三个应力期以此类推。所以,本应力期的反演结果取决于前面应力期反演结果的准确性,NE值也会因前面应力期反演误差的累积而不断增大。
当进化代数为10时,每个应力期的最优反演值见表5。从表5可以看出,第一个应力期NE值是2.91%,反演结果尚在可以接受的精度范围内,但随着应力期的增加,NE值在第三个应力期增大为58.00%(第二个应力期由于A2点污染物排放浓度为0,因此NE值无法计算),且反演的位置与真实位置不一致。为了获得更准确的反演结果,把进化代数分别增加为20和50,反演结果见表6。
从表6可以看出,当进化代数为20时,只有前两个应力期能够获得可以接受的结果,到第三个应力期,反演结果与真实值相差较大;当进化代数为50时,全部3个应力期污染源位置和污染物排放浓度反演值都与真实值较为接近,能够获得令人满意的结果。由此可以得出:通过增加进化代数.S/O反演模型的反演精度可以得到提高;随着非稳定流应力期的增加,需要相应增加进化代数以获得更加准确的反演结果。
4 结语
在已知监测井监测浓度的情况下推求污染源位置和污染物排放浓度是典型的地下水数值模拟反演问题。反演过程中可转化成决策变量为污染源位置和污染物排放浓度的最优化问题进行求解。将优化算法SCE - UA和地下水数值模拟程序MODFLOW和MT3DMS结合起来,建立了S/O优化搜索模型。
(1)通过接口程序,实现了SCE -UA优化算法和MODFLOW、MT3DMS的链接,使得数据交换由文件读取改进为内部变量传递,不但大大提高了S/O反演模型的计算效率,而且使其同时具备在稳定流和非稳定流条件下反演的能力。
(2)稳定流案例研究表明,S/O优化模型对于双污染源、污染源位置未知情况下的反演,能一致、高效地收敛到全局最优解,收敛速度较快、稳定性好,在进化代数较少的情况下就可以实现对污染源位置和污染物排放浓度的准确反演。
(3)对于非稳定流案例研究表明,S/O优化模型的反演误差会随着应力期的增加不断累积,但通过增加进化代数,同样可以获得令人满意的反演结果,能够对污染源位置和污染物排放浓度进行精确反演。
(4)随着应力期和进化代数的增加,计算负担不断加大,计算时间甚至是以天或月计,下一步要重点研究并行算法在S/O反演模型中的应用,以进一步提高计算效率,并采用更加接近实际情况的实例模型进行验证,使S/O反演模型更加具有实用性。
参考文献:
[1]KANEL S R,MALLA G B,CHOI H.Modeling and Study ofthe Mechanism of Mobilization of Arsenic Contamination inthe Croundwater of Nepal in South Asia[J].Clean Technol-ogies and Environmental Policy, 2013, 15(6):1077-1082.
[2]DUCCI D, SELLERINO M.Vulnerability Mapping ofCroundwater Contamination Based on 3D LithostratigraphicalModels of Porous Aquifers[J].Science of the Total Environ-ment, 2013, 447: 315-322.
[3]江思珉,王佩,施小清,等,地下水污染源反演的Hooke -Jeeves吸引扩散粒子群混合算法[J].吉林大学学报:地球科学版,2012,42(6):1866-1872.
[4] PRAKASH 0, DATTA B.Optimal Monitoring NetworkDesign for Efficient Identification of Unknown CroundwaterPollution Sources[ J]. Intemational Journal of Ceomate,2013, 23( 10): 2031-2049.
[5] CORELICK S M, EVANS B,REMSON I.IdentifyingSources of Croundwater Pollution: an Optimization Approach[J]. Water Resources Research, 1983, 19(3): 779-790.
[6] FODDIS M L,ACKERER P,MONTISCI A, et al.ANN-based Approach for the Estimation of Aquifer PollutantSource Behavior[J].Water Science and Technology: WaterSupply, 2015, 15(6):1285-1294.
[7] 江思珉,蔡奕,王敏,等,基于和声搜索算法的地下水污染源与未知含水层参数的同步反演研究[J].水利学报,2012,43( 12):1470-1477.
[8] 顾文龙,卢文喜,张宇,等,基于贝叶斯推理与改进的MCMC方法反演地下水污染源释放历史[J].水利学报,2016,47(6):772-779.
[9] JHA M, DATTA B.Three-Dimensional Croundwater Con-tamination Source Identification Using Adaptive SimulatedAnnealing[J].Journal of Hydrologic Engineering, 2012, 18(3):307-317.
[10]MAJDALAM S,ACKERER P.Identification of CroundwaterParameters Using an Adaptive Multiscale Method[J].Ground-water, 2011, 49(4): 548-559.
[11]LL,ZHOU H, HENDRICKS F H J,et al.CroundwaterFlow Inverse Modeling in Non-Multigaussian Media: Per-formance Assessment of the Normal - Score EnsembleKalman Filter[J].Hydrology and Earth System Sciences,2012, 16(2):573-590.
[12]HOSSEINI A H, DEUTSCH C V, MENDOZA C A, et al.Inverse Modeling for Characterization of Uncertainty inTransport Parameters Under Uncertainty of Source Ceometryin Heterogeneous Aquifers[J].Joumal of Hydrology, 2011(3):402-416.
[13]HARBAUCH A W. Modflow-2005, the US Ceological SurveyModular Croundwater Model: the Croundwater Flow Process[R]. Reston, VA: US Ceological Survey, 2005: 1-21.
[14]ZHENC C M, WANC P P.MT3DMS:A Modular Three-Diruensional Multi-Species Transport Model for Simulationof Advection, Dispersion and Chemical Reactions of Con-taminants in Croundwater Systems[ R]. Alabama:AlabamaUniv University, 1999:3-15.
[15]DUAN Q Y, GUPTA V K, SOROOSHIAN S.Suffled Com-plex Evolution Approach for Effective and Efficient ClobalMinimization[J].Journal of Optimization Theory and Ap-plications, 1993, 76(3): 501-521.
[16] SOROOSHIAN S, DUAN Q, CUPTA V K. Calibration ofRainfall - Runoff Models: Application of ClobalOptimization to the Sacramento Soil Moisture AccountingModeI[J]. Water Resources Research, 1993, 29 ( 4) :1185-1194.
[17] RAJ Mohan Singh, BITHIN Datta. Croundwater PoUutionSource Identification and Simultaneous Parameter EstimationUsing Pattem Matching by Artificial Neural Network [ J] . En-vironmental Forensics, 2004, 5( 3) : 143-153.

