基于博弈论和神经网络算法最优路径的设计
李晓启 崔丽琪 宋昱开


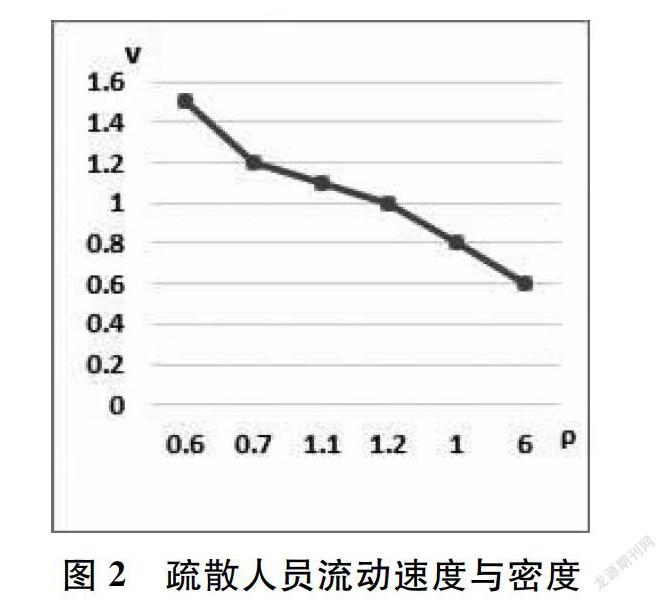

摘要:本文主要研究了旅游景点的应急疏散方案问题。楼层平面内通过博弈论和元胞自动机原理建立了多口人群疏散模型,楼层间通过图论和神经网络算法建立了网络路径优化算法模型。结合这两个模型为景点提供最佳的游客疏散方案。通过层次分析法,将游客疏散分为:在发生紧急情况时游客找到所在楼层的逃生通道和从逃生通道撤离到出口两个过程。在紧急情况发生后,游客会自己选择逃生通道,依据博弈论分析游客权衡出口的宽度和人数、游客距出口的距离,以及出口的阻塞程度等权重后做出选择,当游客去一个通道的收益为最大时,这个出口将成为他首要选择的目标。最终计算出在疏散时选择在就近通道口排队和选择去其他的通道口人数的比例为2:8时,所用时间最短,并使用MATLAB软件对模型进行了仿真分析,计算出使用模型人口疏散的时间比不使用模型一提速了4%,从而证明了模型的合理性。
关键词:人员疏散 敏感性解析 层次分析法 博弈论
1问题重述(略)
2模型假设
1)假设每层的参观者分布均匀;
2)疏散时,人员只向前移动,而不是后退或原地旋转;
3)每层楼的所有入口都变成出口,电梯和自动扶梯停止运行(停止的自动扶梯可用作楼梯),楼梯可以正常使用。
3 模型的建立与求解
人员疏散时对出口的选择过程类似于很多人对有限资源的抢占,人员之间是相互竞争的关系,每个人的目标都是尽快的通过出口。当出口阻塞时该在最近出口附近等待还是应立即更换较远出口问题可通过建立如下模型解决[1]。
但此时模型为逃生者之间的不完全信息的静态博弈,站在策略制定者的角度,利用元胞自动机模型,基于二维离散空间,划分空间分隔为均匀的网格,网格可以由个体占据,也可以由障碍物等占据。每一个个体占據网格上特定的位置,根据更新规则从一个网格位置移动到另一个网格位置[4]。
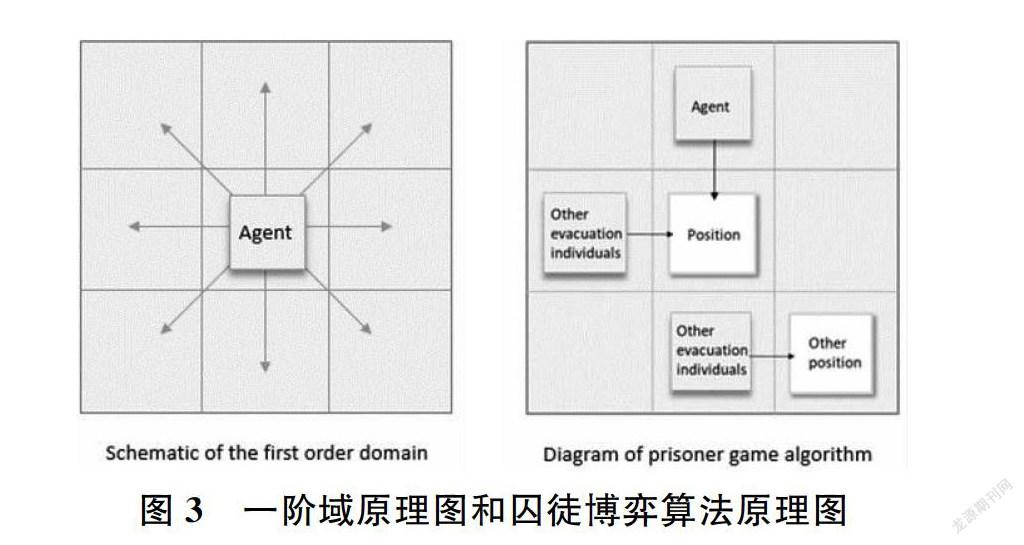
模型时间上采用离散的时间设置,每一个个体向相邻网格移动后按照指定的规则进行更新[5]。综合考虑路径规划、碰撞检测、冲突消解问题,同时参考A-gent模型个体特定属性,反映复杂的人类行为,包括学习其他的逃生策略,疏散路线,适应初始环境所给定的限制等。从空间演化博弈角度,假设所有逃生者的决策是理智,利用元胞自动机的基本框架,智能体模型( Agent- Based Model)来模拟独立存在的个体的行为和个体间的互动,即人群疏散过程中,个体在和其他人员发生冲突时,个体采取竞争策略还是合作策略,就是个体和邻域中其他人员的一个囚徒困境博弈,从而描述逃生者的行为[6]。
在此疏散模型中,位置的同步更新、异步更新、随机更新的结果是一样的。三种顺序的更新都会考虑到周围邻域其他疏散个体博弈收益的影响,此影响是和更新顺序无关的[7],示意图如图3。
参考Swarm仿真结果,模拟复杂的人类行为,提供对环境更加现实的自然描述,预测在出口处人流和疏散时间的关系,即已知静态博弈中其他逃生者策略的情况下,规划每个逃生者根据其他人员对出口的选择时采用的策略,并通过应急人员或指示图标布置实现策略,从而获得最大收益,即以最短时间逃出平面空间,这恰好能很现实的反映紧急状况下人员自身利益最大化的策略选择行为。
最终计算出在疏散时选择在就近通道口排队和选择去其他的通道口人数的比例为:2:8时所用时间最短。
4 模型的检验
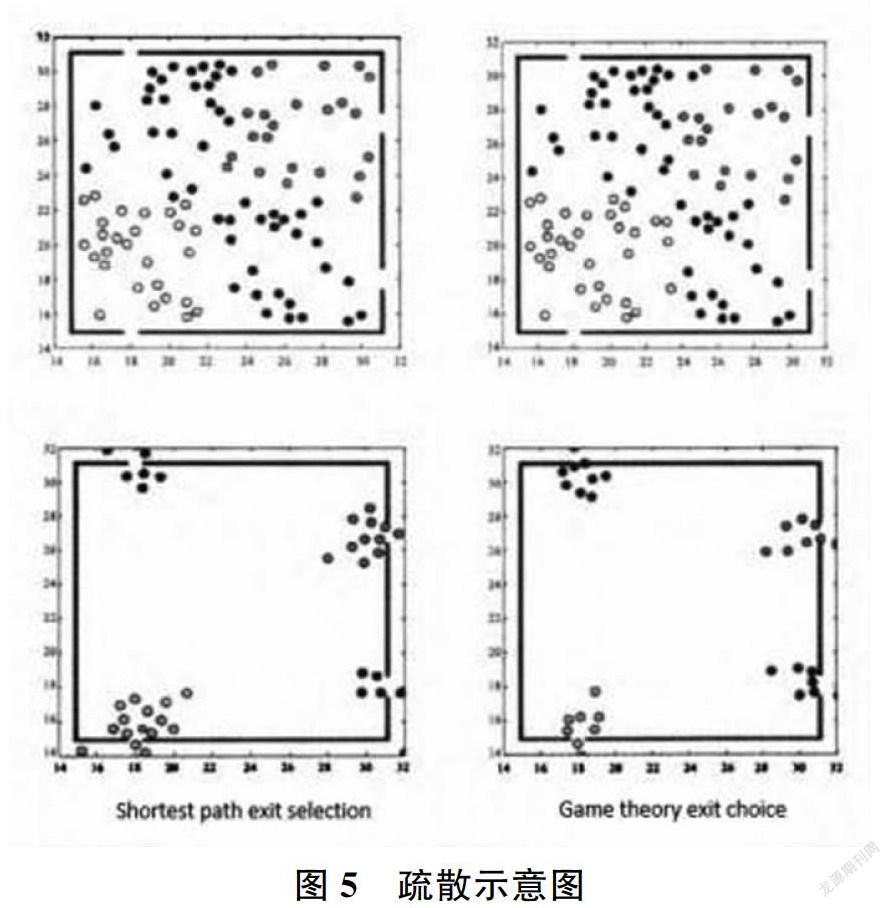
为验证模型的效果,采用MATLAB编程实现了一个多出口房间的疏散仿真,在15m×15m没有任何设施的空房间中初始随机分布100人,房间的4个出口如图5所示分布(上下两个出口宽度为0. 8m,右侧两个出口宽度为1. 2m)。按照指定参数进行疏散。即区域内选择在就近通道口排队和选择去其他的通道口人数的比例为2:8。
由此可得出,使用基于博弈论和元胞自动机的多口人群疏散模型得出的出口安排,比最短路径至少提速4%,如图6所示。
5总结
依据建模结论,针对大型建筑应急疏散,以卢浮宫为例,对于特殊旅客方面:卢浮官2018年的参观游客中,外国游客占比75%,因此卢浮官需要更多的具备这些外语交流能力的工作人员。若结伴旅行的游客(常常指旅行团),始终以团队为单位行动,则可能会造成某撤离必经之路上的拥堵,这样其他的通道不得不为此通道分压,从而使整个疏散系统拥堵的可能性增加,甚至引起群众恐慌,造成更加严重的后果。所以结伴旅行的游客,在疏散时应该遵循应急疏散方案,尽快撤离到安全地区。对于残疾旅客:一般残疾的游客会在家属的陪同下参观,发生紧急情况时,家属会在帮助残疾游客逃离场馆,而也有一些残疾游客会自己参观,在紧急情况时行动缓慢的游客需要在工作人员的协助下完成撤离,因此在除在每个通道口配置一个工作人员,每层楼还需再配备一些备用工作人员用,行动不便的旅客撤离。
针对于是否开启其他出口用于人员的疏散:发生恐怖袭击后,安全人员需要在最短的时间里就位,进行人员的疏散,而游客不会等待安全人员就位后才开始撤离。因此在袭击后安全人员通过正常通道就位难度较大。对于非日常开发的通道,仅有场馆工作人员及官员知道而游客并不知道,同时绝大多数人具有从众心理,在慌乱时不会选择走自己不熟悉的通道。因此这些通道中的容客量会远少于正常通道。我们还可将残疾人员的疏散也安排进这些通道中,从而避免残疾人员在疏散时,对他人或自己造成的不便。综上所述非日常开放的通道中的人员构成是:场馆官员、安全人员、残疾游客、不从众或偶然看到该出口的游客。所以安全人员在疏散人流时不主动提醒非日常开放的通道,当日常开放的通道达到饱和时,再选择性的开放出口以供游客疏散。
参考文献
[1] BRAGLIA M, CASTELLANO D, GABBRIELLIR.基于博弈论的应急出口选择新模型.Advancesin Complex Systems, 2013.
[2]Helivaara S,Kuusinen J M, Rinne T,et a1.通道疏散中行人运动与出口选择的研究[Jl. Safetyseience, 2012, 50(2): 221-227.
[3]Oliveira dos Santos Soares R, Martinez A S.空间囚徒困境中合作演化的几何模式:一种群体内模式[J]。《物理A》:统计力学及其应用,2006,369(2):823-829.
[4]Helbing D.人群自组织理论[M]//社会自组织理论Springer Berlin Heidelberg,2012:71-99.
[5]刘润然,贾春晓,章剑林等,年龄相关的生命力对于囚徒困境博弈合作频率之提升[J].《物理A》:统计力学机器运用,2012,391(18):4325-4330.
[6]Goldengorin B, Krushinsky D, MakarenkoA,大规模人群的同步运动问题//非线性动力学与同步的最新进展Springer Berlin Heidelberg,2009: 227-303
[7]孟园,基于多Agent的大型公共建筑人员应急疏散微观特征分析与仿真研究,2016.6.

