基于确定系数法和信息量模型对新疆特克斯县滑坡敏感性评价的对比研究

张峰 赵忠国 谢大伟 李刚 毛伟

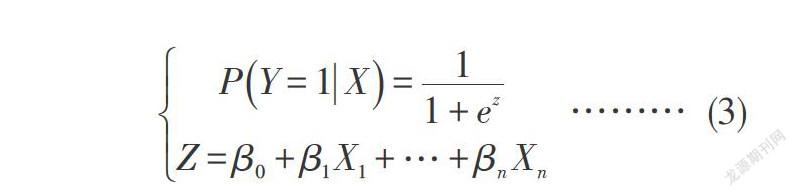
摘  要：在综合当地滑坡灾害发育特征和诱发因素基础上，选取黄土、坡度、坡向、剖面曲率、降雨等12个因子作为滑坡灾害易发性评价因子。利用确定系数法和信息量模型分别与逻辑回归结合构建了LLCF、LLSI两种模型作为滑坡敏感性评价方法。据模型计算结果，将滑坡灾害易发程度划分为极低易发区、低易发区、中易发区、高易发区和极高易发区。利用接收者操作特征曲线（ROC， Receiver Operating Characteristic Curve）及下围面积（AUC，，Area Under the ROC Curve）值分别对两种模型进行精度检验。结果表明：LLCF和LLSI模型在训练集上成功率曲线AUC值分别为0.903 2和0.841 1;在测试集上预测率曲线AUC值分别为0.899 8、0.871 5。整體上LLCF模型精度高于LLSI模型，为当地防灾减灾、国土资源等方面提供了有效的数据支持。

关键词：特克斯县;滑坡敏感性;确定系数法;信息向量模型;逻辑回归

随着气候变化及城镇化、人类活动等因素影响，滑坡等地质灾害变的非常活跃，我们需重视对地质灾害的易损性评价及区划❶。滑坡敏感性评价是以地质环境条件为基础，综合分析地质灾害发生的控制条件及诱发条件，预测地质灾害在一定区域内发生的可能性[1-2]。目前对滑坡敏感性评价主要采取定性和定量方法评估[3-5]。定性方法快捷简单，可实现对地质灾害易发性的快速分析判断和评价，其局限性是对参与模型因子权重的确定存在主观性，同时模型的应用性也受地域限制，缺乏可重复性[6-7]。定量物理模型和数学模型具不同的局限性，如物理模型准确性受单个斜坡或研究区岩土参数影响较大，仅适合小范围或单个灾害评估等[8-9]。数学模型需大量精度高的地质水文数据，因此数据选择和要素等级划分差异对输出结果影响较大[10]。近年来，3S技术的快速发展有效提高了区域地质灾害敏感性评价模型的评价精度，尤其是基于GIS的不同模型方法组合使用在地质灾害敏感性评价中得到广泛应用并取得良好效果。

1  研究区概况

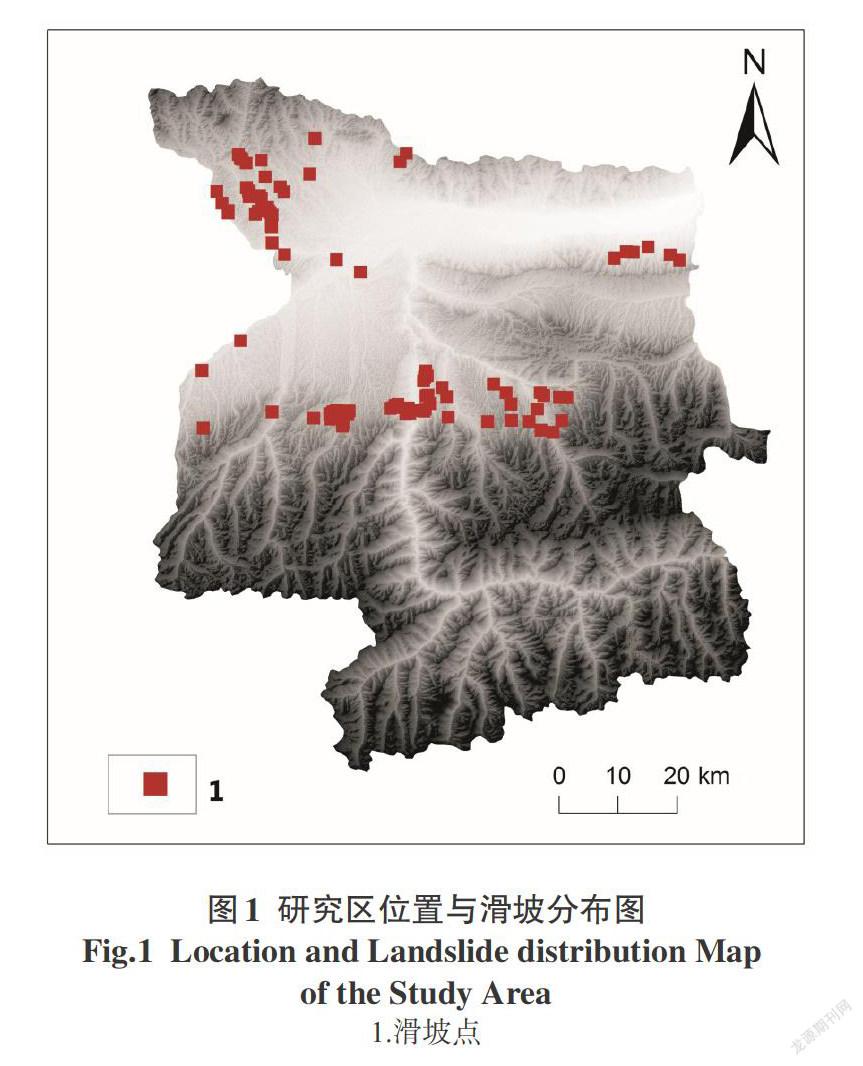
特克斯县位于新疆维吾尔自治区北纬42°22′30″～43°25′30″，东经81°19′00″～82°37′30″。特克斯县属山区县，面积8 352 km2，93%的面积为丘陵地，研究区海拔919～4 958 m，地势呈北低南高（图1）。该区气候为典型北温带大陆性气候，年平均气温约5.3 ℃，年降水量约382.3 mm，日照2 719 h，主要地质灾害为滑坡、泥石流、崩塌等。

2  数据来源与研究方法

2.1  数据来源

本文在实地调查和收集现有资料基础上，分析当地地质环境、地质灾害分布规律、发育特征及形成条件，选取了数字高程模型、距断层距离、岩性、起伏度、土壤类型、平面曲率、黄土分布、年降水量和归一化植被指数，在数字高程模型（DEM）基础上，分别提取坡向、坡度、剖面曲率为滑坡易发性评价因子。以上参与滑坡条件因子均通过ArcGIS等相关软件处理。据91个实测监测滑坡数据点随机按7∶3比例划分为两个子集，标记为“1”（图1）。另在非滑坡区域随机生成91个相同数量的非滑坡点，同样按7∶3比例划分为两部分，标记为“0”。最后得到128个训练模型数据和54个验证数据。

2.2  研究方法

2.2.1  确定系数法（CF）

[Pa]为事件（地质灾害）在因子分类数据a中发生的条件概率，实际研究中通常用因子分类a中的地质灾害个数（或面积）与数据分类a的面积比值表示。[Ps]为整个研究区灾害总个数（或面积）与研究区总面积比值。CF变化区间为[-1，1]，当CF值为正时，其值越大，表明该单元为滑坡易发区;当CF值为负时，其值越小，表明该区域不易发生滑坡[11] 。

2.2.2  信息量模型 （SI）

信息量模型认为可根据评价因子推算出信息值预测是否发生滑坡的概率。当信息量值为负时，数值越小，表明滑坡易发性的可能性较低。信息量值越大，表明滑坡易发性的可能性较高[12]。

[I=i=1nIxi，H=i=1nlnNiNSiS]…（2）

式中，[xi]代表评价单元内所取的因子等级，[Ixi，H]为因子[xi]对地质灾害贡献的信息量;[S]为研究区面积;[S]为研究区内含有因子[xi]的面积;[N]为研究区地质灾害总数;[N]为发生地质灾害区域内含有因子[xi]的数量，[I]为评价单元中综合信息量;n 为影响因子数量。

2.2.3  逻辑回归

逻辑回归是研究分类结果与影响因子之间的一种常用的多元统计分析方法。滑坡灾害建模分析中，它被描述为二元因变量（一般来说，1表示滑坡，0表示非滑坡）与其他自变量（X1，X2，...，Xn）之间的关系[11]。

[PY=1X=11+ezZ=β0+β1X1+…+βnXn]…（3）

其中[P]为滑坡灾害发生的概率，取值范围为[0，1] ，[β]为逻辑回归系数。

3  结果分析

3.1  多重共线性分析

滑坡敏感性评价中，由于所选因子在参与回归分析中可能存在多重共线性问题，因此会降低构建模型的预测准确性。本文在R语言中实现lasso的运算，分析因子之间的多元共线性问题。通过训练集和验证集分别得到各因子对应的Lasso系数，达到滑坡敏感性因子的筛选。最终选取高程、土壤类型、年均降雨量、坡度、起伏度、黄土、岩性参与滑坡敏感性模型构建分析（表1）。

3.2  滑坡因子与滑坡分布相关性分析

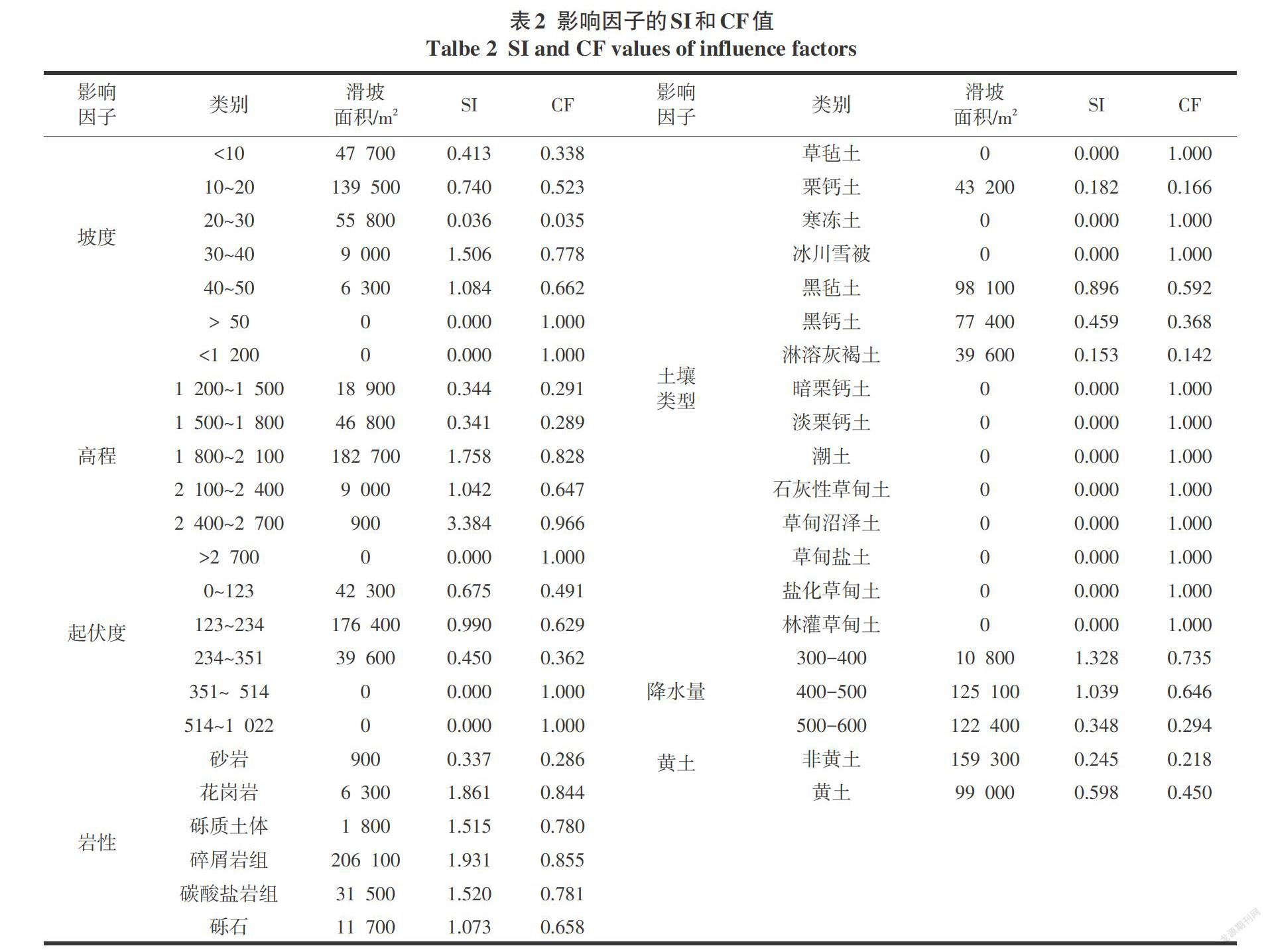
滑坡敏感性分区精度取决于所选的影响因子，深入理解每个影响因子与滑坡灾害点的关系有助于提高滑坡敏感性评价及分区效果。通过将高程、土壤类型、年均降雨量、坡度、起伏度、黄土、岩性因子按公式（1）和（2）分别计算上述因子在不同分级中的SI和CF的值，表明滑坡易发性趋势（表2）。

坡度影响因子中，10°～20°内滑坡分布比为54.01%。高程因子中，1 800～2 100 m滑坡分布比为70.73%。降水因子中，降水量在400～500 m中滑坡分布比为48.43%。起伏度方面 ，滑坡面积68.29%分布在123～234范围。岩性方面，碎屑岩组滑坡分布比为79.79%，其他岩性分组占比较少。我们按全国1∶100土壤分类图，将研究区土壤划分为15类，其中黑毡土发生滑坡占比为37.98%，黑钙土滑坡分布占比为29.97%，两类共占滑坡总面积比的67.95%。

3.3  滑坡敏感性评价结果

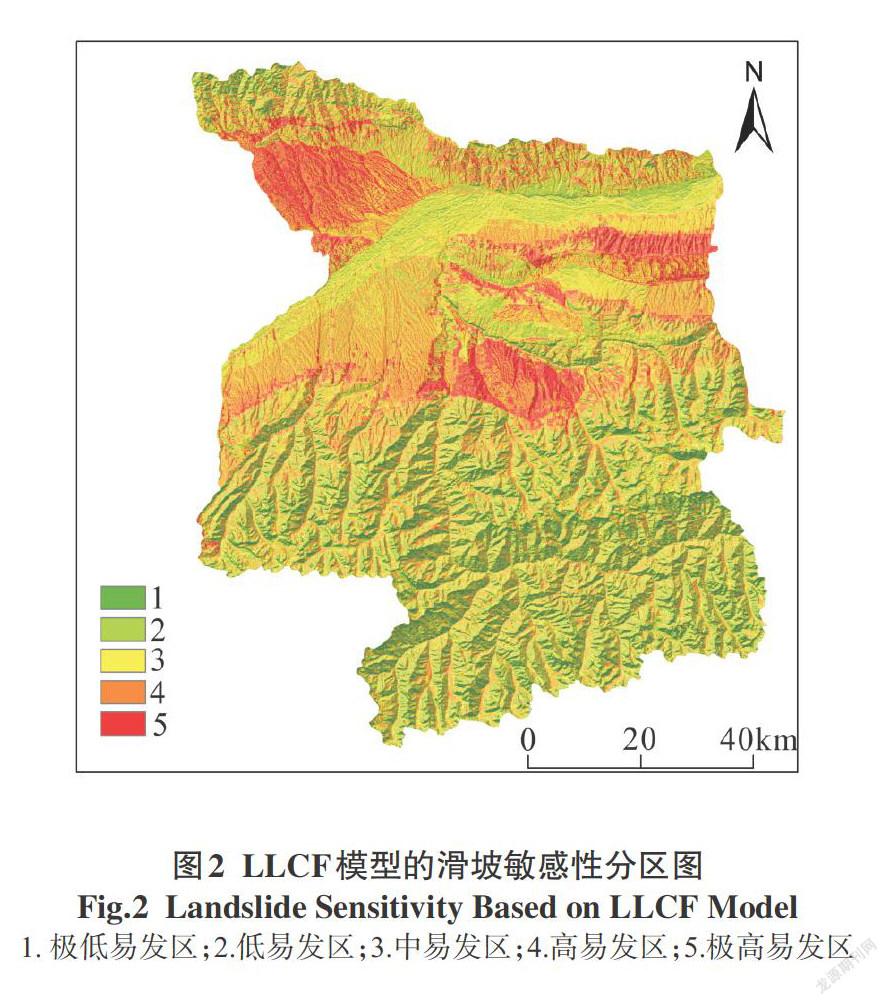
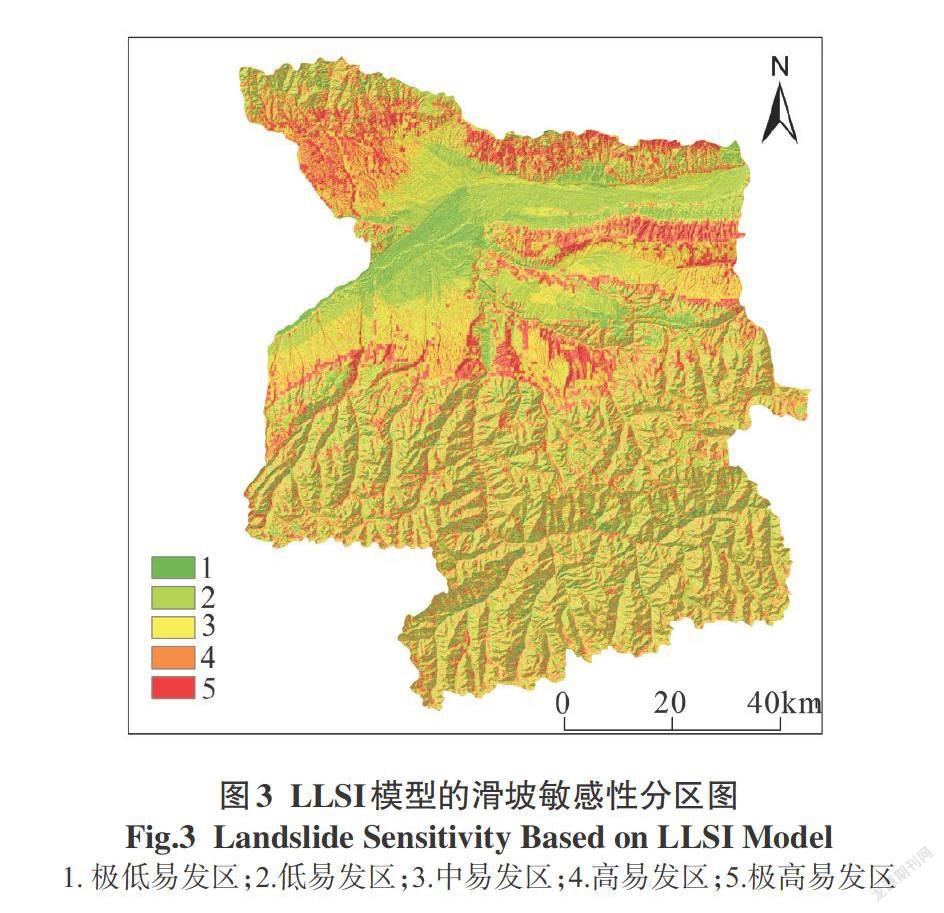
本文将滑坡灾害点样本的高程、坡度、土壤类型、年均降雨量、起伏度、黄土、岩性信息量模型的值（SI）和确定系数法的值（CF）参与到逻輯回归模型分析中，将评价因子分类级别的SI值和CF值作为自变量，是否发生地质灾害作为因变量（1代表地质灾害样本点，0代表非地质灾害样本点），在SPSS软件中计算逻辑的回归系数，并构建LLSI和LLCF模型，得到滑坡敏感性分区图（图2，3）。本文将滑坡敏感性按照自然间断点法划分为5类（极低易发区、低易发区、中易发区、高易发区、极高易发区）。其中通过LLSI模型划分得到的极低易发区面积（12.33%）、低易发区面积（25.07%）、中易发区面积（28.76%）、高易发区面积（23.46%）和极高易发区面积（10.38%）;通过LLCF模型划分得到的极低易发区面积（11.53%）、低易发区面积（23.56%）、中易发区面积（30.06%）、高易发区面积（25.71%）和极高易发区面积（9.14%）。

3.3  评价模型精度验证

为进一步验证滑坡敏感性分区意义，利用训练集数据和测试集数据，分别对LLCF、LLSI两种模型进行精度检验。

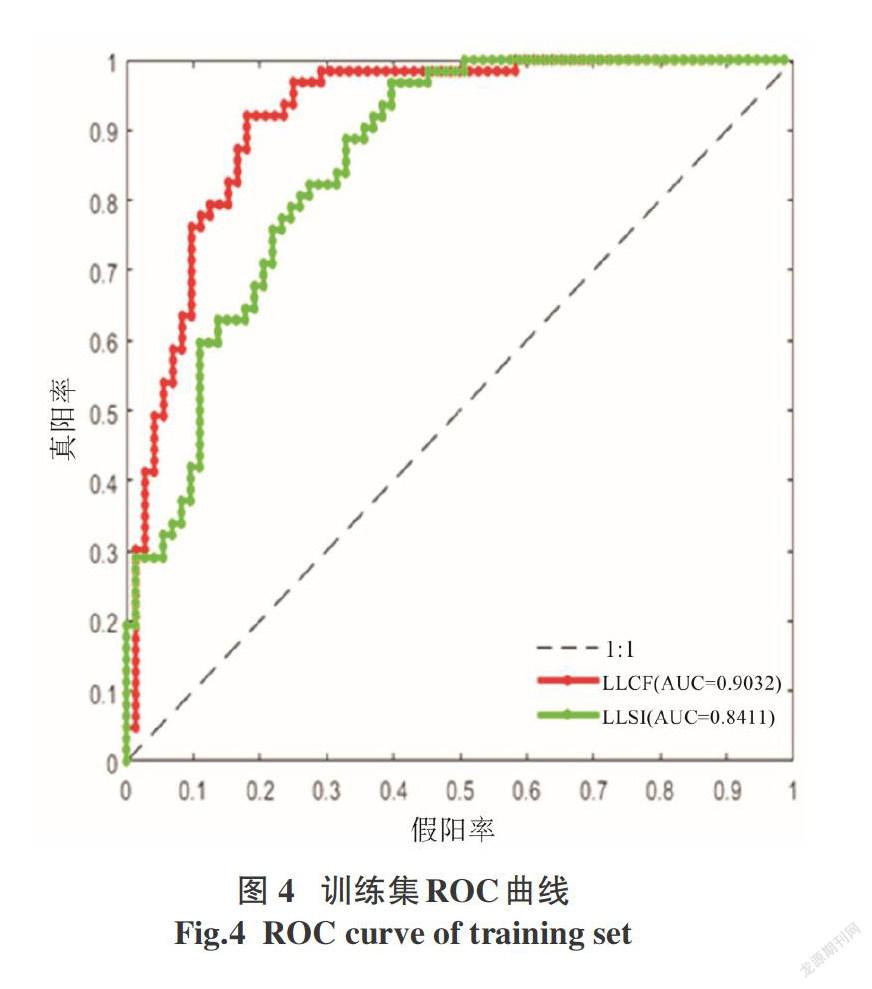
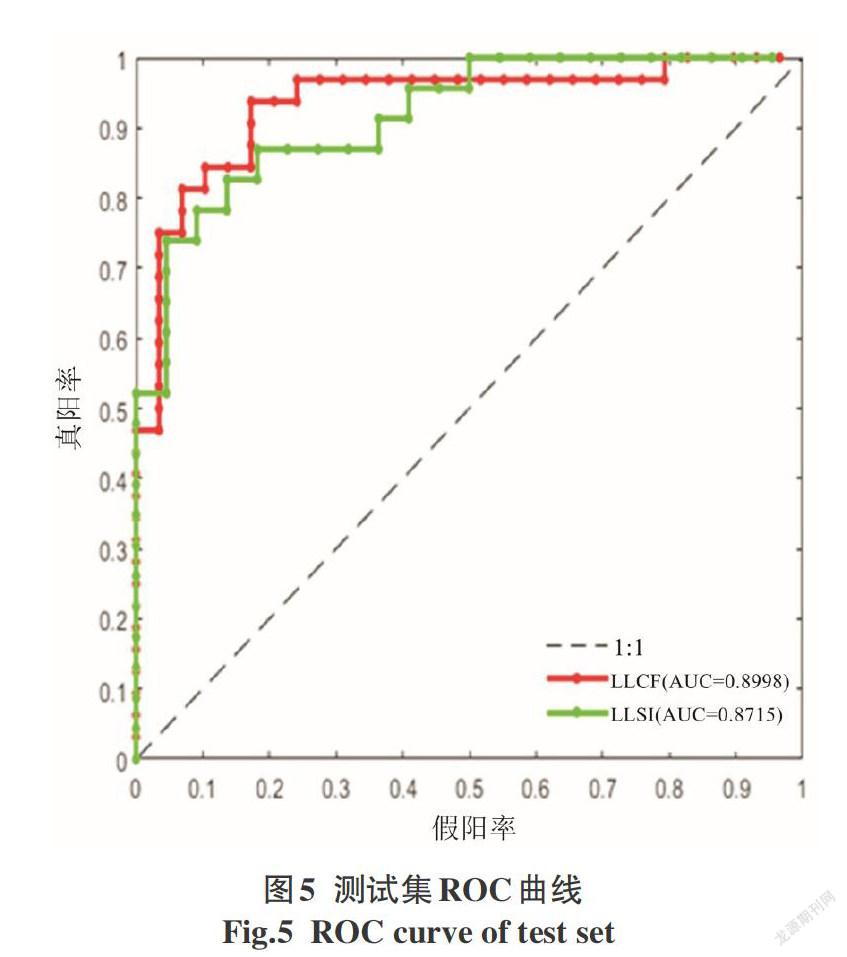
接收者操作特征曲线（ROC）是评价滑坡敏感性模型的有效方法，但往往ROC曲线不能清晰表明哪个模型的效果更佳，因此我们结合ROC曲线下的面积（AUC）值评价模型。AUC值一般为0.5～1，模型AUC值越大，对应模型效果越好[12]。利用模型建立过程中使用的滑坡数据集和模型建立过程中未使用的滑坡数据集，对两个模型得出的滑坡敏感性进行测试。本文通过接收者操作特征曲线（ROC）和ROC曲线下方的面积大小（AUC）对模型拟合优度及预测能力进行评价。X轴为错误分类的非滑坡位置，Y轴为成功分类的滑坡位置，ROC曲线下面积越大，模型的性能越好。LLCF和LLSI模型在训练集上的AUC值分别为0.903 2和0.841 1（图4）。LLCF和LLSI模型在测试集上的AUC值分别为0.899 8和0.871 5（图5）。整体上LLCF模型精度高于LLSI模型，从模型精度评价可知，基于LLCF模型的滑坡敏感性评价效果高于LLSI模型，高敏感性等级区间基本覆盖了已有实测滑坡监测点，从一定程度上说明基于LLCF模型的滑坡敏感性评价方法可行。

4  结论

本文以新疆特克斯县地质灾害详查的91个地质灾害点为基础，选取高程、距断层距离、坡度、坡向、剖面曲率、起伏度、土壤类型、黄土分布、年降水量、平面曲率，岩性和归一化植被指数作为地质灾害敏感性评价因子。分别采用确定系数法（CF）和信息量法（SI）与逻辑回归结合构建LLCF和LLSI模型，通过ROC曲线下面积AUC值分别对LLCF、LLSI模型进行精度检验，整体上基于LLCF模型精度优于LLSI模型。因此，LLCF模型对本研究区地质灾害敏感性分区方法具有适用性。

参考文献

[1]    Cruden DM .A simple definition of a landslide[J].Bulletin of Engineering Geology and the Environment，1991，43 （1）： 27-29.

[2]   Guzzetti  F， Reichenbach P， Cardinali M， et al. Probabilistic landslide hazard assessment at the basin scale[J]，2005，72（1/2/3/4）：272 -299.

[3]    Guzzetti F， Carrara A， Cardinali M， et al. Landslide hazard evaluation： a review of current techniques and their application in a multi-scale study， central Italy[J]. Geomorphology，1999，31（1-4）：181-216.

[4]    Ayalew L， Yamagishi H..The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains，Central Japan[J]. Geomorphology， 2005，65（1-2）：15-31.

[5]    Corominas J， van Westen C， Frattini， P， et al. Recommendations for the qunantiative analysis of landslide risk[J]. Bulletin of Engineering Geology and the Environment. 2014， 73（2）：209-263.

[6]    Saha AK，  Gupta RP ， Sarkar I，et al.An approach for GIS-based statistical landslide susceptibility zonation—with a case study in the Himalayas[J]. Landslides， 2005，2（1）： 61-69.

[7]    Kanungo， DP， Arora， Mk， Gupta， RP， et al. A comparative study of conventional， ANN black box， fuzzy and combined neural and fuzzy weighting procedures for landslide susceptibility zonation in Darjeeling Himalayas[J].Engineering Geology. 2006. 85（3-4）： 347-366.

[8]    Aleotti P， Chowdhury R .Landslide hazard assessment： summary review and new perspectives[J]. Bulletin of Engineering Geology and the Environment ， 1999，58（1）：21-44.

[9]    Baeza C， Corominas J. Assessment of shallow landslide susceptibility by means of ultivariate statistical techniques[J]. Earth Surface Processes and Landforms， 2001，26（12）： 1251-1263.

[10]  Mousavi SZ， Kavian A， Soleimani K，et al. GIS-basedspatial prediction of landslide susceptibility using logistic regression model[J]. Geomatics， Natural Hazards and Risk， 2011，2 （1）， 33-50.

[11]  田春山，劉希林，汪佳. 基于 CF 和 Logistic 回归模型的广东省地质灾害易发性评价[J]. 水文地质工程地质，2016，43（6）：154-170.

[12]  张晓东，刘湘南，赵志鹏. 信息量模型、确定性系数模型与逻辑回归模型组合评价地质灾害敏感性的对比研究[J].现代地质，2018，32（3）：602-610.

Comparative Study on Landslide Sensitivity Assessment in Turks County of Xinjiang Based on Determined Coefficient Method

and Information Quantity Model

Zhang feng1， Zhao Zhongguo2，Xie Dawei1，Li Gang1，Mao wei1

（（1.Xinjiang Vocational and Technology college of communication， Urumqi，Xinjiang，830000，China;2.Xinjiang University，Urumqi，Xinjiang，830000，China）

Abstract：On the basis of synthetically considering the development characteristics and inducing factors of local landslide hazards，twelve factors，such as loess，slope gradient，slope direction， section curvature and rainfall，were selected to evaluate the susceptibility of landslide hazards. LLCF and LLSI models are constructed by combining deterministic coefficient method and information model with logistic regression respectively.According to the calculation results of the model， the vulnerability of landslide disasters can be divided into extremely low-vulnerable areas， low-vulnerable areas，medium-vulnerable areas，high-vulnerable areas and extremely high-vulnerable areas.The accuracy of the two models is tested by using ROC （Receiver Operating Characteristic Curve） and AUC （Area Under the ROC Curve） values. The results show that the AUC values of LLCF and LLSI models on the training set are 0.903 2 and 0.841 1 respectively， and the AUC values of predictive rate curve on the test set are 0.899 8 and 0.871 5 respectively. Overall，the accuracy of LLCF model is higher than that of LLSI model，which provides effective data support for local governments in disaster prevention and reduction，land and resources，etc.

Key words：Turks County;Landslide Sensitivity;Determined Coefficient Method;Information Vector Model;Logical Regression