反铁磁性铜配合物密度泛函理论研究

尹乾柱 崔术新 沈金铭 赵一伦

摘 要：应用密度泛函理论结合破损态方法对铜配合物（bmim）2[Cu3（μ3-OH）（μ-Cl）（μ-pz）3Cl3]（bmim+=1-丁基-3甲基咪唑阳离子，pz-=吡唑阴离子）磁性质进行理论研究.通过八种密度泛函方法（B3P86，B3LYP，PBE，PBE0，B3PW91，BP86，BLYP，M06）在五种基组（LANL2DZ，6-31G-SVP，TZVP-SVP，6-31G，SDD）水平下对该配合物磁耦合常数计算的结果表明，实验数据与实验值符号一致，其中在BP86//6-31G-SVP水平上所得的耦合常数值为-99.61 cm-1，与实验数值（-98 cm-1）符合程度最为接近，说明单占据轨道间的能量劈裂是配合物表现反铁磁性耦合的原因.

关键词：铜配合物;反铁磁性;密度泛函理论;对称性破损态

[中图分类号]O 646.8    [文献标志码]A

Theoretical Studies on the Antiferromagnetism Copper Complex

YIN Qianzhu，CUI Shuxin*，SHEN Jinming，ZHAO Yilun

（College of Chemistry and Chenical Engineering， Mu Danjiang NormalUniversity， Mudanjiang 157011， China）

Abstract：The magnetic properties of complex such as （bmim）2[Cu3（μ3-OH）（μ-Cl）（μ-pz）3Cl3]（bmim+ = 1-butyl 3-methylimidazole， cationic， pz- = pyrazole anion） were studied using broken symmetry （BS） approach combined with density functional theory （DFT）. The magnetic coupling constants of the complex were calculated at five basic sets （LANL2DZ， 6-31G-SVP， TZVP-SVP， SDD， 6-31G） by eight density functional methods （B3P86， B3LYP， PBE， PBE0， B3PW91， BP86， BLYP， M06）. The calculation results show that the data obtained are consistent with the experimental values. Among them， the coupling constant of the complex was calculated to be -99.61 cm-1 at the level of BP86//6-31G-SVP， which is the closest to the experimental value （-98 cm-1）. This shows that the energy splitting between the occupied orbits is the cause of the antiferromagnetic coupling of the complex.

Key words：copper complex; antiferromagnetism; density functional theory; symmetry broken state

金屬配合物作为一种新型功能性分子材料，不仅具有丰富的空间拓扑结构，而且呈现出独特的光、电、磁、催化、吸附等性质，在客体交换与分离、手性拆分、药物缓释、电致发光、磁性固体等方面均显示出潜在的应用前景.[1]配合物磁性研究非常广泛，寻找性质与结构之间的关系，从理论上设计与筛选出具有预期性质的目标分子，引起众多研究者的关注.本文设计了一类由常见配体为桥连配体的配合物，探讨桥连配体对配合物磁性质的影响，确定配合物结构与性质间的相关性，并探讨以席夫碱、乙酸为配体的配合物磁结构相关性.[2]本文选择Athabassions等合成以常见配体羟基及卤素氯为桥连配体形成的铜配合物（bmim）2[Cu3（μ3-OH）（μ-Cl）（μ-pz）3Cl3]为研究对象[3]，采用密度泛函理论结合对称性破损态（DFT-BS）研究分子磁交换反应机理[4]，对金属离子配合物交换耦合常数进行理论模拟计算;选用不同的基组和方法来探究配合物的磁性结构相关性关系，为认识新合成配合物及其性质和结构之间的关系提供理论依据.

1 计算部分

1.1 计算模型

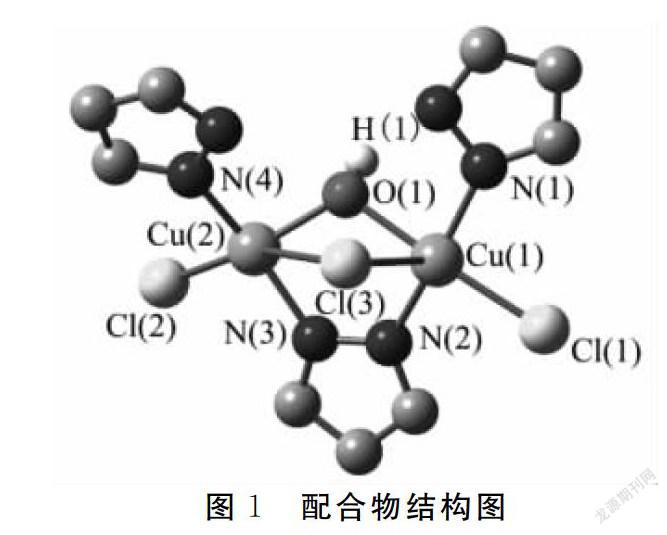
模型中所有分子的原子坐标直接来自于实验的晶体结构数据，其原始数据并未进行任何改变.因三核铜配合物（bmim）2[Cu3（μ3-OH）（μ-Cl）（μ-pz）3Cl3]不是对称体系，三核体系可以裁切成三个双核铜配合物体系，但三个体系结构相似，仅中心离子Cu2+之间的距离不同.bmim+未对磁性产生贡献.笔者将含有较近的两个金属离子距离的体系作为此次的计算模型，其结构如图1所示.

1.2 计算方法

为了探究方法和基组对磁耦合常数J准确度的影响，选用几种密度泛函方法：广义梯度近似（General Gradient Approximation GGA）（BLYP，BP86，PBE）、杂化密度泛函（Hybrid Density Functional Theory HDFT）（B3LYP，B3PW91，PBE0，B3P86）和超密度梯度近似（meta-GGA）（M06）;选用不同基组（LANL2DZ，6-31G-SVP，TZVP-SVP，6-31G，SDD）进行计算.对于两种混合基组（6-31G-SVP，TZVP-SVP），Cu原子采用的是6-31G基组，其他原子（C，H，O，N）采用的是SVP基组;对于混合基组TZVP-SVP，Cu原子采取的是TZVP基组，其他原子（C，H，O，N）采用的是SVP基组.由Gaussian 09计算软件完成所有计算工作.

2 结果与讨论

2.1 磁耦合常数J

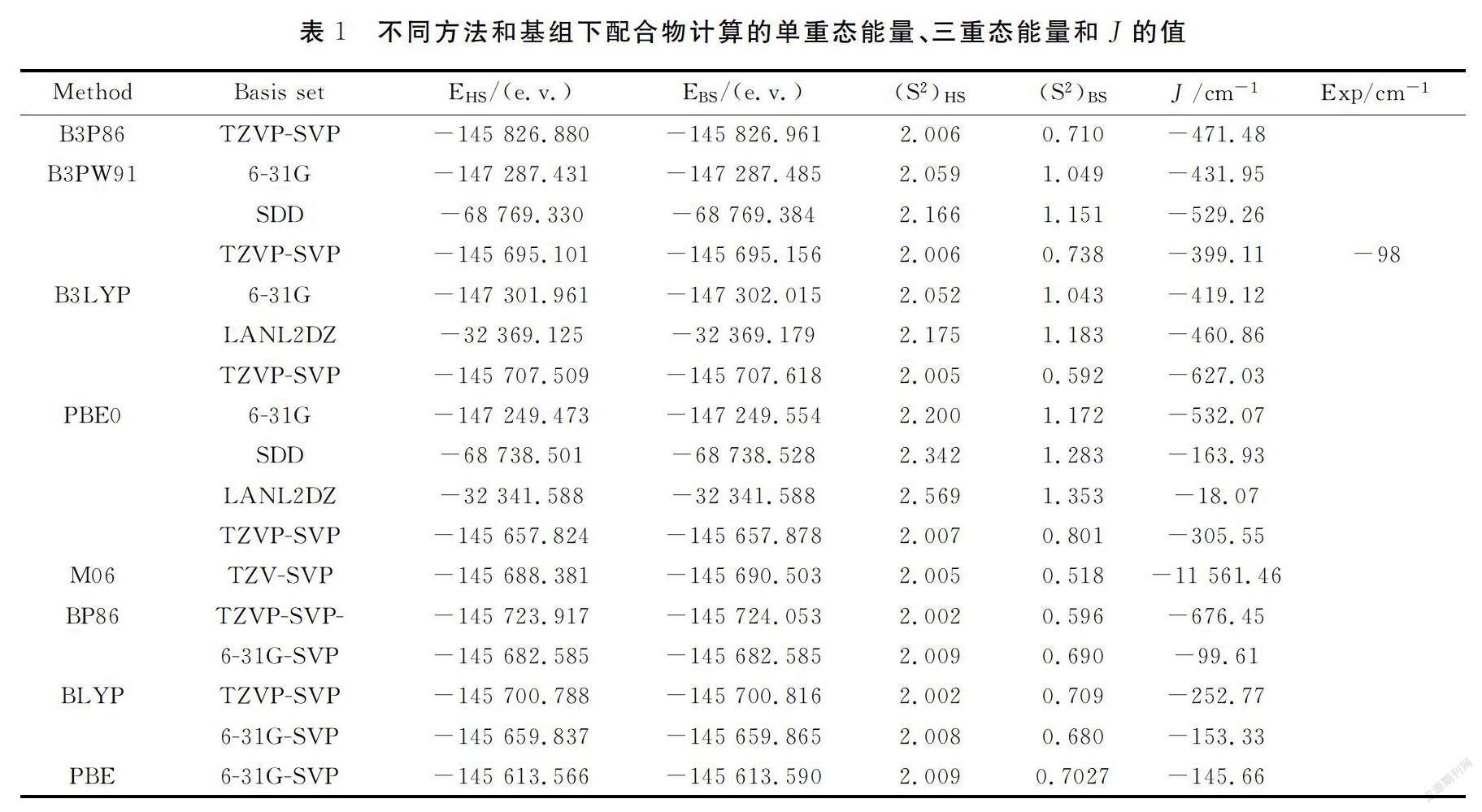
磁耦合常数在讨论磁性时有着非常重要的意义，为了体现磁耦合常数的基组和方法效应，采用多种方法在不同的基组水平下计算配合物的磁耦合常数J（表1），计算值与实验值的符号一致.单一基组LANL2DZ水平下不同方法（PBE0，B3LYP）所得磁耦合常数大小顺序为：B3LYP>PBE0.单一基组6-31G水平下不同方法（B3PW91，B3LYP，PBE0）所得磁耦合常数大小顺序为：PBE0>B3PW91>B3LYP.单一基组SDD水平下不同方法（PBE0，B3PW91）所得磁耦合常数大小顺序为：B3PW91>PBE0;混合基组6-31G-SVP水平下不同方法（BP86，BLYP，PBE）所得磁耦合常数大小顺序为：BLYP>PBE>BP86.混合基组TZVP-SVP水平下不同方法（B3P86，B3PW91，BP86，BLYP，B3LYP，PBE0，M06）所得磁耦合常数大小顺序为：M06>BP86>B3LYP>B3P86>B3PW91>PBE0>BLYP.采用混合基组的所得磁耦合常数较单一基组更接近实验值.在相同方法水平下（BP86）不同基组（TZVP-SVP，6-31G-SVP）所得磁耦合常数大小顺序为： TZVP-SVP >6-31G-SVP（表2），由此可见，磁耦合常数对方法没有依赖性，对基组有一定的依赖性.计算结果表明，GGA泛函较其他泛函适用，3种GGA方法在混合基组6-31G-SVP水平得到耦合常数与实验值更接近，因为磁性主要来源于金属，也就是开壳层的计算即单电子的计算，因此，对于金属Cu原子采用一个相对较大的加入弥散函数的6-31G基组，而对其他配体原子采用相对较小的基组SVP，这种方法和基组的结合对于这个体系可能更具有优势.采用BP86//6-31G-SVP水平下得到磁耦合常数数据为J=-99.61cm-1，与理论值（-98 cm-1）最吻合.

2.2 分子磁性軌道

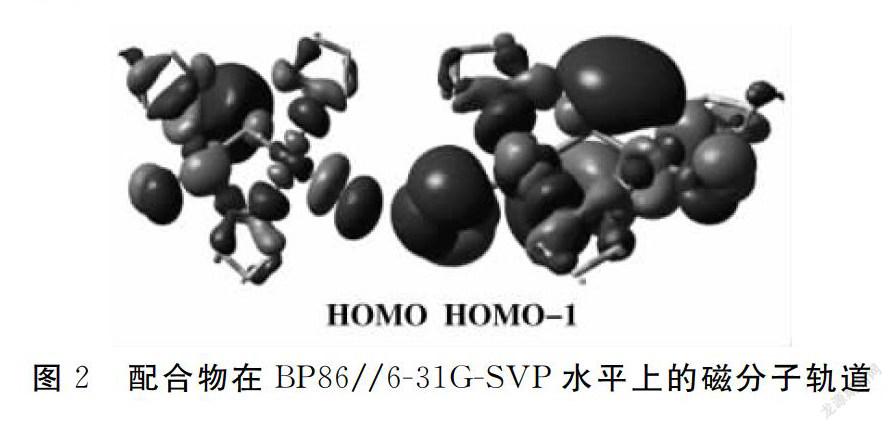
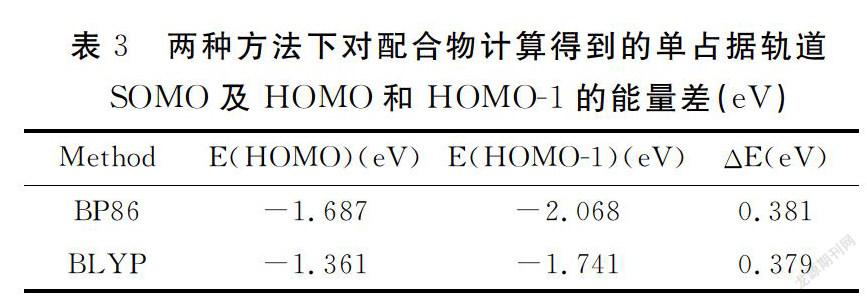
根据Hoffmann理论，定性分析分子磁性轨道来探究磁轨道和配合物性质之间的关系.单占据轨道SOMOS的分布方式表明，配合物中对磁性起重要作用的部分是两个铜原子的d轨道，吡唑环上的N-N桥和Cl桥也对磁性有贡献（图2）.选用三重态计算所得的占据轨道能量值和单占据轨道间的劈裂值ΔE数据进行研究，结果见表3.计算结果ΔE（0.379～0.381 eV）几乎相等，单占据轨道间的能量劈裂是配合物表现反铁磁性耦合的原因.

2.3 自旋密度分析

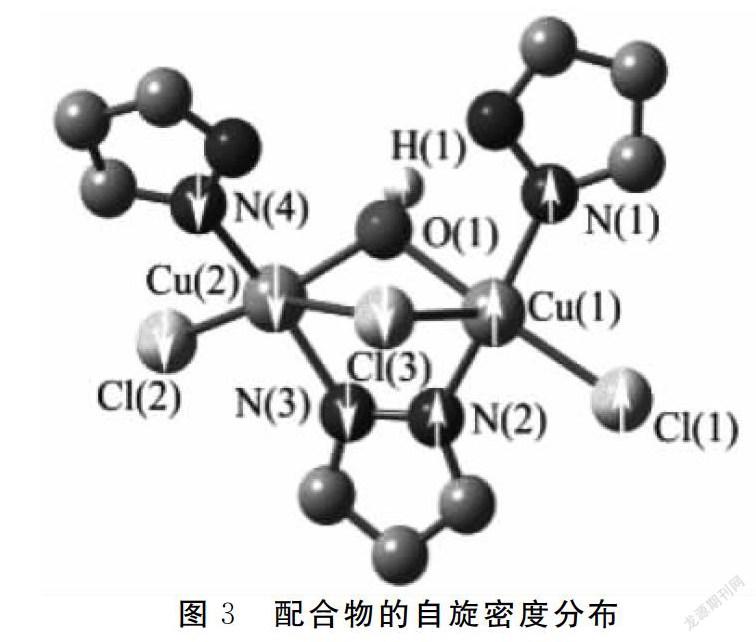
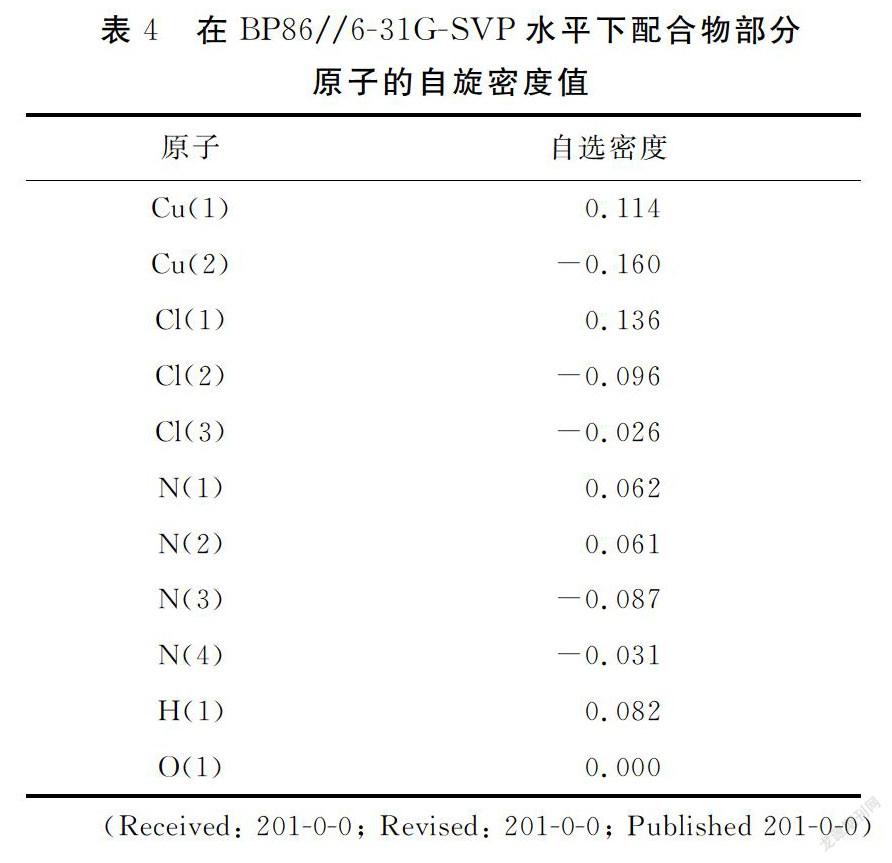
在BP86//6-31G-SVP水平下进行自旋密度分析，结果见图3和表4.金属中心Cu（1）的自旋值为0.114，而Cu（2）的自旋值为-0.160，与Cu（1）配位的非桥连原子（N（1），N（2）和Cl（1））自旋密度值均为正，与Cu（2）配位的非桥连原子（N（3），N（4）和Cl（2））自旋密度值为均负值，说明配合物中金属中心和与其连接的配体存在自旋离域效应.值得一提的是，桥连原子OH-（H（1））与Cu（1）自旋密度值符号相同，与Cu（2）符号相反，而桥连原子Cl（3）与自旋密度值符号相同，与Cu（1）符号相反，表明金属中心与配体原子之间还存在自旋极化效应.结合图3和表4可看出，配合物存在三条磁通道，分别为 （Cu（1）-O（1）H（1）-Cu（2）），（Cu（1）-N（2）-N（3）-Cu（2）），（Cu（1）-Cl（1）-Cl（3）），这三条磁通道对配合物的磁耦合作用有贡献.

2.4 结论

采用不同DFT方法和不同的基组对铜配合物进行理论计算，计算结果显示出八种密度泛函方法计算所得数据的符号与实验值符号一致，且采用混合基组所得耦合常数较单一基组更接近实验值.计算数据还表明，方法和基组的选择对配合物磁耦合常数的准确度有影响，采用BP86方法在混合基组6-31G-SVP基组水平下得到耦合常数数据为J=-99.61 cm-1，与实验值最接近.分析Cu配合物体系的单占据轨道SOMOS的分布方式，能量劈裂及Mulliken布局，研究其配合物的磁交换机制，发现在配合物中存在自旋离域和自旋极化效应，单占据轨道间的能量劈裂是配合物表现反铁磁性耦合的原因.

参考文献

[1]Kozlenko D P， Belozerova N M， Ata-Allah S S，et al. Neutron diffraction study of the pressure and temperature dependence of the crystal and magnetic structures of Zn 0.3 Cu 0.7 Fe 1.5 Ga 0.5 O 4， polycrystalline ferrite[J]. Journal of Magnetism and Magnetic Materials， 2018， 449：44-48.

[2]沈金铭，尹乾柱，包双，崔术新.氰酸桥联双核镍配合物的磁性理论研究[J].分子科学学报，2019，35（3）：238-241.

[3]Boudalis A， Rogez G， Heinrich B， et al. Towards ionic liquids with tailored magnetic properties： bmim+ salts of ferro- and antiferromagnetic CuII3 triangles[J]. Dalton Trans， 2017， 46：12263-12273.

[4]邓琼，刘慧君，丁娟，等.咪唑型离子液体催化Diels-Alder反应的理论研究[J].南华大学学报：自然科学版，2007（1）：49-52+58.

编辑：琳莉