基于演化博弈模型的股价动量效应和反转效应分析

宋光辉　陈苗臻　许林

【摘要】将前景理论与交易成本理论纳入演化博弈理论框架，构建演化博弈模型研究股价动量效应与反转效应的形成机理、均衡的动态调整过程及其影响因素。模型求解结果表明，前景理论的锚定效应是动量与反转效应形成的根源。有限理性的投资者通过重复博弈试错，逐渐形成一致性交易策略，使股价呈趋势性变化，产生动量效应，一定时间后这种一致性交易策略将逆转，產生反转效应。进一步仿真分析发现，交易成本、投资者人数会对动量和反转效应产生显著影响。

【关键词】动量效应;反转效应;形成机理;演化博弈;仿真分析

【中图分类号】F832.5

【文献标识码】A【文章编号】1004-0994（2019）09-0156-8

传统金融学的有效市场假说认为，股票市场中的全部信息都已经反映在股票价格中，故任何投资者都不可能在市场中获得超额收益[1]，然而大量的实证结果表明股票价格存在“动量效应[2]”和“反转效应[3]”。动量效应是指股票价格在未来一段时期的变化趋势将延续过去的趋势，即过去表现良好（上涨）的股票未来仍将继续表现良好，而表现较差（下跌）的股票未来仍将表现较差;反转效应是指过去表现良好的股票将在未来表现较差，而过去表现较差的股票将在未来表现良好。

一、文献综述

显然，有效市场理论无法解释动量效应与反转效应这两种市场“异象”。因此，学者们尝试从行为金融学的角度解释动量与反转效应的成因，主要形成了四类最具代表性的理论。其中，Barberis等[4]的BSV模型和Barberis等[5]的BHS的模型都假设投资者是事前相同的，区别在于：前者认为投资者存在代表性偏差与保守性偏差，这两种偏差分别导致了投资者对股价存在反应不足和反应过度，并最终产生动量与反转效应;后者则从投资者对风险的厌恶程度入手，将动量与反转效应的成因归于前景理论[6]中的“锚定效应”。Daniel等[7]的DHS模型以及Hong、Stein[8]的HS模型则假设市场中存在不同类型的投资者，区别在于：前者认为市场中存在知情者和不知情者，知情者会根据私人信息做出决策，过度自信与自我归因的心理导致了股价动量效应，不知情者则根据公开信息做出决策，并当公开信息确定时导致股价反转;后者认为市场中存在信息观察者与动量交易者，前期由于私人信息的传播需要时间，信息交易者对私人信息反应不足，而动量交易者基于过去价格的走势进行决策，导致股价产生动量效应，后期随着信息在市场中完全扩散，股价则重新回落到均衡水平，产生反转效应。

国内学者尝试对上述四种理论进行修正，以期得到与我国证券市场更吻合的模型。鲁臻、邹恒甫[9]将政府的政策信息引入HS模型，得出由于我国股市具有政策市的特征，反转效应比动量效应更加明显的结论。张荣武、赵行亮[10]将经济周期因素纳入BHS模型，更好地解释了股权溢价之谜等市场异象。谭小芬、林雨菲[11]应用BSV模型解释我国股市投资者多关注短期趋势，喜好“追涨杀跌”，具有明显的“代表性偏差”特征，并应用HS模型解释我国小盘股反转效应比大盘股更明显的原因。

然而，上述模型都在事前假设投资者的心理偏差以及市场中投资者的类型，使得模型的解释力有限，模型之间也难以形成统一的框架。其次，这些模型构建的投资策略通常难以找到合适的代理变量，以反映模型假设的行为偏差。最后，这些模型研究的更多的是股价最终形成的均衡结果，而没有反映市场从初始状态向均衡演化时，决策各方相互影响的过程。相比一般均衡，博弈论的理论框架更适合探讨决策者之间的策略互动，因为纳什均衡在交换经济中更加广泛[12]。问题在于，纳什均衡对参与者的理性提出了更高的要求，即决策者不仅时刻以自身利益最大化为目标，并且在博弈环境中具有完美的判断和预测能力，而动量效应与反转效应恰恰是理性人假说无法解释的金融市场异象。

基于上述种种矛盾，本文为了探讨有限理性的投资者在市场中的相互影响，通过引入“演化博弈理论”的分析框架，研究股价动量与反转效应出现的原因以及实现均衡的过程。演化博弈理论的研究对象是非理性的群体性行为，并不要求决策者具有完全理性，相反，决策者通过反复的学习和模仿，最终形成一种所有决策者都不会做出改变的演化稳定策略，而市场也将达到一种演化稳定均衡的状态。相比于纳什均衡这一静态概念，演化稳定均衡更能体现动态调整的过程，故在预测群体行为方面更具现实性。在使用演化博弈理论研究股票市场已有文献方面，徐荣贞、蔡萌[13]对基本面与技术分析何者更优进行了演化博弈分析，指出在有效市场中基本面分析更优，而我国股市短期的股价大幅波动正是市场无效、投资者更多采取技术分析的结果。吴江、张辉[14]对机构投资者的羊群行为进行了演化博弈分析，指出机构投资者作为市场主体，为谋求自身利益最大化而进行反复模仿与学习，将可能导致羊群效应。可见，采用演化博弈模型来模拟动量效应与反转效应的动态调整过程不失为一种有益的尝试。

本文的研究意义主要包括以下几个方面：1将前景理论引入演化博弈理论的分析框架，考察心理因素对决策的影响，进一步放宽了对决策者理性的约束，使之更贴近现实。在前景理论的影响下，投资者买进或卖出股票的决策不仅依赖于未来的期望收益，还依赖于股价变化所引起的财富感知变化，而这恰恰是有限理性的决策者区别于达尔文自然选择理论中仅依靠突变和模仿调整行为的生物的关键所在。2相比BSV、DHS、HS等模型在心理学方面的假设，采用前景理论刻画投资者心理容易找到现实的代理变量，这就为后续基于理论模型的实证检验和投资策略建立提供了便利。3本文假设投资者是事前同质且非理性的，并将交易成本引入博弈支付矩阵，探讨交易成本的高低对投资者决策的影响，这实际上是从投资者决策分布结构动态演化的角度来探讨动量效应与反转效应的形成。除此之外，本文还探讨了投资者人数对动量效应和反转效应的影响。

二、研究假设与模型构建

考虑一个由M个事前同质的投资者构成的股票市场，允许卖空交易，模型包括以下假设：假设1：每个投资者在每个交易日t都拥有1单位的股票交易权，并在每个交易日都进行一次加仓买入行为（简称为“B策略”，概率为ptB∈[0，1]）或减仓卖出行为（简称为“S策略”，概率为pSt=1-ptB∈[0，1]）的博弈，全部投资者每天的博弈结果将形成收盘价Pt，这也是下个交易日的开盘价。假设2：投资者只关注当日的盈亏情况，并据此决定下个交易日是否改变策略。股市为T+1交易制度，且股票无分红。因此如果投资者加仓，那么只有收盘价Pt高于开盘价Pt-1才能获利;反之如果投资者减仓，那么只有收盘价Pt低于开盘价Pt-1才能获利。假设3：投资者对每日的盈亏存在财富感知，财富感知的高低受前景理论中“锚定效应”的影响，具体来说：相对某个较低参照股价，开盘价越高，则采取加仓策略的投资者从每单位股价上涨中获得的财富感知越少;相对某个较高的参照股价，开盘价越低，则采取减仓策略的投资者从每单位股价下跌中获得的财富感知越少。假设4：存在交易成本，包括两部分：1投资者搜寻交易对手耗费的时间成本，该成本随着采取相同策略的投资者人数的提高而增加;2投资者交易成功时支付的固定费用，包括交易手续费、印花税等。

根据上述四个假设，表1给出了该博弈的支付矩阵，其中数字代表如果交易对手（投资者II）采取第一行的某个策略时，自己（投资者I）采取左边一列的某个策略时所产生的效用。

该矩阵中各参数的含义如下：CpBt：采取B策略

的投资者搜寻交易对手的时间成本，其中C代表时间成本系数。当采取B策略的投资者与另一采取B策略的投资者在市场中相遇时，他们不能完成交易而必须去寻找采取S策略的投资者。因此，采取B策略的投资者人数越多，搜寻到S策略的投资者越困难，时间成本越高。CpSt：采取S策略的投资者搜寻交易对手的时间成本，定义同上。D：投资者交易成功时支付的固定费用，如手续费、印花税等。φt：交易日t的收盘价Pt相比开盘价Pt-1每上涨1单位，投资者因此而产生的财富感知系数，形式满足φt=λφ（Pt-1-P∗）-μφ，其中λφ代表投资者对股价上涨的风险厌恶系数，μφ代表股价上涨时投资者对财富变化的敏感性系数，P∗代表参考价格。当股价上涨时，投资者参考最近一个历史低点股价PL，不难发现∂φt/∂（Pt-1-P∗）<0，即φt与交易日t的开盘价高于最近一个历史低点股价的程度负相关。ηt：交易日t的收盘价Pt相比开盘价Pt-1每下跌1单位，投資者因此而产生的财富感知系数，形式满足ηt=λη（P∗-Pt-1）-μη，其中λη代表投资者对股价下跌的风险厌恶系数，μη代表股价下跌时投资者对财富变化的敏感性系数，P∗代表参考价格。当股价下跌时，投资者参考最近的一个历史高点股价PH，不难发现∂ηt/∂（P∗-Pt-1）<0，即ηt与交易日t的开盘价低于最近一个历史高点股价的程度负相关。Pt-Pt-1：交易日t的收盘价与开盘价之差，形式满足Pt-Pt-1=M（ptB-pSt），其中M代表投资者人数，假设股价变化幅度与投资者人数正相关。

用E（B，B）、E（B，S）、E（S，B）和E（S，S）分别代表投资者I取前一种策略、投资者II取后一种策略时，投资者I的效用，并定义“效用=交易成功的概率×交易成功时的财富感知-搜寻交易对手的成本”。故φtmax{Pt-Pt-1，0}-ηtmax{Pt-1-Pt，0}-D、ηtmax{Pt-1-Pt，0}-φtmax{Pt-Pt-1，0}-D分别代表交易成功时B策略、S策略投资者的财富感知。根据表1博弈支付矩阵可以得到，当ptB>pSt时：

根据演化博弈理论，博弈者并不需要事前知道以上支付矩阵中的参数，只需要对过去的博弈结果加以统计，通过反复试错便可得到参数的相关信息，从而对未来的决策进行修正，并最终达到演化均衡。

三、模型求解

接下来将讨论在每个交易日t，上述博弈的演化稳定策略。根据上述模型假设，采取B策略的投资者的期望总效用为：

采取S策略投资者的期望总效用为：

因此，所有投资者的平均总效用为：

由于ptB+pSt=1，故在交易日t，该演化博弈模型的复制动态方程为：

其中：τ代表演化时间，以区别交易日t。F[ptB（τ）]代表在交易日t整个投资者群体的演化速度[简写为F（ptB）]。满足F（ptB）=0且F（′ptB）<0的ptB是演化稳定策略中采取B决策的人数比重。显然，初始ptB与1/2的相对大小将对演化稳定策略产生影响，结果总结为表2。

表2中四个均衡点的复制动态相位图如图1所示。

表2的结果表明：1如果财富感知系数很高，那么演化均衡策略为纯策略B（pB=pB1=1）或S（pB=pB3=0），当市场达到这一均衡状态时，所有投资者都采取统一的加仓或减仓策略，市场交易将中断。这类似于我国股市中涨停或跌停的状态。2如果财富感知系数较高，那么演化均衡策略为混合策略，如果策略为（IB）=ptB2B+（1-ptB2）S，市场达到均衡时将有pB2M的投资者加仓，（1-pB2）M的投资者减仓，由于买方占优，股价将上涨;如果策略为（IS）=pB4B+（1-pB4）S，市场达到均衡时有pB4M的投资者加仓，（1-pB4）M的投资者减仓，由于卖方占优，股价将下跌。3如果财富感知系数很低，则没有演化稳定策略。4买卖双方均势的情况并不是演化均衡点，任意一方的投资者改变策略都将获利。

投资者在交易日t将根据表2中的演化均衡条件以及演化稳定策略的平均效用W决定选择何种交易策略。将四个演化均衡点ptB1、ptB2、ptB3和ptB4代入（5）式得到各ESS策略在演化均衡点的平均总效用：

由于演化稳定策略具有最大的平均效用，故表3给出了交易日t投资者最终选择的演化稳定策略。

四、模型结果分析：动量与反转效应的形成过程

本节将根据表3给出的演化稳定策略，讨论一段时期内投资者决策的演化过程以及演化过程中股价的变化，并揭示动量效应与反转效应的形成机理。假设市场初始p0B=1/2+ε（ε为一个微小扰动项）以及φ1>Q1，那么在交易日1，可能的演化路径有三条：

路径1.1：如果同时有η1>Q1，纯策略B与S都是可能的演化稳定策略，因为股价上涨或下跌的可能性都很大，其产生的财富感知都很高。此时，ε将影响演化的方向：如果ε>0，则买方占优，投资者更可能向B策略演化;如果ε<0，则卖方占优，投资者更可能向S策略演化。

路径1.2：如果同时有Q<η≤Q，混合策略（IS）是演化稳定策略，这是由于W（pB4）>W（pB1），采取混合策略（IS）在均衡时能获得更高的效用。

路径1.3：如果同时有η1≤Q2，由于卖方占优的演化均衡不存在，纯策略B是唯一的演化稳定策略。

不妨假设市场向纯策略B演化，演化均衡点为pB1=1，那么从交易日1开始，采取B策略的投资者将超过S策略的投资者，而股价也将上涨。需要注意的是，这并不意味着在交易日1可以直接达到演化均衡，能否达到演化均衡取决于初始采取B策略的投资者比重以及演化速度F（p1B）。由于φt随股价连续变化，因此存在一段时间t∈[1，t1），在这段时间内始终有φt>Q1。如果同时有ηt≤Q2，那么市场的演化稳定策略和演化均衡点将保持不变，采取B策略的投资者将随着时间的推移而增加，并推动股价上涨。

如果演化速度足够快，那么全部投资者都将统一采取B策略。此时交易将中止，但股价仍会继续上涨。从交易日t1开始，股价上涨导致Q2<φt≤Q1，纯策略B不再是演化稳定策略，ptB1=1也不再是演化稳定均衡点。此时，同样存在三条可能的演化路径：

路径2.1：如果ηt>Q1，混合策略（IB）是演化稳定策略，这是由于W（pB2）>W（pB3），采取混合策略（IB）在均衡时能获得更高的效用。此时演化均衡点将从pt=1下降至pt，采取B策略的投资者将减少，采取S策略的投资者将增加，但由于买方占优，股价仍会继续上涨。

路径2.2：如果Q2<ηt≤Q1，混合策略（IB）与（IS）都是可能的演化稳定策略。此时如果φt<ηt，则W（pB2）>W（pB4），（IB）是演化稳定策略;如果φ>ηt，则W（pB2）<W（pB4），（IS）是演化穩定策略。这里的含义是：当投资者采取混合策略时，均衡的平均效用不仅与财富感知系数有关，还与买卖双方的人数缺口|ptB-pSt|有关。由表2的结果不难发现，∂ptB2∂φt>0，∂ptB4∂φt<0，因此财富感知系数φt、ηt越高，均衡时人数缺口|pBt-pSt|越大，这会导致人数占优一方的投资者耗费大量的成本搜寻交易对手，但没有交易获利，从而抵消了高财富感知系数的好处;财富感知系数φt、ηt越低，人数缺口|ptB-pSt|越小，实际成交量将提高，均衡的平均效用也将随之提高。

路径2.3：如果ηt≤Q2，由于卖方占优的演化均衡不存在，故混合策略（IB）是唯一演化稳定策略。

如果投资者采取混合策略（IB），并以pt为演化均衡点，不妨假设在t∈[t1，t2）的交易日中，投资者逐渐从B策略转变为S策略，但由于买方仍占优，因而股价会继续上升。需要注意的是，在这一阶段，每个交易日的演化均衡点pB2都将发生变化，由于∂pB2/∂（P-P）=（∂pB2/∂φ）[∂φ/∂（P-P）]<0，因此随着股价的上升，pB2t将下降。

从交易日t2开始，φt≤Q2，买方占优的演化稳定均衡将不存在。此时，存在三条可能的演化路径：

路径3.1：如果η1>Q1，纯策略S是演化稳定策略，减仓的投资者将继续增加，股价将下跌。

路径3.2：如果Q2<ηt≤Q1，那么混合策略（IS）是演化稳定策略，减仓的投资者将继续增加，股价也将下跌。

路径3.3：如果ηt≤Q2，则不存演化稳定策略，买卖双方的相对人数以及股价的变化都无法预期，股市将处于震荡状态。

以上主要讨论了股价上涨的演化路径与条件，事实上当投资者在市场中博弈时，每个交易日的股价都存在上涨与下跌的可能，这取决于市场以哪个演化均衡点作为演化目标。图2给出了更详细的股价演化情况。

其中：向上的箭头代表股价上涨，向下的箭头代表股价下跌，虚线箭头代表股价震荡;箭头上的“B”“（IB）”“S”“（IS）”分别代表在一定时期内的演化稳定策略。例如：当股价沿着A→C→D→E的路径演化时，表明股价在t∈[t0，t2）呈上涨动量，在交易日t2反转，并在t∈[t2，t3）呈下跌动量;当股价沿着A→I→J→K的路径演化时，表明股价在t∈[t0，t1）呈上涨动量，先在交易日t1反转，并在t∈[t1，t2）呈下跌动量，后在交易日t2反转，并在t∈[t2，t3）呈上涨动量;当股价沿着A→L→M→N的路径演化时，表明股价在t∈[t0，t1）呈下跌动量，先在交易日t1反转，并在t∈[t1，t2）呈上涨动量，后在交易日t2反转，并在t∈[t2，t3）呈下跌动量;当股价沿着A→F→G→H的路径演化时，表明股价在t∈[t0，t2）呈下跌动量，在交易日t2反转，并在t∈[t2，t3）呈上涨动量。

综合上述分析，可以建立如下命题：

命题1：如果投资者因股价上涨（下跌）盈利而

产生的财富感知足够强，那么通过每天的重复博弈，就会逐渐形成一致的买入（卖出）股票的策略，从而推动股价持续上涨（下跌），产生动量效应。而在锚定效应的作用下，投资者因股价持续上涨（下跌）产生的财富感知逐渐减弱，从而逐渐改变策略，直至股价停止上涨（下跌）转为下跌（上涨），产生反转效应。

命题1包含以下几层含义：1投资者盈利产生的财富感知通过每天的重复博弈在市场中传递，影响其他投资者的决策，使越来越多的投资者产生趋同行为，从而形成股价持续的上涨或下跌，即动量效应;2当采取相同决策的投资者逐渐增多时，每个投资者搜寻交易对手的时间成本将提高，因此只有足够强的财富感知才能弥补成本，维持股价的动量效应;3由于锚定效应的存在，股价持续上涨或下跌将导致盈利的财富感知持续下降，当其不能弥补成本时，投资者将逐渐改变当前策略，导致动量减弱，直至出现反转。

通过上文的博弈分析还可以看出，“足够高”的财富感知要求φ>Q或η>Q，此时动量和反转才可能出现;而当φt≤Q2或ηt≤Q2时，由于财富感知系数过低，股价无论上涨还是下跌都不能使大部分投资者获利，投资者就无法通过每天的重复博弈形成演化稳定策略，动量与反转效应也无法出现，股价将陷入震荡状态。通过对Q2求关于C、D和M的偏导数，可以得到：

∂Q2/∂C>0，∂Q2/∂D>0，∂Q2/∂M<0（8）

综合上述分析建立如下推论：搜寻交易对手时间成本的提高、交易成功固定费用的降低以及投资者人数的减少，将阻碍股价动量效应与反转效应的形成，并导致股价陷入震荡状态。

值得注意的是，虽然对投资者而言，时间成本（C）的提高与固定交易费用（D）的提高都将导致决策效用的降低，但它们对动量和反转效应产生的影响相反。当时间成本提高时，采取相同决策的效用E（B，B）、E（S，S）将下降，而采取相反决策的效用E（B，S）、E（S，B）不变，这意味着时间成本的上升对“顺势而为”的投资者不利，而对“逆势而动”的投资者有利，从而阻碍动量的持续;当固定交易费用提高时，尽管所有决策的效用都降低了，但采取相同决策的效用E（B，B）、E（S，S）降低的幅度低于采取相反决策的效用E（B，S）、E（S，B），这是由于固定费用只有在交易成功时才会发生，因此市场中采取趋同策略的投资者越多，交易成功的几率越小，固定费用提高造成的损失越小，故对“顺势而为”的投资者有利，对“逆势而动”的投资者不利，从而推动动量的持续。

五、动量效应与反转效应的影响因素

在上文命题与推论的基础上，进一步讨论时间成本、固定交易费用以及投资者人数这三种因素如何通过影响演化速度F（pBt）和演化均衡点pB2t与pB4t，进而影响动量与反转效应的显著性。由于模型的对称性，这里只讨论上涨动量与顶部反转的情况。

1.搜寻交易对手的时间成本（事前成本）。对F（ptB）和ptB2求关于C的偏导数，可以得到：

∂F（ptB）/∂C<0，∂ptB2/∂C<0（9）

（9）式表明，当搜寻交易对手的时间成本提高时，将阻碍投资者向均衡点演化，因此整个市场的演化速度下降，并在一定时间内可能无法达到演化均衡点，股价上升与下降的速度也将减慢。同时，时间成本的提高将导致演化均衡点pB2t向1/2移动，也就是说，演化均衡时采取B策略的人数将减少，由于股价变化的幅度与采取两种策略的投资者人数缺口|ptB-ptS|正相关，因此ptB2的下降会降低股价上涨的幅度。由于搜寻交易对手的时间成本属于事前成本，故综合上述分析可以建立如下命题：

命题2：事前成本的提高将降低股价上涨（下跌）的速度与幅度，导致股价动量效应的程度减弱，反转效应发生的可能性提高。

2.交易成功支付的固定费用（事后成本）。再对F（ptB）和ptB2求关于D的偏导数，可以得到：

∂F（ptB）/∂D>0，∂ptB2/∂D>0（10）

（10）式表明，当交易成功支付的固定费用提高时，演化速度将提高，演化均衡点pB2也将向1移动。

原因正如上文所述：如果股价当前处于上涨趋势，那么对投资者而言，当固定费用提高时，采取与市场趋势相同的B策略比相反的S策略损失更小，因为交易成功率越低，越不必支付这笔固定费用。这种决策选择将导致股价被继续推高，且推高的速度也将加快。由于交易成功支付的固定费用属于事后成本，故综合上述分析可以建立如下命题：

命题3：事后成本的提高将提高股价上涨（下跌）的速度与幅度，导致股价动量效应的程度增强，反转效应发生的可能性降低。

3.投资者人数。最后对F（ptB）和ptB2求关于M的偏导数，可以得到：

∂F（ptB）/∂M>0，∂ptB2/∂M>0（11）

（11）式表明，当投资者人数增加时，演化速度将提高，演化均衡点pB2也将向1移动，因为投资者人数的增加能推动股价更大幅度地上涨（下跌），从而使采取买进（卖出）策略的投资者获利更多，这会促使投资者更快地向演化均衡点移动，且在均衡时采取B策略的投资者人数增加。由于投资者人数的多少反映了该只股票成交量的大小，故综合上述分析建立如下命題：

命题4：股票成交量的提高将提高股价上涨（下跌）的速度与幅度，导致股价动量效应的程度增强，反转效应发生的可能性降低。

六、仿真分析

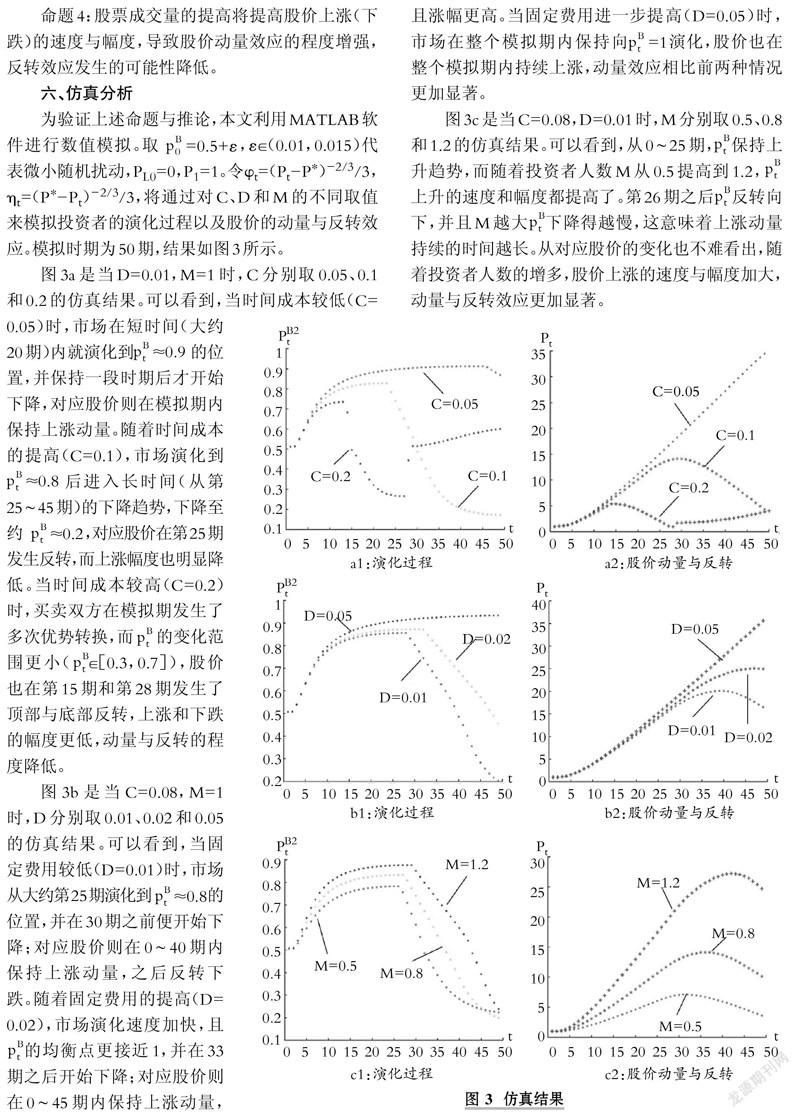
为验证上述命题与推论，本文利用MATLAB软件进行数值模拟。取p0B=0.5+ε，ε∈（0.01，0.015）代表微小随机扰动，P=0，P=1。令φ=（Pt-P∗）-2/3/3，ηt=（P-Pt）/3，将通过对C、D和M的不同取值来模拟投资者的演化过程以及股价的动量与反转效应。模拟时期为50期，结果如图3所示。

图3a是当D=0.01，M=1时，C分别取0.05、0.1和0.2的仿真结果。可以看到，当时间成本较低（C=0.05）时，市场在短时间（大约20期）内就演化到ptB≈0.9的位置，并保持一段时期后才开始下降，对应股价则在模拟期内保持上涨动量。随着时间成本的提高（C=0.1），市场演化到pB≈0.8后进入长时间（从第t25～45期）的下降趋势，下降至约ptB≈0.2，对应股价在第25期发生反转，而上涨幅度也明显降低。当时间成本较高（C=0.2）时，买卖双方在模拟期发生了多次优势转换，而ptB的变化范围更小（pB∈[0.3，0.7]），股价也在第15期和第28期发生了顶部与底部反转，上涨和下跌的幅度更低，动量与反转的程度降低。

图3b是当C=0.08，M=1时，D分别取0.01、0.02和0.05的仿真结果。可以看到，当固定费用较低（D=0.01）时，市场从大约第25期演化到ptB≈0.8的位置，并在30期之前便开始下降;对应股价则在0～40期内保持上涨动量，之后反转下跌。随着固定费用的提高（D=0.02），市场演化速度加快，且ptB的均衡点更接近1，并在33期之后开始下降;对应股价则在0～45期内保持上涨动量，且涨幅更高。当固定费用进一步提高（D=0.05）时，市场在整个模拟期内保持向ptB=1演化，股价也在整个模拟期内持续上涨，动量效应相比前两种情况更加显著。

图3c是当C=0.08，D=0.01时，M分别取0.5、0.8和1.2的仿真结果。可以看到，从0～25期，ptB保持上升趋势，而随着投资者人数M从0.5提高到1.2，ptB上升的速度和幅度都提高了。第26期之后ptB反转向下，并且M越大ptB下降得越慢，这意味着上涨动量持续的时间越长。从对应股价的变化也不难看出，随着投资者人数的增多，股价上涨的速度与幅度加大，动量与反转效应更加显著。

七、结论

本文的研究意义在于以演化博弈理论为工具，结合前景理论与交易成本理论，解释了动量效应与反转效应的成因。通过本文研究，可以得到以下结论：

1.动量效应与反转效应不是孤立的现象，而是在一定条件下可以相互转化的共生现象。转化的条件是投资者采取趋同的追涨杀跌策略而产生的财富感知与交易成本的相对高低：若财富感知相对较高，投资者将坚持这一策略，产生动量效应;若财富感知相对较低，投资者将逐渐改变策略，产生反转效应。

2.由于锚定效应的存在，以股价偏离历史高点（低点）的程度筛选“动量—反转”组合不失为一种可行的选股策略。偏离程度越低的股票为动量组合，因为未来延续当前趋势的可能性越大;偏离程度越高的股票为反转组合，因为未来延续当前趋势的可能性越小。这种策略构建的方式不同于基于股票历史业绩而筛选的“赢家—输家”组合，是对股票未来继续上涨（下跌）能力的预期，因此更能反映由投资者心理因素导致的动量与反转效应的形成。

3.事前成本越低，动量效应越显著。随着互联网技术的不断发展，投资者搜寻交易对手越便利，采取趋同策略越容易获利。如果市场监管者希望抑制股市的波动，则应该建立更加完善、丰富的金融投资市场，增加投资渠道，使投资者在股市中采取趋同策略的机会成本提高，而非提高印花税等交易费用，因为这类交易费用属于事后成本，事后成本的提高反而可能加大股市的波动。

4.股票的成交量对股价的动量效应具有推波助澜的作用。对动量投资者而言，选择高股本、高成交量的蓝筹股更容易获得动量收益;而对于反转投资者而言，选择小股本、低成交量的小盘股更容易获得反转收益。

当然本文也存在不足之处，比如在博弈模型中只考虑了买卖两种策略，而实际上还有持股观望等策略，在演化博弈模型中可通过增加新的投资决策，例如持股观望，或者考虑加入做市商的影响，可能会得到更加丰富的研究结论。基于模型建立投资组合的策略也是下一步重点研究的方向。

主要参考文献：

[1] Fama E.，French K.. Multifactor explanations of asset pricing anomalies[J].Journal of Finance，1996（1）：55～84.

[2] Jegadeesh N.，Titman S.. Returns to buying winners and selling losers：Implications for stock market efficiency[J].Journal of Finance，1993（1）：65～91.

[3] De Bondt W. F. M.，Thaler R.. Does the stock market overreact？[J].Journal of Finance，1985 （3）：793～805.

[4] Barberis N.，Shleifer A.，Vishny R.. A model of investor sentiment[J].Journal of Financial Economics，1998（3）：307～343.

[5] Barberis N.，Huang M.，Santos T.. Prospect theory and asset prices[J].The Quarterly Journal of Economics，2001（1）：1～53.

[6] Kahneman D.，Tversky A.. Prospect theory：An analysis of decision under risk[J].Econometrica，1979（2）：263～291.

[7] Daniel K.，Hirshleifer D.，Subrahmanyam A.. Investor psychology and security market under and overreactions[J].Journal of Finance，1998（6）： 1839～1885.

[8]HongH.，SteinJ..Aunifiedtheoryofunderreaction，momentum trading，and overreaction in asset markets[J].Journal of Finance，1999（6）：2143～2184.

[9]魯臻，邹恒甫.中国股市的惯性与反转效应研究[J].经济研究，2007（9）：145～155.

[10]张荣武，赵行亮.经济周期、前景理论与BHS资产定价模型修正[J].财经理论与实践，2011（4）：51～55.

[11]谭小芬，林雨菲.中国A股市场动量效应和反转效应的实证研究及其理论解释[J].中国软科学，2012（8）：45～57.

[12]赵山.纳什均衡与一般均衡的关系研究[J].数量经济技术经济研究，2005（1）：138～143.

[13]徐荣贞，蔡萌.股票投资策略选择的演化博弈与仿真研究[J].财会月刊，2010（9）：65～66.

[14]吴江，张辉.机构投资者羊群行为的演化博弈分析[J].系统管理学报，2013（4）：466～471.