基于SIMION的微通道板增益研究

赵一帆

摘 要：本研究利用SIMION（离子光学问题模拟软件）来模拟两片微通道板及其二次电子发射过程，并分析微通道板增益的影响因素。首先利用SIMION的几何定义功能模拟微通道板电场和微通道。然后，修改SIMION提供的二次电子发射程序。本研究包含三次模拟，分别测试电压、斜切角和直径对微通道板增益的影响。第一次模拟改变电压。在不同能量下的三次实验表明，微通道板增益与电压成正比。第二次模拟改变斜切角，并得到在不同能量和电压下使微通道板增益最大的四个斜切角角度。第三次模拟改变微通道板的直径，得出微通道板的直径与增益呈反比的结论。三次模拟的结果均符合现有理论，且在合理范围内。因此，本研究利用SIMION建立的两片微通道板模拟是精确的。

关键词：微通道板;SIMION;二次电子发射;离子模拟

1 引言

微通道板（MCP）广泛应用于粒子检测。它与电子倍增管相似，它们都通过二次电子发射放大单个粒子的信号。微通道板由铅玻璃制成，从一个面到另一个面有大约10000000个微通道的规则阵列。在MCP的前后表面是一层金属涂层，用作输入和输出电极。微通道板的长径比在40到100之间。图1显示了MCP的基本结构。除直通道微通道板外，还有两片微通道板和三片微通道板（见图2）本论文旨在利用SIMION评估电压、斜切角和直径对两片微通道板增益的影响。目前，人们一致认为微通道板增益与电压成正比，5°和15°之间的斜切角产生最大增益。同时，MCP增益与长径比成正比，与直径成反比。这些结果一般来源于实验，并未用SIMION对MCP增益进行全面的研究。

2 理论模型

2.1 微通道板概述

微通道板通过施加电场，使每个通道都充当电子倍增管。由于通道与板成一定角度，进入MCP的粒子一定会撞到管壁，產生二次电子，并在场强作用下继续前进，形成“电子雪崩”最终放大输入信号。两片微通道板由两个相互旋转180°的单通道MCP组成。图3是两片MCP的示意图。斜切角是微通道板和微通道板两端面垂直轴线的角度，使微通道板增益最大的斜切角在5°到15°之间。图4显示了两片MCP中的斜切角θ。斜切角有效地减少了离子反馈，增加了入射电子撞击通道表面的几率。在两片MCP中，输入电子在第二个板中发生“电子雪崩”。两板间距离为50-150μm。

1979年，Wiza用电压、二次电子初始能量和长径比建立微通道板增益模型。Wiza发现，在两片MCP中，总通道电压与增益成正比。2017年，Chen等人研究了几何参数对微通道板增益的影响。Chen的研究指出：12度的斜切角使MCP增益最大，大于12度的角度会降低微通道板的增益。两片微通道板的增益可以达到10^8至10^9。

2.2 SIMION概述

SIMION是一个离子光学模拟程序。它使用离子光学工作台（ion optics workbench），工作台的总体积为8立方公里。SIMION利用电势阵列（potential array）定义了电极的几何形状以及电势。几何定义是一种高级SIMION功能，允许用户定义复杂的电极。gem文件应该定义被创建的电势阵列大小、对称性、镜像、类型（电或磁）和磁缩放因子。SIMION可以通过用户编程来扩展，本研究使用lua语言编程。SIMION提供一个模拟二次电子发射的程序。此示例允许用户使用数学表达式计算曲面法向并得到二次电子轨迹。这一示例中的其他参数包括能量模式、最大时间（电子可以做多少次发射）和电子击中表面的次数。本研究修改了该程序。

3 微通道板增益的影响因素研究

3.1 模拟步骤

首先利用几何定义模拟微通道板电场和管壁。电场文件是一个3000*150*50（x*y*z）的平面非镜像空间，包含两个三维电极。左边的电极设置为-100伏，右边的电极可调。电场几何文件以0.001的毫米/网格单位的比例投影到工作台上。管壁文件再次定义了一个平面非镜像的3000*150*50（x*y*z）空间，其中有两个外半径为12个网格单位和可调内半径的通道管。图5是X-Y平面上两个通道管的示例，斜切角为图5中θ。

二次电子发射的模拟使用了SIMION二次发射示例并进行修改。该示例允许用户使用数学表达式计算法向向量，数学表达式为左管：

nx=（y-10-x·tan（θ°））·cos（θ°）·sin（θ°）

ny=（y-10-x·tan（θ°））·cos（θ°）·cos（θ°）

nz=25-z

右管：

nx=-（y-10-（2000-x）·tan（θ°））·cos（θ°）·sin（θ°）

ny=-（y-10-（2000-x）·tan（θ°））·cos（θ°）·cos（θ°）

nz=25-z

nx，ny，nz表示法向向量，θ为斜切角。本研究修改了判断是否发生二次电子发射的函数，只要（y-10-（300-x）·tanθ）2+（z-25）2大于r2，r为内径，就发生二次电子发射。最后，由于二次发射示例仅模拟一个输入电子产生一个二次电子的情况，因此需要新变量来表示产生的电子的总二次数量，即微通道板增益。新变量表示电子每次撞击表面时产生的电子数，增益等于总电子数乘以该变量乘以一个系数，使增益数接近现实情况。

3.2 电压对增益的影响

该模拟测量微通道板增益如何随电压的增加而变化的。在每次试验中，能量和斜切角是固定的。如前所述，随着电压的增加，MCP增益预计会增加。

测试1

表1为本次模拟的参数。

图6是这次试验的结果。从图中可以看出，微通道板的增益与施加的电压成正比。此图的形状类似于指数函数图，在较高电压下增益增加得更快。图7显示了低电压（低于1300V）下的电压与增益。该图是一条平滑曲线，其特征与图6相同。

测试2

参数见表2。图8是这次试验的结果。在较高的能量下，增益仍然与电压成正比，曲线仍然类似于指数函数。当电压低于1300V时，电压与增益的关系也是如此（图9）。

测试3

本测试参数见表3。图10显示了这次试验的结果。在E=50eV时，曲线图与之前的试验相似。然而，如图11所示，低电压下的电压-增益图不平滑。

3.3 斜切角对增益影响

此模拟测量微通道板增益随斜切角θ的变化。在每一个能级上测试了三种电压：800V、1500V和2200V。该模拟的目的是寻找使微通道板在不同能量和电压下的增益最大的斜切角。超过16度的角度无法测量的，因为这样的电势阵列SIMION无法处理。微通道板的内径为7个网格单元，外径为12个网格单元。

测试1

本测试在能量等于20ev的情况下进行。图12、13、14分别显示了800V、1500V和2200V电压下的斜切角与增益的关系。从图中可看出，在800V和1500V时增益最大的斜切角不确定。在2200V时，增益在16度的信道偏角下略有下降。因此，15度角使微通道板增益最大。

测试2

该试验在能量为40eV、电压为800V、1500V和2200V时进行。图15、16、17显示了结果。在图15中，微通道板增益在14度角处明显达到峰值。因此，电压为800v时，14度的斜切角使MCP增益最大。在1500V时，使增益最大的角度不确定（图16）。在2200V时，15度的偏角使MCP增益最大（图17）。

测试3

该测试能量等于50eV。图18、19、20为V=800V、1500V和2200V下的结果。在V=800V和2200V下，最大微通道板增益的角度是不确定的（图18、20）。如图19所示，在V=1500V时，最大化增益的斜切角为15度。

3.4 直径对增益的影响

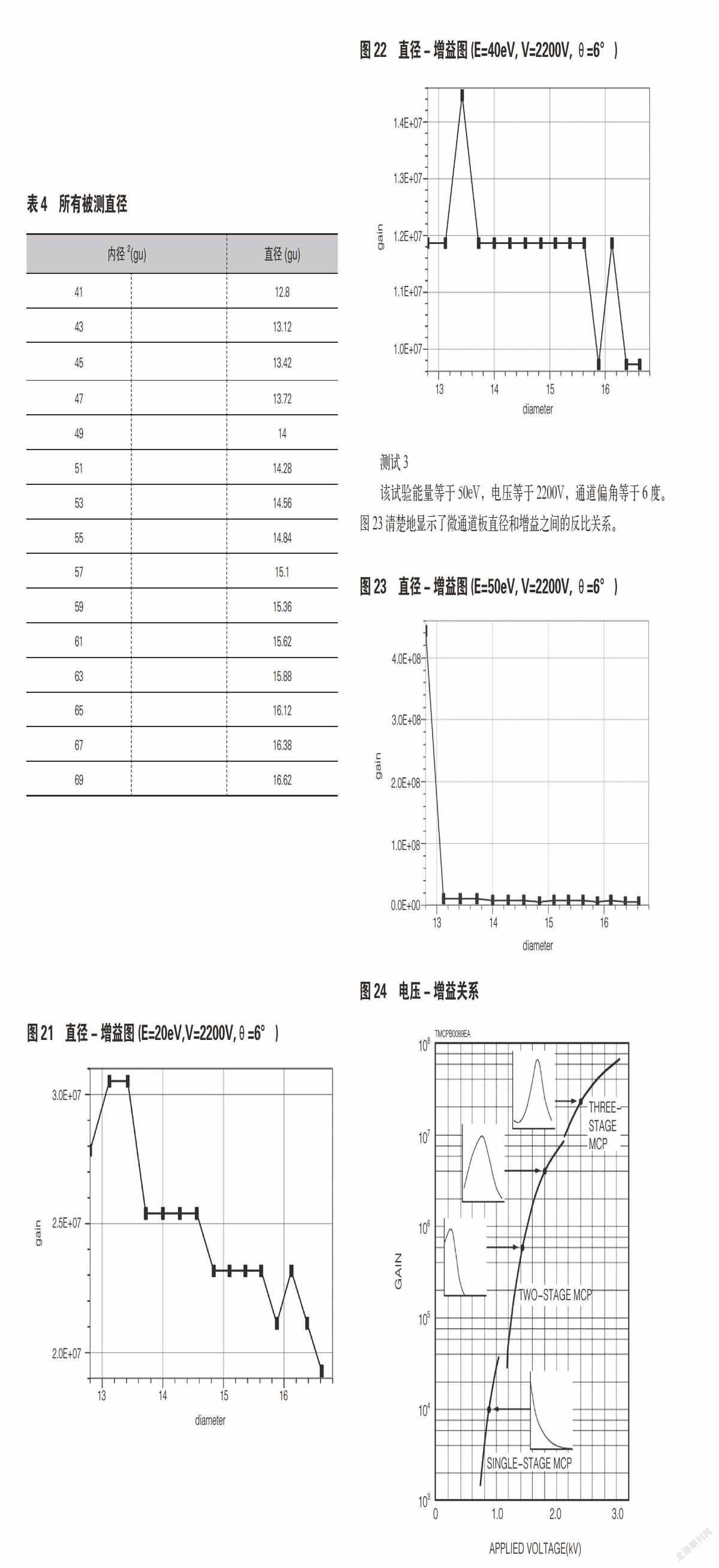
此模拟测量直径对增益的影响。直径通过内径变化而变化。表4显示了测量的所有直径。根据先前的研究，随着直径的增大，微通道板的增益会下降。

测试1

该测试在能量为20eV，电压为2200V，斜切角为6度的条件下进行。图21显示了结果。如图所示，除了直径等于12.8和15.88外，mcp增益与直径成反比。

测试2

此试验能量等于40eV，电压等于2200V，斜切角等于6度。如图22所示，微通道板增益从1.18e+07降低到1.0e+07以下。

测试3

该试验能量等于50eV，电压等于2200V，通道偏角等于6度。图23清楚地显示了微通道板直径和增益之间的反比关系。

4 数据分析

4.1 电压

2.2的结果表明，微通道板的增益与电压成正比，这与Wiza等人的实验结果一致，证明了本文模拟的准确性。

然而，根据Hamamatsu的研究，两片微通道板的电压-增益曲线是弯曲的（见图24）。本文得到的电压增益曲线与Hamamatsu的实验结果不符。这个问题可以通过模拟产生的二次电子的轨迹来解决，因为该模拟提供了作为增益产生的电子数量的精确数据。

4.2 斜切角

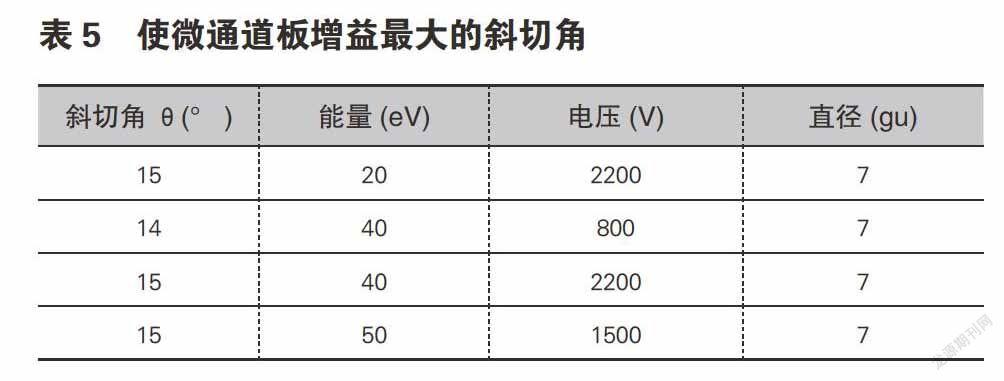
改变斜切角的模拟产生四个使微通道板增益最大的角度（见表5）。根据Chen等人的研究，通道偏角在5到15之间时，MCP增益最大。因此，本文得到的结果是合理的。

对于斜切角不确定的情况，应当测试大于16的角度，使本研究结论更全面。

4.3 直径

测试结果表明，微通道板的增益与直径成反比。这一结果Eberhardt、Chen等人建立的增益模型一致。通过模拟二次电子的运动轨迹，可以改善与直径和增益的反比关系不一致的数据点。

5 总结

在微通道板增益的研究中，本研究利用SIMION模擬了两片微通道板的通道管、放置管的电场和二次电子发射过程。利用几何文件模拟了两片MCP的通道管和电场，而二次发射过程修改了SIMION提供的二次发射实例。

模拟结果表明，MCP增益与电压成正比，与通道直径成反比，并发现了四个使增益最大的斜切角。所得结果与现有的微通道板增益理论相吻合，在合理的范围内。因此，利用SIMION模拟两片微通道板是成功的。未来的研究可以改进本严谨所使用的程序来模拟产生的二次电子的轨迹。

参考文献：

[1] Bolton， Paul， et al. “Instrumentation for diagnostics and control of laser-accelerated proton （ion） beams.” Physica medica， vol.30， no.3， Oct. 2013， pp. doi： 10.1016/j.ejmp.2013.09.002

[2] Chen， Lin， et al. “The Gain and Time Characteristics of Microchannel Plates in Various Channel Geometries.” IEEE Transactions on Nuclear Science， vol. 64， no. 4， 2017， pp. 1080-1086.， doi：10.1109/tns.2017.2676010.

[3] Eberhardt， Edward H. “Gain Model for Microchannel Plates.” Applied Optics， vol. 18， no. 9， 1979， p. 1418.， doi：10.1364/ao.18.001418.

[4] Fraser， G.w. “The Ion Detection Efficiency of Microchannel Plates （MCPs）.” International Journal of Mass Spectrometry， vol. 215， no. 1-3， 2002， pp. 13-30.， doi：10.1016/s1387-3806（01）00553-x.

[5] “Long Life Microchannel Plates.” Optimacorp.co， www.optimacorp.co.jp/BurleEO/MCP.htm.

[6] Manura， David， and David A. Dahl. SIMION 8.0 User Manual. Scientific Instrument Services， 2007.

[7] “MCP Assembly.” Hamamatsu Photonics， www.hamamatsu.com/resources/pdf/etd/MCP_TMCP0002E.pdf

[8] “Microchannel Plates.” Delmar Photonics， www.dmphotonics.com/MCP_MCPImageIntensifiers/microchannel_plates.htm

[9] Taylor， Richard Cordia， et al. “Maximizing the Quantum Efficiency of Microchannel Plate Detectors： The Collection of Photoelectrons from the Interchannel Web Using an Electric Field.” Review of Scientific Instruments， vol. 54， no. 2， Feb. 1983， pp. 171-176.， doi：10.1063/1.1137365.

[10] Tkachenko， Nikolai V. “Time Correlated Single Photon Counting.” Optical Spectroscopy， 2006， pp. 151-169.， doi：10.1016/b978-044452126-2/50032-0.

[11] Wiza， Joseph Ladislas. “Microchannel Plate Detectors.” Nuclear Instruments and Methods， vol. 162， no. 1-3， 1979， pp. 587-601.， doi：10.1016/0029-554x（79）90734-1.