斜放网格棱柱面密肋折板网壳的动力特性分析

朱锐 张华刚 陈寿延 姜岚 唐攒辉

摘 要：为了解斜放网格混凝土拟柱面密肋折板网壳动力特性，采用有限元法计算39个算例，对比了周边支承和拱脚支承屋盖的自振频率与振型，通过有限元参数化分析考虑结构的矢跨比、支座约束、斜向密肋梁刚度、脊线梁刚度、主拱梁刚度、边梁刚度、屋面板厚度对结构自振频率影响。分析表明：与下部结构协同工作时，周边支承对屋盖整体刚度提升较大;矢跨比对屋盖振动基频的影响较小，较大矢跨比会减弱端隔面外刚度，建议矢跨比取1/6Symbol～A@

1/4;支座约束对屋盖整体刚度的提升很大;提高斜向肋刚度有利于提高屋盖整体刚度，建议斜向肋截面高度取屋盖跨度的 1/60Symbol～A@

1/45;脊线梁截面刚度在屋盖的整体刚度中贡献较小，建议脊线的截面高度按构造确定;主拱刚度对屋盖整体刚度贡献较大，建议主拱截面高度取屋盖跨度的 1/51Symbol～A@

1/40; 边梁刚度在整体结构中贡献不大，可取边梁跨度的1/20Symbol～A@

1/15为边梁的截面高度;屋面板作为结构刚度储备在满足使用标准的情况下不应取值过大。

关键词：混凝土;斜放网格密肋折板网壳;支座约束;共同工作;动力特性;参数分析

中图分类号：TU311.3

文献标识码： A

我国经济建设到现今阶段，对建筑物的经济性、耐久性的要求越来越高，而混凝土结构比钢结构有着后期维护费用低的巨大优势，尤其适应在我国的广大南方以及沿海高湿度地区。但混凝土结构的最大缺点就是自重大，于是国内外专家开展了对自重轻的混凝土结构的探索之路。

薄壳结构具有自重小、跨度大、传力途径合理等优点，上世纪80年代前被广泛应用于建筑工程中，并为我国空间结构的发展奠定了基础[1]。近年来对薄壳结构的研究，或在于计算理论，相关文献较多[2];或者在于结构找形，以便充分发挥壳体的薄膜效应[3-4];或者在于纤维编织网增强混凝土等新材料的应用，以利于复杂曲面壳体的施工[5-6]。由于混凝土薄壳的施工支模较为繁琐，因此近年来，钢-混凝土组合结构是壳体发展的重要方向之一，出现了钢-混凝土组合网壳结构[7-8]、局部单双层混合网壳结构[9-10]和组合带肋壳结构[11]等。WONG[12]等提出的组合壳结构，将带肋钢壳通过布置在肋上的长螺栓与混凝土连接，钢壳既参与受力，又是混凝土浇筑的模板，致使钢壳的承载力及其屈曲行为在施工阶段尤为重要，当两者共同工作后，长螺栓会成为影响结构承载力的关键因素[13]。上述研究工作对推动壳体结构的发展是有利的。

为了使壳体更便于施工支模，张华刚等运用组合结构的思想将空间曲面切割为平面后再网格化，提出了混凝土折板式网壳结构，即结构由密肋平板在脊（谷）线处交汇构成[14]。其中人字形拱网壳的应用面积已达1.2万余平方米，有较好的适应性和技术经济指标[15]，齐卫东等[16-17]的研究表明，屋盖与下部结构宜共同分析，以便合理确定建筑顶层结构的承载力及抗侧刚度，方强等[18-20]还开展了拟扁网壳和幕形网壳的静动力性能分析，表明结构具有明确的传力途径和空间工作能力。

正交正放网格棱柱面网壳可以看作是由折线拱构成的单向传力结构，柳勇斌等的分析表明，纵向脊线几乎不影响网壳的整体刚度及承载力[21]。为提高结构的空间效应，本文将网格斜放，以使密肋平板的荷载能分配至纵向脊线上，基于动力有限元基本理论[22]做结构动力特性分析，并考察矢跨比、支座約束、斜向肋肋刚度、脊线刚度、主拱刚度、边梁刚度、屋面板厚度和下部结构协同工作下考虑山墙框架对结构动力特性的影响，以期为这种结构的工程应用提供参考。

1 算例情况及有限元模型

1.1 算例情况

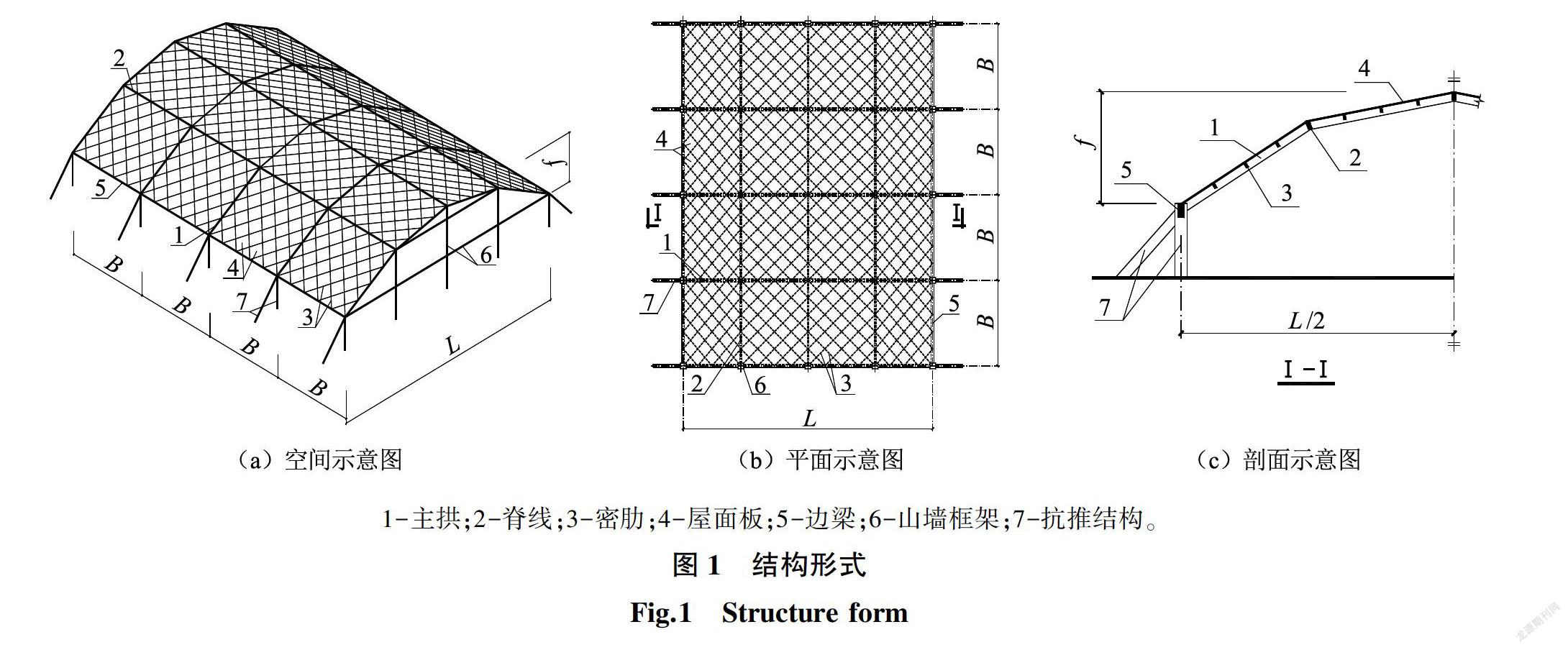
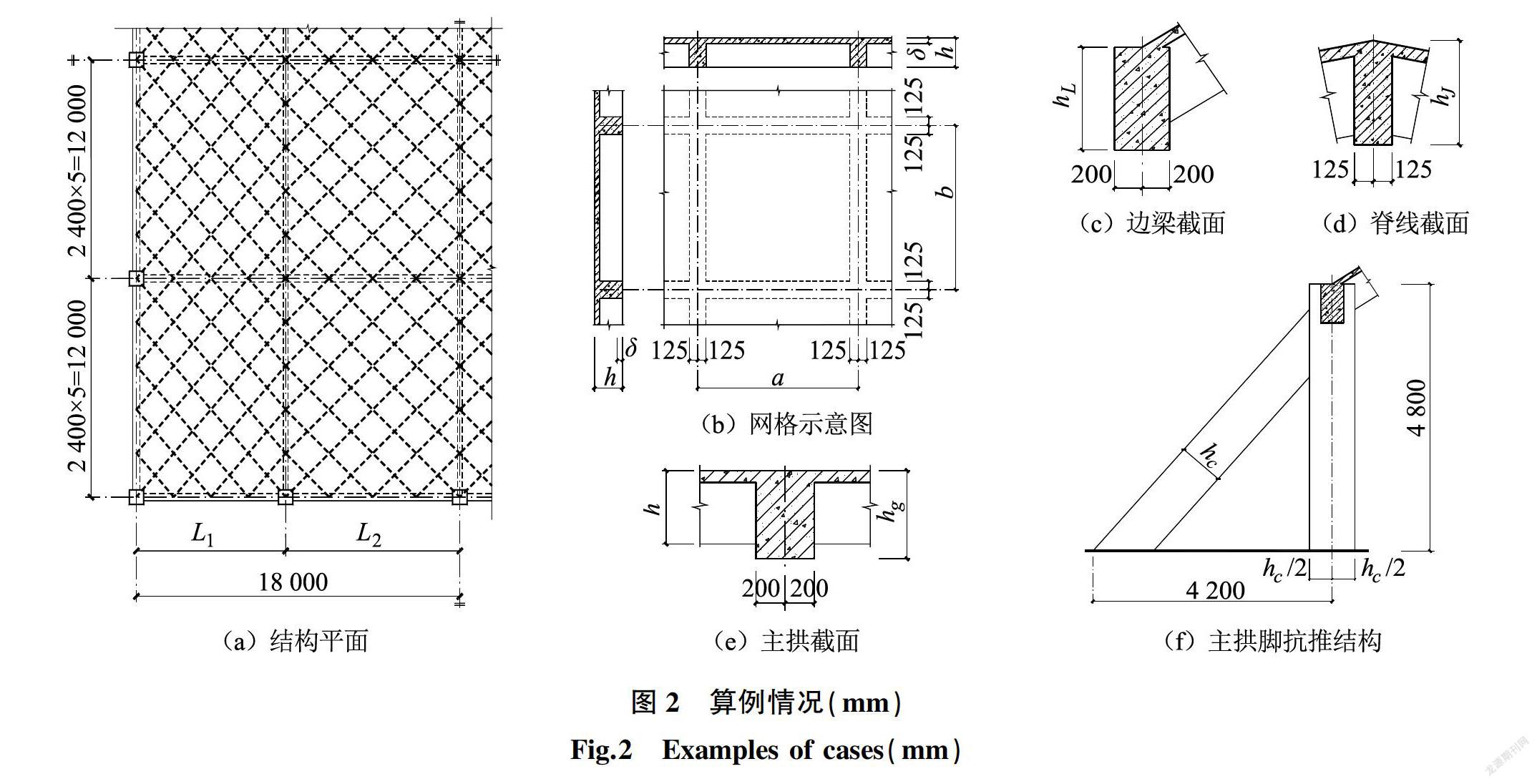
取屋盖跨度为L=36 m，纵向长度为48 m，主拱间距B=12 m，其结构形式如图1所示，全部算例的结构布置及密肋板的网格情况如图2所示，每段边梁被划分成5个网格，主拱的每个折线被划分为4个网格，由于边梁和主拱的网格长度不一致，因此密肋平板网格斜交斜放。

本文的全部分析算例情况如下：

1）基本算例

不考虑抗推支座影响做自由振动分析，即计算时主拱拱脚按固支考虑，但计及脊线在山墙处是否有支承的影响。脊线在山墙处支承时，脊线两端设柱且柱脚嵌固并与主拱拱脚同标高。屋盖矢高f=7.2 m，密肋截面高度h=0.5 m，屋面板厚度δ=60 mm，主拱和边梁的截面高度hg和hL均取0.6 m，脊线截面高度hJ=0.55 m。山墙框架腹杆截面尺寸为0.4 m×0.4 m、中弦剖面截面尺寸均为0.4 m×0.5 m，下弦横截面尺寸为0.4 m×0.6 m。

2）参数化分析算例

在基本算例基础上改变单一变量来做对基频影响的参数化分析：

（1）改变结构的矢跨比分析5个算例，分别取屋盖矢高f为12.0 m、9.0 m、7.2 m、6.0 m和4.5 m，即结构矢跨比由1/3降低至1/8，以考察矢跨比对结构基频的影响。

（2）取主拱及边梁的截面高度hg和hL均为1.0 m，脊线截面高度hJ=0.95 m，斜向肋截面高度取h为0.5 m、0.6 m、0.7 m、0.8 m和0.9 m，以考察其刚度对屋盖基频的影响。

（3）仅改变主拱的横截面高度hg以考察其刚度对基频的影响，且hg按0.1 m的级差由0.6 m增大至1.1 m，相当于hg取屋盖跨度的1/60Symbol～A@

1/33，共计算6个算例。

（4）对于脊线刚度影响的算例，固定主拱截面高度hg=1.1 m，脊线的横截面高度hJ按0.1 m的级差由0.55 m增大至1.05 m，共计算6个算例。

（5）在基本算例基础上，仅改变边梁的截面高度hL计算5个算例，且hL按级差0.1 m由0.6 m增大至1.0 m，相当于hL取边梁自身跨度的1/20Symbol～A@

1/12。

（6）仅分别取屋面板厚度δ=60 mm、80 mm、100 mm、120 mm计算4个算例，以考察屋面板厚度对屋盖基频的影响。

3）考虑支座抗推刚度对屋盖自振频率影响的算例

基于结构的受力特性，屋盖的推力将最终传递至主拱拱脚，因此实际工程应用时需要在主拱的拱脚设置抗推结构。本文选定图2（f）所示的抗推结构，在基本算例基础上，固定抗推构件的截面宽度为0.6 m，通过调整其横向截面高度hc为0.6 m、0.8 m、0.9 m、1.0 m、1.2 m，来考察抗推结构的刚度变化对屋盖动力特性的影响。

1.2 结构有限元模型

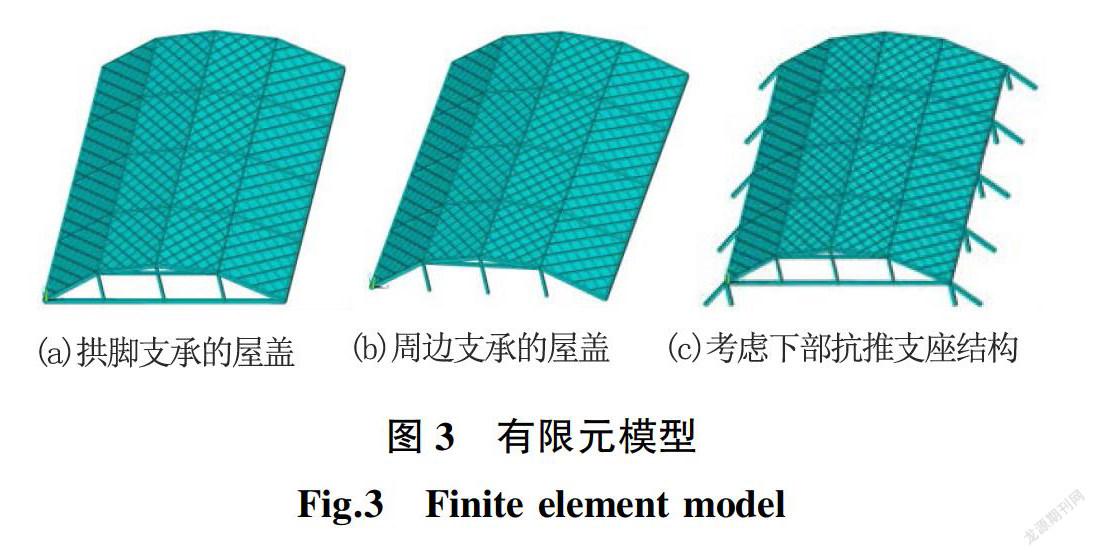
除屋面板采用板壳单元外，其余构件均采用空间梁单元，且板壳单元与梁单元的中性层重合，有限元节点主要采用了自然节点，在主拱拱脚处固定约束了节点的全部位移。计算时将外加荷载和屋盖自重转换为质量，通过质量单元施加在有限元模型上，外加荷载均为3.35 kN/m2，此外加荷载满足恒活组合荷载的情况。混凝土的弹性模量取Ec=3×104  N/mm2，泊松比取ν=0.2，在动力特性分析中采用分块兰索斯（Block Lanczos）法来求解结构的特征方程。有限元模型如图3所示。

2 结构的动力特性

2.1 自振頻率

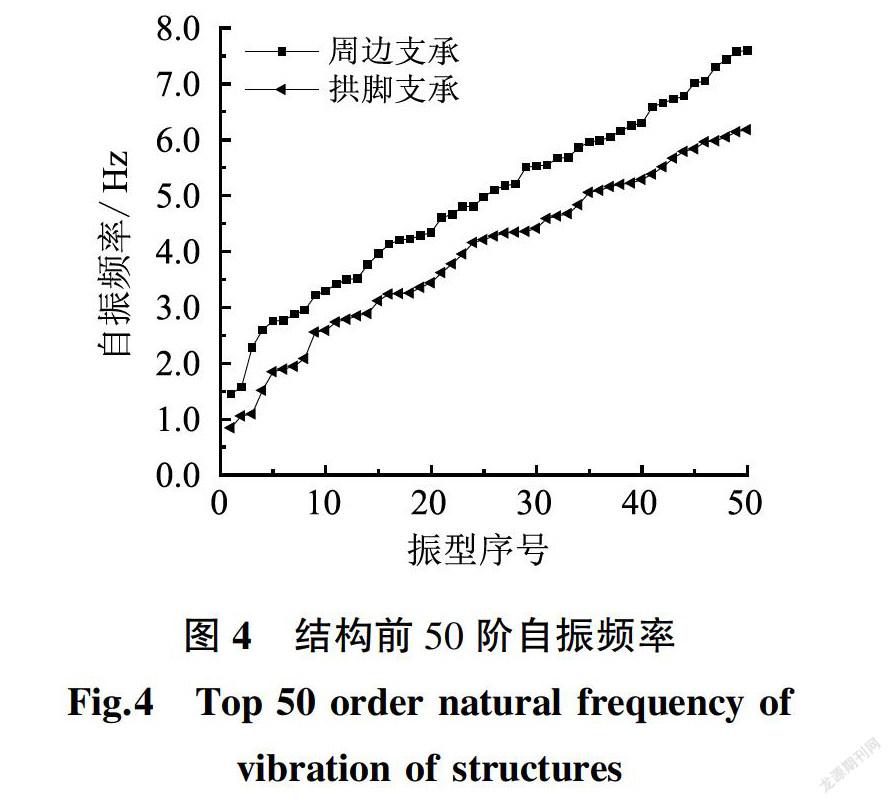
取结构的矢高为f=4.2 m，矢跨比为1/5，将每个密肋平板的拱向均划分为4格，屋面板厚为60 mm，各构件的截面尺寸：主拱和端隔上弦为0.3 m×0.5 m、斜向肋为0.25 m×0.25 m、边梁为0.4 m×0.6 m、脊线为0.3 m×0.50 m。通过有限元法分析结构的自振频率。周边支承和拱脚支承屋盖的前50阶频率结果如图4所示，其中结构前10阶自振频率如表1所示。

由图4可得两种算例的频率分布都较为密集，结构自振频率均具有明显的跳跃性，两种情况下屋盖低频数值较为接近，在屋盖频率阶数较高时，这两者之间频率差开始增大，且周边支承屋盖各阶频率明显大于拱脚支承屋盖，表明周边支承对屋盖刚度的影响比较明显。

2.2 振型

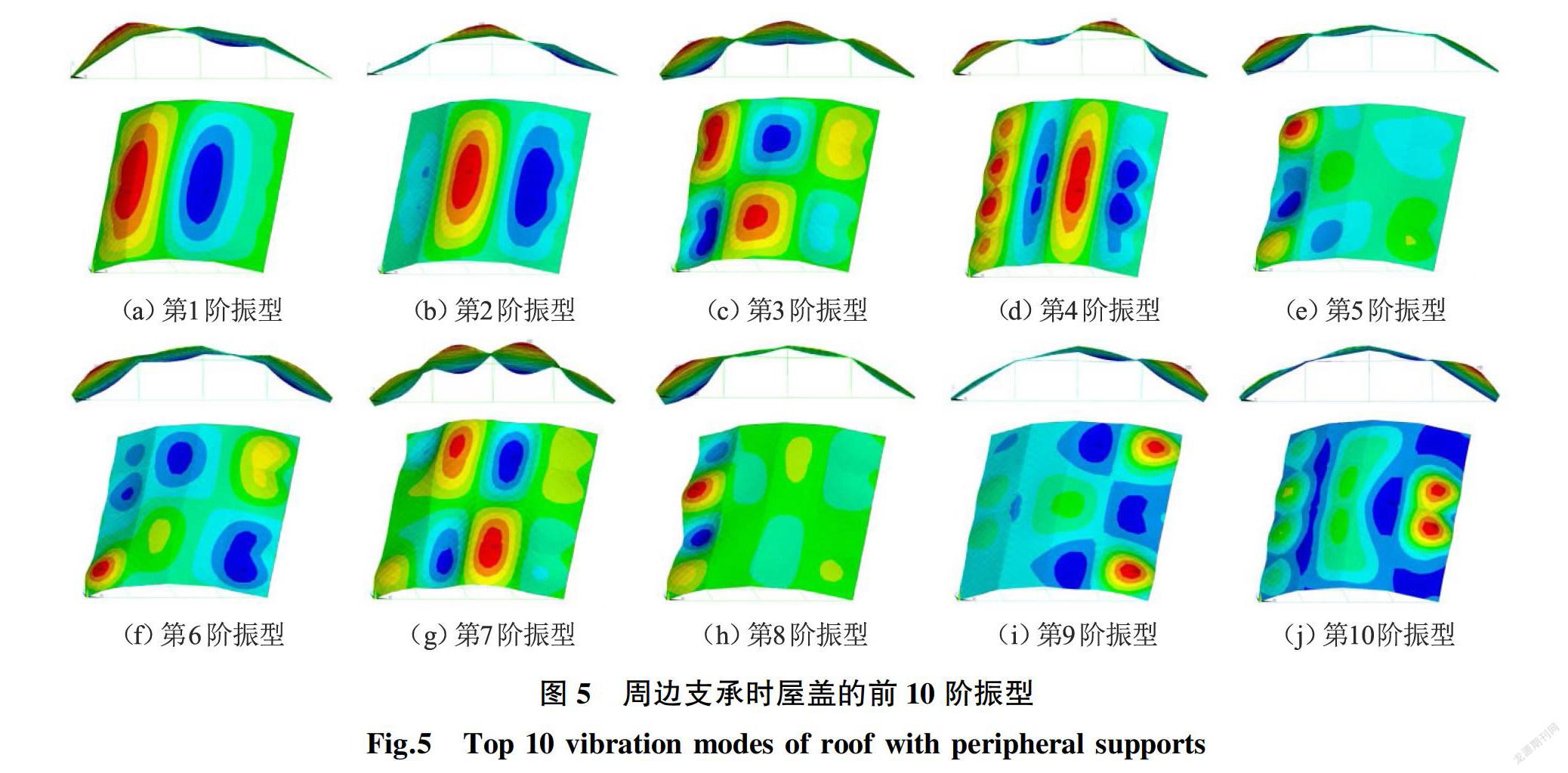
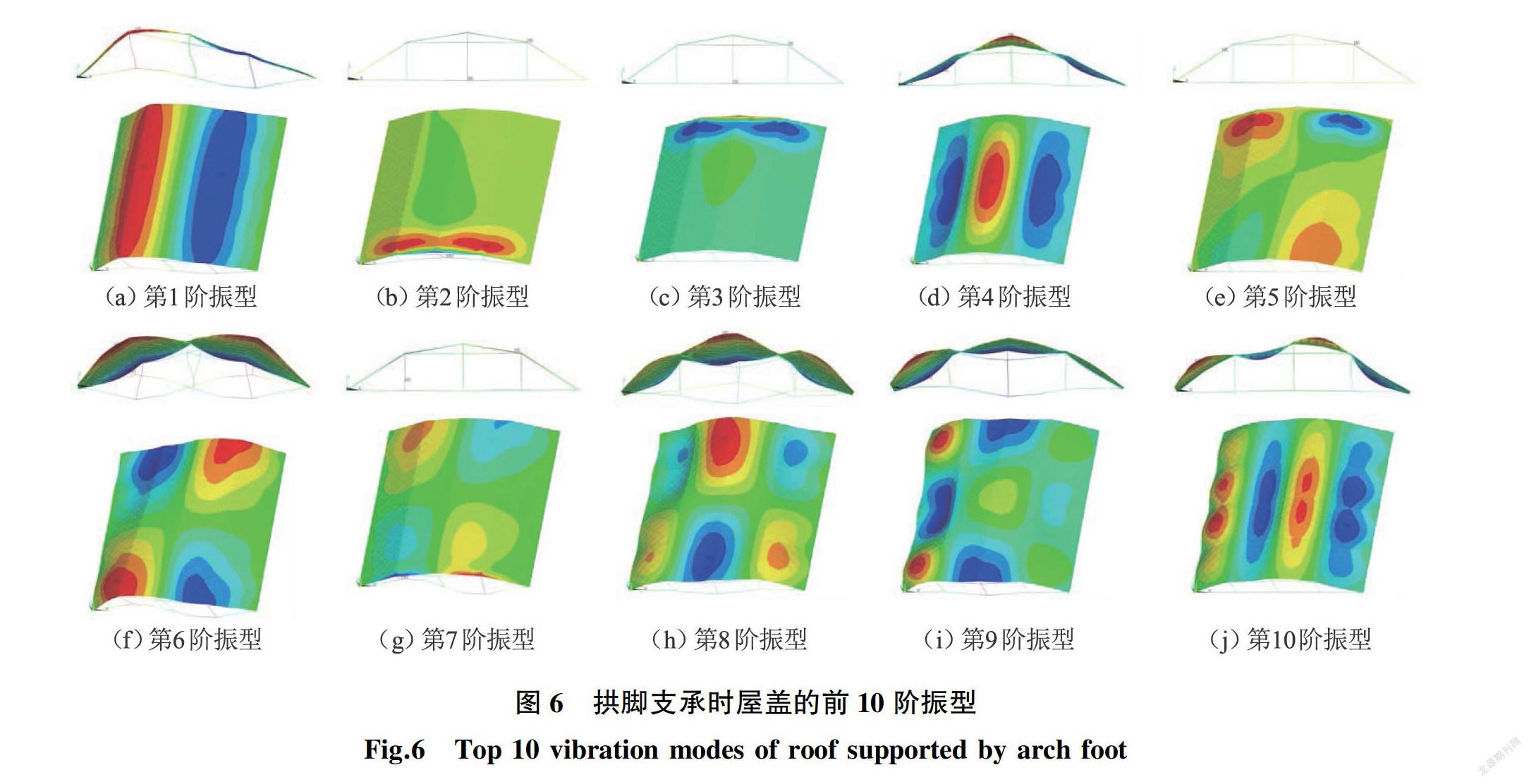
经过有限元分析可得周边支承和拱脚支承屋盖的前10阶振型，分别如图5和图6所示。

周边支承的屋盖结构第1阶振型是关于屋盖中脊线的反对称半波振动;第2阶振型为以脊线为振动节线的屋盖全波正对称振动;第3阶振型为全波正对称振动在主拱两侧呈反向对称状态;第4阶振型是以脊线为振动节线的屋盖竖向全波反对称振动;第5阶振型为屋盖靠近一侧边梁的振动且以主拱为振动节线，第6阶振型为屋盖关于中脊线的不规则反对称半波振动且关于中主拱线两侧呈反对称状态;第7阶振型为以中主拱线为振动节线的屋盖竖向全波反对称振动;第8至10阶振型为以主拱和脊线梁为振动节线多波振动。对于拱脚支承的屋盖，第1阶振型为屋盖关于中脊线的反对称半波振动;第2到3阶振型主要以屋盖山墙处框架的y向水平振动为主;第4阶振型为屋盖的全波正对称振动;第5到7阶振型主要为屋盖的扭转振动;第8阶振型以后多为屋盖竖向多波振动。

由以上分析可知，较多振型幅度最大值出现在屋盖两端山墙处，并且拱脚支承时屋盖的第5到第7阶振型中出现了明显的扭转振动，其前10阶振型如图6所示，因此应当考虑山墙空腹桁架对屋盖抗震时的有利作用。

3 屋盖自振频率的参数化分析

3.1 屋盖矢跨比对自振频率的影响

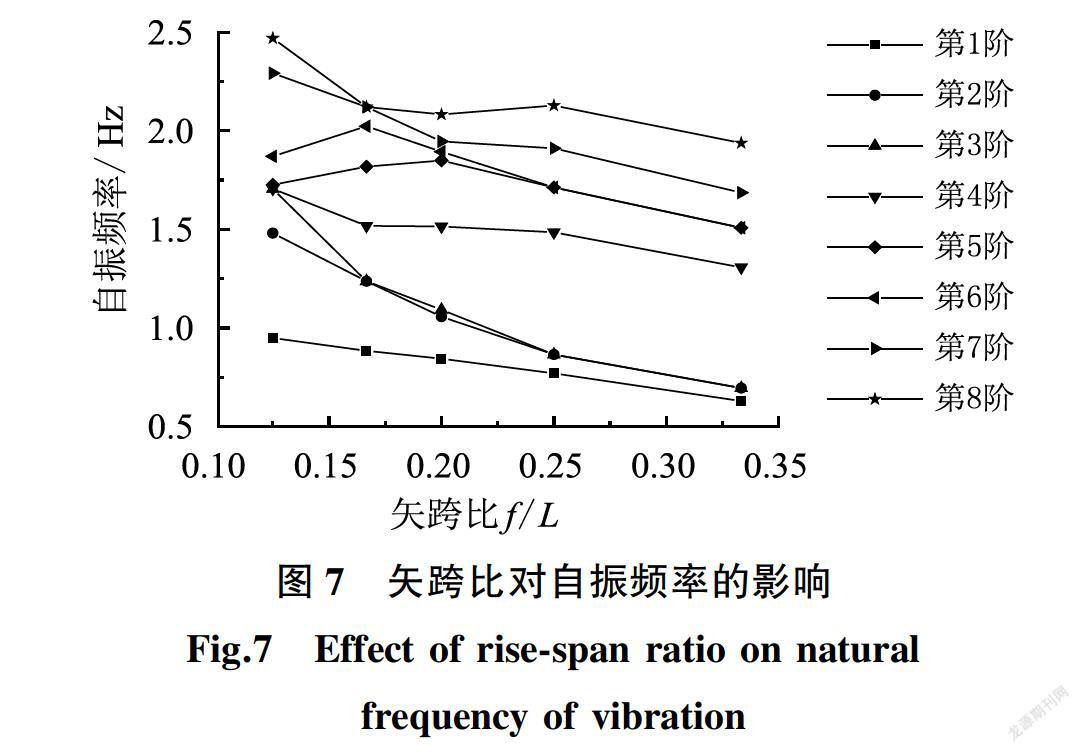
基于基本算例，仅改变屋盖矢跨比进行了5个算例计算，矢跨比分别为1/3、1/4、1/5、1/6和1/8。屋盖的前8阶自振频率结果如图7所示。

由图7可得出屋盖结构前两阶自振频率随着矢跨比的增加而减小;第3阶矢跨比在小于1/6之前有所下降，在1/6后其梯度放缓，在1/4之后其梯度再次减缓;第4阶频率随矢跨比的增加而降低，在1/6与1/4之间减小速率放缓，但在1/4后频率的减缓速率再次增大;第5阶频率在矢跨比低于1/5处于上升阶段并在1/5处达到极大值之后处于下降阶段;第6阶频率在矢跨比低于1/6处于上升阶段并在1/6处达到极大值之后处于下降阶段;第7阶频率总体趋势是下降的，当矢跨比在1/5到1/4区间内下降有所减缓;第8阶频率随着矢跨比的增大总体来说是减小的，但在矢跨比1/5到1/4时出现略微上升，并在1/4处取得最大值，之后呈现下降走势。可知自振频率的趋势随着矢跨比增大而下降的。

对屋盖结构基频而言，随着矢跨比的增加，基频有着近似线性减小的趋势，矢跨比f/L=1/8时，基频为0.948 8 Hz。矢跨比为1/3时，基频为0629 2 Hz，减小了约33.7%，因此过高的矢跨比并不能提高结构的整体刚度，这是因为矢跨比的增加会增加屋盖的展开面积进而增加结构的自重，而在此时屋盖网格划分数不变会降低密肋屋盖板的刚度;同时屋盖的矢跨比过高时将降低屋盖结构山墙框架处的面外刚度，以影响山墙框架对屋盖的约束作用，建议屋盖的矢跨比取1/6～1/4。

3.2 斜向肋刚度对自振频率的影响

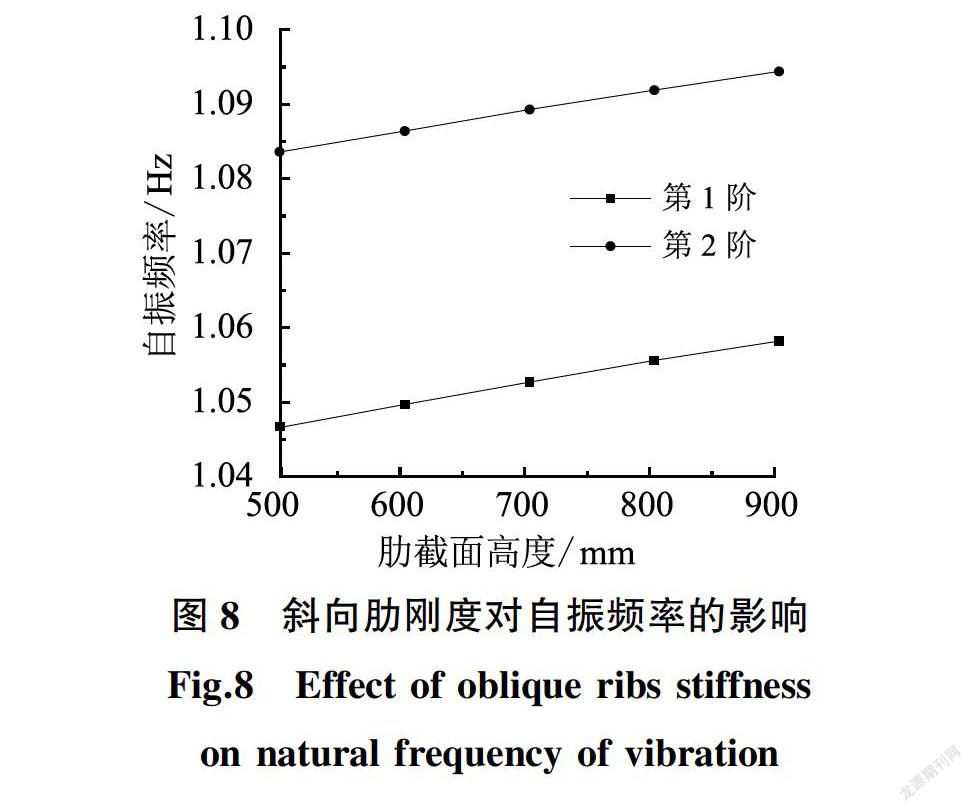
为分析斜向肋梁的刚度变化对屋盖自振频率的影响，计算5个算例，取斜肋梁截面高度分别为0.5 m、0.6 m、0.7 m、0.8 m和0.9 m，结构基频随斜肋刚度变化的结果如图8所示。

屋盖结构的第1、2阶自振频率随斜向肋截面高度的增大而线性增大。取斜向密肋梁的横截面高度为0.5 m时，屋盖的竖向振动的基频为1046 7 Hz，而屋盖的y向水平振动的基频为1.084 0 Hz。而斜向肋梁的横截面高度增加到0.9 m时，屋盖竖向振动的基频为1.058 2 Hz，此时屋盖的y向水平振动的基频为1.095 0 Hz。屋盖竖向振动基频由1.046 7 Hz增至1.058 2 Hz，增加了1.1%，增加幅度较小。屋盖的y向水平自振基频从1.084 0 Hz增大至1.095 0 Hz，增大幅度为1.01%。可见斜向肋截面高度的增加虽然可以提高屋盖的自身刚度，但由于斜向密肋梁高度的增大会增加屋盖的自重这一点削弱了密肋梁高度增加对屋盖刚度增大的效果。

综上，斜向肋刚度的增加对屋盖整体刚度的影响不太明显，建议斜向肋高度按屋盖跨度的1/60Symbol～A@

1/45确定。

3.3 脊线刚度对自振频率的影响

基于基本算例讨论脊线刚度的变化对整体结构自振频率的影响，固定主拱截面高度为1.1 m，取主拱截面宽度均为0.4 m。脊线截面宽度均为025 m，其截面高度分别为0.55 m、0.65 m、0.75 m、0.85 m、0.95 m和1.05 m，为屋盖跨度的1/66Symbol～A@

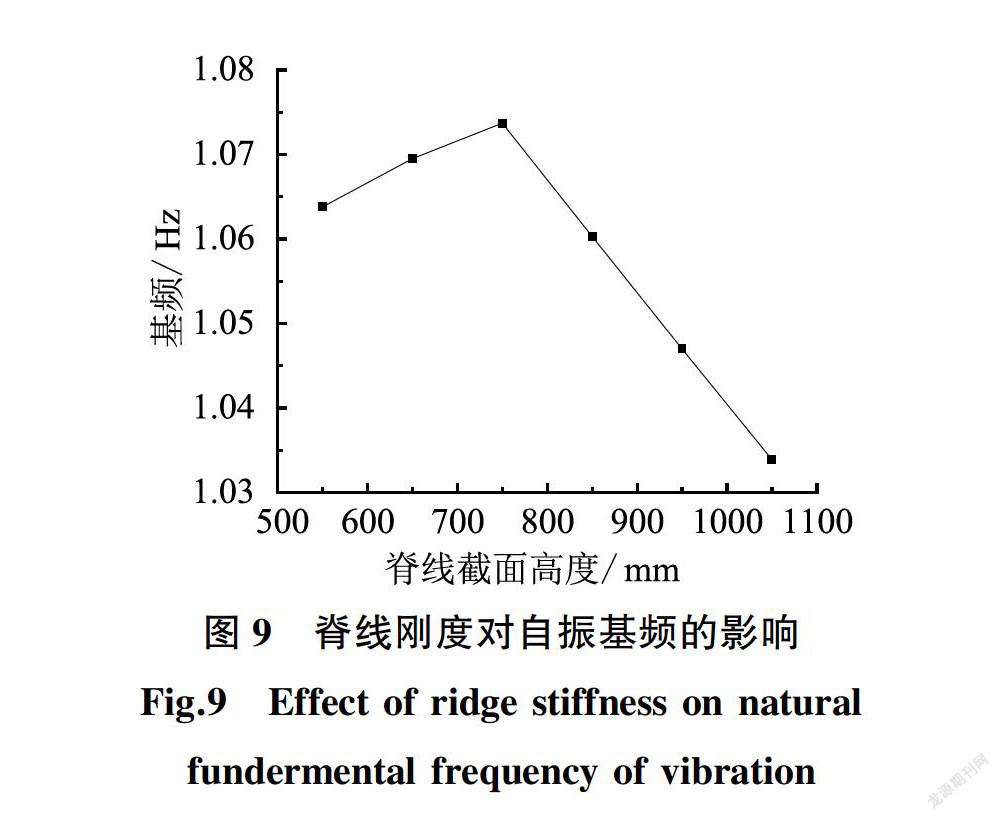
1/34，计算结果如图9所示。

当脊线的横截面高度为0.55 m时，屋盖自由振动基频为1.063 8  Hz;当脊线梁的横向截面高度

为1.05 m时，结构的自振基频为1.034 0 Hz。基频的变化较小，为2.9%，这主要是由于脊线梁在屋盖中所起作用类似于拱向肋侧向系杆的缘故，并且脊线梁高度的增大会增加屋盖的自重这一点减弱了脊线梁高度增加对屋盖整体刚度增大的效果。综上分析，已知结构的第一阶自振频率反映结构刚度，可见脊线梁刚度基本不影响整体结构刚度，建议脊线梁横向截面高度可按实际工程中构造要求确定。

3.4 主拱刚度对自振频率的影响

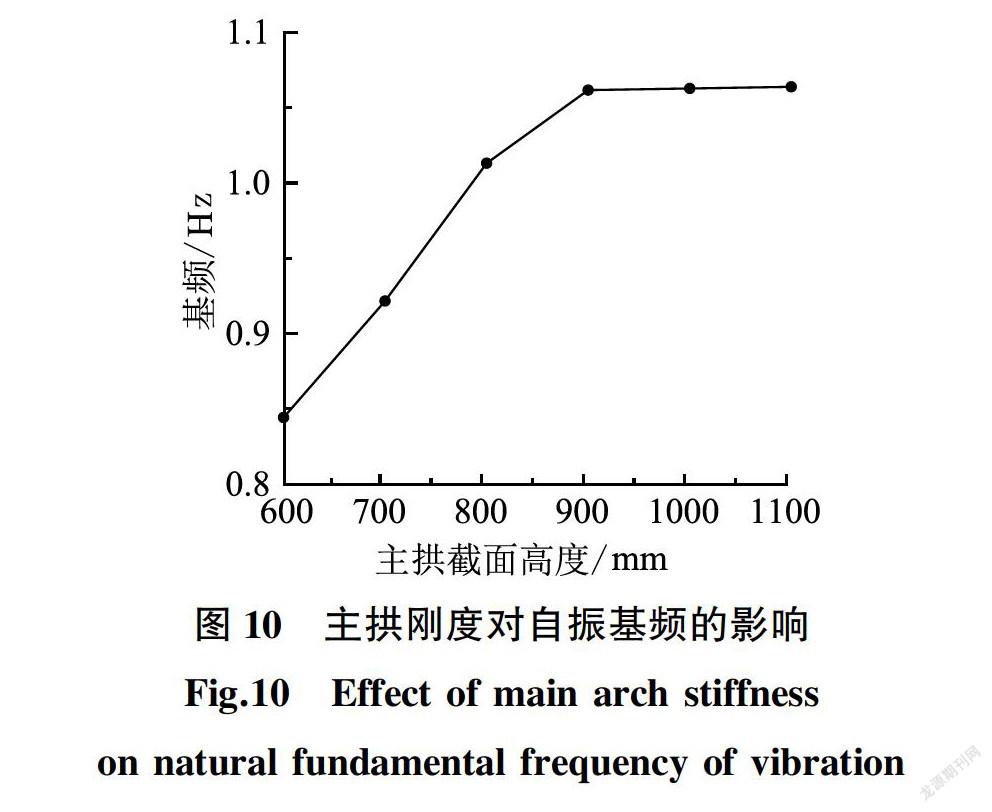
为分析主拱刚度对屋盖动力特性的影响，仅改变结构中主拱横截面高度分析6个案例，其剖面横向截面高度如下：0.6 m、0.7 m、0.8 m、0.9 m、10 m和1.1 m。其自振基频有限元结果如图10所示。

拱肋梁的横截面高度为0.6 m时，屋盖的基频为0.844 2 Hz，而其横截面高度为11 m时，屋盖的基频为1.063 8 Hz，增大了260%。可

见主拱向肋横截面高度的增加可以明显提高屋盖的整体刚度。不过随着主拱肋梁截面高度的增大，会

使结构的自重也随之增加，也会削弱主拱向肋梁的刚度增大对基频的影响，并且不利于屋盖的抗震。综合考虑下，建议主拱肋梁的横截面高度按屋盖拱向跨度的1/51Symbol～A@

1/40确定。

3.5 边梁刚度对自振频率的影响

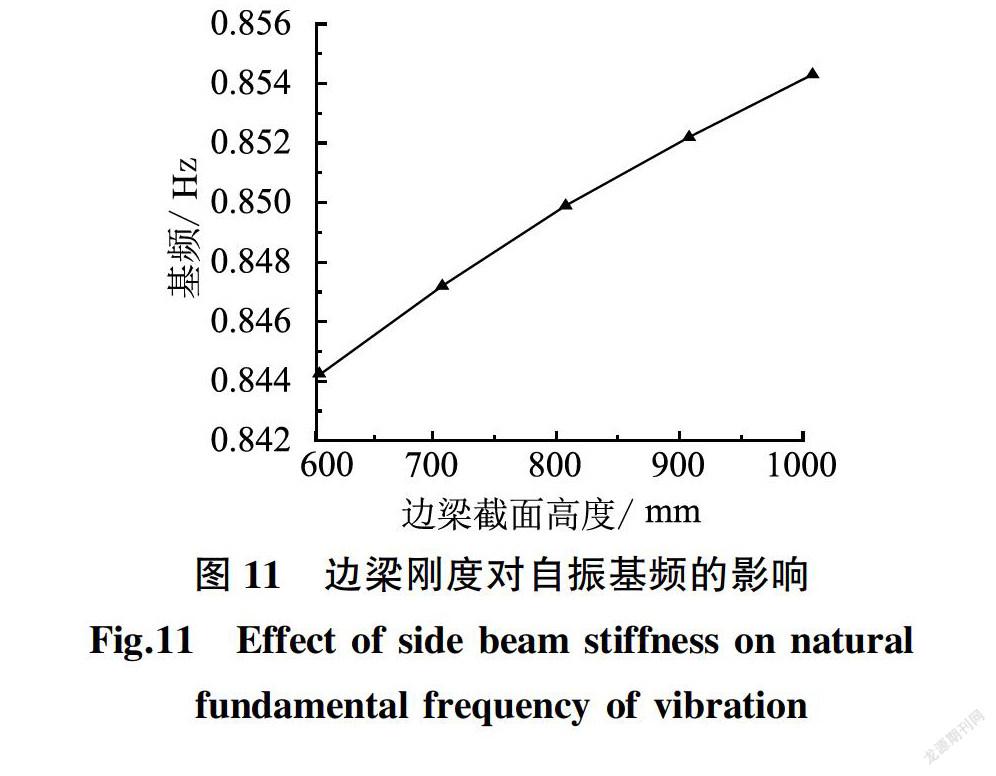
结构在点支承时边梁是重要传力构件，且以受弯为主，这里取边梁的截面宽度b为0.4 m，仅改变边梁的截面高度hL计算5个算例，且hL按级差0.1 m由0.6 m增大至1.0 m，以考察边梁刚度的变化对屋盖结构自振特性的影响，其有限元分析结果如图11所示。

当边梁截面高度为0.6 m时，屋盖基频为0844 0 Hz，而将边梁截面高度增至1.0 m时，基频为0854 0 Hz，增大了1.2%。可得边梁横截面抗弯刚度不能有效提高自身整体刚度。究其原因，边梁承受主拱传来的弯矩使得边梁截面受扭，而矩形边梁在抗扭时发生转动的主要控制因素是截面宽度，且考虑边梁自重将影响结构的内力变化，因此取边梁跨度的1/20Symbol～A@

1/15为边梁的截面高度。

3.6 下部支座共同工作对屋盖自振频率的影响

3.6.1 三角形支座对屋盖自振频率的影响

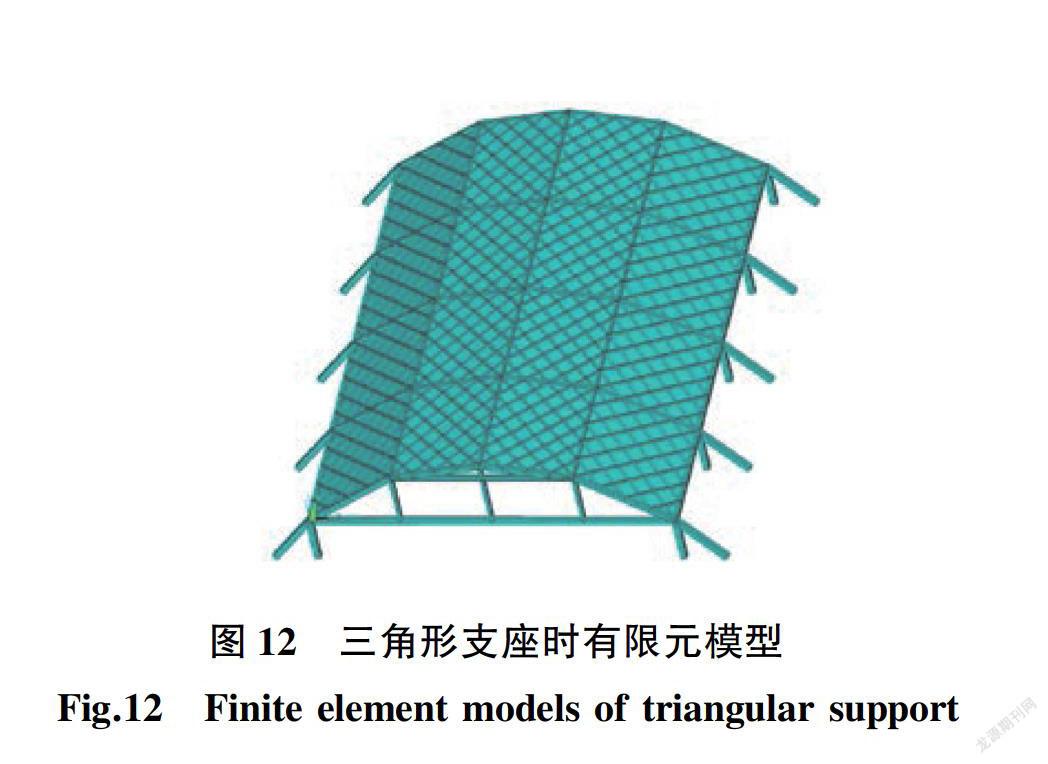
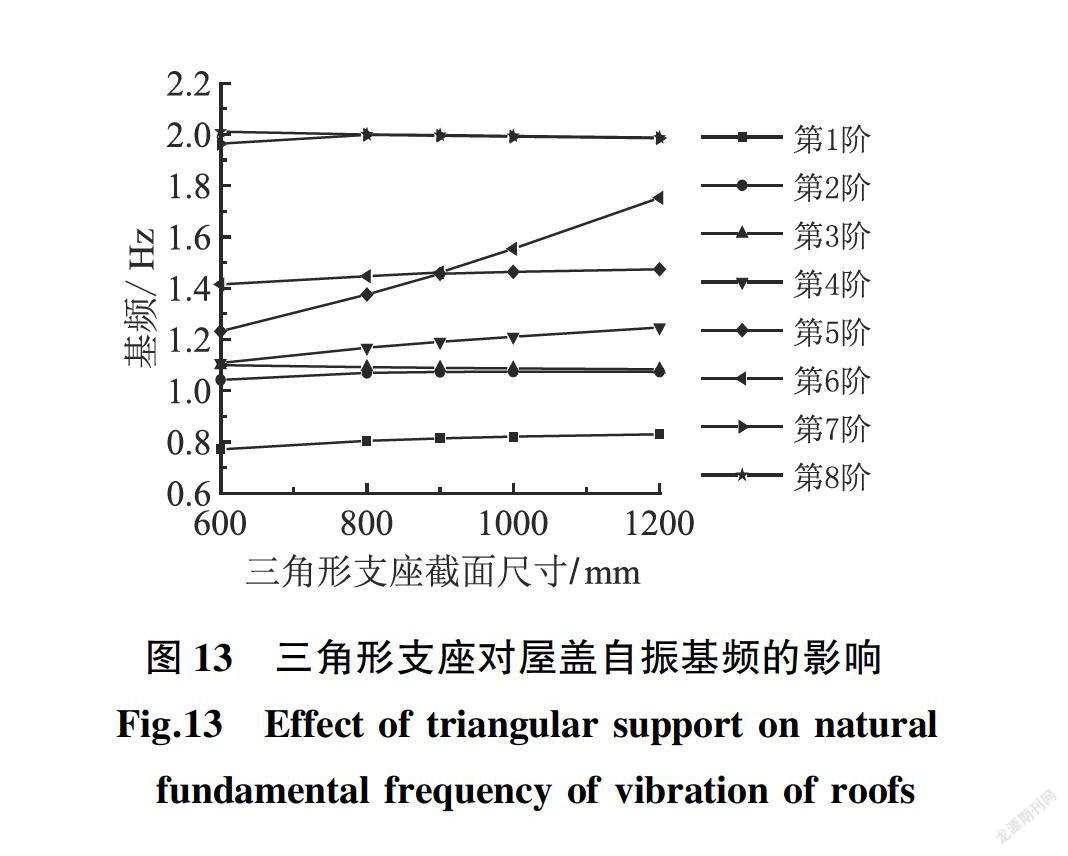
现考虑一种三角形抗推支座约束对屋盖自振频率的影响，以期为今后的工程实践提供参考。拱形屋盖产生的推力需要下部结构平衡，考虑推力比上例（3.1节）更大的情况下可以采用三角形支座对上部屋盖支承，在有限元建模时，三角形支座设为梁单元，三角形支座由两个方柱组成，其有限元模型如图12所示。本文在基本算例基础上，将三角形支座方柱的边长由0.6 m按0.1 m逐级增大至1.1 m，以考察协同工作时三角形支座对结构自振频率的影响，三角形支座抗推刚度对屋盖自振频率的分析如图13所示。

由图13可知，随着三角形支座截面高度的增大，结构基频近似按线性增长。当方柱截面边长为0.6 m时，结构屋盖竖向振动的基频为2.712 0 Hz，沿y向水平振动的基频为2.987 6 Hz，结构以扭转振动为主的基频为4.829 0 Hz;而方柱截面边长变为1.1 m时，屋盖结构以竖向振动为主的基频为2.934 0 Hz，而y向的水平振动的基频为3.200 0 Hz，以扭转振动为主的基频为5.772 0 Hz。基频分别增大约82%、7.1%和19.5%，可见提高三角形支座截面尺寸是有利于提高结构整体刚度的，并对整理结构扭转振动的约束的效果最佳。由有限元分析可知，第1、第3、第6和第8阶振型为屋盖的的竖向振动，振动随振型的推移有往屋盖两端支座处发展的趋势，因此需要考虑边梁对屋盖约束的影响;第2、第4和第5阶振型为整体结构沿x向平向振动，并伴随端隔空腹桁架的y向水平振动;第7阶振型为屋盖的整体扭转振动，此时屋盖左右脊线处振动幅度最大，需要考虑脊线对屋盖自振频率影响。

3.6.2 周边支承对屋盖自振频率的影响

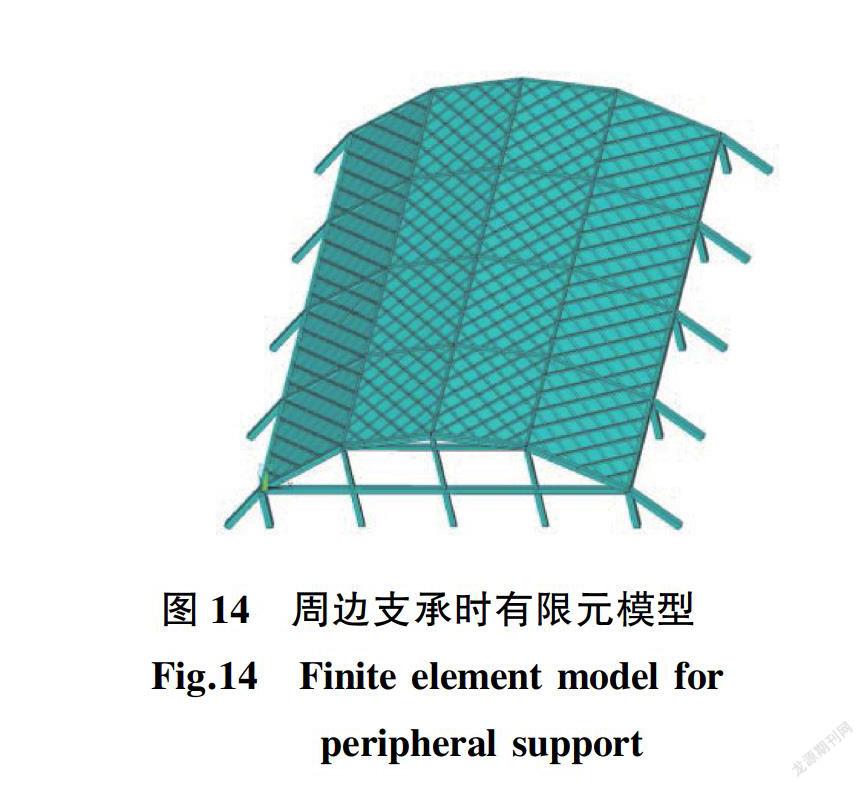
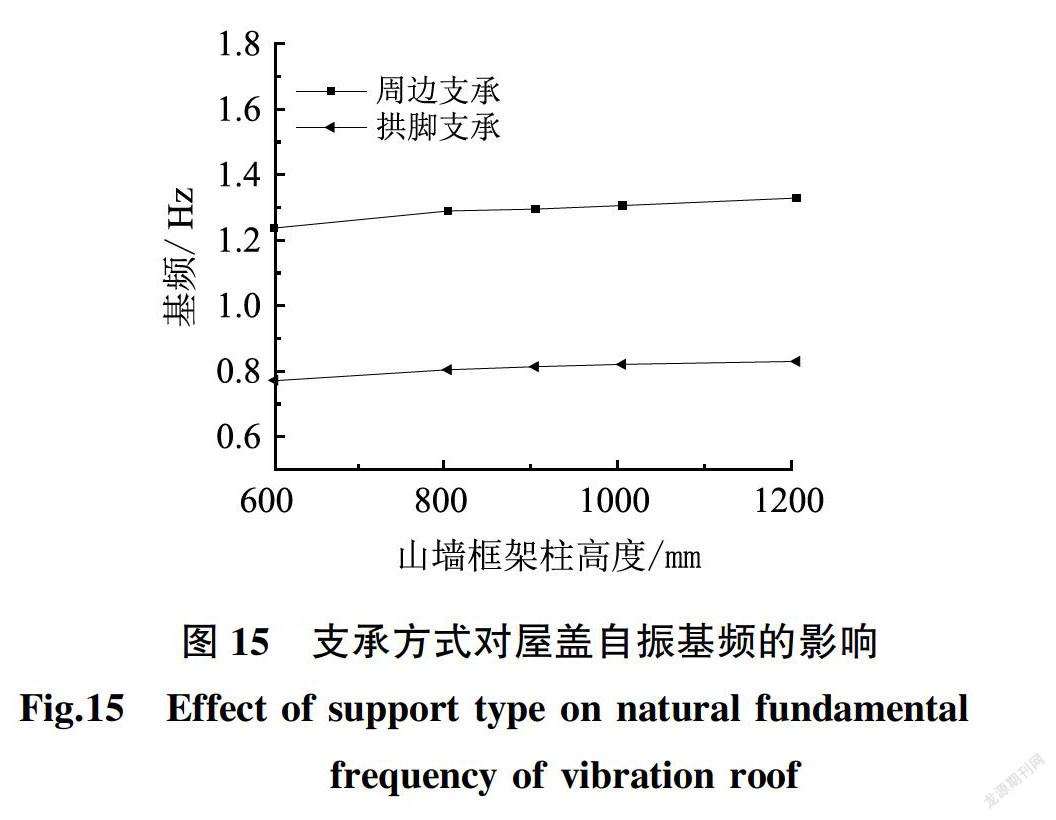
基于上节分析，本课题主要是想利用斜放网格使脊线更大程度参与结构受力，但经脊线参数化分析可知效果并不理想，现将图12结构中脊线两侧山墙空腹桁架腹杆往下延伸，其有限元模型如图14所示。山墙框架柱的尺寸和三角形支座柱保持一致，并在山墻框架柱底节点采取约束结点的所有位移即视为固定约束端，此时支承方式变为周边支承。取柱截面高度为0.6 m、0.8 m、0.9 m、1.0 m和1.2 m五个算例进行自振基频对比分析，计算结果如图15所示。

从图15可得，当山墙框架柱横向截面高度为0.6 m时，周边支承屋盖的自振基频为1.237 0 Hz，而拱脚支承的屋盖仅有0.771 0 Hz，增大了60.4%，当柱截面高度为1.2 m时，周边支承屋盖的基频为1329 0 Hz，拱脚支承屋盖仅有0.830 0 Hz，增大了60.1%。由以上分析可得，在整体结构下考虑山墙框架的支承相当于给屋盖施加了周边约束，使屋盖的各个构件更有效的受力。综上，脊线约束对含下部抗推支座的整体结构提高刚度的效果良好。

3.7 屋面板厚度对自振频率的影响

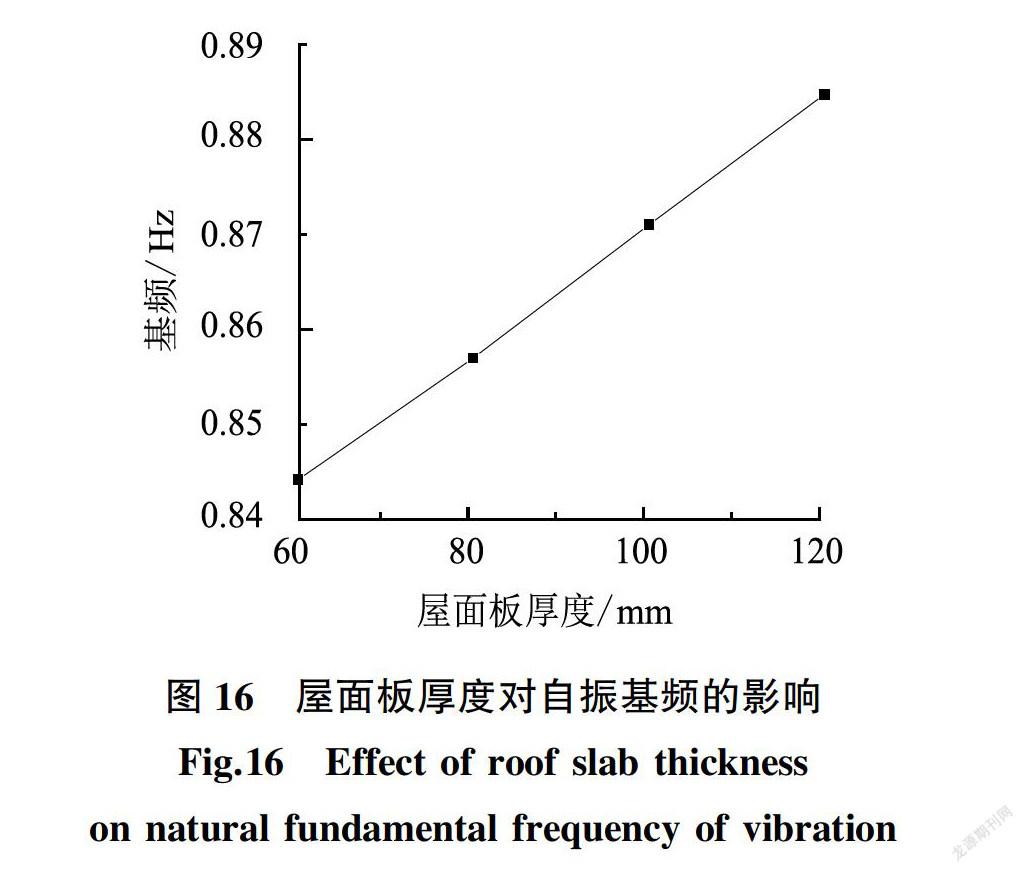
在自振特性分析算例的基础上仅改变屋面板厚来计算5个算例，板厚分別为60 mm、80 mm、100 mm和120 mm，以此来讨论屋面板厚度的变化对屋盖结构自振特性的影响，其分析结果如图16所示。

当屋面板厚度为60 mm时，屋盖的自振基频为0.844 0 Hz，当主拱肋梁截面高度为120 mm时，屋盖的自振基频为0.885 0 Hz，增大了4.9%。可见屋面板厚度可略微提高屋盖自身刚度。在混凝土结构设计规范中，规定了屋面板最小厚度来保证屋盖结构的安全、可靠性。工程设计中，结构屋面板厚度增大会增大结构的自重，这会对结构的抗震带来不利影响。在满足结构正常使用承载力的要求下，屋面板厚度不宜过大，建议屋面板在满足使用条件的情况下一般取80 mm或90 mm即可。

4 结论

（1）在两种不同支承方式下结构频率分布都较为密集，结构自振频率均具有明显的跳跃性。且周边支承屋盖的各阶频率明显大于拱脚支承的屋盖，结合两者的振型图表明考虑周边支承对屋盖整体刚度的提高较大。

（2）矢跨比对屋盖结构基频影响较小，较大的矢跨比会减弱山墙框架的面外刚度，建议屋盖的矢跨比取1/6～1/4。

（3）斜向肋梁是整个屋盖结构中主要的传力构件之一，提高斜向肋梁的横截面刚度有利于提高屋盖整体刚度，提高结构抗震能力，建议斜向密肋梁的横截面高度按屋盖拱向跨度的1/60Symbol～A@

1/45确定。

（4）脊线梁的横截面刚度在屋盖的整体刚度中的贡献较小，建议脊线梁的横截面高度按构造确定;结构的基频随边梁高度的增加近似呈线性增大但增幅不大，取边梁跨度的1/20Symbol～A@

1/15为边梁横截面高度;主拱刚度在屋盖整体刚度贡献较大，建议主拱梁的横截面高度可取屋盖跨度的1/51Symbol～A@

1/40。

（5）提高结构的支座抗推刚度有利于提高结构整体刚度。采用三角形抗推支座约束屋盖时，对整体结构抗扭刚度的提升最大;并且周边支承对提高整体结构刚度的效果良好。

（6）屋面板作为结构的刚度储备，在满足混凝土设计规范的标准下不应取值过大，建议屋面板厚在满足使用条件后不宜取值太厚。

参考文献：

[1]董石麟，罗尧治，赵阳.大跨空间结构的工程实践与学科发展[J].空间结构，2005，11（4）：3-10.

[2]LUU  C H，MO Y  L，HSU T  T  C.Development of CSMM￣based shell element for reinforced concrete structures[J].Engineering Structures，2017，132：778-790.

[3]DIEDERIK V，PHILIPPE B.Design process for prototype concrete shells using a hybrid cable-net and fabric formwork[J].Engineering Structures，2014，75：39-50.

[4]崔昌禹，崔国勇，姜宝石.自由曲面混凝土壳体结构静力试验研究[J].建筑结构学报，2014，35（11）：77-84.

[5]SHAREI E，SCHOLZEN  A，HEGGER J，et al.Structural behavior of a lightweight，textile-reinforced concrete barrel vault shell.Composite Structures，2017，171：505-514.

[6]VERWIMP E，TYSMANS T，MOLLAERT M，et al.Experimental and numerical buckling analysis of a thin TRC dome[J].Thin￣Walled Structures，2015，94：89-97.

[7]董石麟，罗尧治，赵阳.新型空间结构分析、设计与施工[M].北京：人民交通出版社，2006.

[8]殷志祥. 双层柱面组合网壳结构极限承载力分析[C]//天津大学建筑工程学院.第三届全国现代结构工程学术研讨会论文集，天津：天津大学建筑工程学院，全国现代结构工程学术研讨会学术委员会，2003：532-535.

[9]严慧，王勇.新型穹顶混合风壳的理论分析和受力特性研究[C]//中国建筑科学研究院建筑结构研究所.第九届空间结构学术会议论文集，萧山：中国土木工程学会桥梁及结构工程分会空间结构委员会，2000：218-223.

[10]孔煜，代富红，严标.混合型网壳结构的有限元法分析及受力特性的研究[J].贵州工业大学学报（自然科学版），2002，31（5）：81-85.

[11]常玉珍，吴敏哲.组合肋壳结构静力特性分析[J].建筑结构，2009，39（4）：54-56.

[12]WONG H T，TENG J G.Buckling behaviour of model steel base shells of the Comshell roof system.Journal of Constructional Steel Research.2006，62（1/2）：4-19.

[13]邓毅强，邹银生，王汉珽.大跨度钢-混凝土组合薄壳屋盖模型试验研究[J].空间结构，2006，12（1）：12-17.

[14]张华刚，马克俭，杨期柱.混凝土大跨度密肋式折板壳的结构形式与分类[J].贵州工业大学学报（自然科学版），2008，37（4）：55-59.

[15]張华刚，杨期柱，马克俭，等.人字形密肋式折板拱壳的静力性能分析及其工程应用[J].建筑结构学报，2009，30（s2）：29-35.

[16] 齐卫东，张华刚，方强，等.混凝土人字形密肋网壳与下部结构共同工作性能分析[J].空间结构，2017，32（4）：36-44.

[17] 齐卫东，张华刚，方强，等.混凝土人字形密肋网壳与下部结构共同工作动力特性分析[J].贵州大学学报（自然科学版），2017，34（1）：83-89.

[18]方强，张华刚，齐卫东，等.混凝土幕形密肋网壳的静力性能及参数化分析[J].广西大学学报（自然科学版），2017，42（4）：1307-1316.

[19]方强，张华刚，齐卫东，等.混凝土折板式密肋拟扁壳的静力性能分析[J].建筑科学，2017，33（11）：25-31.

[20]方强，张华刚，齐卫东，等.混凝土折板式拟扁网壳的自振特性参数分析[J].贵州大学学报（自然科学版），2016，33（5）：102-106，125.

[21]柳勇斌，张华刚，宋勇，等.混凝土人字形折板式网壳结构的弹性稳定分析[J].贵州大学学报（自然科学版），2018，32（4）：100-105.

（责任编辑：周晓南）

Dynamic Characteristics and Parametric Analysis of Ribbed

Reticulated Shells with Inclined Grid Cylindrical Surfaces

ZHU Rui1，2，ZHANG Huagang1*，CHEN Shouyan1，JIANG Lan1，3，TANG Zanhui1

（1.Space Structures Research Center，Guizhou University，Guiyang  550003，China;2. Department of Architecture and

Environmental  Engineering， Guangdong Institute of Water Resources and Electric Power， Guangzhou  510635， China;

3.School of Civil Engineering，Hunan University，Changsha 410012，China）

Abstract：

To understand the quasi diagonal grid concrete ribbed cylindrical shell flap dynamic characteristics mesh， 39 examples were calculated using the finite element method.The natural vibration frequencies and modes of the surrounding supporting and arch supporting roofs were compared. Through the finite element parametric analysis， the influences of the ratio of beam to span， bearing constraints， oblique multi￣ribbed beam stiffness， ridge beam stiffness， main arch beam stiffness， side beam stiffness and roof plate thickness on the natural vibration frequency of the structure were investigated. The results show that：In consideration of constraints on the overall configuration of the ridgeline to enhance the overall stiffness larger roof; vector roof span less than the effect on the fundamental frequency of vibration， large span ratio will weaken the stiffness of the outer surface of the end compartment， recommendations span ratio takes 1/6 to 1/4; abutment constraint greatly enhance the overall stiffness of the roof; oblique ribs increase the stiffness improve the overall stiffness of the roof， it is recommended to take an oblique section height of the ribs of a roof span 1/60～1/45; ridgeline section stiffness in the overall stiffness of the roof beam of a small contribution， recommended cross￣sectional height of the ridge line is determined by the configuration; main arch stiffness contributed greatly to the overall stiffness of the roof， the main arch recommendations section height taken roof span 1/51～1/40; The side beam stiffness has little contribution to the overall structure， and the 1/20～1/15 of the side beam span is the height of the side beam; roof storage structure as rigidity meet the criteria the value should not be too large in the case.

Key words：

concrete; inclined grid folded￣plated ribbed shell; bearing constraints; joint work; dynamic characteristics; parametric analysis