一种改进的Apriori算法在精准扶贫中的应用研究

何庆 刘亮

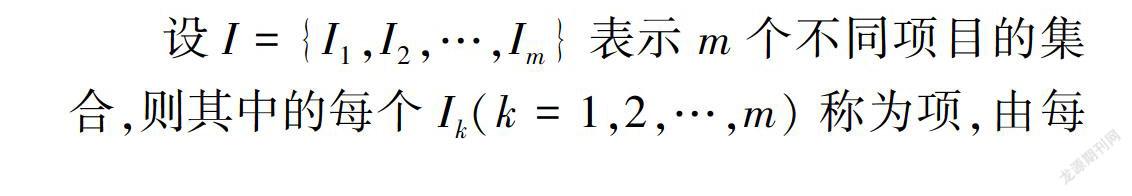
摘 要：随着精准扶贫建档立卡工作的实施，精准扶贫系统已积累了大量数据，利用高效的关联规则算法挖掘其中隐含的有用信息对助力精准扶贫工作具有重要意义。本文针对贫困户建档立卡数据的数据重复率高，属性多样特点，提出一种改进的Apriori算法，利用对矩阵的数据结构和集合的相关性质来构建候选项集，避免重复扫描数据库以及逐层的剪枝连接运算，提高算法挖掘效率;通过对实际贫困户建档立卡数据进行挖掘，证明了该算法在最小支持度阈值较低的条件下挖掘效率优于传统Apriori算法。

关键词：关联规则; 频繁项集;精准扶贫;Apriori算法

中图分类号：TP301.6

文献标识码： A

近年来，基于互联网的扶贫工作积累了大量的数据，如何有效利用这些数据来推动扶贫工作的开展成为了扶贫部门亟待解决的问题。为帮助真正的贫困人口摆脱贫困，精准扶贫工作需对大量扶贫数据进行深入挖掘，精确瞄准致贫原因[1]。Apriori[2]算法作为关联分析领域最经典的算法，目前许多关联分析算法都是在其基础上演化而来[3-6]，目的是为了解决Apriori算法产生大量候选项集以及多次扫描数据库所造成的算法运行效率问题，此类改进算法对于候选项集的构建大多還是沿用Apriori算法中的连接和剪枝思想，但当事物数据库中的每个事物都包含有较多的数据项且数据项重复率较高时，在最小支持度阈值较低情况下，Apriori算法的连接和剪枝效率就会大大降低[7-8]，从而影响算法挖掘性能。

传统Apriori算法为挖掘最大频繁项集，需进行逐步地剪枝并且需要频繁扫描数据库[9]。为了解决这两个问题，许多学者从不同的角度对Apriori算法进行改进，例如从减少扫描数据库造成的I/O开销的角度，有学者提出了基于矩阵的改进Apriori算法[10-12];文献[10]提出一种基于矩阵和权重的改进算法，利用0￣1矩阵来表示事物数据库，避免对数据库的重复扫描;文献[11]通过增加向量的方式减小矩阵规模，避免多次扫描数据库;文献[12]提出利用事物矩阵和项集矩阵相乘来改进反复扫描数据库的问题，以此来提高算法运行效率。上述算法在挖掘频繁项集过程中，在剪枝效率高的前提下均能获得较高挖掘效率，但当剪枝效果不理想时，为确定不同长度项集的支持度信息而多次处理和扫描矩阵反而会降低算法性能。

在贫困户的建档立卡数据中，同一地区的贫困户由于地理环境、生活习惯、经济发展等因素，通常会具有许多相同的贫困特征，从而导致贫困特征事物数据库具有贫困特征项多且重复率高的特点，传统Apriori算法在处理此类数据库时，挖掘效率较低。针对这一问题，本文将事物数据库转换为矩阵表示的同时，通过计算矩阵行向量所代表集合的交集和子集来构造候选项集，避免逐步的剪枝连接和重复扫描数据库，解决了传统Apriori算法在较低最小支持度阈值条件挖掘效率低的问题。

1 频繁项集挖掘

1.1 基本概念

（1）项与项集

设I={I1，I2，…，Im}表示m个不同项目的集合，则其中的每个Ik（k=1，2，…，m）称为项，由每个Ik（k=1，2，…，m）所构成的集合I则称为项集，集合中所容纳的项的数目则表示该项集的长度，长度为m的项集则称之为m￣项集。

（2）事物与事物数据库

事物T是项集I的子集[13]，即T={T1，T2，…，Tk}，Tk∈I，表示数据库当中记录的集合，常用标识符TID来表示，而所有事物的集合则称为事物数据库，常用D来表示。

（3）项集支持度与最小支持度

设XI为数据项集，k为X在事物数据库D中出现的次数，n为D中所包含的事物的总数，则定义X的支持度（Support）为

Support（X）=kn。（1）

最小支持度（Minimum Support）是指在挖掘关联规则的过程中，要求项集满足的最低支持度阈值，当某项集的支持度值高于该阈值时，定义该项集为频繁项集[14]，否则定义为非频繁项集。

（4）关联规则与置信度

关联规则可表示为：AB，其中AI，BI，A∩B≠，它的含义是，若项集A在某一事物中出现，则在同样事物中一定存在项集B，且把A称作该规则的先决条件，B称为规则的结果，规则AB的置信度（Confidence）定义为：

confidence（AB）=Support（A∪B）Support（A）。（2）

最小置信度[15]（Minimum Confidence）则表示关联规则必须满足的最低置信度值，也即是关联规则的最低可靠性。

1.2 相关性质

性质1 若一个项集为频繁项集，则该项集的全部非空子集都必为频繁项集。

性质2 任何非频繁项集的超集一定是非频繁项集。

性质3 若一个事物中不存在任何的频繁k￣项集，则该事物中也必然没有任何的频繁（k+1）￣项集存在。

性质4 若一个非空集合为另一集合的子集，则他们的交集等于该集合本身。

性质5 若有非空集合A，B，C，D，其中B为A的子集，若A∩C=D，则B∩C∈D。

性质6 若事物中存在的数据项数目为k，则长度大于k的频繁项集不可能存在于当前事物中。

2 算法改进

2.1 Apriori_BOMS算法

（1）假设输入数据库D包含m条记录，记录中所包含的数据项总数为n，则将D转换为m×n阶矩阵，设置最小支持度阈值min_support，根据性质2，将不满足支持度阈值要求的元素所在列删除，得到初始化矩阵以及频繁1￣项集L1;

（2）提取所得矩阵每行不为零的元素所组成的项集（至少包含两个元素，否则舍去），并计算所得项集在矩阵中的支持度，将项集及其支持度信息存储于字典original_dic，其中支持度高于所设阈值的项集则定义为矩阵中的已确定初始频繁项集sure。

（3）由于不同项集可能会产生相同的子集，要确定这些相同子集的支持度，需将其单独提取出来;此外，对于非频繁项集，若其子集为频繁项集，则其子集必然会出现在矩阵的其他行向量当中;综上所述，通过求解（2）中所得项集间的交集（产生的交集至少含有两个元素，否则舍去）来获得初始候选项集，利用性质5，满足条件的项集B则无需求解交集;若相交结果中包含有（2）中已确定的频繁项集，由于其支持度已知，则将其从相交结果中删除。

（4）为获得最终候选项集，在得到初始候选项集后，求解其中所有项集的子集（该子集至少包含两个元素，否则舍去），通过集合的并集运算过滤其中的重复项，若产生的子集已存在于original_dic中，因其支持度信息已由（2）中求得，因此将其从本步骤所得结果中舍去，以此得到一个包含交集结果以及其满足条件的子集的列表not_sure，列表中的集合则可看作为候选项集，通过判断not_sure中的项集与original_dic中的项集是否为包含关系，则可确定not_sure中所有项集的支持度信息，并筛选出频繁项集。

（5）根据步骤（2）得到的初始确定频繁项集sure，求其中各项集的子集（至少包含两个元素），并将其子集集合与not_sure做相交运算，得到的交集再与该项集本身做对称交集运算即可快速得到该项集不存在于not_sure中的子集，该子集必为频繁项集且支持度跟随其本身，无需扫描矩阵即可得到满足条件子集的支持度信息，至此完成所有频繁项集挖掘。

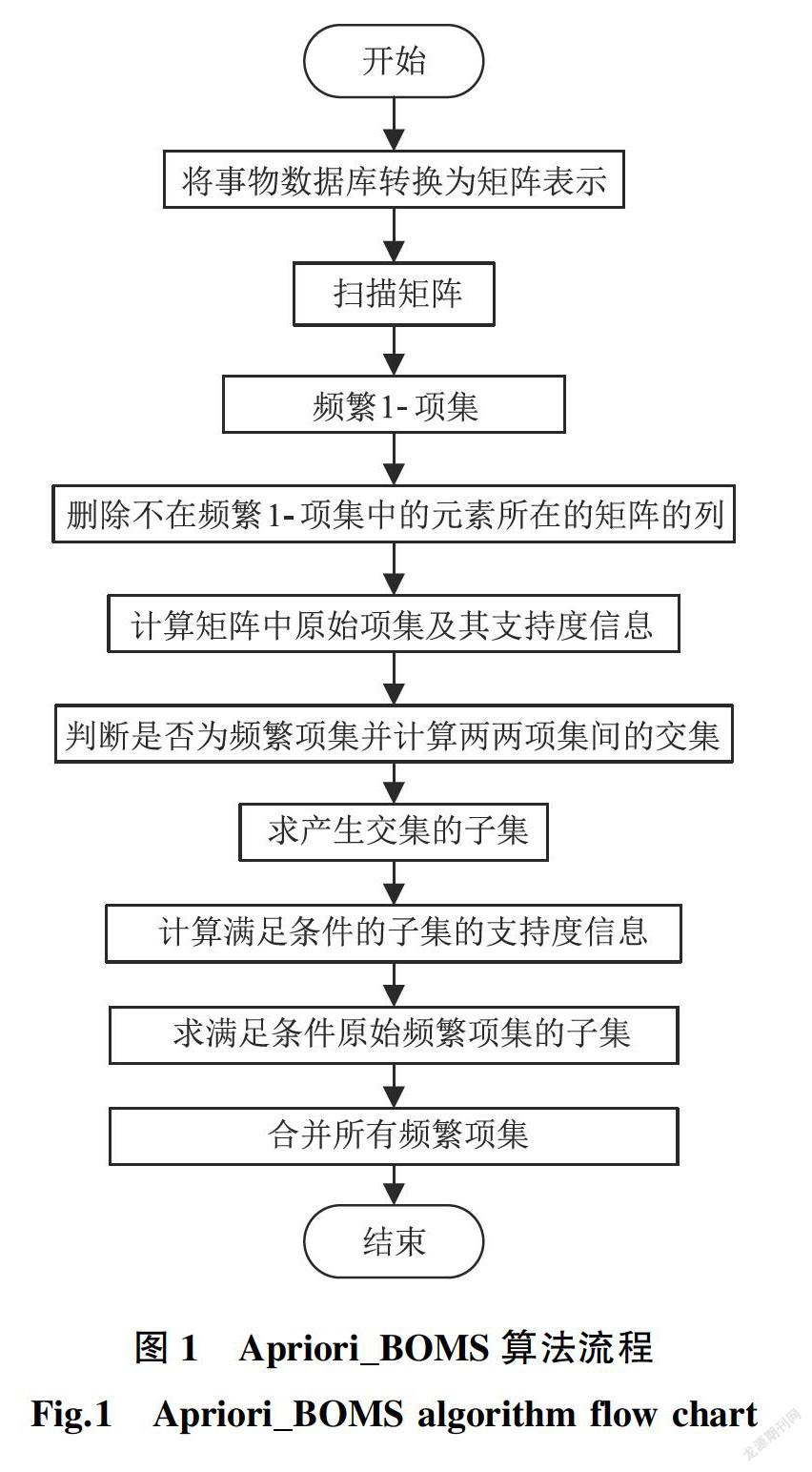
算法流程图如图1所示。

2.2 Apriori_BOMS算法实例

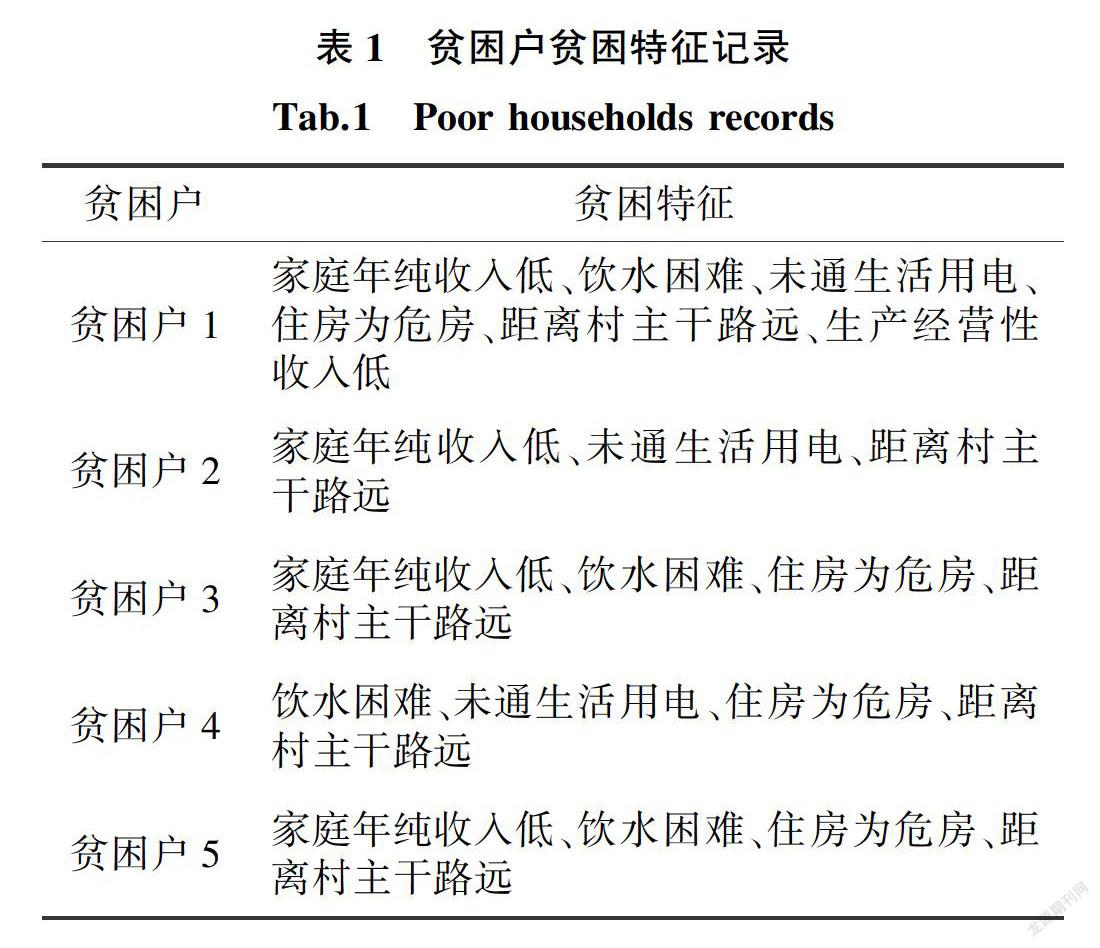
表1为贫困户贫困特征示例数据，其中包含5条贫困户纪录，共6个贫困特征项。

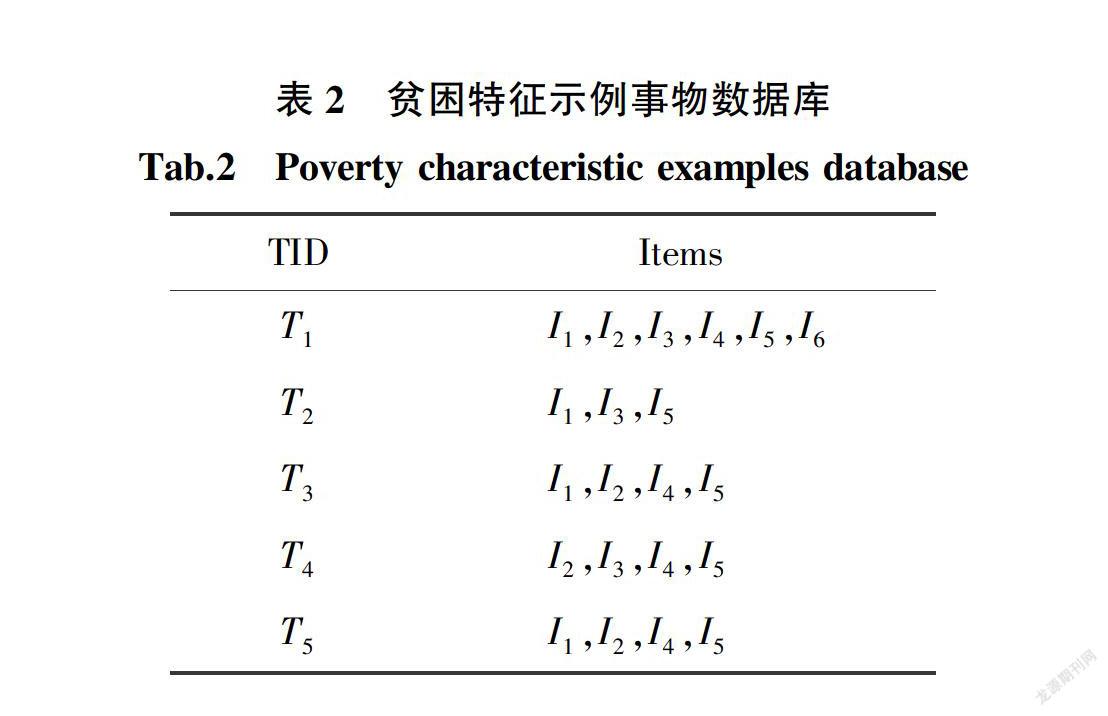
将其中各个贫困特征赋予特定贫困特征标识Ii，每个贫困户对应事物数据库中的一个事物Ti，如表2所示。

设置最小支持度阈值為0.3，根据式（1），因为support（I6）=1/5=0.2<0.3，则将矩阵中低于最小支持度阈值的元素所在列删除得到初始化矩阵A1以及频繁1￣项集及其支持度信息，L1={{1}： 08， {2}： 0.8， {3}： 0.6， {4}： 0.8， {5}： 1};

将矩阵中原始项集及其支持度信息存贮在字典original_dic中，则original_dic={{1， 2， 3， 4， 5}： 0.2， {1， 3， 5}： 0.4， {1， 2， 4， 5}： 0.6， {2， 3， 4， 5}： 0.4}，得到确定的初始频繁项集及其支持度信息：sure={{1， 3， 5}： 0.4，{1， 2， 4， 5}： 06， {2， 3， 4， 5}： 0.4};

求解original_dic中项集间满足条件的交集commen={{1， 5}， {3， 5}， {2， 4， 5}};计算其中各项集满足条件子集的支持度信息：{{4， 5}： 08，{1， 5}：0.8，{2， 4， 5}： 0.8， {2， 5}： 0.8， {2， 4}： 0.8， {3， 5}： 0.6};

根据频繁项集的子集必为频繁项集，求初始频繁项集sure={{1， 3， 5}： 0.4，{1， 2， 4， 5}： 0.6， {2， 3， 4， 5}： 0.4}中所有项集的子集，删除已存在于not_sure以及original_dic中的子集后，其余子集支持度跟随原项集本身，则可得到sure中各项集及其满足条件子集的支持度信息：

sure={{1， 3}：0.4， {1， 3， 5}： 0.4，{1， 2}：06， {1， 4}：0.6， {1， 4， 5}：0.6， {1， 2， 4}：0.6， {1， 2， 5}：0.6， {1， 2， 4， 5}： 0.6， {2， 3， 5}：04， {2， 3}：0.4， {2， 3， 4}：0.4， {3， 4， 5}：0.4， {2， 3， 4， 5}：0.4， {3， 4}： 0.4}。

合并每一步求得的频繁项集，整理得到各个长度频繁项集及其支持度信息：

L1={{I1}：0.8;{I2}：0.8;{I3}：0.6;{I4}：0.8;{I5}：1};

L2={{I1，I2}：0.6;{I1，I3}：0.4;{I1，I4}：0.6;{I1，I5}：0.8;{I2，I3}：0.4;{I2，I4}：0.8;{I2，I5}：0.8;{I3，I4}：0.4;{I3，I5}：0.6;{I4，I5}：0.8};

L3={{I2，I4，I5}：0.8;{I1，I3，I5}：0.4;

{I1，I4，I5}：0.6;{I1，I2，I4}：0.6;

{I1，I2，I5}：0.6;{I2，I3，I5}：0.4;

{I2，I3，I4}：0.4;{I3，I4，I5}：0.4};

L4={{I1，I2，I4，I5}：0.6;{I2，I3，I4，I5}：0.4}。

得到频繁项集及其支持度信息后，根据式（2）计算相应的关联规则的置信度，例如：

Confidence（家庭年纯收入低住房为危房）=

Confidence（I1I4）

=Support（{I1，I4}）Support（{I1}）=0.60.8=075。

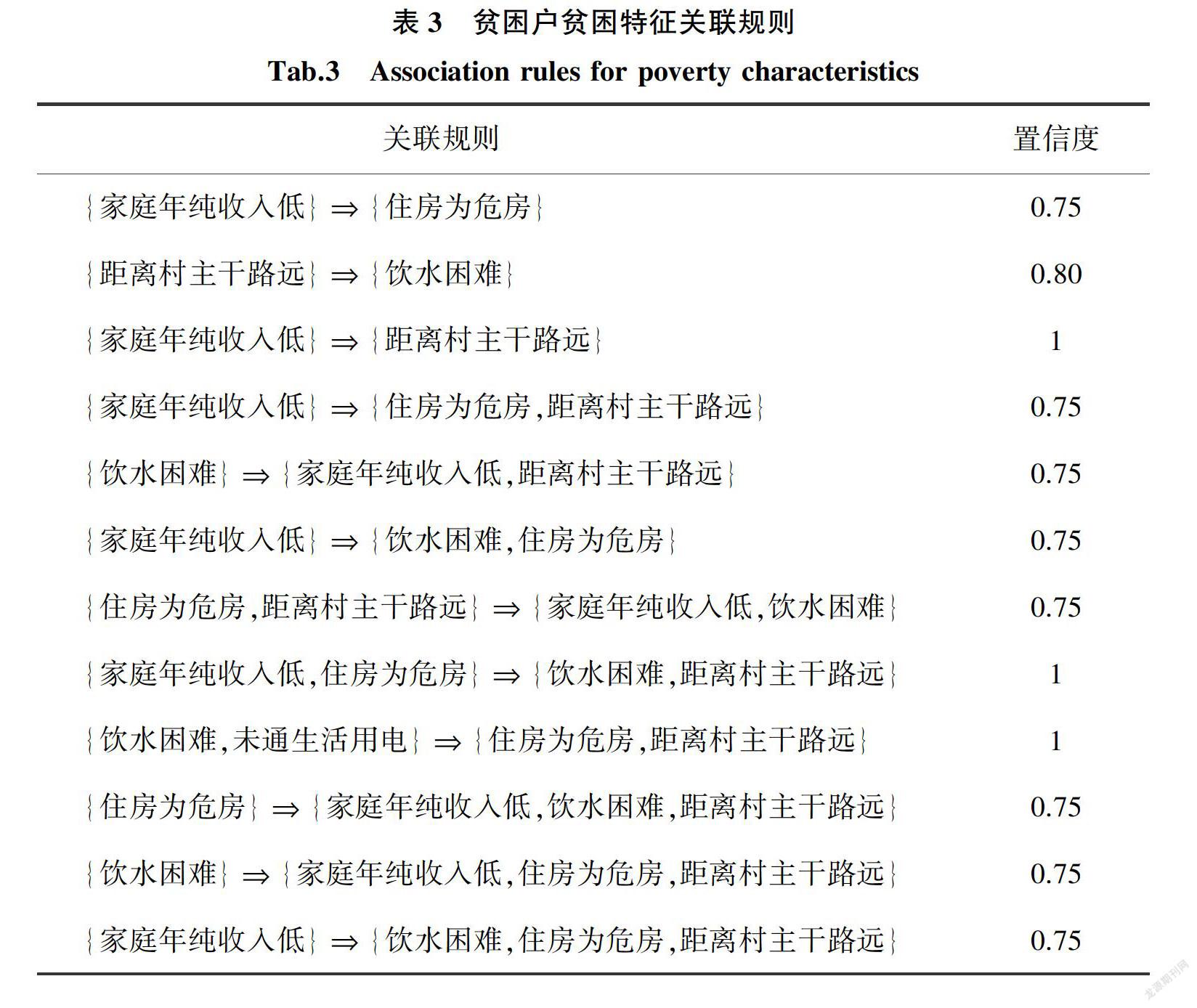
设置最小置信度值为0.7，选取结果中部分规则如表3所示。

根据上述算法实例应用，可知对扶贫数据进行挖掘，可发现各不同贫困户之间潜在的关联信息，能够更全面地考虑不同貧困户的需求，探索扶贫工作的内在规律;并且，利用所挖掘的关联信息有利于实现扶贫方式、内容与扶贫对象的有效匹配，合理分配扶贫资源，提高扶贫工作的效率与精度。

3 实验结果与分析

为比较本文所提出的Apriori_BOMS算法与传统Apriori算法的性能，在相同实验环境下，利用两

种算法对相同贫困数据集中的频繁项集进行挖掘。

3.1 实验环境与数据

操作系统：64位Windows7操作系统;处理器：Intel（R） Core（TM） i5￣6500 CPU， 3.20 GHz， 8 Gb内存;两种算法均采用Python语言编程。

实验数据为贵阳市某区7319条贫困户建档立卡数据;该数据包含贫困户家庭情况调查的多个属性，为使得数据满足算法输入要求，需对原始数据进行预处理，首先挑选了该数据集中不含有缺失值

以及较有代表性的属性（如家庭年收入、家庭人均收入、耕地面积、是否饮水困难、住宅面积等）共20个属性，并对每个属性值进行离散化，若某一条贫困户数据中“是否饮水困难”的属性值为“是”时，表示该贫困户存在饮水困难的贫困特征，因此将属性值“是”替换为相应的特征标号i，反之则置为0;当年收入或耕地面积的值低于特定数值时，将该值替换为相应特征标号i，表示该贫困户具备此贫困特征，反之则置为0，表示不具有此贫困特征，完成对属性值的处理后，得到满足算法要求的输入数据。

最后，为验证算法通用性，利用UCI数据集中的Mushroom数据对算法进行测试，该数据集包含8 124条记录，共22个属性，每个属性下有2～12个枚举值，剔除其中包含有缺省值和仅有两个有效枚举值的属性（bruises，gill￣attachment，gill￣size，stalk￣shape，stalk￣root，veil￣type），剩余16个属性，将每个属性下出现次数低于总记录数20%的枚举值置0，其他枚举值则置为当前属性的标号，得到用于测试的输入数据。

3.2 实验结果分析

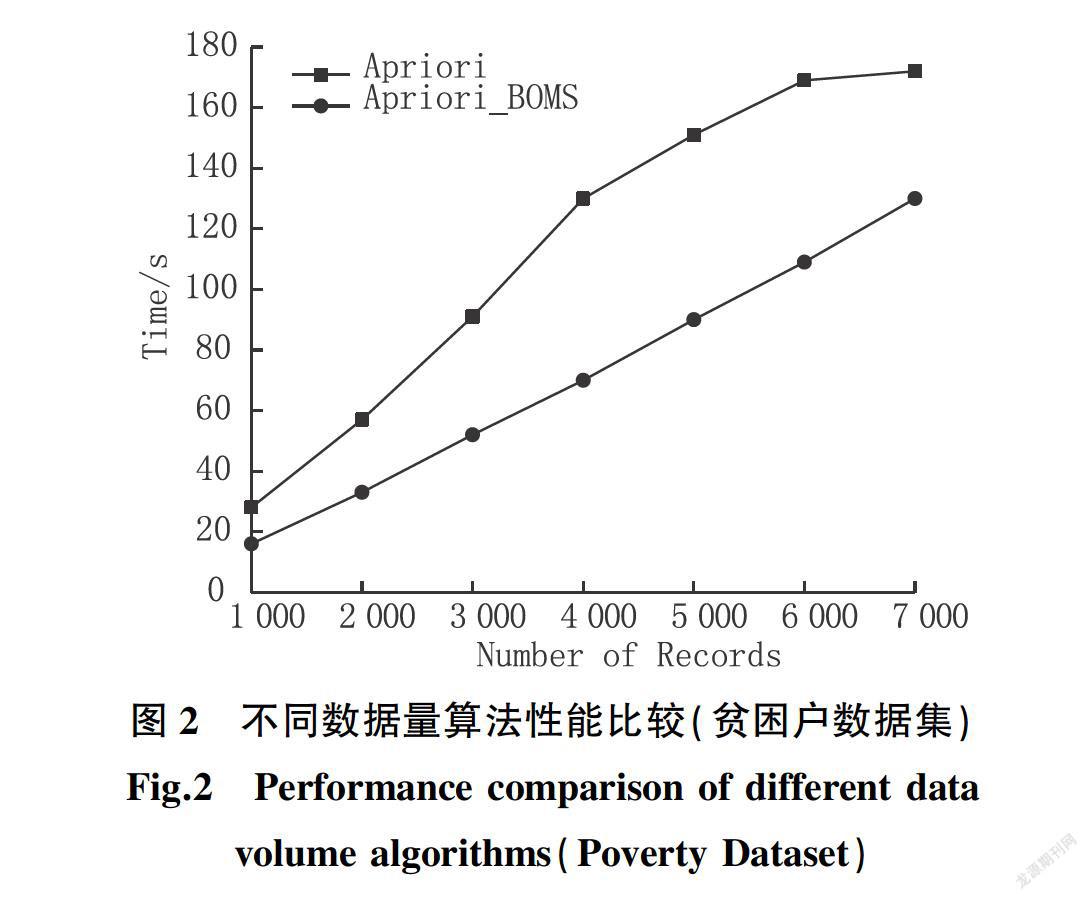
将Apriori_BOMS算法与传统Apriori算法在不同大小的数据集上进行测试，设置min_support=30%，实验结果如图2所示。由实验结果可看出本文所提出的Apriori_BOMS算法在同等数据量的条件下，运行时间明显低于传统Apriori算法。

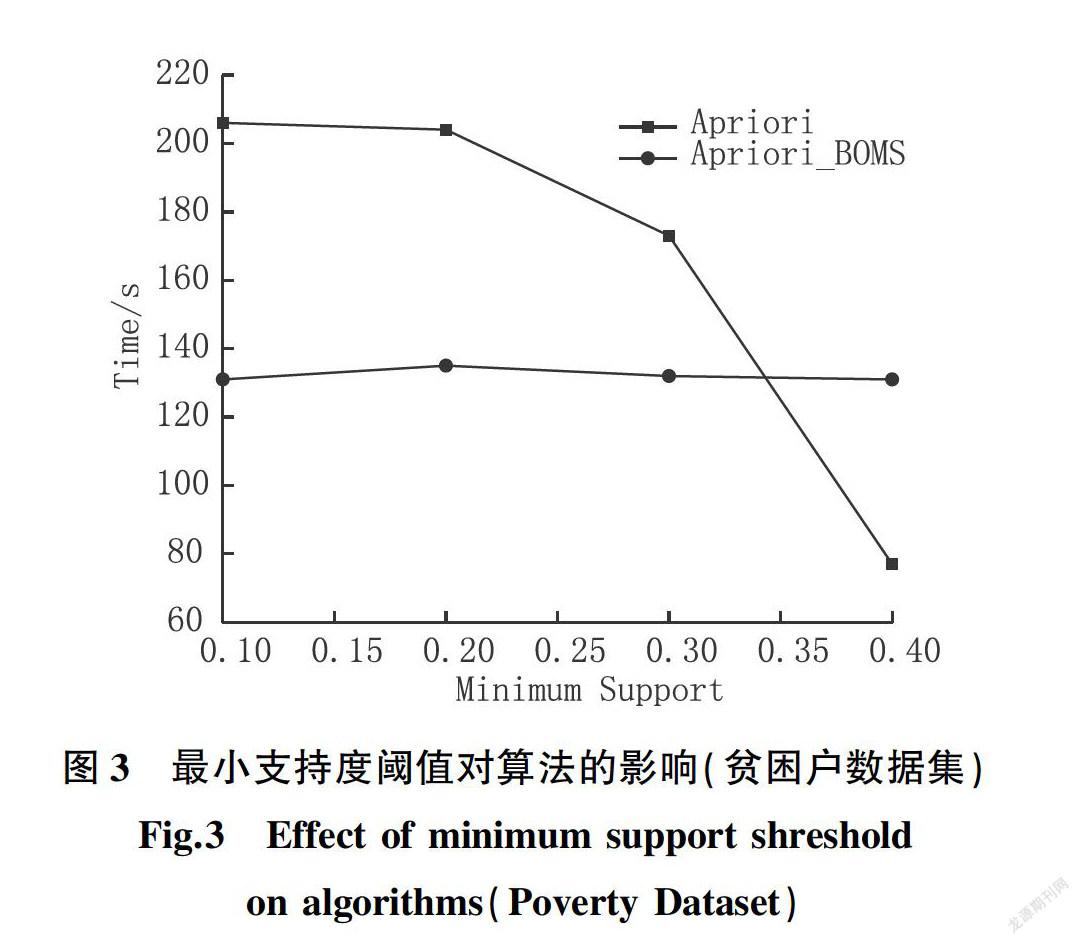
由于最小支持度阈值的改变同样会对算法性能造成影响，实际往往会设置较低的最小支持度阈值，挖掘更多满足条件的频繁项集，以此产生适应不同约束条件的关联规则。因此，改变最小支持度阈值，对比两种算法性能，实验结果如图3所示。

在最小支持度阈值低于0.34时，Apriori_BOMS算法挖掘效率明显高于传统Apriori算法，最小支持度阈值越小，两种算法的性能差异越明显;当最小支持度阈值变大使得剪枝效率增加时，传统Apriori算法性能才会改善，而Apriori_BOMS算法受最小支持

度阈值影响较小，性能更加稳定;因此，试验结果验证了本文所提出的算法能够有效解决传统Apriori算法在剪枝不理想条件下挖掘效率低的问题。

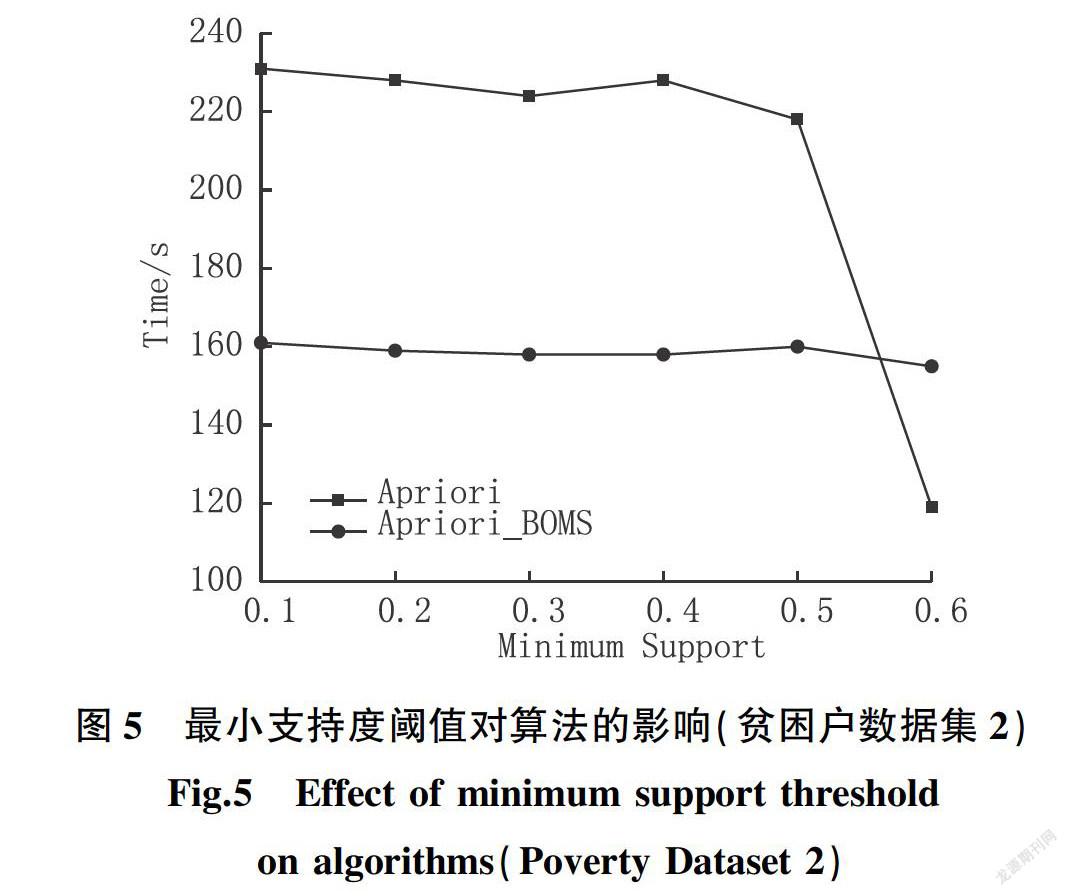
为验证本文所提出的Apriori_BOMS算法相较于传统Apriori算法在面对数据重复率高的数据集时仍具备高效的挖掘能力，对贫困户建档立卡数据属性进行离散化处理时，通过降低设置属性标号的数值，可得到属性值重复率更高的数据集（贫困户数据集2），相同实验环境下，在该数据集上测试两种算法的挖掘性能，实验结果如图4、图5所示，Apriori_BOMS性能在密集数据集下同样明显优于传统Apriori算法。

为证明Apriori_BOMS算法在其他数据集上仍具有不错效果，设置最小支持度阈值为20%，在Mushroom数据集上的测试结果如图6、7所示，由实验结果可知，Apriori_BOMS算法性能同样优于传统Apriori算法。

综上所述，本文提出的Apriori_BOMS算法解决了传统Apriori在最小支持度阈值较低以及数据重复率高条件下剪枝效果不理想而造成的挖掘效率低的问题，并且避免了多次扫描数据库，节约了系统的I/O开销;在面对数据重复率高的贫困户建档立卡数据集时，在较低的最小支持度阈值条件下仍能更加高效地挖掘数据集中隐含的有用信息，为精准扶贫工作提供助力。

4 结语

本文利用数据挖掘中的关联规则挖掘算法来发现贫困户建档立卡数据中不同贫困特征之间潜在的联系，为精准扶贫工作提供更直观的数据参考。由于贫困户建档立卡数据具有数据重复率高、属性多样的特点，传统Apriori算法在面对此类数据库时挖掘效率较低。因此，本文引入矩阵及集合间运算的概念，提出一种改进Apriori算法，通过在实际贫困户建档立卡数据及Mushroom数据集上进行测试，验证了Apriori_BOMS算法的有效性，同时，证明了该算法性能优于传统Apriori算法，在实际应用中，能够更高效地挖掘由贫困特征构成的频繁项集，支撑贫困特征关联规则的生成，助力精准扶贫工作的实施。如何对算法做进一步优化使其具备更高挖掘效率并且适用于不同数据集的挖掘将是下一步主要研究目标。

参考文献：

[1]丁翔， 丁荣余， 金帅. 大数据驱动精准扶贫：内在机理与实现路径[J]. 现代经济探讨， 2017（12）： 119-125.

[2]AGRAWAL R， IMIELINSKI T， SWAMI A N. Mining association rules between sets of items in large databases[C]// Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data. New York： ACM Press， 1993： 207-216.

[3]文武， 郭有庆. 结合遗传算法的Apriori算法改进[J].计算机工程与设计， 2019（7）： 1922-1926.

[4]李龍， 刘澎， 张可佳， 等. 改进的Apriori算法的研究与应用[J]. 计算机与数字工程， 2019， 47（6）： 1293-1297.

[5]周凯， 顾洪博， 李爱国. 基于关联规则挖掘Apriori算法的改进算法[J]. 陕西理工大学学报（自然科学版）， 2018， 34（5）： 40-44.

[6]JI Q ， ZHANG S . Research on sensor network optimization based on improved Apriori algorithm[J]. EURASIP Journal on Wireless Communications and Networking， 2018， 2018（1）： 258.

[7]于守健， 周羿阳. 基于前缀项集的Apriori算法改进[J]. 计算机应用与软件， 2017， 34（2）： 290-294.

[8]韩天鹏， 白玲玲， 王浩. 基于候选项集剪枝的Apriori算法的研究[J]. 阜阳师范学院学报（自然科学版）， 2014， 31（4）： 79-83.

[9]朱付保， 白庆春， 汤萌萌， 等. 基于改进Apriori算法的铁路轨道质量分析与评价[J]. 微电子学与计算机， 2015， 32（10）： 159-162.

[10]边根庆， 王月. 一种基于矩阵和权重改进的Apriori算法[J]. 微电子学与计算机， 2017， 34（1）： 136-140.

[11刘芳， 吴广潮. 一种基于压缩矩阵的改进Apriori算法[J]. 山东大学学报（工学版）， 2018， 48（6）： 82-88.

[12]王蒙， 方睿， 邹书蓉. 基于矩阵相乘的Apriori改进算法[J]. 计算机与数字工程， 2018， 46（10）： 1974-1979.

[13]张玺.数据挖掘中关联规则算法的研究与改进[D]. 北京： 北京邮电大学， 2015.

[14]彭敏， 黄佳佳， 朱佳晖， 等. 基于频繁项集的海量短文本聚类与主题抽取[J]. 计算机研究与发展， 2015， 52（9）： 1941-1953.

[15]刘毓， 李莎. 一种基于权重的Apriori改进算法[J].西安邮电大学学报， 2017， 22（4）： 95-100.

（责任编辑：周晓南）

An Application Research of an Improved Apriori

Algorithm in Targeted Poverty Alleviation

HE Qing*， LIU Liang

（Institute of Big Data and Information Engineering， Guizhou University， Guiyang 550025，China）

Abstract：

With the implementation of the targeted poverty alleviation archiving work， the targeted poverty alleviation system has accumulated a larger amount of data. It is of great significance to use efficient association rules algorithm to mine the hidden useful information.  The text aims at the characteristics of high repetition rate and diverse attributes of archived card data of poor households. An improved Apriori algorithm is proposed to construct candidate item sets by utilizing the data structure of the matrix and the relevant properties of the set， so as to avoid repeated scanning of the database and pruning connection operation layer by layer， so as to improve the efficiency of algorithm mining. By mining the data of the actual family in poverty， it is proved that the mining efficiency of this algorithm is better than traditional Apriori algorithm under the condition of low minimum support threshold.

Key words：

association rules; candidate item sets ; targeted poverty alleviation; Apriori algorithm