难点教学的分析与思考
戚杭燕
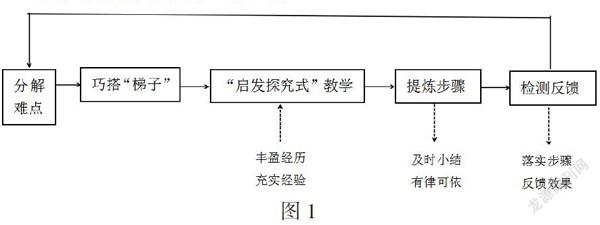
摘 要:一堂教学课中的难点是否解决,是学生对知识掌握程度高低的一个重要衡量标准,也是考试高分的密钥。本文以以探索规律型问题为例,证明巧设“梯子”,分解难点,即通过设置“归纳”、“变式”等铺垫,运用启发探究式教学,把课堂还给学生,让学生丰盈经历,充实经验,总结策略,落实步骤是难点教学有效的解决办法。
关键词:分解;难点; 规律型;探索
1.难点分解教学的基本理解
2.难点分解教学的实践分析
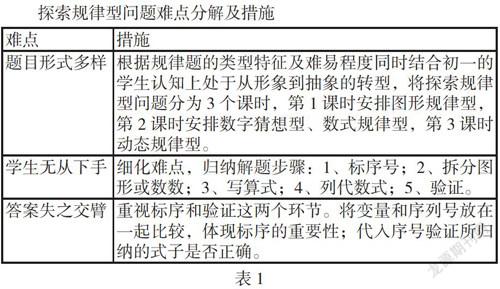
2011版《数学课程标准》对其的考试要求是“能分析具体问题中的简单数量关系,并用代数式表示”,在初中阶段,学生开始接触规律题是在学习《代数式》——“用字母表示数”之后,下表是难点及其措施:
2.1 归纳探究——活动引领,自然生长
案例:“探索图形规律”探究过程片段
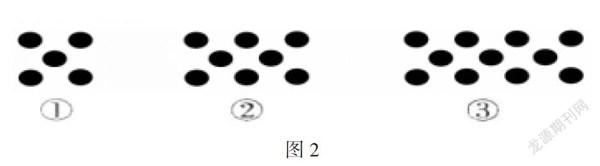
用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第5个图案需要棋子________枚,第n个图案需要棋子________枚.
学生六人小组,每个小组具备黑白棋子一盒、打印好棋子图案的纸张若干及彩色笔一盒。
方法:数出每一个图形分别对应的棋子总枚数,与序号对应,得出第n个图形中棋子的总枚数与序号的关系。
师:如何判断最后含n的表达式的规律正确与否?
生:代入n=1、2、3...到代数式,所得到的答案与前面几个图形的答案是否一致就好。
师:合作交流,概括出解决图形规律问题的一般策略。
在体验过四种图形分割的方法得到结论的具体过程后,学生能够相互补充,大胆小结,最后确定为5个步骤:
①标序号:记每组图形的序数为“1, 2, 3, . . . ,n”;
②拆分图形:数出每组图形的个数;
③写算式:根据拆分方法列好每一幅图形对应的分解算式;
④列代数式:寻找第n项(某项)的个数与序数n的关系:观察算式是由不变的数字和变化的數字组成。由不变的数字得出结构,再用变化的数字与序号进行对应,写出与序号n的关系然后按照定量变化推导出关系式;
⑤验证:代入序号验证所归纳的式子是否正确。
3.对难点分解教学的思考
数学教学,不是灌输,也不是告诉,而是一个不断探索、慢慢发现的过、逐步积累的过程。它借助“探索图形规律”为问题,以图形规律变换为“根”,以拆分图形为“线”,以算式转换为代数式为“路”,思维慢慢深化,逐步积累经验。让学生在“做”中经历过程,在解决问题中攻克“磨难”,品尝探索的艰辛及成功的喜悦。
参考文献:
[1] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012:27
[2] 严群亚.在初中数学教学中巧用铺垫化解难点策略探讨[J].中小学教学研究,2015(5):17.

