大跨径桥梁施工中空气静力的特性研究
钟炜林

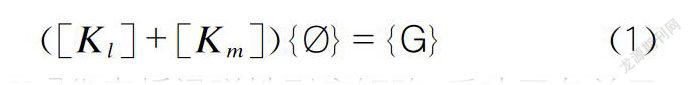


摘要:文章基于大跨径桥梁施工技术的发展现状,分析了当前空气静力特性理论的研究与应用情况,阐述了空气静力稳定性的有限元模型分析方法、结构几何计算方法以及静力载荷计算方法,总结了研究中需注意的问题,并通过工程实际案例,完成了空气静力特性试验,研究了桥体主梁空气静力载荷与振动临界风速之间的关系。
关键词:大跨径;桥梁施工;空气静力;研究
中图分类号:U441 文献标识码:A DOI:10.13282/j.cnki.wccst.2019.09.041
文章编号:1673-4874(2019)09-0146-04
0引言
随着我国桥梁工程技术的不断发展和进步,越来越多高难度、高技术含量的桥梁在不断施工建设,为提高各地区交通运力、带动当地经济发展起到了至关重要的作用。大跨径桥梁的施工因工程质量高、施工难度大被视为桥梁工程届的难题.近年来,通过我国工程技术人员的长期探索和工程试验,在大跨径桥梁施工方面积累了很多宝贵的经验,经过该领域的专家和学者们的共同努力,现阶段大跨径桥梁的施工技术已取得了一定的成果并逐渐走向成熟。港珠澳大桥的顺利通车使得我国在国际上大跨径桥梁施工领域中的地位进一步突显。于2019-05-01前通车的虎门二桥无论在施工技术、施工设备以及施工验收标准方面都处于国际领先地位,为粤港澳大湾区经济带的建设提供了有利支撑。本文以大跨径桥梁施工技术的发展现状为研究背景,从大跨径桥梁施工技术的难点出发,分析了空气静力特性理论,通过有限元模型的方法研究了空气静力对桥梁的影响。本文研究内容可为大跨径桥梁施工中的空气静力特性研究提供参考,具有相应的工程应用价值。
1大跨径桥梁施工技术发展现状
我国桥梁工程在经过30多年的发展之后,桥梁结构在逐渐变轻,桥梁的载荷与跨度在逐渐增加,这与桥梁工程领域新施工材料和施工技术的发展密不可分。新时期为适应各领域建设的需要,如山峰景区、跨海通行等,在大跨径桥梁的施工与建设方面,对建筑材料、施工工艺、桥梁美学以及桥梁整体质量也提出了更高的要求。当桥梁跨度超过500m时,桥梁的应力几乎已达到极限值,只有提高施工材料的标号才能适应桥梁跨度增加的需要。在斜拉桥的施工中,可通过使用碳纤维材料代替钢索的方式来增加桥梁跨度。因此,为不断满足日益增加的桥梁跨度需求,使用新型的施工材料和施工工艺是必然趋势。未来大跨径桥梁的施工材料将向着强度高、重量轻的方向发展,在载荷能力、抗风险等级方面也均有显著的提高。
2 空气静力特性理论研究与应用情况
新施工技术和施工材料的不断应用使得桥梁的跨径在不断增加,当桥梁的跨径达到一定值时将给工程主体的施工带来相应难度,同时也会带来一系列的工程问题,如空气静力特性中结构失稳的情况。空气静力失稳情况通常在桥梁遇到强静风作用时发生,使得桥梁弯曲或扭转,使桥梁的结构刚度发生改变,同时也改变了桥梁的静风载荷能力,进一步增加了桥梁结构的形变,并最终引起桥梁结构失稳,桥梁扭转、移位会进一步造成风攻角的改变,进而反作用于桥体结构的静风载荷。我国在空气静力特性理论方面的研究比较深入,在《大跨径桥梁施工抗风设计规范》中,对强风情况下的桥梁结构状态进行了说明,具體来说将桥梁的失稳状态分为侧倾和扭转两种,在小变位状态基础上通过二维模型推导出失稳状态的临界计算公式,也可通过三维建模方法来求得大跨径桥梁的空气静力扭转极限风速。不同中跨跨径下的空气静力失稳临界风速对比如表、所示。
3 空气静力稳定性的有限元分析方法
随着计算机和网络技术的迅速发展,在桥梁工程施工中有限元分析方法也得到了广泛的应用,并成为研究桥梁结构稳定性的主要方法。常见的有限元分析系统有ANSYS和MIDAS等。本文研究过程采用ANSYS有限元分析方法,讨论大跨径桥梁的空气静力稳定性。
3.1桥梁结构有限元模型
有限元模型分析的基本要求是在保证桥梁结构合理的同时简化计算模型,并维持桥梁结构良好的质量、刚度。以桥梁的主梁施工为例,通常有单梁、双梁以及三梁等几种建筑模型。单梁模型较常见,在此模型中,轴线经过主梁的断面扭心,使得整个梁体刚度、质量分布以及质量惯矩在轴线上集中。该模型在扭转刚度较大的箱梁中较为适用。依据空间杆系的稳定性理论,桥梁空气静力特性问题可归类为如下非线性方程模型:
([K]+[K]){φ}={G} (1)
其中汇[K]代表桥梁弹性刚度矩阵,反映了各单元截面刚度情况;[K]代表桥梁几何刚度矩阵,与桥梁结构中各单元几何长度、位置以及各单元自身轴力相关。[K]与[K]将随着桥梁结构的变化而变化。{G}代表桥体结构所受阻力的函数;{φ}代表阻尼系数.通过迭代法求解此非线性方程。在求解过程中考虑到桥梁结构的空气静力响应程度,将阻力、升力以及扭矩按照分段直线的方式拟合。在求解发散风速时,确定攻角后假设初始风速为V,由桥梁空气静力响应曲线得到相应的主梁扭转角度,以此作为新一级风速状态进行再次计算,直到计算结果收敛为止。而此时求出的风速便是桥梁空气静力状态下的临界失稳风速。不同临界风速求解方法的比较分析如表2所示。
3.2结构几何计算方法
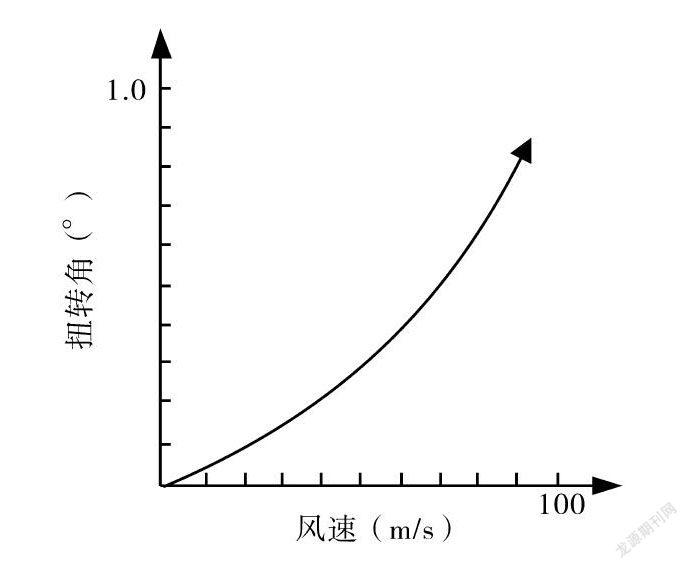
结构几何计算方法是指桥梁结构的形变达到阈值后,桥梁所受应力和桥体位移之间不再具有线性关系。而且桥梁总体刚度取决于各单元刚度,即某个单元发生位移后,该单元会影响桥梁总体的刚度变化。单元位移变化包括单元的形状和位置的改变,在某种情况下,刚度和位移彼此影响、相互作用。桥梁结构中面外的刚度受结构面内应力影响较大,面内应力与刚度间共同构成应力刚化。值得注意的是,悬索及吊杆发生应力刚化的程度在桥梁的主跨结构中较为显著,主跨扭转位移趋势曲线如图1所示。
3.3 静力载荷计算方法
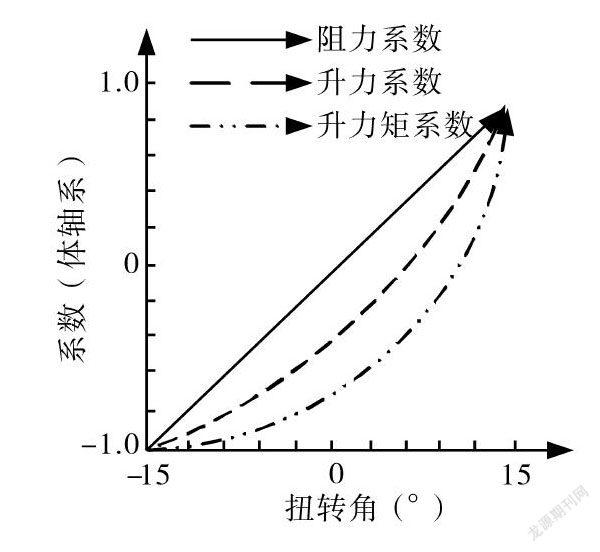
静力载荷是指在静风载荷作用下,桥梁载荷的大小随桥梁结构的变化而变化的情况。一般而言,大跨径桥梁施工过程主要包括主梁、悬索以及吊杆等部分,且主梁、悬索以及吊杆部分的施工仅考虑静力载荷中的阻力因素。假设桥梁在形变过程中上述工序在静力载荷情况下所受阻力大小恒定,并且将主梁部分所受静力载荷细分为三个层面的分力,即阻力、升力以及扭矩,则在风速等级不断增加的过程中,主梁结构将发生扭转,进而使阻力、升力以及扭矩的计算系数发生改变,最终引起主梁上静力载荷变化。因此,可将主梁所受静力载荷视作其形变的函数。主梁静力系数曲线如图2所示。
3.4 其他需要注意的问题
(1)体轴坐标系的选用原则
如果选用体轴坐标系进行桥梁静力载荷计算时,要注意体轴坐标系应与有限元模型计算时所用的坐标系一致,以尽量减少桥梁静力载荷在各坐标系之间的转换过程,最大程度上节约计算资源,从而降低求解所耗时间。
(2)体轴坐标系的适用范围
在体轴坐标系情况下,静风载荷的计算过程仅与主梁实际发生的扭转情况有关。具体来说通过主梁的扭转角来衡量,与风攻角无关。但在风轴坐标系情况下的静力载荷则与风攻角有关,这里所指的攻角为风的初始攻角。因此,为便于静力载荷的加载和计算,试验过程应在体轴坐标系下完成。
4工程实例分析
以广西柳州某连续箱梁悬索桥工程为例,计算该桥主梁空气静力载荷数值。在0°攻角情况下,通过有限元非线性振动分析程序,选取该桥主梁部分节段进行静力分力(阻力、升力和升力矩)系数测试。其中,桥梁结构的阻尼比为0.5%,分析上述分力对于大跨径悬索桥的空气静力稳定性影响。
4.1工程概况
该桥主跨410m,主缆由五跨构成,成桥情况下跨径组合为(22.385+152.146+410.0+152.146+22.385)m。主跨的垂跨比為1:9,吊索位于中跨,桥塔侧吊索与桥塔中心水平距离为10m,其他吊索的水平距离也为10m。主缆使用平行索股(PPWS)。
4.2 主梁空气静力载荷分析
空气静力非线性效应对于临界振动风速的影响分析如表3所示。由表3线性、非线性数据比较可知,空气静力与桥体结构彼此作用的非线性结果使桥梁振动的临界风速提高了3.1m/s,增幅近5%。这表明空气静力与桥体结构彼此作用的非线性效果在大跨径悬索桥的稳定性影响因素中比较显著。振动临界风速值的增加,与空气静力情况下主梁的扭转形变产生的负攻角有关。通过工程经验值可知,在风洞试验过程中,在攻角为-3°时的稳定性高于0°,主梁的扭转形变而形成的负攻角对于提高桥体结构的稳定性具有积极作用。当仅考虑静力非线性而不考虑空气动力情况时,振动临界风速相比于线性分析提高了0.7m/s,即振动临界风速值的提高与桥体结构内力的变化相关。
5 结语
本文以当前我国大跨径桥梁的施工技术和工程问题为研究背景,对大跨径桥梁施工中的空气静力特性进行了深入研究,在桥梁结构的有限元模型、桥梁结构的几何计算以及桥梁结构的静力载荷计算方面进行了详细讨论。在工程实例分析中,通过广西柳州某连续箱梁悬索桥的空气静力特性试验,阐述了桥体主梁空气静力载荷与振动临界风速之间的关系。本文研究内容可为我国大跨径桥梁施工中的空气静力特性研究提供参考,具有一定的工程实用价值。

