码头工程建设对长江中游典型河段水流影响的数值模拟研究

文章编号：1006-0081（2019）09-0018-04

摘要：为了研究码头工程建设对荆江公安河段河道水流的影响，通过建立平面二维水流数学模型，计算分析了工程建设前后附近河段的水位、流速变化情况。结果表明：工程建设对其所在河段的水位和流速影响较小，不会对工程河段河势、行洪带来较大影响。建立的二维水流数学模型可准确模拟工程河段水流运动特性，可为研究工程前后河道水流、水位变化提供较为可靠的依据。

关键词：水位;流速;数学模型;码头工程;公安河段;长江中游

中图法分类号：TV147

文献标志码：A

DOI：IO.15974/j.cnki.slsdkb.2019.09.004

1概况

1.1河段概况

长江是我国第一大河流，其干支流通航里程已超过6.5万km，占全国内河的52%，水运量占80%，是沟通我国东、中、西部地区的水路运输大动脉，在流域经济社会发展中具有极其重要的地位，素有“黄金水道”之称。目前，长江干线已成为世界上运输最繁忙、运量最大的通航河流。与其他交通运输方式相比，长江水运具有占地少、成本低、能耗小、污染轻、运能大、效益高等优势。随着水运经济的发展，长江沿岸码头工程的数量越来越多，码头对附近水域产生的阻水作用很有可能对该河段的河势及行洪产生影响。因此，研究码头建设对其所在河段水流的影响极为必要。本文以荆江公安河段左岸某码头工程为例，采用平面二维水流数学模型，对工程建设前后的河道水流流速、水位的变化情况进行了模拟计算，为该河段工程建设提供技术支撑。

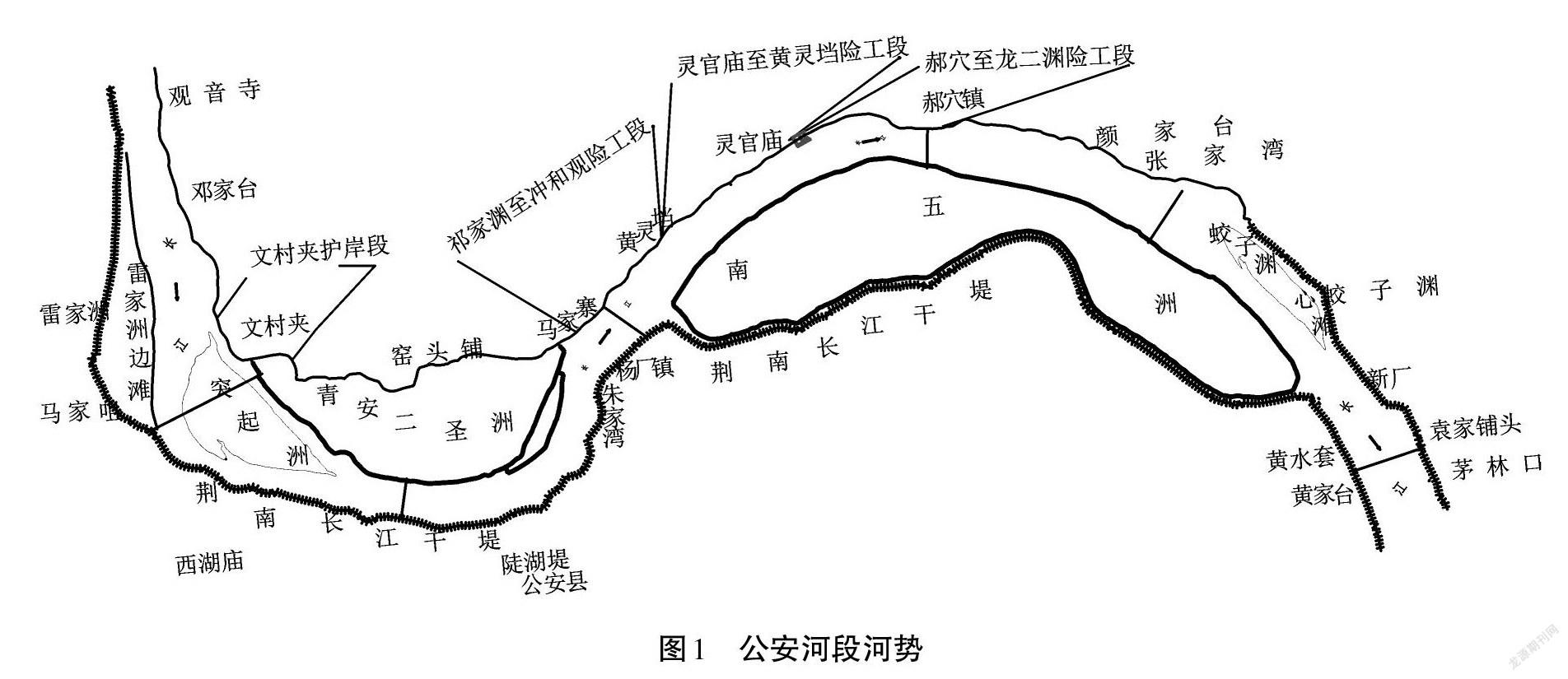
长江公安河段上起观音寺，下止新厂，全长约54km，由陡湖堤河弯、郝穴河弯及过渡段组成，河型为微弯分汊。据历史资料记载，白元朝至1756年，陡湖堤至郝穴河段为单一的微弯河段，从观音寺到马家寨，河道紧靠现在的荆江大堤。1830年后，随着陡湖堤河弯南岸不断崩塌，河面不断展宽，逐渐形成突起洲。郝穴河弯中的采石、白沙、新淤、新泥和白脚等5个江心洲将河道分为左、右两汊，左汊为主河槽，右汊即黄水套。1852年起，郝穴一带开始實施护岸，由于历年泥沙的不断淤长，采石洲等5个江心洲逐渐联成一个整体，成为现在的南五洲。近30a来，公安河段河势演变基本平稳，岸线、深泓及滩槽位置相对稳定。随着三峡水库蓄水运用，大量泥沙被拦截在库内，下泄泥沙量大幅度减少，公安河段冲刷强度普遍增[1-2]，公安河段河势见图1。

1.2工程概况

码头工程位于荆州市江陵县郝穴镇城区上游，长江左岸的郝穴作业区，对应荆江大堤桩号为鄂江左712+492-712+960。上距在建的荆州长江公铁大桥约4.5km、距沙市水文站约45km，下距江陵县城约3km。

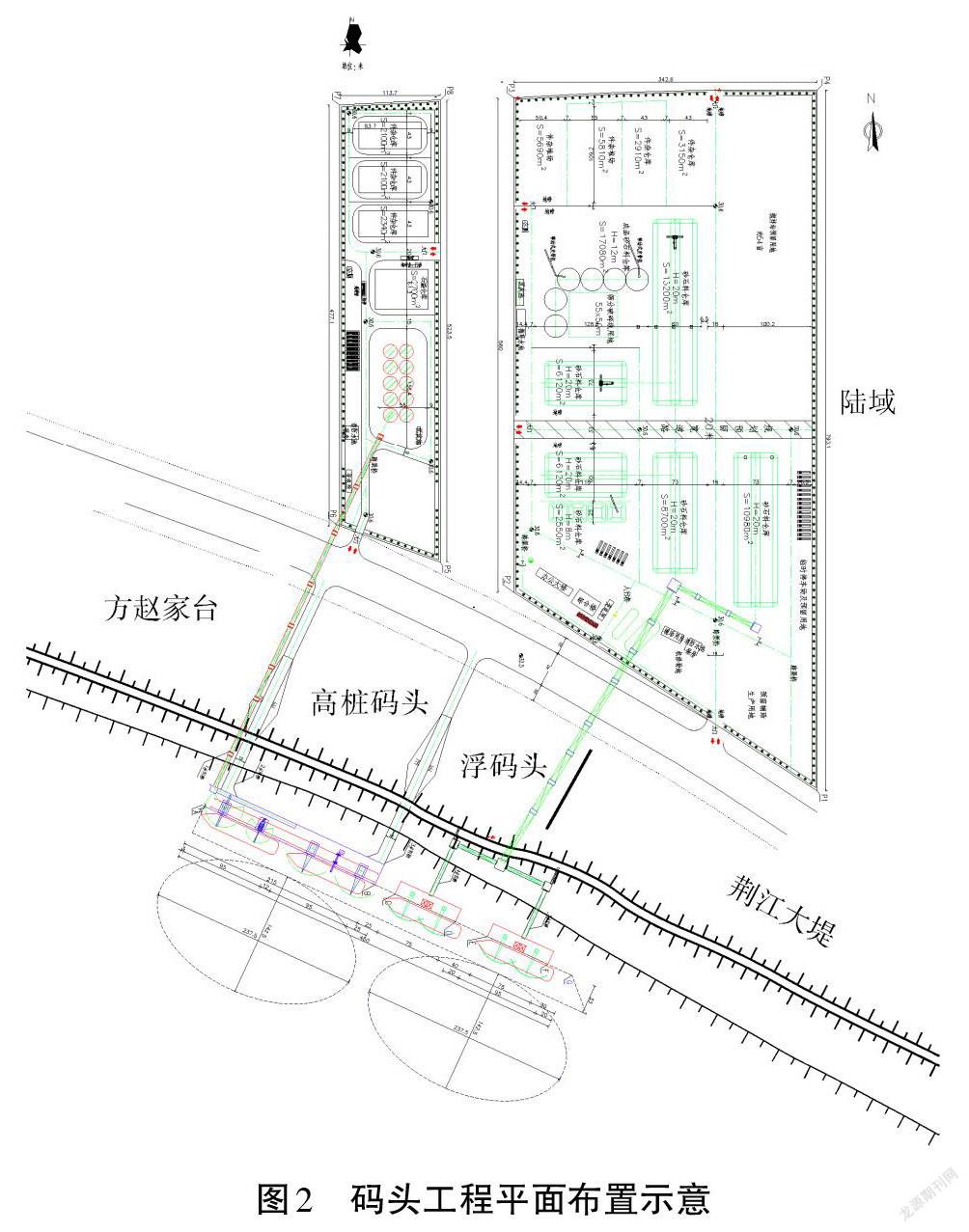
码头工程水工建筑物主要为4个3000吨级货运泊位，包括高桩直立式码头1座，浮码头2座（见图2）。为了减少码头对荆江大堤的不利影响，码头采用顺岸布置，码头前沿线与上游中航粮油综合码头前沿线呈折线，夹角为174°，布置丁21-22m等高线附近，与水流方向基本一致。泊位总长468m。

高桩码头平台长220m，宽25m，顶标高40.5m。码头平台通过2座引桥和1条皮带机廊道分别与大堤和后方陆域廊道相接，上游1号固定引桥长58.4m，宽12m，下游2号固定引桥长75m，宽12m，2座引桥与大堤平交后，通过下堤道路与规划道路连接。皮带机廊道布置在1号固定引桥的上游侧，采用多跨钢引桥结构跨堤，并与后方陆域廊道对接。

浮码头每个泊位从江侧往大堤方向均设置1艘75.0mx16.0m（长×宽）钢质趸船、2座钢撑杆系统、1座60mx4.5m（长×宽）活动钢引桥和1座转运楼墩台，墩台顶高40.77m。两个转运楼墩台之间各通过1座钢引桥连接到2号转运楼墩台，墩台顶高程47.70m，2号转运楼墩台通过固定钢引桥与后方陆域连接，引桥全长360.74m，宽8m。

2模型原理

本次数学模型基于正交曲线坐标系下沿水深平均的平面二维水流运动方程组，微分方程的数值离散采用有限体积法[3-8]。定解条件包括初始条件与边界条件，边界条件为上游给定垂线平均流速沿河宽的分布，下游出水位沿河宽的分布。对于岸边界，则采用水流无滑移条件，即取岸边水流流速为0。在计算时，由计算开始时刻上、下边界的水位确定初始条件，初始流速取0，随着计算的进行，初始条件的偏差将逐渐得到修正，对最终计算结果的精度不会产生影响[9]。

3模型建立与验证

3.1模型建立

模型选取观音寺附近至茅林口全长约49.15km的河段作为二维数学模型的计算区域（见图1）。计算河段的地形资料采用2016年10月实测地形资料。

计算网格采用正交曲线网格，在工程河段布置600x120个网格，其中ξ方向网格数600个，平均断面间距8lm;η方向网格数120个，平均网格宽度约33m。同时，为使网格大小与工程实际尺寸一致，对工程附近的局部河段进行了网格加密处理。

3.2模型验证

采用2014年12月该河段实测的水面线与垂线平均流速资料进行水位与流速验证。水位验证成果见表1，流速验证成果见图3。水位、流速计算值与实测值基本一致，水位误差大部分在5cm以内，流速误差在0.1m/s之内，符合JST/T231-4-2018《内河航道与港口水流泥沙模拟技术规程》要求。因此，模型中相关参数的取值是合理的，可以模拟码头修建对河道水位与垂线平均流速的影响。

4工程影响计算分析

4.1工程概化

码头工程主要阻水建筑物为桩柱、墩台，在防洪设计洪水时还有现浇承台及部分引桥桥面。为在模型中反映码头工程对河道水流的影响，在网格剖分时，尽可能在码头附近对网格进行局部加密，同时采用局部地形修正与局部糙率调整来进行概化处理。

（1）工程桩柱增加了过水濕周，从而引起阻力的增加。由于码头桩基尺寸小于网格尺寸，采用局部糙率修正的方法进行概化[10]，即桩柱处局部综合糙率为

np=√ n12+n22 （1）式中，np为修正后的局部糙率;n1为桩壁面糙率;n2为河道糙率。

（2）将码头平台、桩柱等的阻水面积平均加高到相应位置的计算网格节点上，以考虑建筑物的阻水作用。

4.2计算条件

码头上游约45km处有沙市水文站，其间没有大的支流人汇，沙市站流量可代表公安河段来水量。计算工况有以下3种，结果详见表2。

（1）1998年洪水的防洪设计洪水条件。1998年沙市站实测最大流量为53700m3/s，相应水位45.22m（冻结吴淞高程）。由丁沙巾市站至拟建码头间无大的支流，因此1998年拟建工程处最大流量取53700m3/s，通过水面比降推得相应水位为40.52m。

（2）防洪设计洪水条件。根据《长江流域防洪规划》，沙市同水位的流量值主要受荆江与洞庭湖汇合口城陵矶水位影响。同样地，沙市、城陵矶水位低，则泄量大;城陵矶水位高，顶托影响增加，泄量就小。根据近年资料分析，当沙市站水位为防洪设计水位45.0m（相应城陵矶水位34.40m，冻结吴淞高程）时，相应泄量采用53200m3/s，因此拟建工程处防洪设计洪水取53200m3/s，相应水位为40.13m。

（3）平滩流量条件。沙市站的平滩流量约为30000m3/S，因此拟建工程处平滩流量取30000m3/S，相应水位为36.35m。

4.3计算成果分析

4.3.1工程阻水比

码头工程阻水面积如表3所示，表中统计数据所在统计断面为过水断面面积变化幅度最大的断面。

4.3.2壅水计算分析

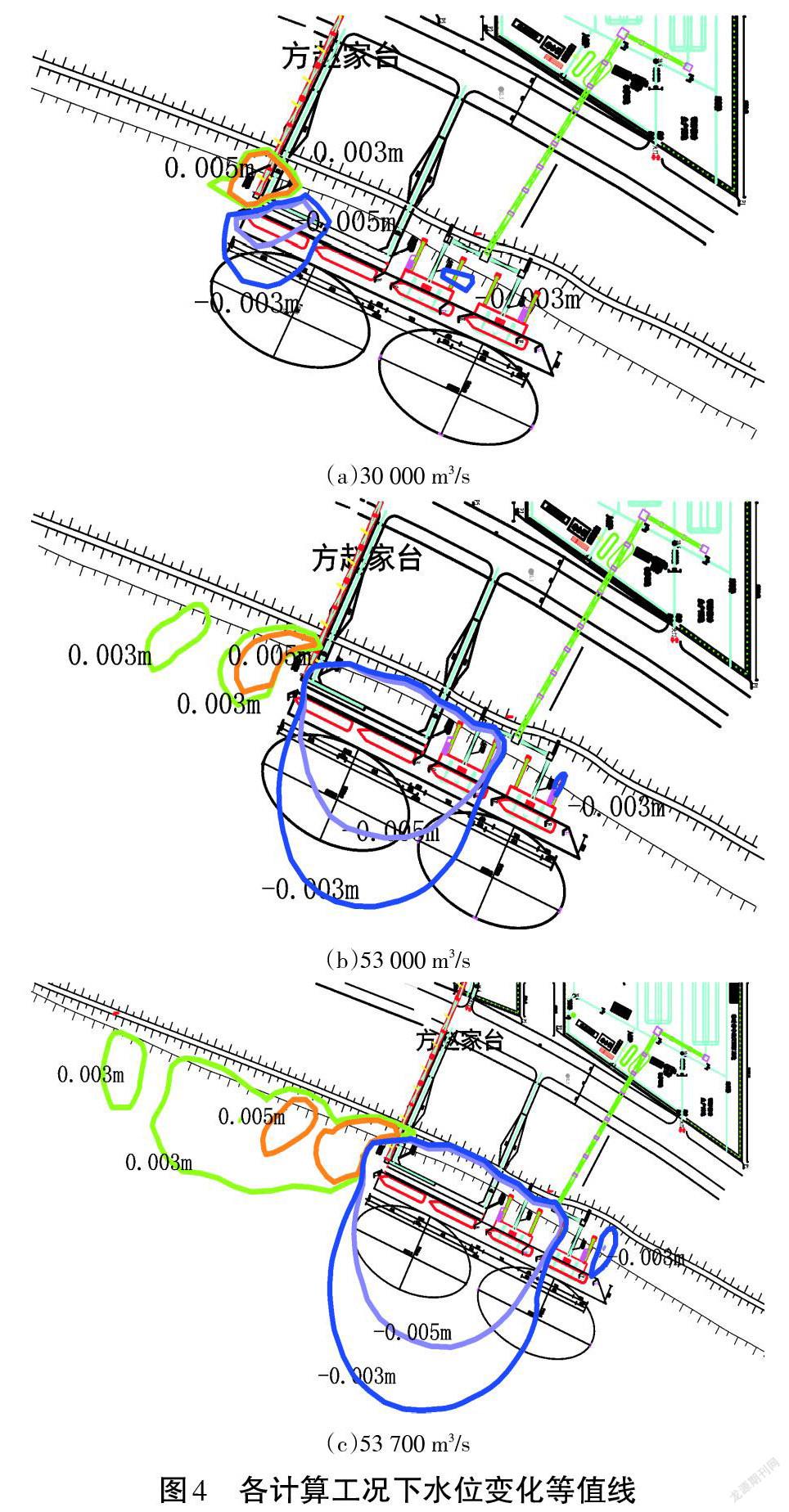
码头工程修建后，河道水位的变化主要集中在码头附近的局部区域内，具体表现为工程上游水位壅高，而其下游水位则有所降低。在不同的上游来流条件下，水位的变化趋势基本一致，但变化幅度不同。选取水位变化dz=0.003m和0.005m两条等高线绘制水位变化等值线图（见图4），水位变化结果见表4。

4.3.3流速影响计算分析

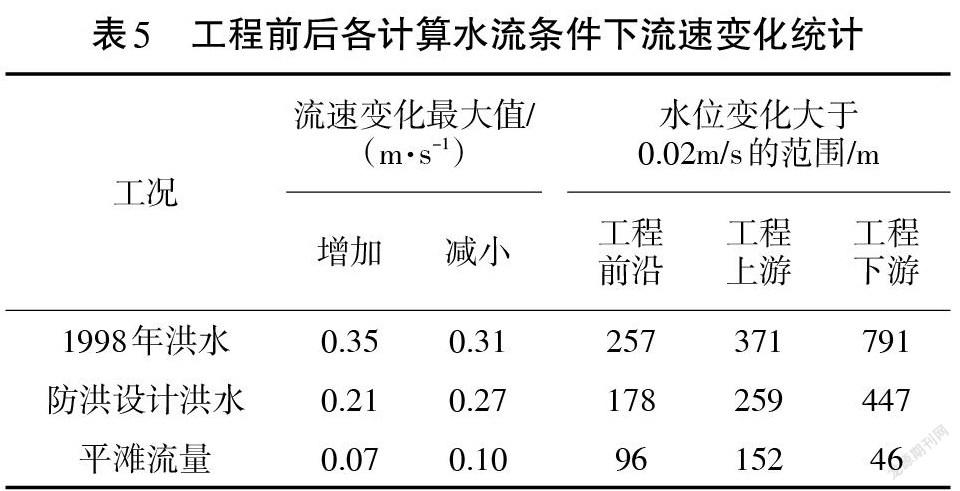
工程对流速的影响主要集中在工程上、下游及码头前沿的局部区域内，且影响范围随着流量的增加而增大。选取流速变化dv=O.Olm/s和0.02m/s两条等值线绘制流速变化等值线图（见图5），流速变化结果见表5。

5结论

本文通过建立平面二维水流数学模型，计算了码头工程建设前后附近河段的水位、流速变化情况。数学模型验证表明：流速、水位的计算值与实测值较为一致，模型能较好地反映公安河段的水流运动规律，因此将该模型用于计算分析该河道是可行的。计算结果表明：①1998年洪水条件下，码头附近水位变化的最大值为0.028m，变化值大于0.003m的范围最远到达工程上游约572m。工程修建对水位变化的影响较小。②1998年洪水条件下，码头附近流速变化的最大值为0.35m，变化值大于0.02m/s的范围最远到达工程下游约791m。工程修建对流速变化的影响较小。因此，码头工程建设对河道水流的影响较小，不会对工程河段河势、行洪带来影响。

参考文献：

[1]周成成.三峡水库蓄水后荆江河段河床冲淤及水位变化特点分析[C]//三峡工程运用10年长江中游江湖演变与治理学术研讨会，2013.

[2]许全喜.三峡水库蓄水以来水库淤积和坝下冲刷研究[J].人民长江，2012，43（7）：1-6.

[3]于日旻.正交曲线坐标系下复杂边界二维水流数值模拟研究[D].大连：大连理工大学，2006.

[4]周雪漪，计算水力学[M].北京：清华大学出版社，1995.

[5] 谢鉴衡.河流模拟[M].北京：水利电力出版社，1990.

[6]谢作涛，张小峰，袁晶，等，一般曲线坐标系平面二维水沙数学模型研究与应用[J].泥沙研究，2005（6）：58-64.

[7]张为，何俊，袁品，等，二维水流数学模型在马家咀航道整治工程防洪评价中的应用[J].中国水运（下半月）， 2010， 10（12）： 190-192.

[8]赵建锋，李国斌，尚倩倩.长江下游江心洲河段航道整治工程防洪评价[J].人民长江，2013（S1）：73-75.

[9]简秋敏，刘轶，李子龙，等.松虎航道整治工程水流数学模型的建立与应用[J].水利水电快报，2016，37（7）：27-31.

[1O]张细兵，余新明，桥渡壅水对河道水位流场影响二维数值模拟[J].人民长江，2003，34（4）：23-24.

（编辑：李晓潆）

收稿日期：2019-04-08

作者简介：吴国君，女，工程师，主要从事港口航道工程设计等方面工作。E-mail： 542640865@qq.com