破碎机锤轴转动对爆炸过程影响的数值模拟

程 科,叶文华,冯 阳,肖磊明,陈阳明,王一茹

(1.南京航空航天大学机电学院，南京 210016；2.南京航空航天大学经济与管理学院，南京 210016)

当前国际上最先进的废金属处理方法，在我国已逐步得到了推广应用，其废金属破碎处理过程为：金属废料通过加料输送装置提升至碾压装置，经挤压整形后进入破碎机；破碎机主轴转子上的锤头轮流击打废料，引起废料碎断[1-5]。由于破碎处理的废油罐、废气罐、废油漆桶、废危化品罐、废压力容器之类的废金属料中常含有易燃、易爆危险废料，在废金属料破碎与击打过程中，当破碎腔内部产生火星或温度与气体浓度达到一定条件时，就有可能发生爆炸和燃烧。近几年，我国在废金属破碎处理过程中起火、爆炸事故时有发生，造成了不小的人员伤亡与生产设备损坏。因此研究破碎机内部的爆炸规律，制定合理的防爆、抑爆、隔爆、泄爆方案，对废金属处理有着重要意义。

破碎机体积较大，搭建破碎机实体机的实验平台较为困难，因此需要采用数值模拟的方法对破碎机实体机内的爆炸过程进行分析。在具有边界运动的数值模拟方面，张凌新等[6]、汪家琼等[7]基于滑移网格技术数值模拟了离心泵的内部流场，分析了LES和RANS两种模型在模拟旋转流场时，瞬态流动特征的不同以及固体颗粒物的磨损特性；高飞飞等[8]采用滑移网格的方法计算螺旋桨滑流，研究了全机流场和气动性能受螺旋桨滑流影响的规律；肖根福等[9]对涡旋压缩机的内部流场进行三维仿真，采用动网格技术，对涡旋压缩机动态流场进行数值模拟；傅德彬等[10]基于动网格技术模拟了导弹发射过程中的非定常流场,提供了非定常计算燃气射流及分析导弹筒内运动状态的可行方法；杨康等[11]采用基于MRF模型的CFD数值分析方法，得到了不同转速下桨叶的扭矩值和拉力。在易燃、易爆气体的爆炸实验研究与数值模拟方面，A.D.Benedetto等[12]研究了不同组分条件下易燃气体爆炸压力和爆炸极限，总结出爆炸压力、爆炸极限随组分变化的规律；陈鹏等[13]、S.S.Ibrahim等[14]研究了存在障碍物条件下的爆炸过程，得到了障碍物形状、排布方式、阻塞率等对爆炸火焰加速的影响规律；洪溢都等[15]对开口型管道内瓦斯爆炸产生的冲击波动压进行数值模拟，得到了动压的传播演化规律，并给出定量描述。

从以上研究可以看出，对于具有运动边界的数值模拟研究已经有了一定的研究基础，广泛应用于离心泵、螺旋桨、压缩机等内部流场分析。但是在爆炸规律研究过程中，对运动边界可能造成的影响缺乏足够的研究，过多的考虑压力、温度、组分等对爆炸影响，对于边界简化过于理想。本文介绍了在前人研究的基础上，以常见的易燃、易爆气体甲烷作为模型气体，利用Fluent数值模拟软件建立滑移网格模型，对存在锤轴转动的破碎机内部进行数值模拟，研究其在锤轴转动下的爆炸规律。

1 数值模型建立及验证

1.1 数值模型建立

以锤式废金属破碎机为研究对象，箱体结构如图1所示。其基本尺寸为4 400 mm×2 760 mm×4 150 mm，锤轴直径为1 800 mm。正常工作时锤轴转速60 rad/s左右。

图1 破碎机箱体结构Fig.1 Structure of crusher body

选用Fluent作为计算软件，采用压力基瞬态求解器，基于RNGk-ε湍流模型和EDC燃烧模型进行求解运算。边界设置：数值模拟对象为密闭破碎机内的爆炸，无进出口条件，壁面为绝热无滑移，温度梯度为0，湍动能k=0，湍流耗散率ε=0；将破碎机内腔转动区域设置为绝对转动滑移区域(见图2)，转动区域的壁面条件设置为Movewall，构建转动区域与静区域的交界面为一对Interface面，Interface面的作用是实现转动区域与静区域之间的压力、温度、动能等数据的传递。

图2 破碎机内腔模型Fig.2 Internal cavity model of crusher

转动区域与静区域内初始条件如下：

1)甲烷-空气充分混合，均匀分布在计算区域内，甲烷的体积分数为9.5%，氧气和氮气满足空气中体积比；

2)初始温度300 K；初始压力为0 Pa;

3)点火条件。在箱体对称面上锤头正下方一个半径0.05 m的球形区域进行点火，此区域为锤头与金属撞击易产生火花的区域，点火温度为2 000 K(见图3)。

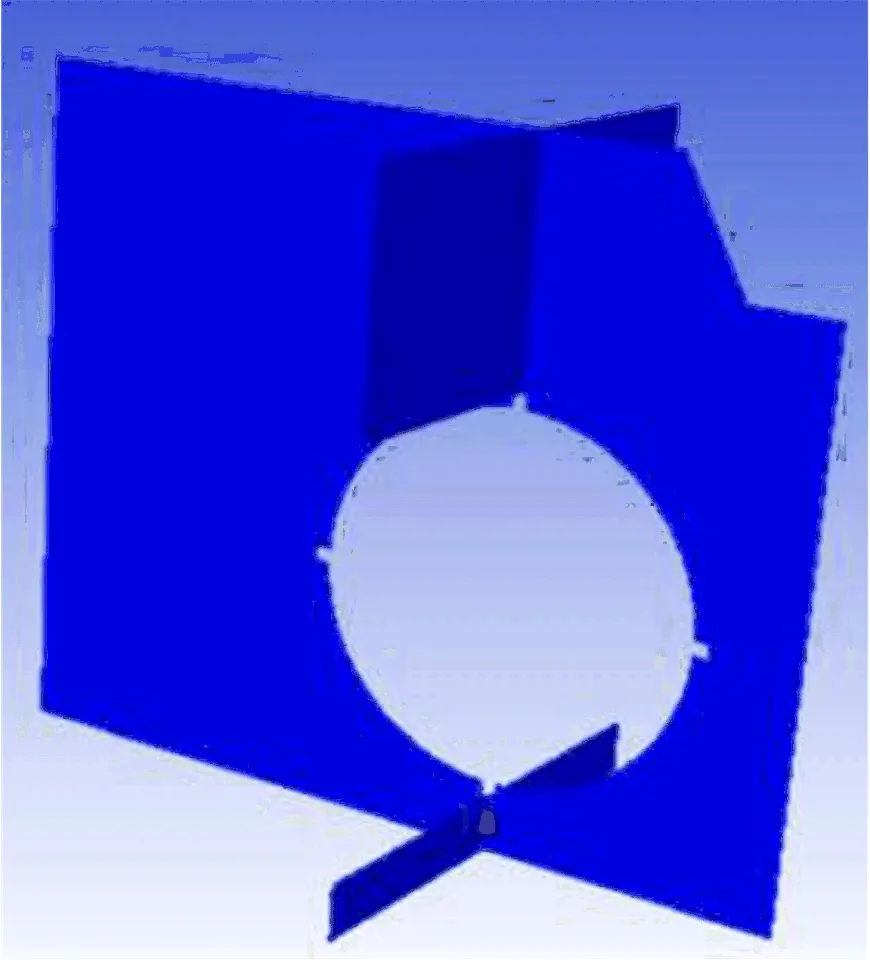
图3 点火条件设置Fig.3 Ignition condition setting

1.2 实验验证

实验装置由配气装置(包括高压甲烷、管道装置、抽真空装置)、测试系统、监控系统、实验样机以及辅助设施组成(见图4)。实验样机基本尺寸为 1 000 mm×750 mm × 1 000 mm，长、宽、高大约为破碎机实体机的四分之一，壁厚25 mm，设计最大承受压力10 MPa，为保证密封性，装配面都采用聚四氟垫片进行密封，实验点火能量取1 J。

图4 实验系统Fig.4 Experimental system

实验样机采用滑移网格模型建模，其模拟结果与实验数据的对比如图5所示，由于数值模拟过程中的环境条件均为理想条件，而实验过程中气体会因为混合均匀度，气体状态以及气密性等不稳定因素产生一定的误差。

图5 仿真与实验对比Fig.5 Comparison of simulation and experiment

从图5中可以看出，在考虑误差的条件下，数值模拟结果与实验结果在压力上升阶段能够较好的吻合，说明滑移网格模型具有一定的可靠性。

2 数值模拟结果与分析

2.1 锤轴转动对爆炸过程压力变化的影响

压力是爆炸的最直观体现，从它的变化可以看出爆炸发生的快慢、强度以及危险性(见图6)。

注：1～6表示转速依次为0、20、40、60、80、100 rad/s图6 爆炸压力上升规律Fig.6 Law of explosion pressure rise

爆炸过程中，破碎机内部的压力整体走势是不断上升的，最终达0.82 MPa左右，破碎机锤轴转动对最终的爆炸压力几乎没有影响。通过拟合得到锤轴转速为0 rad/s与100 rad/s时，压力与爆炸发生时间t(s)的关系为

p0=0.51-0.596t+1.178t2-0.753t3

R2=0.988 02

(1)

p100=0.493-2.543t+20.523t2-24.276t3

R2=0.983 78

(2)

式中：p0、p100分别为锤轴转速0、100 rad/s的压力值，MPa；R2为相关系数。

但是，爆炸结束时间随着锤轴转速的加快而减小，其关系如图7所示。锤轴转速从0 rad/s到40 rad/s时，随着转速加快，到达最大压力的时间缩短较快，缩短速度为0.013 7 s/(rad·s-1)；当锤轴转速从40 rad/s到100 rad/s时，随着转速加快，到达最大压力的时间逐渐缩短变缓，缩短速度约为0.004 125 s/(rad·s-1)，只有0 rad/s到40 rad/s时的三分之一左右；随着转速加快，爆炸结束时间不断缩短，由0 rad/s转速时的1.27 s降至100 rad/s时的0.474 s，降幅约为63%。

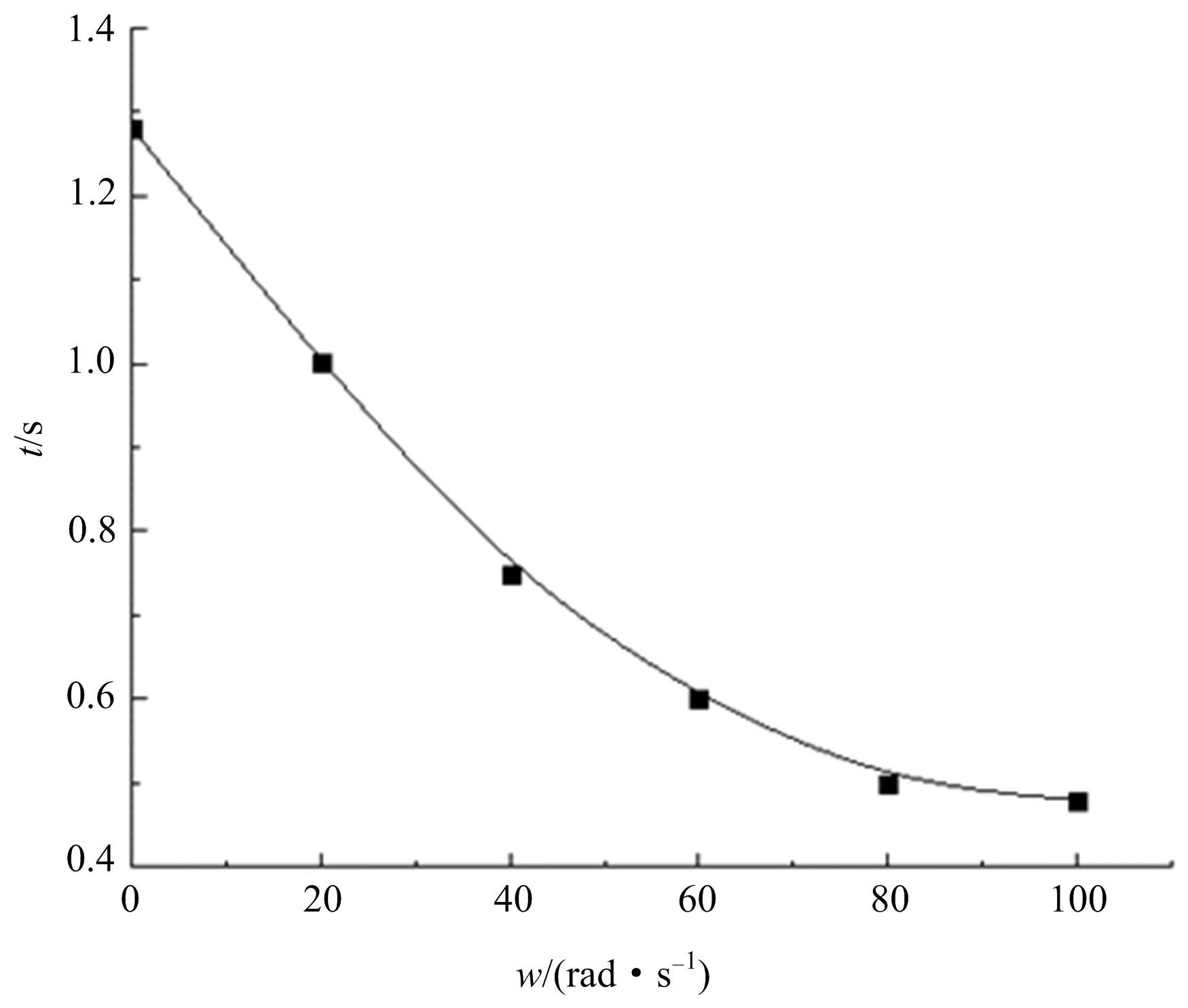
图7 爆炸结束时间Fig.7 End time of explosion

根据压力上升规律得到锤轴在不同转速下的压力上升速率-时间曲线如图8所示。

注：1～6表示转速依次为0、20、40、60、80、100 rad/s图8 压力上升速率Fig.8 Curve of pressure rise rate

以图8中的100 rad/s转速为例，在0 s到0.25 s内，压力上升速率由0 MPa/s迅速升至6.3 MPa/s，由于可燃气体与氧气浓度降低，之后压力速率由6.3 MPa/s迅速下降至0 MPa/s。随着锤轴转速增加，各转速下压力上升速率的峰值逐渐上升，由0 rad/s转速时的1.8 MPa/s升至100 rad/s时的6.3 MPa/s，增加幅度约为3.5倍；当到达压力上升速率的峰值时间不断缩短，由0 rad/s转速时的0.95 s降至100 rad/s时的0.25 s，降幅约为74%。

爆炸发生后，随着锤轴转速的加快，爆炸压力上升越快，完成爆炸的时间越短，增加了爆炸强度与爆炸危险性。

2.2 锤轴转动对火焰扩散的影响

选取箱体对称面作为观测面，锤轴转速100 rad/s时的火焰传播过程如图9所示，点火后的燃烧锋面顺着锤轴的转动方向与锤轴的径向方向开始扩散。沿着锤轴转动方向上，火焰传播角度40 ms时达到50°，70 ms时达到115°，100 ms时达到200°；由于锤轴转动使得火焰出现分块或者不完全连续成块的现象，在40 ms与70 ms时，火焰之间存在间断的连续，100 ms时，火焰已出现分块现象且离开了原来的点火区域。爆炸发生70 ms时的火焰分布如图10所示，火焰沿着锤轴转动方向上的扩散速度随着锤轴转速的加快而加快。

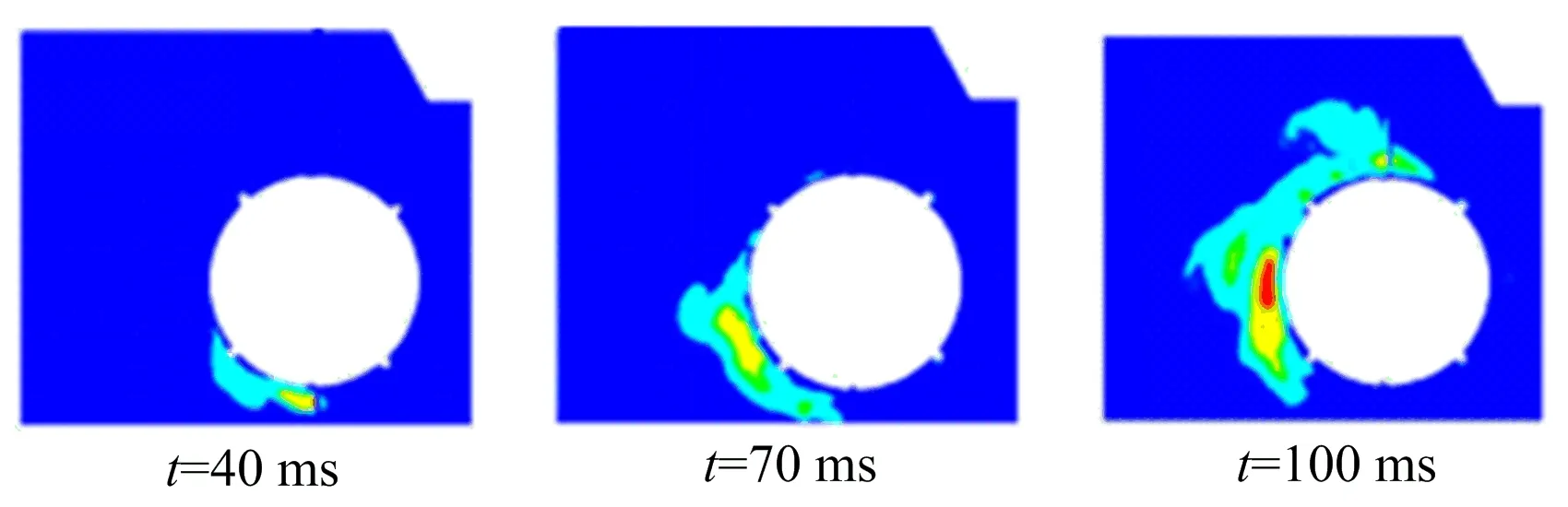
图9 锤轴100 rad/s时观测面上的火焰传播Fig.9 Flame spreading on the observation surface when rotational speed of hammer shaft is 100 rad/s

图10 爆炸发生70 ms后观测面上的火焰分布Fig.10 Flame distribution on observation surface at 70 ms after explosion

火焰传播一周所需要的时间如图11所示。随着锤轴转速的增加，火焰传播一周所需时间逐渐缩短，由0 rad/s转速时的0.771 5 s降至100 rad/s时的0.203 s，降幅约为74%；根据传播一周所需的时间可以得到火焰沿锤轴转动方向上的传播速度(见图12)。通过拟合得到火焰沿锤轴转动方向上的传播速度与锤轴转速的关系。

图11 火焰传播一周时间Fig.11 The time required for the flame to propagate a circumference

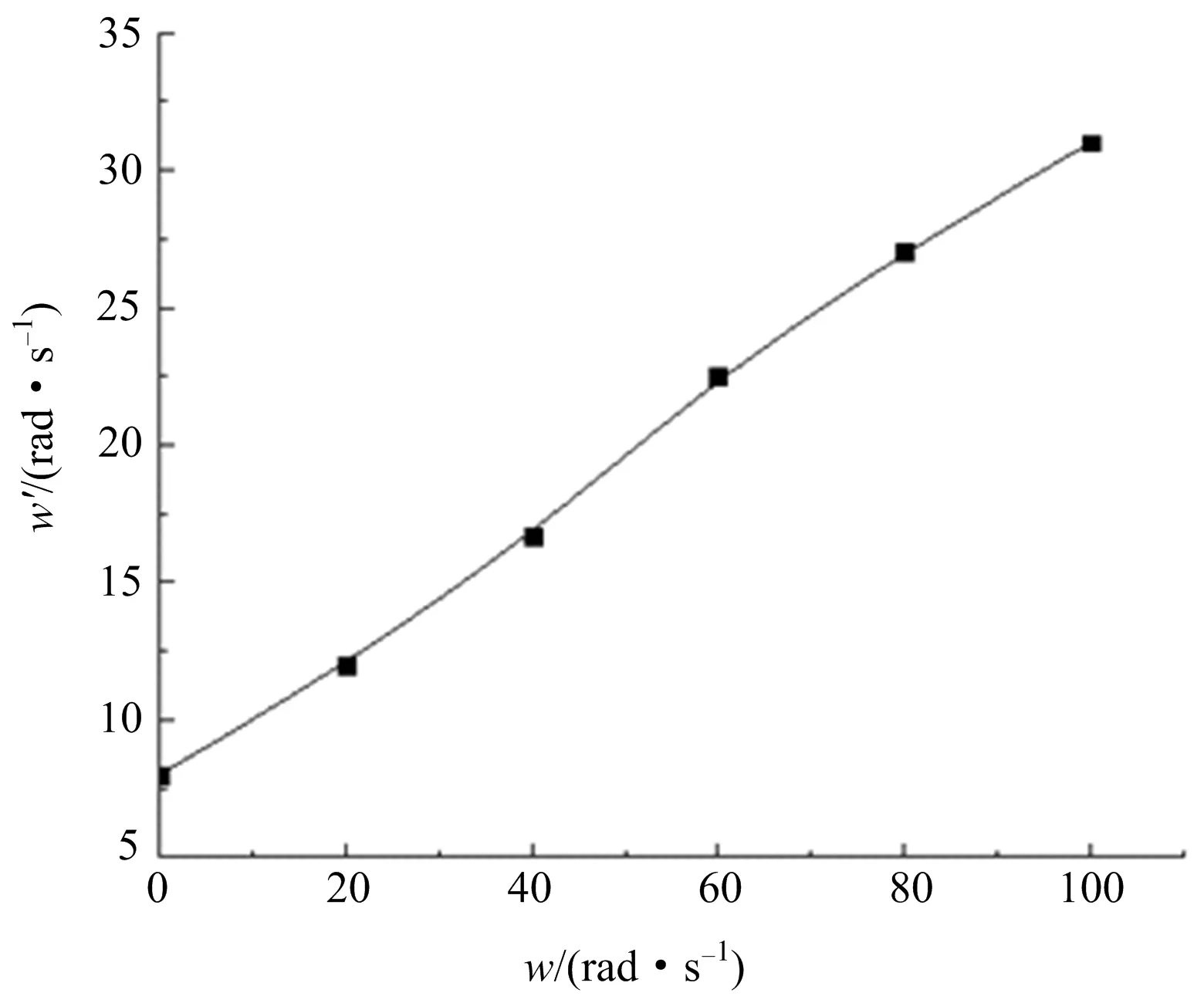
图12 火焰周向传播速度Fig.12 Circumferential propagation velocity of flame

w′=7.741 14+0.237 26wR2=0.995 1

(3)

式中：w′为火焰周向传播速度，rad/s；w为锤轴转速，rad/s；R2为相关系数。

3 结论

1)锤轴转动加快了爆炸的过程。爆炸产生的最大压力不受锤轴转动的影响，但到达最大压力的时间随着转速的增大而减小；随着转速的增大，最大压力上升速率变大，到达最大压力上升速率的时间缩短，爆炸强度与危险性提高。

2)锤轴转动加快了火焰的传播，使得火焰出现分块或者不完全连续成块的现象 。点火后的燃烧锋面顺着锤轴的转动方向与锤轴的径向方向开始扩散，火焰沿锤轴转动方向传播速度与锤轴转速满足线性关系。