融合位置信息的智能驾驶高精地图三维重建
王对武, 邓洪高, 李晓欢, 唐 欣
(1.桂林电子科技大学 信息与通信学院,广西 桂林 541004;2.桂林电子科技大学信息科技学院,广西 桂林 541004)
鉴于此,构建了融合位置信息的道路主干点云提取模型,并结合了道路点云的结构特性,提出了一种融合位置信息和道路结构特性的高精地图三维重建算法,以提高重建效率。
1 应用模型与算法设计
三维地图重建所采集的道路激光点云可分成汽车行驶的道路主干以及非道路主干两部分,应用模型如图1所示。从图1可看出,道路主干包含交通标识牌、路灯杆等具有明显结构特征、分布稀疏的道路元素点云;非道路主干点云结构性较差,甚至不包括智能驾驶所需的道路元素点云,如道路两侧的房屋以及远离道路两侧的非道路基础设施,属冗余数据,将带来三维重建时额外的计算开销。本研究基于位置信息构建道路主干和非道路主干的区分模型,对道路主干进行道路元素点云的提取,以减少重建点云数量。算法流程如图2所示,其基本思想如下:
1)根据位置信息拟合车辆行驶曲线,利用该曲线将点云划分为道路主干的保留区与非道路主干的剔除区,并对道路主干点云进行提取。
2)在道路主干点云中分割并提取道路元素点云,进一步降低待配准点云数据量。
3)利用提取得到的道路元素点云进行配准,获得配准变换矩阵,将原始点云数据进行变换,重建道路三维结构。

图1 应用模型

图2 算法流程图
2 智能驾驶高精地图三维重建方法
2.1 融合位置信息的道路主干点云提取方法
融合位置信息的道路主干点云的提取方法主要包含行车轨迹曲线拟合、曲线的平移以及点云提取3个步骤。在行车轨迹曲线的拟合阶段,首先从位置采集设备中获取车辆的行驶定位数据,将每个定位点记为pose,每个pose包含x、y二维坐标信息。如图1所示,以开始采集的第1个pose为原点,车辆行驶方向为x轴正方向,车辆左侧垂直于x轴的方向为y轴正方向建立平面直角坐标系。pose的x坐标值为车辆相对于原点沿x轴正方向的行驶距离,y坐标值即相对于原点的左右偏移距离。p_1~p_n表示采集到的n个pose,这些pose都存在于行车轨迹曲线path上。车辆在道路中正常行驶的情况下,其行驶轨迹path基本与道路的边沿重合,并与道路的弯曲程度大致相同。因此,可以将其看作道路边沿曲线,并利用此曲线进行道路主干的提取。
相同水灰比的试件,经过冻融0次时的b值最小,经过冻融50次时的b值最高。因此,说明试件经过冻融后强度会降低,但强度对应变率的敏感性会增加,这与熊良宵等[8]获得的结论相同。
为了得到行车轨迹曲线path,采用最小二乘法对pose点集进行曲线拟合。给定函数y=f(x)在点x1,x2,…,xn处的函数值为y1,y2,…,yn,xn与yn为对应的pose数据,n≥3。记所需拟合的行车路径path曲线为p(x)=a0+a1x+…+amxm。在最小二乘法中,为了使得拟合出的p(x)与原始的y=f(x)误差平方和最小,即
(1)
设
S(a0,a1,…,am)=
(2)
对系数a求偏导,并使其等于0,可得
(3)
整理式(3),可得方程组:
(4)
通过全选主元高斯消去法求解式(4),最终得到行驶路径拟合曲线p(x)的系数a0,a1,…,am。
在路径曲线的平移和主干提取中,需要将p(x)平移到包含道路主干的两侧,如图1中的L_left和L_right所示。L_left左侧与L_right右侧2个区域不包含道路主干的点云信息,且由于这2个区域距离LiDAR中心点较远,采集到的点云稀疏且结构性较差,造成数据的冗余。因此,为改善高精地图三维重建效率,需进一步剔除这部分点云数据。
2.2 道路元素点云的配准方法
针对道路主干提取后的点云数据,分析后可发现,道路中的树干和标识牌点云的数据特征明显,其中树干的点云看作柱状,而标识牌则为垂直于地面的立方体。同时,由于道路两侧的树和杆的点云的稀疏性和规律性特点有利于配准,将需要配准的点云分割出道路主干中的树干或标识牌之后,即可采用ICP算法对其进行配准。设有2片分割后的待配准点云数据集S={si|i=1,2,…,m}和D={dj|j=1,2,…,n},其中S表示源点云数据集,D表示目标点云数据集,m、n分别表示2片点云数量,m=n。根据ICP算法,在D中取一点dj,在S点云中,寻找一个与dj欧式距离最近的点si,认为二者为一个对应点对。遍历点云D中的点,即可得到一个对应点集(Sk,Dk),k为对应的点对数量。将2片点云中的点集迭代计算出二者之间的一个旋转平移矩阵参数,即一个空间变换关系。通过这一变化关系,可使得目标点云与旋转后的点云与源点云的对应点之间拥有距离的最小均方差,即目标函数:
(5)
当前后两次迭代的目标函数值之差小于设定的误差阈值ζ,或达到最大迭代次数时,迭代停止,得到旋转平移矩阵参数。
迭代过程如下:
1)在获取的对应点集中分别计算其重心:
(6)
2)由点集Sk、Dk构造协方差矩阵:
(7)
3)由式(7)的协方差矩阵构造4×4的对称矩阵:
(8)
其中:I3为3×3的单位矩阵;Δ=[A23,A31,A12]T;tr(∑(Sk,Dk))为矩阵∑(Sk,Dk)的迹。
4)计算H(∑(Sk,Dk))的特征根和特征向量,最大特征根对应的特征向量就是所求的旋转向量,这里通过四元数qR来表示,然后将四元数旋转向量按式(9)转换为旋转矩阵。
(9)
5)根据求得的旋转矩阵以及重心,即可求得相应的平移向量:
T=μSk-R(qR)μDk。
(10)
根据得到的旋转矩阵与平移向量,将点云D旋转变换到S点云的坐标下,完成点云的匹配。最终通过配准得到结果,对原始点云进行转换配准,完成高精地图三维重建。
3 实验与分析
为了验证本算法的可行性,实验基于开源的KITTI[8]数据集进行验证。KITTI数据集是目前国际上常用的智能驾驶下的计算机视觉算法评测数据集,其内容包含城市、乡村以及高速公路等道路场景采集的真实图像数据。数据集提供的3D点云数据通过64线Velodyne HDL-64E激光雷达以10帧每秒的频率采集,位置信息由OXTS RT3003惯导设备以10 Hz的采集频率获取GPS定位数据。
3.1 融合位置信息的道路主干点云的提取实验
为了保证道路主干的提取完整性,根据我国机动车道宽度标准[9],本实验选取2倍道路宽度作为拟合path后的左右平移量,得出L_left、L_right的曲线函数。将每帧道路三维点云数据中的x数据作为输入,代入L_left、L_right的曲线函数中,将计算所得的yl、yr值与原始的点云数据y坐标值比较。当yl
原始点云和道路主干点云分别如图3、图4所示。对比图3、图4可看出,道路的主干点云被良好地提取出来。

图3 原始点云

图4 道路主干点云
3.2 道路元素提取及重建实验
提取道路主干点云之后,需要对其进行分割,提取主干点云中的树干、标志牌等道路元素点云,并利用这些点云进行ICP算法的配准,得出配准的转换矩阵,最后对原始点云进行转换,得出最终三维重建后的点云图。
针对道路元素的提取,采用区域增长分割算法[10]对道路主干点云进行分割,分割提取的道路元素点云如图5所示。从图5可看出,对应道路主干点云中的树干点云以及标识牌点云被完整地提取出来。
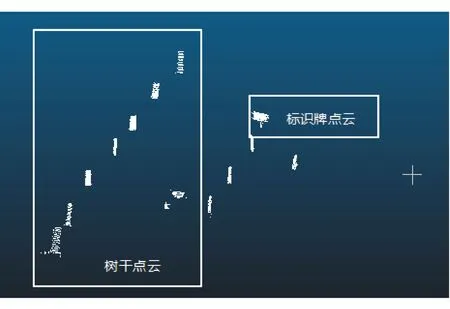
图5 分割提取的道路元素点云
通过对两帧之间提取得到的2片包含道路元素的点云进行ICP配准,并利用配准结果对原始点云进行转换。转换前与转换后的效果图分别如图6、图7所示。

图6 转换前点云
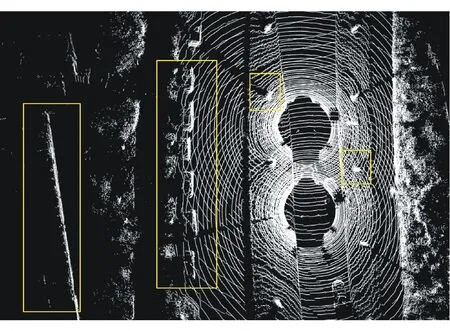
图7 转换后点云
从图6可看出,转换前两帧点云之间的坐标并不一致,能清晰地看到线框内的点云重影。从图7可看出,配准后的对应位置的点云已经重合,实现了坐标的统一,完成了三维重建。
实验采用相同硬件条件下的点云配准计算时间作为对比参数,将使用ICP配准的三维重建算法与本算法进行比较,对比结果如表1所示。随着迭代次数的递增,2种方法重建耗时都随之增加,但本算法的点云配准计算时间远小于ICP算法,说明提取道路主干点云及道路元素点云有利于减少点云配准时间,提高地图三维重建的效率。

表1 算法性能对比 ms
4 结束语
针对常用高精地图三维重建中点云数据量大、初始值不稳定且未考虑采集的点云结构对重建效率的影响的问题,提出了一种融合位置信息的智能驾驶高精地图三维重建算法。该算法结合道路点云的结构特性,构建了融合位置信息的道路主干点云提取模型,将道路点云划分为道路主干与非道路主干区域,并对道路主干点云进行道路元素点云的提取,减少了高精地图三维重建点云数量,降低了点云配准的计算量。最后基于开源的KITTI Dataset数据集验证结果表明,相较于使用ICP配准的三维重建算法,本算法用时更短,能更高效地实现高精地图三维重建。

