六面体可展机构自由度与运动特性分析
刘文兰 马鹏飞 闵 为 许允斗 郭金伟 赵永生
(1.兰州理工大学能源与动力工程学院, 兰州 730050; 2.燕山大学河北省并联机器人与机电系统实验室, 秦皇岛 066004)
0 引言
作为空间可展机构中的一类,多面体可展机构结构设计和分析是目前研究热点之一[1-7]。多面体可展机构的运动链间存在耦合,目前国际上尚未形成多环耦合机构系统的自由度分析理论。AGRAWAL等[8]用移动副代替多面体边线设计了多种单自由度多面体可展机构,基于Grübler-Kutzbach公式(简称G-K公式)分析了这种仅含移动副的多面体机构的自由度,但采用G-K公式计算一般多面体机构的自由度时,机构阶的求解存在较大困难。文献[9-11]基于PRRP运动链和一种对称8杆机构综合了一系列具有径向往复运动的过约束可展多面体机构,并根据机构所含关节数和约束矩阵的秩之间的关系,分析了多面体机构的自由度,但是当机构中关节较多时,求解高阶约束矩阵的秩难度较大。杨毅等[12]基于单闭环7杆机构提出了一种四棱锥可展机构,并将其拆分为一个三闭环机构和一个二连杆运动链,通过分析三闭环机构得到了四棱锥机构的自由度,但并不是所有的多面体机构都能拆分为一个与原机构自由度等价的机构和一个只引入虚约束的运动单链。文献[13-15]研究了Hoberman魔球机构的自由度和运动特性。许允斗等[16]针对一种四面体可展机构的自由度问题,提出了一种拆杆等效法,该四面体机构耦合度较低,拆除一个串联运动链后的机构恰好可看作并联机构,当机构耦合度更高时,此方法是否可行未作进一步说明。文献[17-18]分别采用拆分杆组法和拓展多面体框架的自由度分析方法,分析了一种六面体可展机构的自由度。刘婧芳等[19-20]提出了多环耦合机构自由度分析的等效法和独立运动分流标记法,并应用于一种类正四面体机构[21]和二十面体可展机构[22]中。文献[23]采用独立运动分流标记法分析了一种六面体可展机构的自由度。这两种方法中独立运动单元的拆分是关键,若原机构耦合度较高,拆分的独立运动单元仍为多环耦合运动链时,其等效串联链的建立是个难点。此外,WOHLHART[24-26]也对多面体可展机构的构型、运动分析等展开了研究。
本文在文献[16]的基础上,以一种多环耦合六面体机构[17-18,23]为研究对象,提出一种自由度分析方法。先将机构中部分耦合运动链视作动平台,基于螺旋理论建立动平台的等效串联支撑分支;然后逐渐释放动平台中的构件,建立变化后动平台的等效串联分支;最后构建仅由一个连杆组成的等效并联机构,进而采用并联机构自由度分析方法得到原多面体机构的自由度。借助仿真软件验证六面体机构自由度理论分析结果的正确性,并分析该机构的运动特性和折叠比。
1 结构及自由度分析
1.1 结构简介
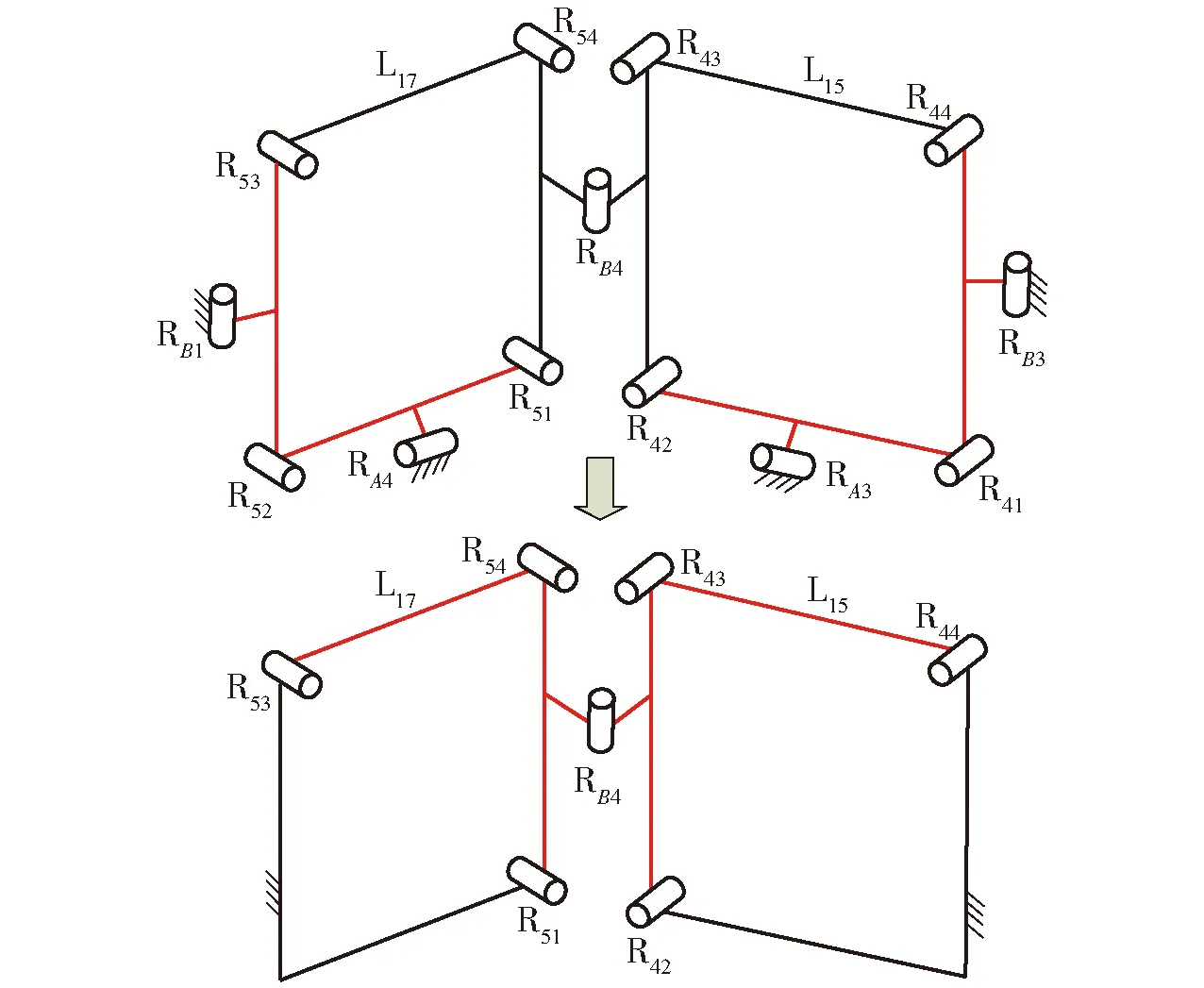
图1为完全相同的24个连杆(记作L1~L24)和36个转动副(R)组成的一种六面体机构[17-18,23],其第i(i=1,2,…,6)个面上的4个转动副Ri1、Ri2、Ri3和Ri4轴线相互平行且垂直于该平面,连接相邻两面的转动副轴线平行于两平面的交线, 六面体各顶点处3个转动副轴线相交于一点,记为oj(j=1, 2, …, 8)。该机构具有对称结构,选取连杆L1为机架,在顶点o1建立参考坐标系o1xyz,其中,x轴与转动副RA1的轴线重合,z轴与转动副R12的轴线重合,y轴根据右手定则确定。

图1 六面体机构Fig.1 Hexahedral mechanism
1.2 自由度分析
图1为六面体机构结构简图,若将任意1个连杆(不含机架杆L1)视作动平台,则连接动平台和机架的支撑分支间耦合关系错综复杂,对该六面体机构进行自由度分析难度较大。本文先将N1(1 图2为六面体机构的自由度分析流程,具体分析过程如下: 选取四连杆机构R21R22R23R24、R61R62R63R64和R41R42R43R44依次通过转动副RC1和RC3串联而成的运动链整体为动平台1,如图3所示。动平台1又通过转动副RA1、RB1、RB2、RB3、RB4、RC2、RC4和RA3与机构剩余部分相连,故动平台1与机架杆L1之间存在8个支撑分支。 图2 六面体机构自由度分析流程Fig.2 DOF analysis procedure of hexahedral mechanism 图3 动平台1Fig.3 Moving platform No.1 图4 拆除动平台1后的运动链Fig.4 Part of dismantling moving platform No.1 但动平台1的8个分支之间存在耦合链,为便于建立动平台1的8个运动等效串联分支,先将动平台1从原机构中拆除,剩余部分如图4所示。在图4中,与转动副RA1、RB1、RB2、RB3、RB4、RC2、RC4和RA3相连的杆件分别为机架L1、连杆L20、L9、L11、L18、L10、L17和L3,基于螺旋理论分别分析这些连杆相对于机架的自由度数目和性质,从而建立其与机架之间的等效串联运动链,如表1所示。 表1 连杆L9、L10、L11、L20、L17、L18、L3与机架之间的等效串联链 表1中 Pe1为轴线与转动副R31和连杆L9的中心轴线均垂直的移动副,Pe2为轴线与转动副R52和连杆L20的中心轴线均垂直的移动副,Pe3为轴线与转动副R12和连杆L2的中心轴线均垂直的移动副。表1中等效串联链结合转动副RA1、RB1、RB2、RB3、RB4、RC2、RC4和RA3可得动平台1的8个运动等效串联分支分别为RA1、R11RA4R52RB1、R12RA2R31RB2、R12RA2R32RB3、R11RA4R51RB4、R12RA2Pe1RC2、R11RA4Pe2RC4和Pe3RA3。动平台1、机架及8个等效串联分支构成的并联机构如图5所示。 图5 动平台1、机架以及8个等效串联分支构成的并联机构Fig.5 PM composed of moving platform No.1, base and eight equivalent series limbs 图5的机构又可视作以四连杆闭环机构R61R62R63R64整体为动平台2、含4个支撑分支的并联机构,其中,分支1和分支2如图6所示,分支3和分支4分别为动平台1的等效串联分支RC2Pe1RA2R12和RC4Pe2RA4R11。 图6 动平台2的分支1和分支2Fig.6 Two limbs of moving platform No.2 图7 动平台2的分支1拓扑结构Fig.7 Topological structure of the first limb of moving platform No.2 从图6可以看到,分支1和分支2亦属于空间多闭环耦合机构,图7给出了分支1的拓扑关系,分支2的拓扑关系与分支1的类似。为建立分支1的等效串联分支,先分析分支1中连杆L7相对于机架的自由度。连杆L7与机架相连的两个支链之间存在耦合,基于螺旋理论分析连杆L6和L8受到的约束螺旋系可得其与机架之间的运动等效串联链分别为R21RA1和R22RA1,进而可得连杆L7的两个独立运动等效串联支链为R24R21RA1和R23R22RA1。求等效串联支链R24R21RA1和R23R22RA1施加给连杆L7的约束螺旋系的反螺旋,可得在参考坐标系o1xyz下表示的连杆L7的运动螺旋系为 (1) 式中 (l1,m1,n1)——点o5在坐标系o1xyz中的坐标 式(1)表明连杆L7具有与转动副R22的轴线和直线o1o5均垂直方向的移动自由度和绕转动副RA1轴线的转动自由度,从而可得图6中分支1的运动等效串联分支为RC1Pe4RA1,其中,Pe4表示轴线与转动副R22的轴线和直线o1o5均垂直的移动副。 同理,可得动平台2的分支2中连杆L15的运动螺旋系为 (2) 式中 (l2,m2,0)——点o2在坐标系o1xyz中的坐标 综上可得动平台2、机架、等效串联分支RC1Pe4RA1和RC3Pe5RA3Pe3、分支3以及分支4组成的并联机构,如图8所示。 图8 动平台2、机架和4个等效串联分支组成的并联机构Fig.8 PM composed of moving platform No.2, base and four equivalent series limbs 在图8的机构中,把连杆L22视作动平台3,其上有3个转动副,分别为RC2、R62和R63,故动平台3通过3个分支与机架L1相连。一个分支为独立串联分支RC2Pe1RA2R12,另外两个分支间存在耦合。基于螺旋理论可推得另外两个耦合分支的运动等效串联分支为R62Pe4Pe6和R63Pe4Pe6,其中,Pe6表示轴线与转动副R22轴线平行的移动副。因此,动平台3、机架、分支RC2Pe1RA2R12、分支R62Pe4Pe6和分支R63Pe4Pe6组成一个含三分支的并联机构。 求等效串联分支RC2Pe1RA2R12、R62Pe4Pe6和R63Pe4Pe6施加给连杆L22的约束螺旋系的反螺旋,可得连杆L22的运动螺旋系为 (3) 式(3)表明连杆L22具有3个自由度,分别为绕z轴的转动和与转动副RB2轴线垂直的两个移动自由度,从而可得原六面体机构的自由度为3,与文献[17-18,23]结论一致。 六面体机构在一般位形下(图1),每个面上的4个转动副Ri1~Ri4的轴线始终相互平行且垂直于该平面,相邻两个面之间的转动副轴线平行于两个面的交线,每个顶点处的3个转动副轴线相交于一点,即所有转动副的相对位置和方向与上述分析位形下的相同。因此,该六面体可展机构的3个自由度具有全周性。 当机构输入数目与机构自由度数目相等时,机构一般可实现确定的运动,但对自由度大于2的多自由度机构来说,即使输入数目与机构自由度数目相等,若驱动副选择不合适,机构也会发生输入干涉[27]。根据上文分析可知,图1所示六面体机构具有3个自由度,故需要添加3个独立的驱动使其实现确定的运动。该六面体机构的每个面由4个连杆和4个轴线相互平行的转动副组成,如图9所示,显然,该平面四杆机构具有1个自由度。此外,由于六面体机构的结构对称性,相对的两平面四杆机构始终具有相同的运动。因此,3个独立的驱动副应分别在相邻的3个平面四杆机构或位于六面体边线并交于同一顶点的3个转动副中选择。 图9 平面四杆机构简图Fig.9 Schematic of planar four-bar mechanism 选取转动副R12、R22和R31为驱动副,采用文献[27]中多自由度并联机构的输入选取准则,检验转动副R12、R22和R31为驱动副的合理性。 假设将转动副R12、R22和R31刚化,六面体机构中平面四杆机构R11R12R13R14、R21R22R23R24和R31R32R33R34将失去自由度,原六面体机构变为图10所示机构。将图10中闭环运动链R61R62R63R64整体视作动平台,其通过转动副RC1、RC2、RC3和RC4最终与机架相连。连杆L5、L6、L7、L8整体通过转动副RA1与机架相连,通过转动副RB2与连杆L9相连,而连杆L9、L10、L11、L12整体又通过转动副RA2与机架相连,根据三角形的稳定性可知,其形成的含3个转动副的闭环运动链不具有自由度。因此,动平台R61R62R63R64通过转动副RC1和RC2与机架相连的等效串联分支分别为RC1和RC2,其余2个分支结构如图11所示。 图10 刚化驱动副后的六面体机构结构示意图Fig.10 Schematic of hexahedral mechanism after fixing driving joints 基于图2的自由度分析,可得图11中连杆L15和连杆L17相对于机架的自由度为零,则动平台R61R62R63R64通过转动副RC3和RC4与机架相连的等效串联分支分别为RC3和RC4,从而可得动平台R61R62R63R64和其4个等效串联分支以及机架构成的并联机构如图12所示。 图11 动平台R61R62R63R64的另外两个分支结构简图Fig.11 Schematic of two other limbs of moving platform R61R62R63R64 图12 动平台R61R62R63R64、4个等效串联分支和机架组成的并联机构Fig.12 PM composed of moving platform R61R62R63R64, base and four equivalent series limbs 图12的多闭环机构中,独立的平面四杆机构R61R62R63R64具有1个自由度,当其4个连杆分别通过转动副RC1、RC2、RC3和RC4与机架相连时,每个转动副提供的3个约束力和2个约束力偶限制了原平面四杆机构R61R62R63R64的自由度。因此,图12的等效机构自由度为零,从而可得刚化驱动副R12、R22和R31后六面体机构自由度为零,则根据文献[27]中多自由度并联机构的输入选取准则,可以选取六面体机构的转动副R12、R22和R31作为3个驱动副。需要注意,转动副R12、R22和R31并不是该六面体机构驱动副的唯一选择。 建立六面体机构的仿真模型如图13所示,驱动副R12、R22和R31的角位移分别为θ1、θ2和θ3,根据该六面体机构的结构对称性,取0°≤θk≤90°(k=1, 2, 3)分析其运动特性。 给转动副R12、R22和R31施加相同的驱动:θ1=θ2=θ3=(90-5t)°,其中,t表示时间。仿真10 s,测得机构运动过程中转动副的角位移如图14所示。改变转动副R12、R22和R31的驱动值:θ1=(90-4t)°、θ2=(90-5t)°、θ3=(90-6t)°。仿真10 s,测得机构运动过程中转动副的角位移如图15所示。 图13 六面体机构的仿真模型Fig.13 Simulation model of hexahedral mechanism 图14 相同驱动下机构各转动副的角位移Fig.14 Angular displacements of joints of hexahedral mechanism under the same actuations 图15 不同驱动下机构各转动副的角位移Fig.15 Angular displacements of joints of hexahedral mechanism under different actuations 图14表明当六面体机构的3个驱动相同时,6个平面四杆机构中的转动副具有相同的运动,位于机构12条边线上的转动副具有相同的运动,即机构在任意位形下其6个面形状完全相同。图15表明六面体机构在3个不同大小驱动下,相对的两平面四杆机构中转动副始终具有相同的角位移,位于六面体相互平行棱边的转动副角位移相同,即机构在任意位形下相对的两个面形状相同,此仿真结果与理论分析相吻合。 六面体机构在不同驱动下的位形变化如图16所示,从图16可看到,六面体机构在θ1=θ2=θ3=90°时呈现出正方体,在0°<θ1、θ2、θ3<90°时呈现出平行六面体,由于每个杆长恒定,故该六面体机构在正方体状态的包络体积大于平行六面体状态的包络体积。因连杆间的干涉问题,六面体机构实际中只能无限接近图14中的3种极限位形:(θ1=0°,θ2=θ3=90°)、(θ2=θ3=45°,θ1=90°)和(θ1=θ2=θ3=0°),为了便于讨论六面体机构的最小包络体积,表2列出了几种极限位形下六面体机构的包络体积及驱动角。 图16 六面体机构在不同驱动下的位形变化Fig.16 Configuration changes of hexahedral mechanism under different actuations 将六面体机构在整个运动空间中的最大包络体积与最小包络体积之比定义为该机构的折叠比,计算式为 (4) 式中η——机构折叠比 Vmax——六面体机构的最大包络体积 Vmin——六面体机构的最小包络体积 a——θ1=θ2=θ3=90°时六面体机构的包络正方体边长 h——θ1=θ2=θ3=0°时六面体机构的包络圆柱的高 d——θ1=θ2=θ3=0°时六面体机构的包络圆柱的底面圆直径考虑机构的真实尺寸,因连杆间的干涉问题六面体机构的实际折叠比小于12.294 7。 表2 六面体机构的包络体积及对应驱动角 (1)对一种六面体可展机构的自由度进行了分析。基于拆杆、等效、复原的思想,不断选取机构动平台,建立运动等效机构,逐渐降低原机构的耦合度,最终基于并联机构自由度分析理论得到了六面体机构的自由度。 (2)分析了六面体可展机构的运动规律。机构中相对的两平面四杆机构始终具有相同的运动,位于机构平行棱边上的转动副具有相同的角位移。 (3)分析了六面体机构的折叠性能。六面体可展机构在不同组合的驱动下可实现多种位形,具有较大的折叠比,可适用于不同任务、不同需求的场合。


Tab.1 Equivalent series chains between base and linksL9, L10, L11, L20, L17, L18and L3













2 运动特性
2.1 驱动副选取



2.2 仿真分析



3 折叠性能

Tab.2 Envelope volume and corresponding drivingvalues of hexahedral mechanism
4 结论

