高温环境下薄壁试件随机振动疲劳研究
王建,沙云东,杜英杰,胡翼飞,张伟瑞
(1.成都航空职业技术学院 航空工程学院,成都 610100;
2.沈阳航空航天大学 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136)
振动疲劳现象普遍存在于航空航天薄壁结构之中,如航空发动机火焰筒隔热防振屏冲压式发动机尾喷管超音速飞行器的外部蒙皮等。这些薄壁结构在工作中除了承受机械振动载荷气动载荷强声载荷外,还处在严峻的高温载荷环境下[1]。当外界载荷的频率范围与薄壁结构的固有频率重合或接近时,薄壁结构将会发生共振现象。这种复杂环境下的共振将会严重影响薄壁结构的力学特性,并在其内部形成高幅值的动力学响应,从而在薄壁结构的某些部位产生疲劳裂纹[2],形成巨大的安全隐患。因此,高温环境下薄壁结构的随机振动疲劳成为国内外研究学者共同的问题。
国外关于振动疲劳问题的研究起步较早,其研究成果已经运用到航空结构件的设计手册与强度设计标准中[3],如美国的军用标准《飞机强度和刚度》[4],马歇尔太空飞行中心(George C. Marshall Space Flight Center)的强度设计文件[5]等。其中,基于内时理论,Valanis[6]研究了疲劳寿命与载荷频率的关系。Whaley[7]等利用不可逆过程热力学原理对振动疲劳进行了探讨。Sanliturk[8]提出了一种基于频率响应函数的振动疲劳寿命分析方法,不仅研究了结构弹性对疲劳寿命的作用,而且分析了结构惯性和阻尼对疲劳寿命的影响。Bishop[9]采用功率谱密度函数对结构的随机振动疲劳寿命进行了预测。近代以来,Hanna[10]通过有限元法,在频域内进行了电子控制元件的振动疲劳寿命预估与分析。此外,Liu[11]Kim[12]和Selverlan[13]等研究人员从不同的角度出发,对结构振动疲劳寿命预测开展了相应的理论分析与探讨。虽然国内关于结构振动疲劳问题研究起步较晚,但已在此方面取得了较多的研究成果[14]。其中,姚起杭给出了结构振动疲劳的工程分析方法和结构设计技术[15-16]。金奕山针对宽带随机振动载荷下结构疲劳寿命预测,进行了大量的理论推导与分析[17]。沙云东教授[18-19]针对航空发动机火焰筒在热声环境下的振动疲劳问题,开展了大量的课题研究,并基于改进的雨流计数法,对薄壁结构的疲劳寿命进行了预估。
考虑到高温环境下薄壁结构随机振动试验的经费高昂,国内外的研究大都止步于常温下的随机振动试验或数值仿真类的基础性研究,这使得理论与实际得不到较好的验证。文中首先对国内外关于结构随机振动疲劳的研究现状展开相应的的综述总结,然后实施高温环境下薄壁试件的随机振动试验,获取振动响应结果与危险点位置的疲劳寿命,并基于数值仿真完成薄壁试件的响应计算分析与寿命预测。最后将仿真结果与试验结果进行比对,验证仿真计算方法的有效性。研究结果将为航空航天薄壁结构的动强度学设计与疲劳寿命预测提供一定的参考依据。
1 振动疲劳概述
依据外界载荷的频率范围与结构的固有频率是否重合或接近,振动疲劳可以分为共振疲劳和非共振疲劳两大类。根据实际结构的共振特点,主要分为整体共振部件共振局部共振三类。
共振疲劳所涉及的主要是部件共振和局部共振。结构处于复杂的载荷环境下,将出现振动现象,从而引发结构在一定频率范围内的振动响应。这种响应的频率与外界载荷的频率相接近或重合时,将在结构的应力集中位置或者具有缺陷的位置出现高幅值动力学响应的共振疲劳现象。在这个过程中,结构的阻尼大小和外界载荷的幅值情况将会直接影响结构的动力学响应幅值。因此,中等量级的外界载荷将对结构的共振疲劳失效起到主要作用。非共振疲劳是指外界载荷频率远离结构共振频率,一般存在于单频振动激励或者结构刚度较大而外载频率较低的振动过程。在这个过程中,结构的动力学响应幅值由外载的大小结构的质量强度刚度和阻尼等共同影响。因此,少量较大量级的激励将对结构的非共振疲劳失效起主要影响作用。
1.1 振动载荷建立
随着结构可靠性要求的提高,进行试验件可靠性寿命评估成为国内外研究的难点。如果按照以往的振动疲劳试验方法来开展相应的试验工作将严重影响工程进度及科研人员的研究效率。当今科学技术迅猛发展,产品更新换代的速度加快,这就要求科研工作者要在较短的时间内完成振动疲劳寿命评估的工作。因此,如何加速设计振动疲劳试验成为科研工作者的研究重点。关于载荷谱的加速编辑处理主要在时域和频域内进行。
时域疲劳载荷谱编辑技术主要包含:峰谷值抽取方法设置SWT(Smith-Watson-Topper)损伤门槛值技术时间关联编辑技术频率关联编辑技术设置循环幅度门槛值和基于损伤的直方图编辑等。还有一些信号处理方法也可用于编辑载荷谱,例如减少采样点,删小量法等。为准确获取载荷序列中等效的损伤信息,需要有合适的计数方法对所测得的载荷信号进行处理。Matsuishi 和Endo[20]引入了雨流计数算法,从时间序列载荷中获取程序块载荷谱。载荷循环通过幅值均值和循环数目表示出来。Bannantine 和Amzallag[21]发展了该算法的三点和四点形式。雨流循环计数法示例如图1 所示,相应的计数结果见表1。
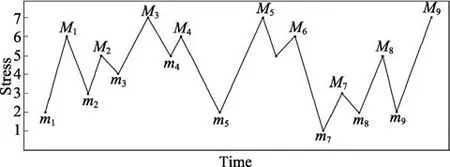
图1 雨流循环计数示例

表1 雨流循环计数结果
1.2 振动疲劳试验的研究
国内周凌波[22]通过开展航空典型结构件的随机振动疲劳寿命分析,完成了铝合金结构件的随机振动疲劳试验设计,并依次进行了模态分析试验宽带随机振动疲劳试验有限元仿真分析仿真与试验的比对。其振动疲劳试验的测试系统主要包含激励系统控制系统采集系统和显示记录系统,涉及到的设备主要包括激励设备传感器设备采集设备显示记录设备和数据分析设备,如图2 所示。周凌波所采用的振动疲劳试验方法也是现阶段国内外所通用的一种试验方法。
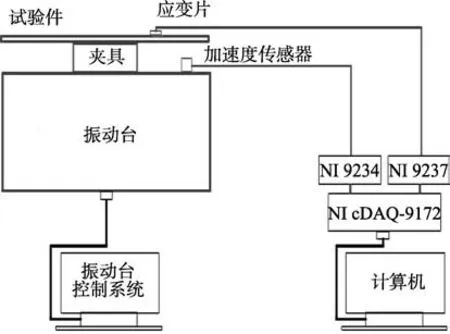
图2 振动疲劳试验原理
2 薄壁试件随机振动疲劳研究
为了研究高温环境下薄壁试件的随机振动疲劳,文中选取薄壁试验件为研究对象,厚度为1.5 mm,如图3 所示,其材料参数见表2。通过有限元仿真完成该试验件的模态计算危险位置分析及动力应力计算,并基于改进的雨流循环计数法,结合Morrow 平均应力模型和Miner 线性累计损伤理论,完成危险位置的寿命预估。最后完成薄壁试件在高温环境下的振动疲劳试验,将试验结果与仿真结果进行比对,验证计算方法的有效性。其中,在仿真和试验中均对试验件根部位置进行固支约束,并以功率谱密度的形式施加振动量级在2.0g~4.0g 之间的振动载荷,温度范围为25~600 ℃。

图3 几何模型

表2 试验件材料参数
2.1 仿真计算与分析
通过施加振动量级为2.0g 的振动载荷,计算了薄壁件在25~600 ℃温度范围内的前两阶固有频率,见表3。可以看出,前两阶固有频率随温度的增加而下降,这是因为结构在屈曲前随温度的增加出现了软化现象。薄壁件在数值仿真下的应力云图如图4 所示,分析发现,在高温载荷和随机振动载荷作用下,结构的约束位置和形状突变位置出现应力集中现象,根部和颈部的应力较大,容易对结构产生破坏。

表3 前两阶固有频率 Hz
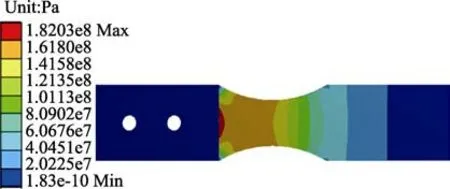
图4 试验件在数值仿真下的应力云图Fig.4 Test pieces stress distribution nephogramof mathematical simulation
2.1.1 动应力响应分析
计算发现,不论在何种载荷条件下,危险点位置x 方向的应力远大于其他方向。因此,主要对x 方向的应力进行分析与比对。在室温条件下,振动量级由2.0g 增至4.0g 时,结构基频处响应峰值由1.86×1015Pa2/Hz 增至7.41×1015Pa2/Hz。第二阶固有频率处的响应峰值由8.27×1012Pa2/Hz 增至3.31×1013Pa2/Hz,其值弱于基频处的响应幅值。因为温度不变时,结构模态频率不变,故响应峰值没有出现偏移现象,如图5a 所示。在振动量级为2.0g 条件下,温度由25 ℃增至600 ℃时,结构基频处响应峰值由1.85×1015Pa2/Hz 增至7.41×1015Pa2/Hz,如图5b 所示。第二阶固有频率处的响应峰值由 8.27×1012Pa2/Hz 增至1.19×1013Pa2/Hz,其值弱于基频处的响应幅值。
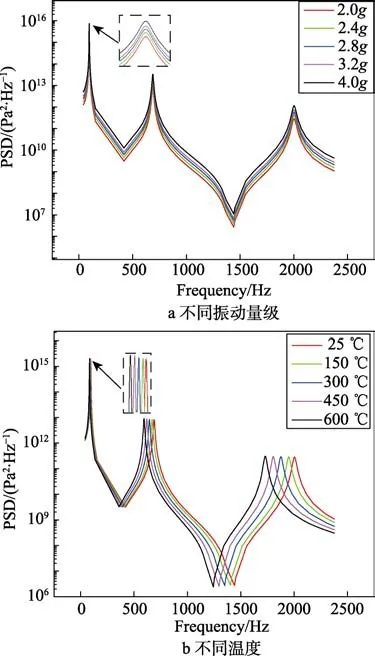
图5 x 向应力功率谱密度
2.1.2 疲劳寿命分析
振动量级由2.0g 增至4.0g 时,结构危险位置的疲劳寿命呈抛物线趋势降低,温度不同,但变化趋势一致,如图6 所示。温度由25 ℃增至600 ℃时,结构危险位置的疲劳寿命呈加速降低的趋势,振动量级不同,但变化趋势一致,如图7 所示。

图6 不同振动量级下疲劳寿命

图7 不同温度下疲劳寿命
2.2 试验研究与比对
通过开展薄壁试验件在高温环境下的振动疲劳试验,获取结构的危险位置与疲劳寿命,试验件安装如图9 所示。可以看出,试验件的疲劳裂纹出现在根部和颈部位置,如图10 所示。试验数据与仿真数据的比对结果见表4,主要包含轴向动应力疲劳寿命和应力响应峰值频率。分析发现,应力响应水平基本保持一致,疲劳寿命量级相当,基频误差较小。对比结果验证了高温环境下薄壁试件随机振动疲劳仿真法的有效性与可靠性。
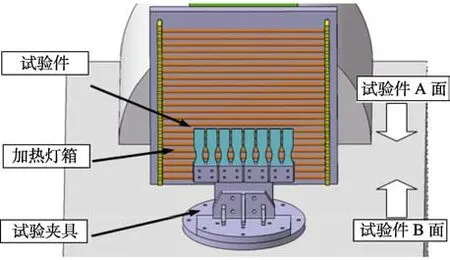
图8 随机振动疲劳试验件及夹具安装

图9 高温随机振动试验后试验件破坏的结果
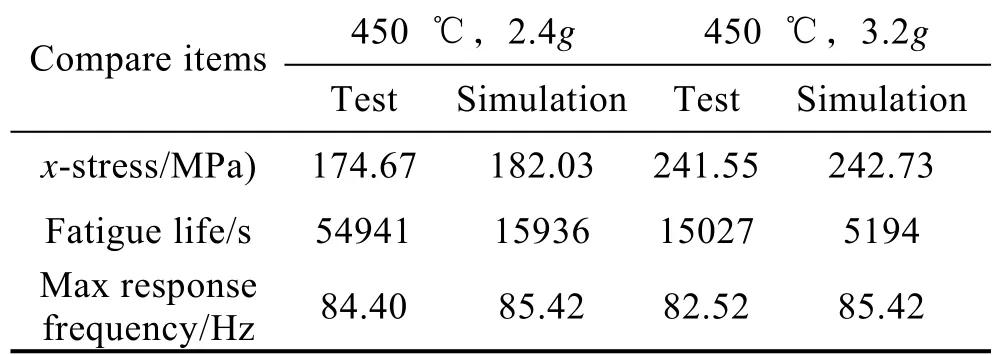
表4 随机振动试验与仿真结果
3 结论
文中通过对国内外随机振动疲劳问题的检索与分析,从振动载荷的建立与振动疲劳试验两个方面进行了较为全面的综述。此外,选取金属薄壁件为研究对象,开展了高温环境下薄壁试件的随机振动疲劳研究,并从仿真计算与分析振动疲劳试验测试对比验证三个方面进行了详细的分析,得出以下结论。
1)屈曲前,随着温度的增加,结构出现软化现象,基频呈降低趋势。
2)高温强振动环境下,结构的危险位置主要出现在固支边界或形状突变位置。
3)基频处的动力学响应峰值是结构疲劳寿命的主要影响因素。
4)危险位置的疲劳寿命随温度和振动量级的增加呈抛物线降低趋势。
5)通过仿真与试验的比对,验证了高温环境下薄壁试件随机振动疲劳仿真计算方法的有效性与可靠性。

