基于遗传-蚁群融合算法的共享单车优化调度研究

梁岩 王靓 李林玉 徐小本

摘 要：随着共享单车规模的扩大，资源调配需要更加科学合理。因此，提出了一种基于遗传-蚁群融合算法的共享交通工具调度方法。对比该调度方法和常规蚁群算法，两种算法的结果一致，且融合算法的收敛速度更快。

关键词：共享单车;优化调度;遗传-蚁群融合算法;数学模型

中图分类号：U491.2+25 文献标识码：A 文章编号：1003-5168（2019）01-0105-02

Research on Optimal Scheduling Problem of Shared Single Vehicle Based

on Ghybrid Genetic Algorithm- Ant Colony Optimization

LIANG Yan WANG Liang LI Linyu XU Xiaoben

（Zhengzhou University，Zhengzhou Henan 450000）

Abstract： With the expansion of the scale of shared bicycles， resource allocation needs to be more scientific and reasonable. Therefore， a method of shared transportation scheduling based on genetic and ant colony fusion algorithm was proposed. The comparison between this scheduling method and the conventional ant colony algorithm showed that the results of the two algorithms were the same， and the convergence of the scheduling results of the fusion algorithm was faster.

Keywords： shared bikes;scheduling methods;genetic-ant colony fusion algorithm;mathematicle model

随着契合互联网思维的ofo和Mobike进入市场，兴起了无桩自行车。与站点式共享自行车相比，无站式共享自行车节省了启动成本，但用户的随机使用行为带来了分布不平衡，降低了共享自行车系统的便捷性。本文基于具有正反馈性的蚁群算法，借鉴遗传算法，提出了一种遗传-蚁群融合算法，提高了算法的收敛性。该方法以最小距离成本为最终目标，适用于大中规模的共享自行车系统。

1 基本思路

本文提出了一种基于静态调度的三步优化调度方法。首先，采用K-means算法对自行车聚类并集群修复。其次，采用遗传算法获得连接各节点的初始解，并采用蚁群算法计算和做出装卸载自行车數量的决策。最后，直接使用蚁群算法获得连接每个集群内站点的最短路径，完成集群内部小范围的调度。

2 站点的聚类

聚类修复是调度车辆访问一次即可达到各站点自行车的平衡，避免二次及多次访问，主要包括分割节点和分割集群两种方法。由于调度车辆存在容量限额，因此考虑使用这两种方法[1]。

3 基于遗传-蚁群融合算法的集群间优化调度

3.1 数学模型的建立

实际路况中，连接两节点之间的道路长度和两节点之间的直线距离存在较大差异。为简化计算，用两节点之间的直线距离作为距离指标：

[LθRf=ij∈Rflij]                               （1）

其中，[Lθ]是总距离指标;[Rf]是由融合算法得到的访问节点的顺序;[lij]是站点[Ni]到站点[Nj]的距离。

先在集群层面做出路由决策，然后针对每个节点执行详细的自行车装卸载决策：

[minEk-S0k-Dk]                            （2）

[s.t.Ck<Dk<00<Dk<V-CkCk+1=Ck+Dk，k∈Rf2，Rf3，…，Rfn当k=Rf1时，Ck=0]   （3）

其中，[Ek]为第k个集群节点自行车的目标数量;[S0k]为调度前的自行车数量;[Dk]为对该节点的装卸载操作;[Ck]为访问该节点前调度车内的自行车数量;V是调度车容量。

3.2 遗传-蚁群融合算法求解目标函数

本文提出了一种遗传-蚁群融合算法，将蚁群算法和遗传算法进行优势互补，用于解决集群之间的自行车调度问题，以期达到最小距离成本的目标。该算法以蚁群算法为基础，依据遗传算法得到初始较优解，并考虑调度任务的完成时间，基于综合适应值对路径信息进行初始化，生成初始信息素分布，然后依据蚁群算法进行选择、遍历，并更新节点路径信息素，最终获取精确解[2]。

基本步骤如下。

步骤1：随机生成初始种群，设定种群规模;

步骤2：选择操作;

步骤3：执行遗传算子（交叉、变异）;

步骤4：进行GA终止条件判断，若满足终止条件则转步骤5;否则，转步骤2;

步骤5：从GA得到的解中选择1%个体作为较优解输入ACO;

步骤6：以Ant-cycle模型为基础，对ACO中节点的路径进行信息素初始化;

步骤7：ACO中的参数初始化;

步骤8：应用ACO寻优，构造MRO维修调度问题的可行解，并更新信息素浓度;

步骤9：进行ACO终止条件判断，若满足终止条件，则转步骤10，否则，转步骤8;

步骤10：输出最优解，算法结束。

4 集群内部优化调度

集群内部调度存在范围小、运送量小的问题。解决此问题的方法有蚁群算法、禁忌搜索算法及遗传优化算法[3]。为减小计算复杂度，采用蚁群算法找到每个集群内连接所有站点的最短路径，并按照顺序依次访问每个站点。

5 实例验证与分析

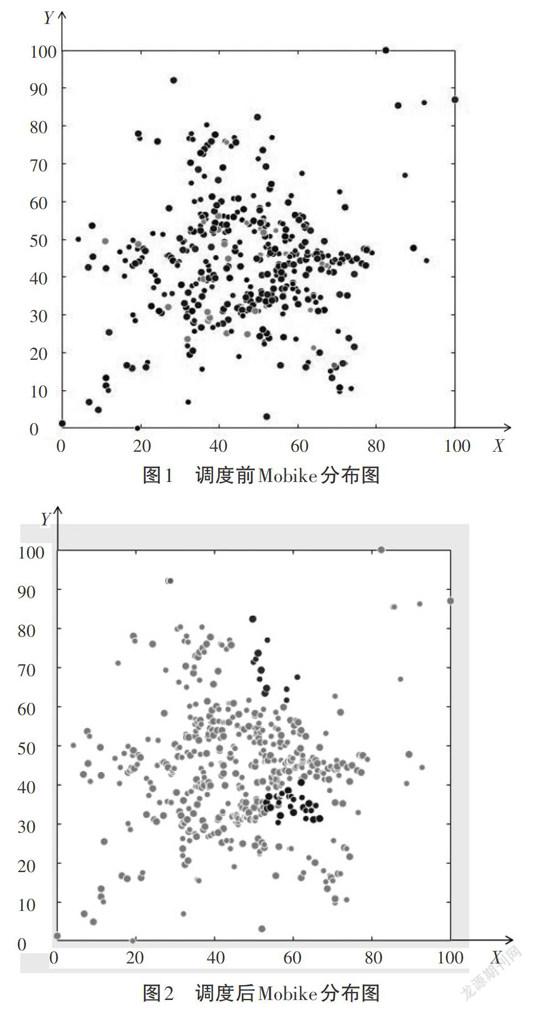
以北京Mobike的494个站点为例，采用遗传-蚁群融合算法，以MATLAB为实现工具，调度前后自行车需求分布如图1和图2所示。

为计算分析方便，将自行车实际的经纬位置转化为横向地理单位为100、纵向地理单位为100的网格，图2中X、Y轴分别为横向与纵向地理坐标轴，点的大小代表站点容量大小。其中，灰色站点代表自行车利用率高的站点;蓝色代表正需求，即需要调来自行车;红色代表负需求，即可以调走自行车;颜色越深，则需求越强烈。负需求无需缓解，因为多余的自行车不会造成任何损失，反而可以为更多人提供服务。调度后，灰色站点数量明显增多，蓝色站点数量急剧减少，可更好地满足出行需求。

<F：＼欢欢文件夹＼201904＼河南科技201901＼河南科技（创新驱动）2019年第01期_103595＼Image＼image15.png>[Y][100

90

80

70

60

50

40

30

20

10

0][0               20             40              60             80             100     X]

图1 调度前Mobike分布图

<F：＼欢欢文件夹＼201904＼河南科技201901＼河南科技（创新驱动）2019年第01期_103595＼Image＼image16.png>[Y][100

90

80

70

60

50

40

30

20

10

0][0               20              40             60              80            100      X]

图2 调度后Mobike分布图

6 结语

本文提出了基于遗传-蚁群融合算法的三步调度法，有效解决了城市内公共自行车系统分布不平衡的问题，节约了调度距離时间成本。

参考文献：

[1]陈文兰，戴树贵.旅行商问题算法研究综述[J].滁州学院学报，2006（3）：1-6.

[2]聂兆伟，熊丹丹，杨海成.基于混合遗传一蚁群算法的MRO服务调度研究[J].计算机应用研究，2018（2）：438-440.

[3]张建国，吴婷，蒋阳升.基于蚁群算法的公共自行车系统调度算法研究[J].西华大学学报，2014（3）：70-76.