单O型密封圈实现双面密封问题的探究

高军 王鹏远

摘 要：密封是液压元件面临的永恒问题。密封结构的选择不但影响产品的密封性能，也关系着产品的体积、重量及经济性等关键指标。通常情况下，一道密封圈只能在一个方向上进行密封，而本文将探讨密封结构中如何实现一个O型密封圈对两个高压面实现密封。具体地，通过建立数学分析模型，结合实际密封需求，参考密封相关标准，给出参考密封形式和密封圈参数，从而为密封结构的选择和结构设计提供参考。

关键词：O型密封圈;双面密封;数学模型

中图分类号：TU991.36 文献标识码：A 文章编号：1003-5168（2019）01-0041-03

Research on Single O-ring Sealing about Double-face Problem

GAO Jun WANG Pengyuan

（Avic Xinxiang Aviation Industry （Group） Co.， Ltd.，Xinxiang Henan 453000）

Abstract： Sealing is an eternal problem faced by hydraulic components. The choice of sealing structure not only affects the sealing performance of products， but also relates to the volume， weight， economy and other key indicators of products. Normally， a sealing ring in one direction only， this article discussed the seal structure of how to implement a type O-ring sealing ring surface of two sealing seal， by establishing a mathematical analysis model， combining with the actual seal requirements， reference seal related standards， reference sealing， and sealing ring parameters were given， provide a reference for the choice of sealing structure and the structure design.

Keywords： O-ring sealing;double-face;mathematical model

低壓液压元件密封结构中，O型密封圈一般实现的是单面密封，即只是一个方向的压紧，使密封圈具备一定的压缩量，进而达到密封油路的需要。有时候根据结构空间的要求，很难有空间实现结构上的双面密封设计，不得不采用一个O型密封圈同时实现两面密封的形式。实际应用时，面临如何选择密封圈尺寸和如何保证结构合理的问题。同时，由于设计不合理，密封量设计不合适和密封槽设计不合适，都将导致密封圈处在不合理的压缩状态，缩短其使用寿命，且在拆装后无法继续使用。因此，只有合理选择结构，才能避免该类问题的发生。

1 密封结构形式

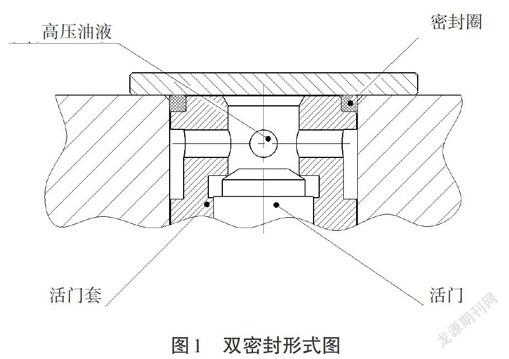
在某项液压泵产品的研制过程中，活门处面需要O型密封圈实现密封两个方向的高压油液与外界的物理隔离。图1描述了这种双面密封的形式，O型密封圈同时完成了两个高压区与外界的物理隔绝[1]。

<F：＼欢欢文件夹＼201904＼河南科技201901＼河南科技（创新驱动）2019年第01期_103595＼Image＼image1_3.png>[活门套][高压油液][活门][密封圈]

图1 双密封形式图

对密封截面进行分析，其截面如图2所示。

图2中，密封圈同时密封了两个面。图2只是理想状态下的密封圈形状，由于受到一定的侧向压力，密封圈实际是会受到一定挤压而发生变形[2]。这种变形又被密封沟槽的形状与大小限制。为了保证密封时密封圈处在可控的变形状态，需要根据密封要求，抽象处理数学模型，并在模型基础上分析密封圈的过盈量、密封沟槽尺寸等参数。

<F：＼欢欢文件夹＼201904＼河南科技201901＼河南科技（创新驱动）2019年第01期_103595＼Image＼image2_3.png>[高压油液][高压油液]

图2 截面分析图

2 数学模型建立分析计算

根据机械设计手册中密封圈密封量选用的设计要求，选择相关参数[3]。建模时，将密封圈的过盈量定义为[Δα]。通常情况下，密封压力的不同会调整所需的过盈量，但通常过盈量都在0.3～0.5mm。同时，理想状态下密封圈压缩变形后总侧面积没有发生变化。根据对密封圈正常状态与密封状态下的侧面积分析，抽象密封时理想的密封状态模型，建立数学关系式，分离出过盈量、密封圈直径和沟槽大小的方程[4]，见图3。

<F：＼欢欢文件夹＼201904＼河南科技201901＼河南科技（创新驱动）2019年第01期_103595＼Image＼image4_1_1.png>[Δx][b][a][Δx][d]

图3 数学模型分析图

假设密封圈压缩后，其截面积正好能填充整个密封沟槽，则建立如下方程：

[πd24=a+Δxb+Δx]                   （1）

其中，[Δx]表示配合间隙。根据需求，一般要求d取最小值时最符合经济性。

[d=4a+Δxb+Δxπ]                        （2）

根据分析，当[a=b]时d取得最小值。假设密封圈过盈量为[Δα]，且密封圈压缩后总截面积不变，则：

[d=a+Δx+Δα ]                            （3）

进一步简化数学模型（一般情况下不考虑[Δx]），则可设[A=a+Δx=b+Δx]，联立以上方程得：

[d=A+Δα=2Aπ]                                （4）

解得：

[A=πΔα2-π]                                      （5）

3 结合实际修正理论数学模型

实际情况中，一般沟槽密封尺寸的单边公差为名义尺寸的a%，密封圈正公差一般为名义尺寸的b%。此时，保证密封圈截面积与沟槽截面积的相应关系就能保证密封性的同时保证密封圈不被损坏，则：

[πd24×1+0.032≤A2×1-0.012]      &nbsp;      （6）

设[K2=1-a21+b2]，即[K=1-a1+b]，又[d=A+Δα]，解得[A=πΔα2K-π]。

为了保证密封性能，密封圈过盈量一般选择0.3、0.4、0.5mm，沟槽单边公差1%、密封圈正公差3%。带入方程，解得A=3.452mm、4.603mm、5.753mm。

密封圈尺寸与沟槽尺寸关系如图4所示。

<F：＼欢欢文件夹＼201904＼河南科技201901＼河南科技（创新驱动）2019年第01期_103595＼Image＼KBL4$（WA@D`G{{E5_5AAXR8.png>[][密封沟槽最小宽度mm][沟槽尺寸][过赢量mm][7

6

5

4

3

2

1

0][0.3][0.4][0.5]

图4 密封圈尺寸与沟槽尺寸曲线图

根据A的方程可知，A关于[Δα]的函数为一次单增函数，解得的A为关于[Δα]的最小值。

根据上述计算，实际需求密封圈与密封沟槽尺寸都较大。对于精密液压元件来说，密封沟槽和密封圈选择都较大，需通过控制沟槽的最小尺寸和密封圈最大尺寸来保证选择较小的密封圈来满足要求，且密封圈公差选择要满足密封过盈量的要求。通过增加沟槽的宽度和减小密封圈的最大截面直径的方式，保证可以选择较小的密封圈。精密液压元件密封圈直径一般选择Φ3.75mm及以下的密封圈，而不考虑实际公差，密封圈的最小直径Φ2.33mm。因此，密封圈一般选择Φ2.8、Φ3.15、Φ3.75mm的密封圈。密封量一般为密封圈直径的8%～15%，相对公差对应的沟槽尺寸应控制在（2.5±0.03）×（2.5±0.03）、（2.82±0.03）×（2.82±0.03）、（3.42±0.03）×（3.42±0.03）。密封圈的公差应控制在（Φ2.8±0.1）mm、（Φ3.15±0.1）mm、（Φ3.75±0.1）mm。

4 结语

本文提供选择双面密封圈时的计算公式和密封圈、密封沟槽的选择方式。在密封圈和密封沟槽较大如大于Φ5.8mm以上时，一般的公差等级即能够满足使用要求;当密封圈在Φ2.8～Φ5.8mm时，应当合理控制沟槽和密封圈公差范围，进而满足密封性能和密封圈不被损坏;当密封圈直径小于Φ2.8mm时，不能同时满足密封能力和密封圈完整程度。此外，根据理论计算，给出了一般小型液压元件使用的密封圈和密封沟槽建议使用公差范围。

综上所述，本文通过建立理想状态下的数学模型，结合标准中对密封结构的相关要求，解决了精密液压元件使用一个密封圈同时密封两个高压面的问题，并提供了标准的密封圈选择和密封结构设计参数，对提高产品的经济性具有积极意义，且能整体上提高产品的结构紧凑性。

参考文献：

[1]成大先.机械设计手册[M].北京：化学工业出版社，2008.

[2]中国航空工业总公司.O型密封圈及密封结构设计要求：HB/Z4—1995[S].1995.

[3]中国航空工業总公司.O形橡胶密封圈 验收规范：HB 7521—1997[S].1997.

[4]同济大学数学系.高等数学（上、下册）[M].北京：高等教育出版社，2007.