RSSR机构的ADAMS参数化建模及优化技术研究

崔素华 张景梅 杨松林 丁朝鹏

摘要：为对空间RSSR四杆机构进行优化设计，以RSSR机构为研究对象，运用解析法对RSSR机构进行了运动学分析，得出RSSR机构的运动解析式，确定曲柄存在条件的表达式;利用ADAMS软件参数化编程技术，将空间四杆机构关键点参数化，构建三维参数化模型;运用ADAMS软件的二次开发技术，开发了空间RSSR四杆机构的参数化建模及分析优化系统，实现了RSSR机构运动类型的判定、快速建模、机构仿真、运动分析及优化，并进行了实例分析。结果表明，对于给定的RSSR机构，系统运动分析优化后，摇杆的角速度、角加速度的最大值和最小值的绝对值明显减小，摇杆摆动速度趋于平稳。研究结果对提高RSSR机构的设计效率、减少设计周期具有参考价值。

关键词：计算机辅助设计;ADAMS;RSSR;參数化建模;优化设计

中图分类号：TH112;TH113.2 文献标志码：A doi： 10.7535/hbgykj.2019yx01001

CUI Suhua， ZHANG Jingmei， YANG Songlin， et al.Research on ADAMS parametric modeling and optimization technique of RSSR mechanism[J].Hebei Journal of Industrial Science and Technology，2019，36（1）：16.Research on ADAMS parametric modeling and optimization

technique of RSSR mechanism

CUI Suhua， ZHANG Jingmei， YANG Songlin， DING Zhaopeng

（School of Mechanical Engineering， Hebei University of Science and Technology， Shijiazhuang， Hebei 050018， China）

Abstract：In order to study the optimal design of spatial RSSR fourbar mechanism， taking RSSR mechanism as the research object， the kinematics analysis is carried out by using analytical method to obtain the kinematics analysis formula of RSSR mechanism， and the expression of crank existence condition is determined; by using parametric programming technology of ADAMS software， the key points of spatial fourbar mechanism are parameterized and the threedimensional parameterized model is constructed; by using the secondary development technology of ADAMS software， the parametric modeling and analysis optimization system of spatial RSSR fourbar mechanism are developed， which realizes the determination of motion type， rapid modeling， mechanism simulation， motion analysis and optimization for the RSSR mechanism. Finally， an example is analyzed. The results show that for a given RSSR mechanism， and after optimization of system kinematic analysis， the absolute values of the maximum and minimum of the angular velocity and acceleration of the rocker are obviously reduce， and the swing speed of the rocker tends to be stable. The research result may provide reference for improving machine design efficiency and shortening design cycle .

Keywords：computeraided design; ADAMS; RSSR; parametric modeling; optimization design

在工业机械中，空间连杆机构比平面杆机构具有更紧凑的结构外形、更复杂的运动形式，可用更少构件实现复杂多样的空间轨迹，工作可靠性更高[13]，应用范围广泛。如剑织机的引纬机构，飞机中的升降舵传动机构、副翼操纵机构等。含有首末2个转动副和中间2个球面副的空间四杆机构一般用RSSR表示。近20年，关于空间RSSR四杆机构的研究方法主要有矢量法、解析法、方向余弦矩阵法、复数法、图解法等[47]。图解法需从三维到二维投影变换，作图复杂，在二维平面内难以完整表达机构的三维几何信息，准确性差[8]。解析法需运用向量或矩阵等数学工具，计算量大，计算机编程复杂[9]。为提高空间RSSR四杆机构的设计效率，运用ADAMS软件及其二次开发技术，开发出空间RSSR机构参数化建模分析优化系统[1015]，实现常用空间四连杆机构的快速参数化建模、仿真分析和优化设计等功能，明显缩短空间RSSR机构的设计研发周期。

1空间RSSR机构参数化建模

1.1RSSR机构曲柄存在的判定

空间RSSR机构模型如图1所示，假设杆AB为曲柄，建立直角坐标系oxyz，点A，B，C，D为铰链点，点A位于xoz平面，点D位于xoy平面，连接BD，过BD做杆CD运动平面的垂直平面BDM，与点C的运动圆弧交于C1，C2，取BC1长度为L′2，BC2长度为L″2（L″2>L′2）。由于BM平行于x轴，则∠BMD为直角，通过BMC1和BMC2求出L′2，L″2的表达式（1）、式（2）。

第1期崔素华，等：RSSR机构的ADAMS参数化建模及优化技术研究河北工业科技第36卷图1空间RSSR机构模型

Fig.1Spatial RSSR mechanism model

L′2=

（（Lz cos α+L1 cos θ sin α）2+（Ly-L1 sin θ）2-

2L1（Lz cos α+L1 cos θ sin α）2+（Ly-L1 sin θ）2+

L23+（Lx+Lz sin α -L1 cos θ cos θ）2）1/2，（1）

L″2=

（（Lz cos α+L1 cos θ sin α）2+（Ly-L1 sin θ）2+

2L1（Lz cos α+L1 cos θ sin α）2+（Ly-L1 sin θ）2+

L23+（Lx+Lz sin α -L1 cos θ cos α）2）1/2，（2）

式中：L1为曲柄AB的长度;L2为连杆的BC的长度;L3为摇杆CD的长度;Lz为A点距原点的距离;Ly为D点y坐标值;Lx为D点x坐标值;α为L1的旋转轴线与z轴正向夹角;θ为杆AB与xoy平面的夹角。

当曲柄AB在任一角度时，连杆BC的长度L2一定介于L′2和L″2之间，当曲柄AB在θ∈（0°，360°）范围之内，只要满足L′2max<L2<L″2min，就满足RSSR机构曲柄成立的条件。

同理，当杆CD为曲柄时，得到式（3）、式（4）。

L′2=

（（Lx cos α+L3 cos θ sin α）2+（Ly+L3 sin θ）2-

2L1（Lx cos α+L3 cos θ sin α）2+（Ly+L3 sin θ）2+

L21+（Lz+Lx sin α -L3 cos θ cos α）2）1/2，（3）

L″2=

（（Lx cos α+L3 cos θ sin α）2+（Ly+L3 sin θ）2+

2L1（Lx cos α+L3 cos θ sin α）2+（Ly+L3 sin θ）2+

L21+（Lz+Lx sin α -L3 cos θ cos α）2）1/2，（4）

以θ∈（0°，360°）为变量，分别求出L′2min，L′2max，L″2min和L″2max。当L1<L3时，满足L′2max<L2<L″2min时，构成空间曲柄摇杆机构，杆AB为曲柄，杆CD为摇杆;当L′2min<L2<L′2max或L″2min<L2<L″2max时，构成空间双摇杆机构;当L2<L′2min或L2>L″2max时不能构成空间RSSR机构。当L1>L3时与L1<L3时分类情况类似，不同之处在于，构成空间曲柄摇杆机构时，杆CD为曲柄，杆AB为摇杆。

1.2RSSR机构参数化模型建立

1.2.1 RSSR机构初始位置的确定

在ADAMS/View中创建的机构模型不能随鼠标拖动改变模型的形态，因此建模前需要对RSSR机构的初始位置确定。

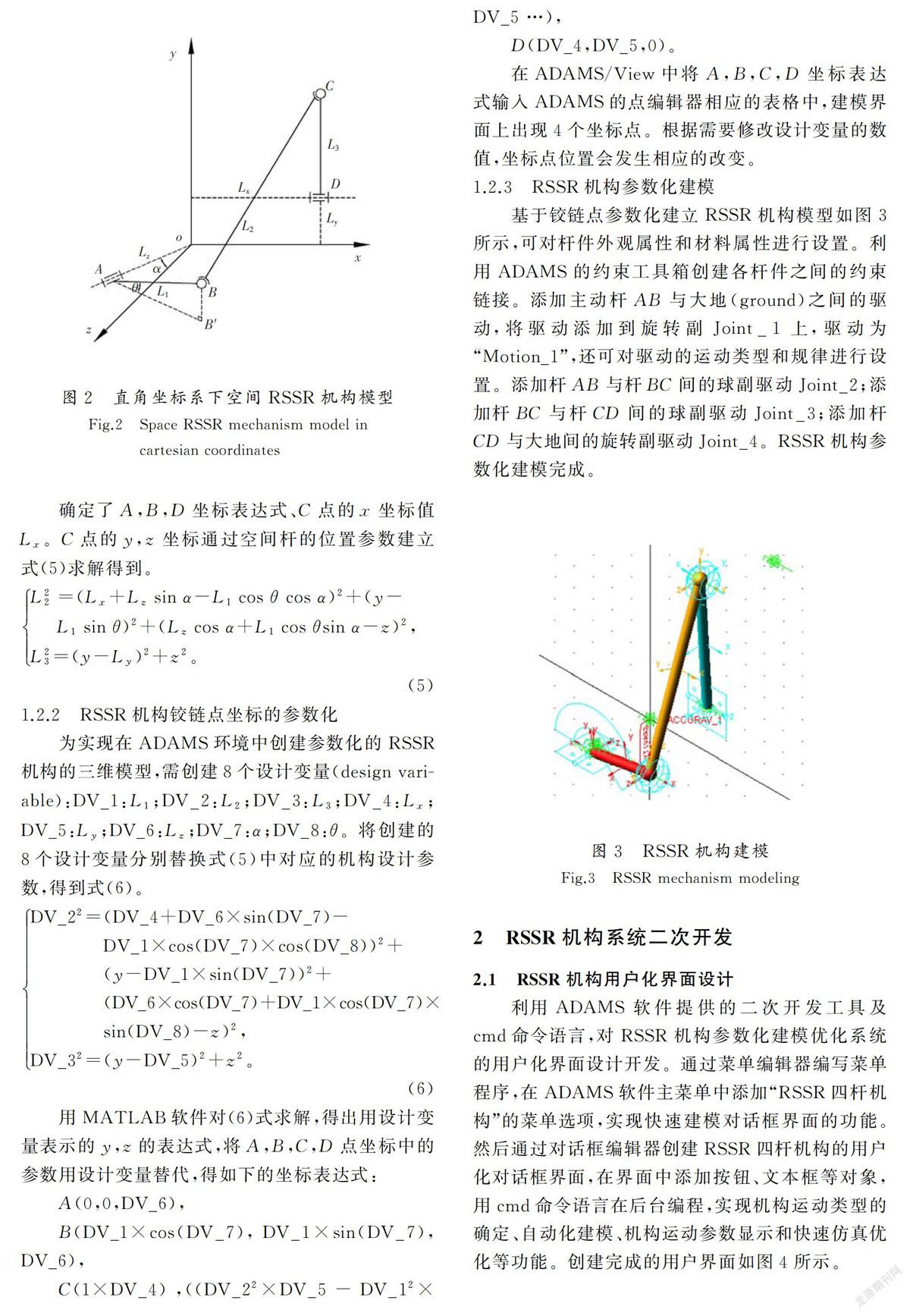
直角坐标系下空间RSSR机构模型图如图2所示，杆AB为曲柄，CD为摇杆时，图中各参数的意义同图1。A，B，C，D关键点的初始坐标分别为A（-Lz sin α，0，Lz cos α），B（-Lz sin α+L1 cos θ cos α，L1 sin θ，Lz cos α+L1 cos θ sin α），C（Lx，y，z），D（Lx，Ly，0）。

确定了A，B，D坐标表达式、C点的x坐标值Lx。C点的y，z坐标通过空间杆的位置参数建立式（5）求解得到。

L22=（Lx+Lz sin α-L1 cos θ cos α）2+（y-L1 sin θ）2+（Lz cos α+L1 cos θsin α-z）2，L23=（y-Ly）2+z2。         （5）

1.2.2RSSR機构铰链点坐标的参数化

为实现在ADAMS环境中创建参数化的RSSR机构的三维模型，需创建8个设计变量（design variable）：DV_1：L1;DV_2：L2;DV_3：L3;DV_4：Lx;DV_5：Ly;DV_6：Lz;DV_7：α;DV_8：θ。将创建的8个设计变量分别替换式（5）中对应的机构设计参数，得到式（6）。

DV_22=（DV_4+DV_6×sin（DV_7）-DV_1×cos（DV_7）×cos（DV_8））2+（y-DV_1×sin（DV_7））2+（DV_6×cos（DV_7）+DV_1×cos（DV_7）×sin（DV_8）-z）2，DV_32=（y-DV_5）2+z2。（6）

用MATLAB软件对（6）式求解，得出用设计变量表示的y，z的表达式，将A，B，C，D点坐标中的参数用设计变量替代，得如下的坐标表达式：

A（0，0，DV_6），

B（DV_1×cos（DV_7）， DV_1×sin（DV_7），DV_6），

C（1×DV_4） ，（（DV_22×DV_5 - DV_12×DV_5 …），

D（DV_4，DV_5，0）。

在ADAMS/View中将A，B，C，D坐标表达式输入ADAMS的点编辑器相应的表格中，建模界面上出现4个坐标点。根据需要修改设计变量的数值，坐标点位置会发生相应的改变。

1.2.3RSSR机构参数化建模

基于铰链点参数化建立RSSR机构模型如图3所示，可对杆件外观属性和材料属性进行设置。利用ADAMS的约束工具箱创建各杆件之间的约束链接。添加主动杆AB与大地（ground）之间的驱动，将驱动添加到旋转副Joint_1上，驱动为“Motion_1”，还可对驱动的运动类型和规律进行设置。添加杆AB与杆BC间的球副驱动Joint_2;添加杆BC与杆CD间的球副驱动Joint_3;添加杆CD与大地间的旋转副驱动Joint_4。RSSR机构参数化建模完成。

2RSSR机构系统二次开发

2.1RSSR机构用户化界面设计

利用ADAMS软件提供的二次开发工具及cmd命令语言，对RSSR机构参数化建模优化系统的用户化界面设计开发。通过菜单编辑器编写菜单程序，在ADAMS软件主菜单中添加“RSSR四杆机构”的菜单选项，实现快速建模对话框界面的功能。然后通过对话框编辑器创建RSSR四杆机构的用户化对话框界面，在界面中添加按钮、文本框等对象，用cmd命令语言在后台编程，实现机构运动类型的确定、自动化建模、机构运动参数显示和快速仿真优化等功能。创建完成的用户界面如图4所示。

2.2RSSR机构自动分析和设计优化

建模完成后对机构进行运动仿真。用cmd命令语言编程调用ADAMS的仿真分析和设计优化等模块，对相应按钮添加后台程序。仿真分析模块可实现机构仿真的时间和步数的设定，机构运动仿真有“开始”、“暂停”、“重置”等功能的控制。

设计优化模块实现了仿真结果曲线的记录和快速查看，例如测量RSSR机构摇杆的角位移、角速度、角加速度等结果曲线，以及对ADAMS后处理模块和优化设计模块的调用。

3实例分析及验证

3.1实例建模与仿真

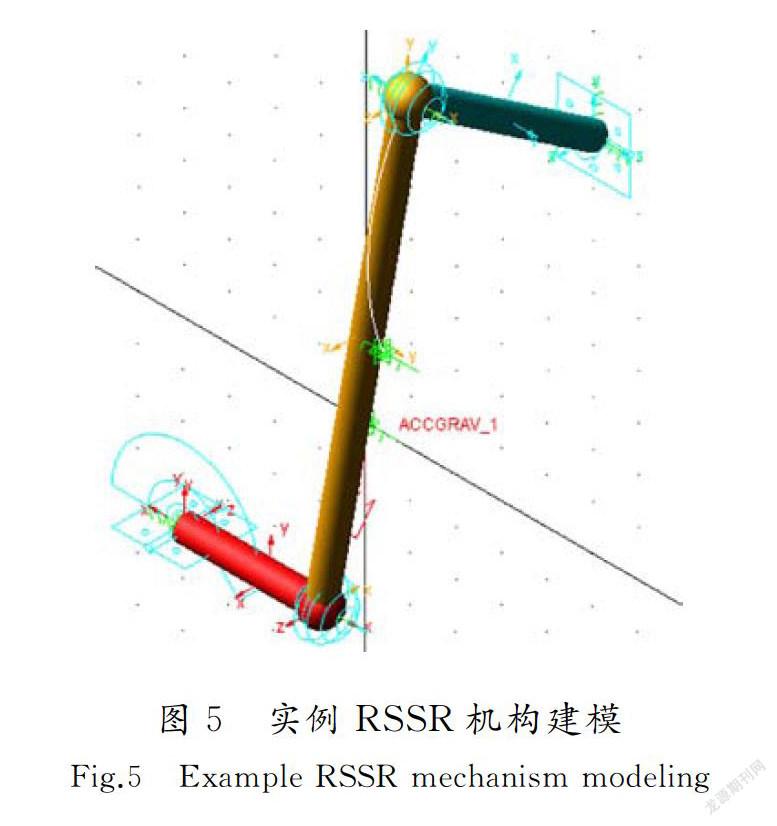
给定一个RSSR机构的初始参数，L1=30 mm，L2=110 mm，L3=50 mm，Lx=50 mm，Ly=80 mm，Lz=40 mm，α=0°，曲柄转速ω=360°/s，根据实际工况要求以机构的摇杆运动平稳为优化目标，对机构参数进行优化。

在ADAMS环境中打开系统界面。首先设置建模环境：单位MMKS、重力y方向、图标和栅格默认。然后进行参数化建模：在机构参数模块中输入L1=30，L2=110，L3=50，Lx=50，Ly=80，Lz=40、初始角和轴夹角均为0、曲柄转速为360°/s。单击“验证”按钮，系统自动得到杆长数据R1=35.236，R2=92.734，R3=122.067，R4=175994，满足条件，判定机构运动类型为空间曲柄摇杆机构，杆AB为曲柄，摇杆摆角93.376°，曲柄极位夹角为18°，行程速比系数为1.22。创建机构三维模型、添加运动副和驱动，创建的实体尺寸以连杆BC长度L2为基础，杆半径为L2的1/40，球的半径为L2的1/30。创建完成的空间RSSR机构的实体如图5所示。设置机构仿真的时间为12 s、步数为360步，并进行运动仿真。

3.2实例优化设计

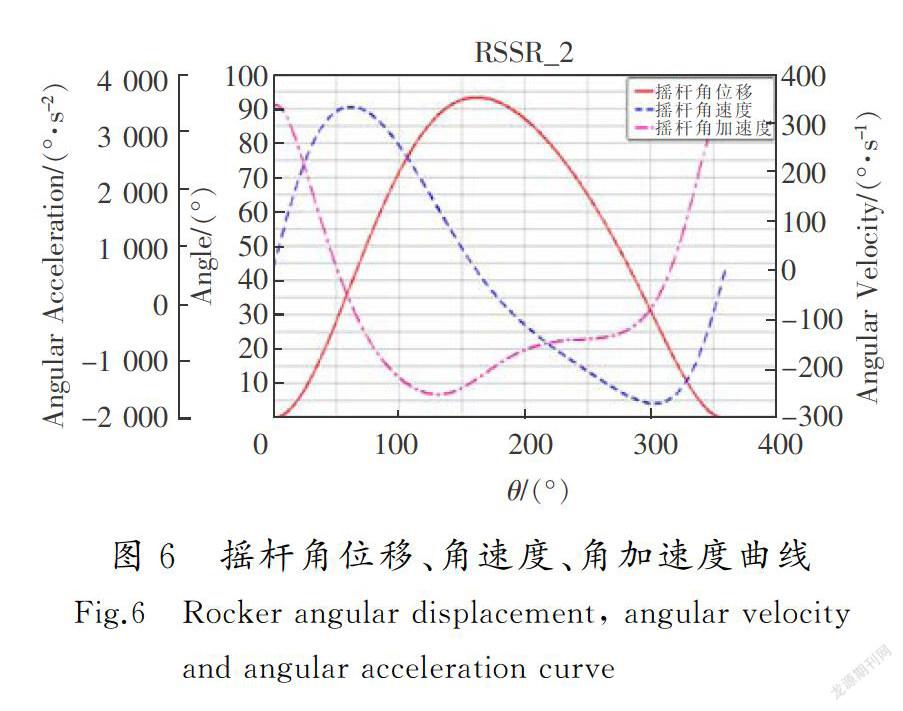
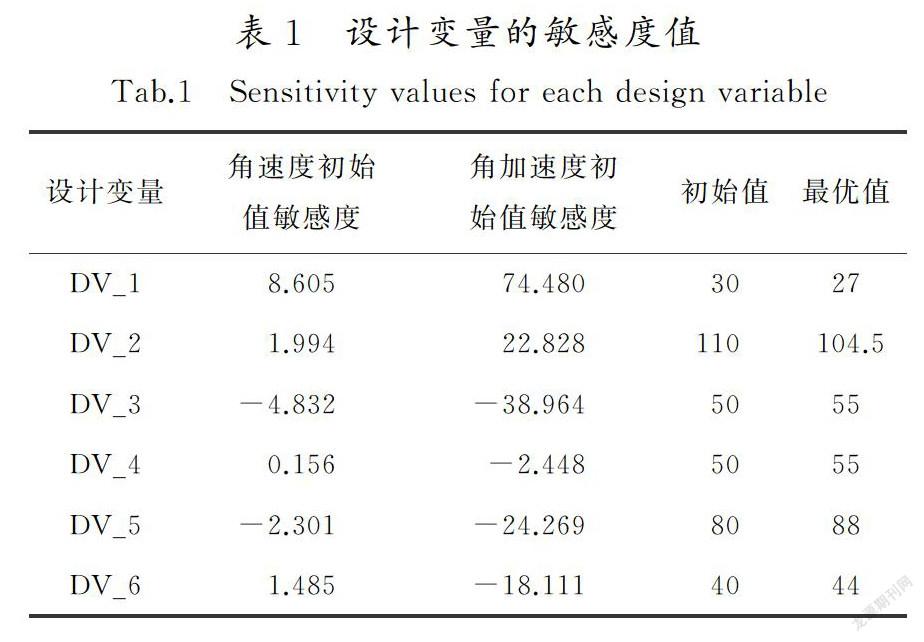
测出摇杆CD的角位移、角速度和角加速度曲线，如图6所示。对机构参数进行优化，使摇杆的摆动最平稳。首先确定优化目标函数，将摇杆角速度和角加速度的标准偏差最小为优化目标;研究设计变量的变化对摇杆速度波动的影响，得出目标函数对设计变量的敏感度，并筛选出敏感度较大的设计变量，如表1所示。

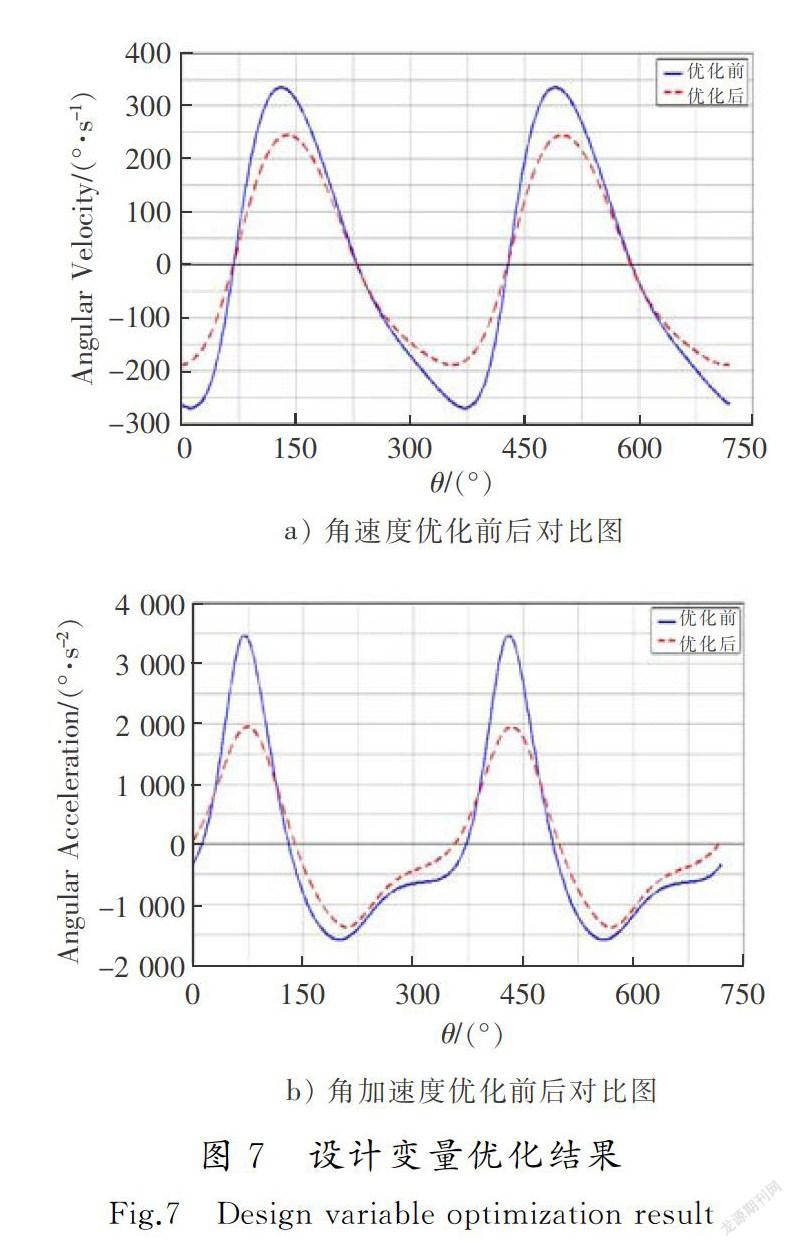
始值敏感度初始值最优值DV_18.60574.4803027DV_21.99422.828110104.5DV_3-4.832-38.9645055DV_40.156-2.4485055DV_5-2.301-24.2698088DV_61.485-18.1114044通过表1可知：DV_4的初始值敏感度远小于其他变量敏感度，可不考虑。对其他设计变量进行设计优化。优化前后的角速度和角加速度对比曲線如图7 a）和图7 b）所示，实线为优化前的曲线，虚线为优化后的曲线。角速度最大值从334.905 °/s变为245152 °/s，减小了26.8%，最小值从-269.698 °/s变为-187.793 °/s，减小了30.4%;角加速度的最大值从3 469.381 °/s2变为1 949.399 °/s2，减小了43.8%，最小值从-1 579.476 °/s2变为-1 365.653 °/s2，减小了13.5%。优化后的角速度、角加速度的最大值和最小值的绝对值都明显减小，以优化后的数值重新建模仿真，摇杆摆动速度明显缓和，优化效果良好。

4结语

对RSSR机构的ADAMS参数化建模及优化技术进行了研究。实例分析表明，系统能够快速、准确判断空间RSSR四杆机构的运动类型，创建机构三维模型，实时显示机构的运动参数，方便、快捷地进行机构仿真和优化设计，提高了三维空间四杆机械的设计效率。将三维参数化建模技术应用于空间多杆机构，无需用户列公式，只需给出各个杆件的长度参数，系统即可将多种不同分析结果迅速输出。不足之处是所开发的系统只是对RSSR四杆机构进行了分析，同时其运动参数的判断时间较长。未来需对其他空间四杆甚至五杆、六杆机构等进行研究，从而使系统得到进一步完善。

参考文献/References：

[1]张春林， 余跃庆. 高等机构学[M]. 2版.北京：北京理工大学出版社，2006.

[2]谢可兵， 矛及愚. 空间连杆机构的研究和应用[J]. 新技术新工艺， 2003（7）：16-18.

XIE Kebing， MAO Jiyu. Research and application of spatial linkage mechanism[J]. New Technology & New Process， 2003（7）：16-18.

[3]SU H， MCCARTHY J M. Classification of design for RRSS linkages[J]. Mechanism and Machine Theory， 2002，37： 1413-1433.

[4]曹茹. 基于三维参数化的空间RSSR机构设计图解法[J].中国农机化学报， 2016，37（10）： 266-268.

CAO Ru.Graphic method of spatial RSSR mechanism design based on 3D parameter[J].Journal of Chinese Agricultural Mechanization，2016，37（10）：266-268.

[5]左传，陈晓航. 基于解析法的RSSR机构运动精度及可靠性分析[J]. 机械研究与应用， 2016， 29（4）： 61-63.

ZUO Chuan， CHENG Xiaohang. Analysis of motion precision and reliability of RSSR mechanism based on analytic method [J]. Mechanical Research and Application， 2016， 29（4）： 61-63.

[6]周啸，宋梅利，王晓鸣. RSSR空间机构的运动分析和优化设计[J]. 机床与液压，2015，43（9）： 1-4.

ZHOU Xiao， SONG Meili， WANG Xiaoming.Motion analysis and optimization design of RSSR space mechanism[J]. Machine Tool & Hydraulic， 2015，43（9）： 1-4.

[7]夏新念. 計算机辅助RSSR型空间曲柄摇杆机构设计[J]. 武汉化工学院学报，2003，25（2）： 78-80.

XIA Xinnian. Design of computer aided RSSR space crank and rocker mechanism [J]. J Wuhan Inst Chem Tech， 2003，25（3）： 78-80.

[8]周勇， 孙海刚. 某型空间RSSR机构的图解分析与设计[J]. 北京理工大学学报， 2011，31（4）： 394-397.

ZHOU Yong， SUN Haigang. Graphical analysis and design of a space RSSR mechanism[J]. Journal of Beijing Institute of Technology， 2011，31（4）： 394-397.

[9]苗鸿宾，乔峰丽. 空间RSSR机构运动分析的研究 [J].机械设计与制造，2008（2）： 7-9.

MIAO Hongbin， QIAO Fengli. Research on motion analysis of spatial RSSR mechanism [J]. Machinery Design & Manufacture， 2008（2）： 7-9.

[10]李大磊，丁天涛.机构运动解析与仿真分析[M]. 北京：化学工业出版社，2014.

[11]SUN Haigang， ZHOU Yong. Kinetic analysis of spatial RSSR mechanism by analytical method [J]. Advanced Materials Research， 2011，215： 320-326.

[12]TANK E，PARLAKTAS V. A new type of compliant spatial four-bar（RSSR）mechanism [J]. Mechanism and Machine Theory， 2011， 46（5）： 593-606.

[13]陈峰华. ADAMS2012虚拟样机技术从入口到精通[M]. 北京：清华大学出版社， 2013.

[14]李增刚. ADAMS入门详解与实例[M]. 北京： 国防工业出版社， 2014.

[15]李军. ADAMS实例教程[M]. 北京： 北京理工大学出版社， 2002.