基于自举抽样的公路养护项目概念阶段成本区间估计分析

秦玲

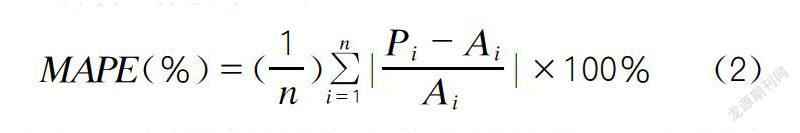
摘要：针对点估計在项目概念阶段成本预测中的不足，文章提出一种基于自举抽样的公路养护项目概念阶段成本区间估计方法，以估计值的概率范围来表示成本的不确定性。分析表明：相较于点估计，区间估计在成本预测中所显现的确定性和预见性更少，也更符合项目概念阶段成本特征。

关键词：成本预测;自举抽样;区间估计;公路养护项目

中图分类号：U418 文献标识码：A DOI：10.13282/j.cnki.wccst.2019.10.054

文章编号：1673-4874（2019）10-0195-04

0引言

大多数公路养护机构都将项目成本编制视为一个点估计。但点估计的问题在于：它在成本预测中传达了一种错误的信心，可能会导致基于成本估计的资金决策出现预测偏差。具体而言：（1）当成本表示为点估计时，对于那些不知道点估计缺陷的人来说它似乎是准确的，从而造成应用点估计可能会产生一种成本可控与可预见的假象;（2）那些在项目概念阶段使用点估计的人，可能并未意识到最终的实际成本会经历的极端情况或范围波动;（3）点估计会使得管理者过于锚定概念阶段成本的估计结果而存在锚定误差的可能。点估计以特定的假设和相应的单点数值来验证预测结果，对于充满不确定性的项目概念阶段成本来说显然极不合理。因此，本文探索了一种能充分考虑项目不确定性的成本编制新方法。

1文献综述

Koplon在量化风险时认识到概率曲线的优势，并指出点估计不足以表述出成本的不确定性;而区间估计利用广泛的经验来定义一个分布概率范围，相较于点估计在成本预测中所显现的确定性和预见性更少，也更符合项目概念阶段的成本特征。自那时起，区间估计的优势就被许多学者所探索。美联邦公路管理局（FHWA）在其《成本估算指南》中允许公路机构将概念成本估计表述为具有指定置信水平的区间范围。Molenoor为华盛顿州运输部（WSDOT）创建了一种专门针对项目金额超过1亿美元的公路成本区间估计方法，并于最近成功实现此方法。据其描述，区间估计方法更好地传达了项目概念阶段成本的不确定性，通过有效透明的沟通，可以更好地管理公共资金及增强公众信心。尽管该方法有效，但该方法的开发费用高达300万美元，且须长期聘用一位风险专家。因此该方法并不适用于公路养护工程的成本估计。而Sonmez使用自举抽样同多元回归分析（MRA）与人工神经网络（ANN）相结合，成功计算了单个建筑项目的随机区间估计成本值。但是该方法的准确性受限于有限的数据集，若能进一步扩大数据集，模型的鲁棒性及预测性能都能得到有效提升。考虑到ANN预测性能要明显优于MAR，因此本文拟用自举抽样结合ANN，通过显著增加数据集规模，对公路养护工程概念阶段成本进行区间估计。

2 点估计与区间估计建模

为实现研究目的，本文拟分为三个步骤：

（1）建立基于ANN的点估计预测模型，并通过计算平均百分比差（MAPE）来验证模型预测值同实际值的差异性;

（2）使用步骤1中的ANN模型结合自举抽样开发出区间估计模型，得到测试项目的成本预测值及累积分布函数（CDF），并将CDF同实际值进行比较;

（3）比较点估计与随机区间估计的差异性。

2.1点估计模型

经大量问卷调查及结合自身经验，明确了12个与公路养护项目最相关的最佳成本特征指标。此次问卷共发放312份，发放对象为公路养护领域具有多年丰富经验的专业人员。问卷回收份数为202，回收率64.7%，有效份数为192，回收有效率为95.1%，因此本次问卷调查数据本文予以采信。本文为分类输入还创建了高中低复杂性评分表，如地质情况、路权获取困难性等。如表1所述。

表1中地质评定情况为平原=H、丘陵=M、山地=L，面层材料为沥青量化为2，为混凝土则量化为1，路权获取难度依赖专家打分法。使用MATLAB神经网络模块创建一个基础ANN，ANN预测模型构建主要分为三个步骤：初始神经网络的搭建、模型的学习与训练、模型预测。限于篇幅，ANN计算步骤不再赘述，详参文献。

2.2 区间估计

ANN是数据驱动的估计技术，模型输出随所选择的引导样本变化而变化。因此，若能有系统地控制引导样本集来获得相应变化的成本估计值，便可得到成本的区间估计。基于此思路，本文通过组合不同的引导样本集，使用多次迭代的方式来获得成本的估计区间，成本估计值的概率分布可用离散方法或将离散结果转换为连续概率函数。

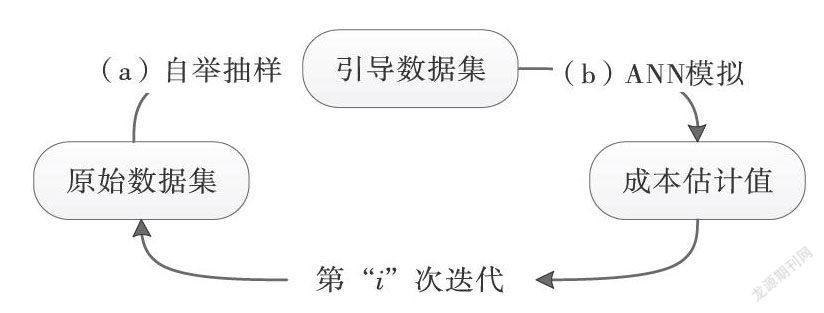
在不使用自举抽样的情况下，产生随机概率的技术的确存在。例如蒙特卡罗模拟通过软件来产生随机概率也可用于模拟结果，但自举抽样具有不依赖原始分布的假设和计算优势。自举抽样提供了一个简单的随机重采样数据集的过程。如图1中，引导数据集通过随机抽取原始数据集的方式产生，引导数据集的取样方式有两种：（1）不放回抽样（WQR）;（2）放回抽样（VR）。WOR抽样是指从从原始数据集中提取指定百分比的项目。在这个过程中，n被定义为引导样本数，N为原始数据集中样本数，并规定n

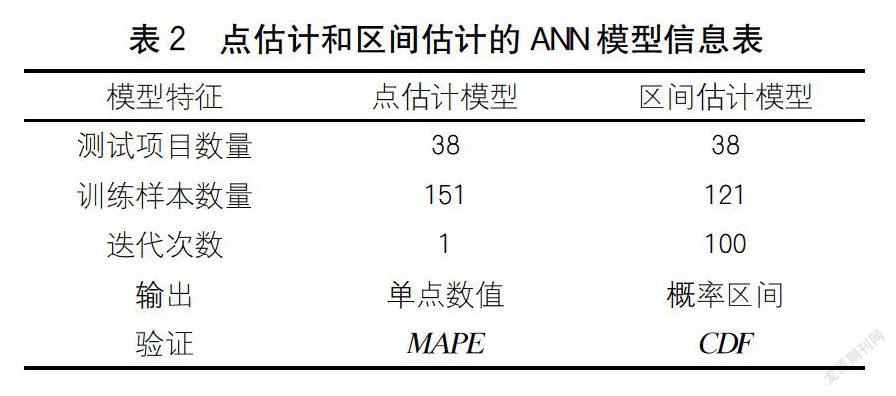
为训练随机区间估计的神经网络预测模型，本文采用引导抽样的方式从151个样本中随机抽取了80%（121个）的项目作为模型的引导样本，然后使用这些引导样本完成神经网络的训练，并以余下38个项目来测试模型的训练结果。考虑计算量将迭代次数设置为100次。由于用于训练ANN模型的121个项目在每次迭代中都是不同的组合，这为38个测试项目分别产生了100个不同的预测值。为建立成本估计值的经验分布，将它们从小到大依次排列，并通过公式（1）来确定每个项目成本估计的概率分布F（i），并利用各自项目成本依次绘制出100个样本水平的累积分布函数（CDF）。

F（i）=i/n （1）

式中：i=1，2，3，…，n，n=100，概率F（i）表示预测值等于低于第i个值的概率。由于此时输出是一个区间，因此无法适用MAPE来评估区间估计的预测性能。相反，为验证随机估计，可将实际成本与CDF进行比较，看其是否包含在概率区间的最大和最小值的范围内。

2.3 区間估计与点估计差异性比较

为比较区间估计与点估计两者的输出差异，在同一个项目中用两种方法进行测试。两种方法应用的具体信息如表2所示。

对于点估计，使用189个项目中的80%（151个引导项目）对ANN模型进行训练，并以余下的38个项目来测试经训练后的ANN模型的预测性能。使用平均百分比差（MAPE）来表示这38个测试项目的点估计误差。MAPE是成本估计模型最常见的验证方法之一，计算式见式（2）：

式中，n为测试数据集中的数据数量，P为测试项目集中第i个项目的预测成本估算，A是测试项目集中第i个项目的实际成本。然而，比较点估计模型的MAPE与区间估计模型的CDF的优劣性是困难的。一个是单点估计值，另一个却是具有相关概率的估计范围。因此，本文将从项目的不确定性角度进行定性分析来评估点估计与区间估计的差异性。

3案例分析及结果

3.1结果一：点估计模型

限于预算及其它原因，本文仅搜集了S地区2010-2016年间所完成的189个公路养护项目成本数据，主要工作为灌缝补强、罩面、局部修补和重铺。189个项目金额从5万元到400万元不等，其中148个是农村项目，41个为市政项目。将这189个项目数据集分为两组：训练组和测试组。鉴于以往研究大多使用20%-30%的项目用于测试模型，因此本文选用了20%（38个）的项目数据以测试模型。项目实际成本应按年通货膨胀系数（3%）折算到基准年（2016），以反映不断上涨的建设成本。

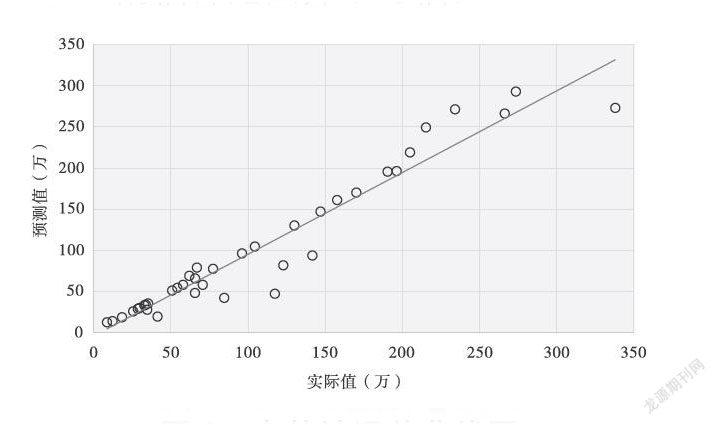
在MATLAB软件的ANN模块中选择3层单隐层网络，激活函数采用S型函数，初始权值为（-0.05，0.05），神经元个数依照“2×输入变量数+1”确定为25个，训练次数设置为1000次，目标误差设置为0.01。ANN模型在测试时表现良好，预测误差较小，38个项目的MAPE为23%，在概念阶段该误差完全符合使用要求。图2显示了38个测试项目估计值与实际值间的关系，图中斜率为1的直线表示估计值与实际值相等。由图2可知，基于ANN的点估计值精度十分不错，估算者似乎可以认为：如果项目使用点估计，那么实际成本值应在预测值的23%以内。但这并非正确，MAPE是根据预测值与实际值的平均误差来计算的，由于没有提供特定的置信水平，因此基于MAPE的估计范围并不可信。

3.2 结果二：区间估计模型

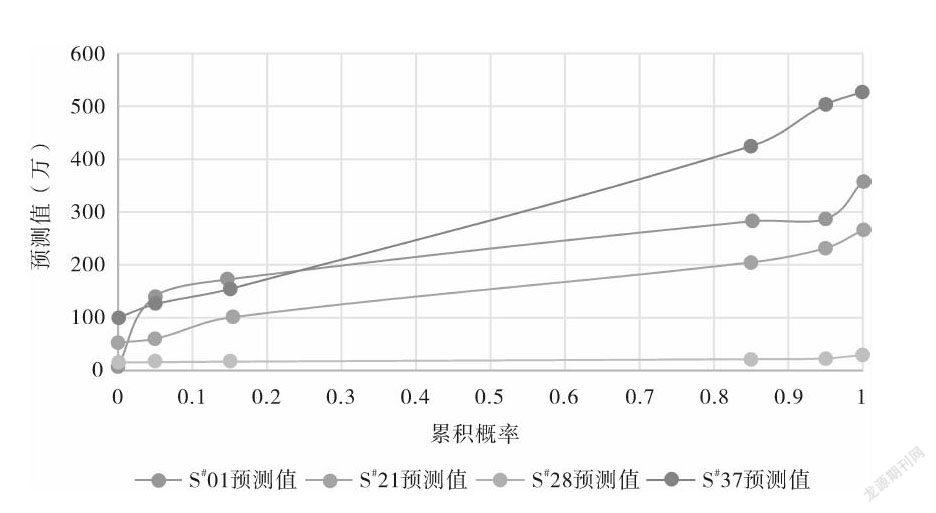
对项目S#01-S#38进行区间估计，限于篇幅，本文仅展示一部分预测结果，如表3所示。最大值和最小值是在100次迭代过程中所产生的两个极值，而5%、15%、85%、95%均表示为成本等于低于该预测值的概率。

本文最大的预测概率范围为90%，即5%-95%，相应的15%-85%表示70%的概率范围，概率范围越窄则表示成本的不确定性越小，即精度越高。据预测结果，38个测试项目有35个位于预测最小值与最大值范围内，有27个位于5%-95%的概率范围内，有18个位于15%-85%的概率范围内。由此可知，随着置信区间的不断缩小更多的项目超出了置信区间，这与实际相符。

图3显示了表3中的4个项目的区间估计结果。项目S*28是一个路面罩面工程，其成本估计的范围极窄，这表明该项目在概念阶段比其它项目更为明确。项目S*01和S# 21分别是长度为7.5km和5.1km的路面重铺工程，由于相似的特点两个项目具有大致平行的概率区间，但由于项目里程影响项目S*21的实际成本与估计值都相对较高。项目S*37显示出的确定性最小，即其估计的最小值与最大值的范围最广。尽管这三个项目的实际成本极为接近，但项目S*37的估计范围却比其它两个项目要大得多。这是因为项目S*37为一个桥梁维护项目，其成本的复杂性和不确定性都较高，在编制项目S*37的概念阶段成本考虑了大量意外因素而实际上却并未发生，从而导致了极宽的估计范围。

对于所有的项目来说，预测的成本值并非是恒定的，其估计值的分布范围取决于该项目信息的不确定性，而并不依赖于实际成本。例如，与项目S*01和S*21相比，项目S*37的实际成本更低但其成本估计值的分布范围却更广。

4 结语

本文研究了如何在公路养护方面利用现有数据进行成本区间估计，及如何正确表达项目概念阶段成本的不确定性。通过在同一组数据中借助ANN程序同时开发点估计与区间估计技术进行差异性分析。研究表明：点估计可以很好地预测项目成本，但此方法可能不太准确，也未显示出成本估计过程中的不确定性;而利用区间估计所产生的随机分布范围，可以很直观地帮助管理者比较各种项目的概念阶段成本。

由于点估计是单值输出并未显示出其置信水平，在项目的后期阶段当工程量明确时，公路项目可以更加准确地以这种形式来表示成本。而在项目信息不明确的概念阶段，成本更应以描述置信水平的方式来表达。但要改变企业从点估计转换到区间估计的成本编制习惯需要巨大的努力。在项目投资回报存在重大不确定性的情况下，使用区间估计的投资决策更具挑战性，它需要一种能够容忍甚至接受这种模糊性的企业文化和魄力。