基于椭球模型下的高校课堂教学可靠性评估

温世峰 王亮亮 张峰

摘  要：文章针对高校“课堂教学失效”这一问题提出了基于椭球模型的故障树分析方法，实现了对高校课堂教学的可靠性的量化评估，对改进教学有指导意义。首先建立以高校“课堂教学失效”为顶事件的故障树模型;然后基于课堂教学数据信息的不充分性和动态特性，采用椭球模型来描述底事件，最后基于蒙特卡洛法理论在椭球模型下计算了顶事件的发生概率，从而实现对高校课程的可靠性评估。

关键词：课堂教学;可靠性评估;故障树;椭球模型;蒙特卡洛

中图分类号：G642 文献标志码：A 文章编号：2096-000X（2019）11-0085-03

Abstract： This paper proposes a fault tree analysis method based on ellipsoid model for the problem of "invalidation of classroom teaching" in colleges and universities， which realizes the quantitative evaluation of the reliability of classroom teaching in colleges and universities， and has guiding significance for improving teaching. Firstly， the fault tree model based on the "invalidation of classroom teaching" in colleges and universities is established. Then， based on the inadequacy and dynamic characteristics of the classroom teaching data information， the ellipsoid model is used to describe the bottom event. Finally， the probability of the top event is calculated under the ellipsoid model based on Monte Carlo method theory， so as to realize the reliability evaluation of college courses.

Keywords： classroom teaching; reliability assessment; fault tree; ellipsoidal model; Monte Carlo

一、概述

课堂教学是关于教学目标、教学内容、教学手段及方法、考核评价等与课堂教学相关的诸要素之间的组合方式和运作流程的标准形式[1]。一些高校采用检查表式多项指标综合评价法对教师的教学效果进行分析和评价，该方法简单易行，可以达到诊断、评价教师教学效果的目的[2]。

目前，已有教育者从培养学生学习兴趣及自主学习能力等方面对课堂的教学效果进行了研究，并取得了一定的成绩，但这些研究多数属于定性的分析，在定量研究方面研究较少[3，4]。

教学系统是由各种复杂的硬件、软件、环境和人等因素组成，简单几项指标很难全部反映系统的运行效果，且不易理清教学系统故障所在以及各因素对教学系统的影响[5，6]。

教学本身是个复杂的系统工程，可采用系统工程的方法对它进行管理和评价。故障树分析（FTA）技术是美国贝尔电话实验室于1962年提出的，它采用逻辑的方法进行分析，特点直观明了、逻辑性强，该技术具有系统性、准确性和预测性[7]。本文以“课堂教学失效”为顶事件，研究课堂教学过程中的薄弱环节，建立其故障树分析模型。然而，在傳统故障树分析中，底事件的发生概率处理为精确值[2]。但对于以“课堂教学失效”为顶事件的故障树分析中，由于缺乏统计数据或受多种因素的影响，难以确定底事件的精确概率。

相对而言，区间模型仅需要不确定事件集合的界限，不需要确定其内部分布情况，对数据的依赖性明显低于概率模型而得到应用[8]。由于在实际中所有底事件的发生概率同时取端点值的概率极低，而且这种可能性随着底事件数目的增多而变得更加微乎其微，高校“课堂教学失效”故障树的底事件众多[2]，使得区间模型下故障树顶事件的失效概率范围过宽，难以具有参考价值，无法满足实际要求。

超椭球模型是对区间模型的优化。在区间模型中，底事件发生概率的所有可能取值都被包含在超椭球域中。相对于区间模型，超椭球模型排除了底事件发生概率的一部分取值范围，椭球域的大小反映了不确定事件的波动程度，一定程度上解决了区间模型结果值范围过宽的问题[9]。

本文在上述研究的基础上，从学生角度选择故障树方法对影响课堂教学效果的因素进行定性筛选，采用“故障树分析法”对高校课堂教学的可靠性进行评估，采用双层蒙特卡洛法对求解模型顶事件发生概率，从而实现对课堂教学可靠性的定量评估。

二、故障树理论基础

故障树分析从一个可能的故障开始，自上而下、一层层的寻找顶事件的直接原因和间接原因事件，直到基本原因事件，并用逻辑图把这些事件之间的逻辑关系表达出来。故障树由事件和逻辑门两大元素构成，故障树中的顶事件、中间事件和底事件的发生与否以“事件”来表示，系统及各部件之间的功能逻辑关系以“逻辑门”来表示[7]。

四、“课堂教学失效”故障树的建立

本文基于文献[2]，建立以“课堂教学失效”为顶事件的故障树，然后对此顶事件基于学生视角逐层展开并分析，找出影响顶事件的原因，从而建立故障树。具体分析如下：造成课堂教学失效的条件主要包括教师、学生和环境，因此将这三者作为故障树的中间事件;然后分别从教师、学生和环境三个方面确定更底层的事件，即影响顶上事件的因素，将其作为故障树的基本事件。主要包括教师的教学方法、教师魅力与授课速度;学生的学习态度、学习动机与学习方法;以及开设习题课、实验课、教学内容与课堂管理10个事件。

运用故障树的符号将确定的顶事件、中间事件和底事件表示出来，并用逻辑门描述各事件之间的逻辑关系。考虑到影响顶事件课堂教学效果的是由中间事件共同确定的，且缺少任一个都不能造成顶事件的发生，且基本事件之间相辅相成共同影响中间事件，因此本文选择与门结构连接顶上事件、中间事件和基本事件。由于本文底事件的选择是将基本事件简化为学生方便回答的互斥问题，因此选择或门结构连接底事件。进而得到“课堂教学失效”故障树如图1所示[2]。

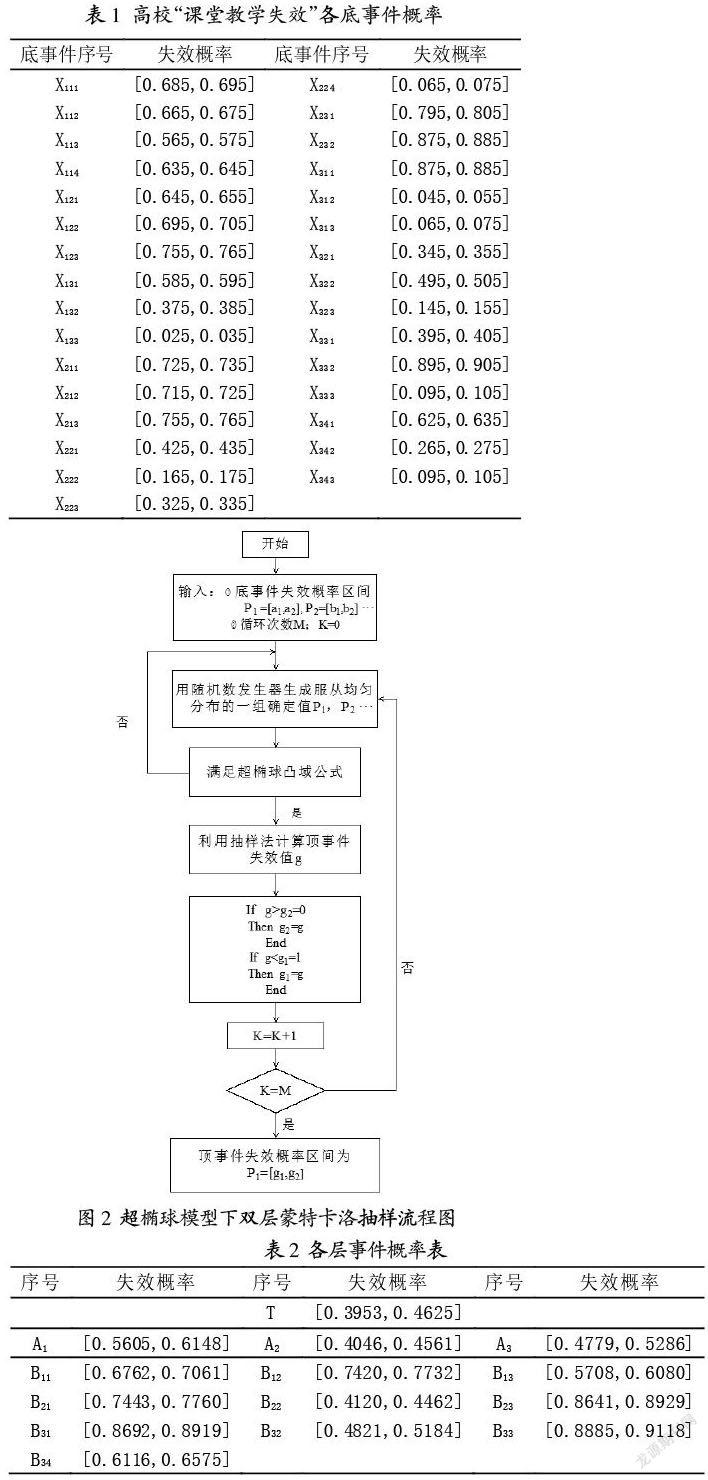
根据所建立的故障树模型，通过收集的相关信息[2]，基于椭球模型理论，再综合不同专家的知识[9]，确定各底事件发生的概率区间，具体见表1所示。

五、椭球模型下“课堂教学失效”的概率分析

蒙特卡洛法是通过对有关随机变量的统计抽样试验或随机模拟，从而估计和描述函数的统计量，进而求解工程技术问题近似解的一种数值计算方法。该方法以统计抽样为基础，以计算机为计算手段，以概率论的大数定理和伯努利定理为理论基础[10]。

本文采用双层蒙特卡洛抽样模拟计算的方法来求解顶事件失效概率。超椭球模型与区间模型主要在于外层抽样的不同，对于区间模型，各底事件失效概率区间内的每一次抽样都视为有效抽样，而对于超椭球模型，在每次对各底事件失效概率区间进行抽样后，都要代入超椭球凸域公式进行判定，若满足则视为有效样本点，若不满足则舍弃并重新进行下一次抽样。

超椭球模型下系统失效概率估算流程图如图2所示[9]。

根据图2中失效概率估算流程图对高校“课堂教学失效”进行定量分析。根据课堂教学效果的故障树结构，在底事件的概率确定以后，依据超椭球模型下系统故障树求解得到故障树中各逻辑门上层事件发生的概率，即对课堂教学有效性的影响程度，见表2。

基于蒙特卡洛法（MCM）收敛准则，设定外层抽样次数为1000，内层抽样次数为10000，经过双重蒙特卡洛法（MCM）抽样计算下的顶事件“教学失效”的概率区间值为[0.3953，0.4625]。

六、结束语

本文在故障树分析方法的基础上引入椭球域来描述导致“课堂教学失效”的底事件发生概率，相比一般方法，既体现了底事件概率的不确定性，同时也排除了极端小概率事件对结果的影响。通过蒙特卡洛法模拟求解故障树得到了教学失效的概率区间，实现了对课堂教学效果概率区间的量化评估。相对于传统教学评估方法，本文提出的评估模型方法便于全面掌握并分析教学系统异常的原因和故障诊断，且具备很大的扩展空间，能更加全面合理地评价课堂教学系统的可靠性，同时后期新的故障事件可加入该基础性的评估模型中，从而在实行过程中采取相应措施改善教学情况。

参考文献：

[1]林静.高校新型课堂教学模式的选择及实现方法[J].中国大学教学，2011，9：74-77.

[2]成琨，任永泰，徐文仲.提高课堂教学效果的故障树模拟分析——基于学生视角[J].河北农业大学学报（农林教育版），2015，17（2）：70-73.

[3]程庆庆.探索高等教育专业课教学效果的途径[J].教育教学论坛，2017，38：152-153.

[4]杨敬华，肖黎.高教低效课堂教学探源及改进对策[J].湖北成人教育学院学报，2007，13（3）：7-9.

[5]许吉.高校课堂教学评价新模式及其特点的思考[J].黑龙江教育學院学报，2018，37（11）：44-46.

[6]李伟军.黄理裕.高校课堂教学质量动态评价研究[J].新课程研究（中旬刊），2018，01：24-26.

[7]张殿旭.故障树法在环境风险评价中的应用[J].油气田地面工程，2012，31（4）：23-24.

[8]刘坚，陈俊煌，夏百战，等.区间模型下声子晶体的带隙优化研究[J].振动与冲击，2018，37（17）：115-121.

[9]张雷雷，贺一雄，翟伟昊，等.基于超椭球模型的飞机液压刹车系统故障树分析[J].机械强度，2017，39（4）：842-847.

[10]操凤萍，樊  要.基于自适应蒙特卡洛算法的实时定位研究[J].计算机工程，2018，44（9）：28-37.