一种基于本地分区的挖掘算法研究

韩天鹏　王峰

摘 要：在频繁项集挖掘中减少数据库扫描次数是核心工作之一.本文提出一种利用本地支持信息来计算频繁项集的改进分区方法，在此基础上只需对数据库扫描一次.由于改进算法不进行第二次数据库扫描，仅使用从分区获得的本地支持的原因，使得频繁项集的挖掘准确率有一定的误差，但实验结果表明，误差在可控范围内.改进算法与Apriori、FP-growth和Partition算法相比，总体时间复杂度得到降低;内存使用和数据库访问时间减少，有一定的优越性.

关键词：数据挖掘;频繁项集;Partition算法;FP-Growth

中图分类号：TP311  文献标识码：A  文章编号：1673-260X（2019）11-0057-05

1 引言

频繁项集挖掘技术是数据挖掘中重要的描述性技术，是分类，聚类，索引和关联规则生成[1]等算法核心求解过程.而关联规则生产的目的是使决策者能够理解交易数据项之间的关系从而获得决策的数据支持.关联规则中频繁项目集挖掘的应用非常广泛[2]，如无线自组织传感器网络（WASN）中的服务质量改进[3]，实时心电信号分析和诊断[4]，印度夏季风降雨预测[5]，库存和利润管理[6]，自动网络监控[7]等.

Apriori算法[8]是频繁项集挖掘的经典方法.尽管Apriori算法很受欢迎，但它具有以下缺点：（1）从二级存储设备读取/写入数据时的I/O开销，与最大频繁项目集的大小成比例.（2）不可扩展具有大量项目的交易数据，因为它需要生成更多候选项集.（3）不能利用底层计算基础结构的并行处理能力.

为了克服Apriori算法的问题，许多研究提出了多样化思想的方法.例如：动态项目集计数（DIC）算法[9]，尝试通过同时计算不同长度项集的支持，对项目集的支持的训练模型来减少I/O操作的次数.Pincersearch算法[10]自下而上和自上而下的方向上搜索频繁项目集，在读取数据库时，除了计算对apriori等较小项集的支持外，它还计算候选最大频繁项集的支持，以减少数据库传递（I/O）的数量.如果最大的频繁项集很长，它会显著降低I/O开销.虽然DIC和Pincersearch算法在一定程度减少了I/O操作的数次数，并显著地提升了I/O的开销效率，但由于其不可扩展性，它们对于大型数据库来说是不适用的[11].

分区算法[12]基于一种新的思想，即创建适合主存储器的水平数据分区.在数据库扫描方面，它比apriori和其他相关方法有了显著的改进.但是，它会受到以下影响：（1）数据库I/O开销，因为它读取数据库两次以计算频繁项集.（2）时间复杂度更高，因为它从分区中计算更多的频繁项集.分区算法所需的额外数据库扫描是由于没有利用分區中计算的本地支持来生成全局频繁项集.此外，为了在不生成候选项集的情况下计算频繁项集，提出了fp-growth算法[13]，它对数据库进行两次扫描，但其生成的树不适合存储较大的数据库.eclat[14]在计算频繁项集之前，将数据从水平格式转换为垂直格式.尽管它只读取一次数据库，但它假定垂直数据库适合内存，该假设对于较大的数据库是无效[15].

在本文中，通过提出一个有效的分区算法，该方法只读取一次数据库来降低总体时间复杂度和内存使用率.利用分区中可用的局部支持信息，提高算法的效率.

2 频繁项集挖掘的划分算法综述

分区算法的核心思想是从每个数据分区计算局部频繁项集，然后通过第二次扫描数据库计算局部频繁项集的支持度来计算全局频繁项集.算法如下：设事务数据库D，其中包括N个事务，d个项.设I={i1，i2，…，id}为项集.

（1）创建m（≥2）个数据分区，d1，d2，…，dm来自一个包含n个事务的数据库D，其中包含d个项，使得每一个分区数据库Di，i=1，2，…，m都适合内存.这里，Di是包含d个项，N/m个事务的一个分区.

（2）计算本地频繁项集.对于每个分区，Di（i=1，2，…，m）使用apriori算法计算本地频繁项集.

（3）计算全局频繁项集.

（a）结合在第二步中获取的本地频繁项集.

（b）通过读取数据分区Di（i=1，2，…，m）计算每个本地频繁项集的支持生成全局频繁项集.

分区算法执行两次数据库扫描并计算m组本地频繁项集，并且各分区中生成一个本地频繁项集.

3 基于局部支持的频繁项集挖掘分区算法（LPFM）

在本节中，提出了一种有效的分区算法来计算频繁项集，算法如下：

3.1 算法

输入：

（1）事务数据库D，具有N个事务和d个项目，（2）本地支持阈值，（3）全局支持阈值，输出：频繁项目集G.

算法如下：

算法1 创建分区数据库.将事务数据库D逻辑划分为m（≥2）个数据分区，D1，D2，...，Dm，每个都有N/m个事务和d个项目，这样每个分区都适合内存.D=D1∪D2∪…∪Dm，并且Di∩Dj=？覫，？坌i，j都有i≠j.

算法2 对于每个分区，Di，i=1，2，...，m，计算本地频繁项目集.

（1）将分区Di从辅助存储设备读取到内存中.

（2）[Fi，Si]←计算本地频繁集sets（Di，ε，θ）.

其中Fi是本地频繁项集的集合，Si是Fi的支持度.使用FP-Growth算法从Di中计算

本地频繁项目集.

算法3 计算全局频繁项集G.初始化G←？覫

（1）计算本地频繁项集：F=F1∪F2∪…∪Fm.每个本地频繁项集f∈F，执行以下操作：

（2）计算f的本地支持：S（f）←∑si（f）

（3）计算{F1，F2，…，Fm}中f的出现频率，r（f）←基数{Fi|f∈Fi，i=1，2，…，m}.r（f）表示f频繁出现的分区数.

（4）检查f是否为全局频繁项集.if（S（f）≥θ），then G←G∪f.

（5）检查f是否为非全局频繁项集.else if [S（f）+（m-r（f））*（ε-1）]<θ，否则，丢弃f.

（6）检查f是否可能是全局频繁项集.else if [S（f）+（m-r（f））*（ε-1）/2]≥θ， then G←G∪f.

（7）其他情況丢弃f.

使用FP-Growth算法的思想枚举局部频繁项集以降低计算时间复杂度[步骤2（2）].所提出的算法的主要改进在于，计算全局频繁项集时，避免了数据库的二次扫描（步骤3）.在步骤3（2）中，针对每个本地频繁项集合，聚合所有来自m个分区的本地支持.基于这种本地支持，本地频繁项集f可以分类如下：

（1）全局频繁项集，如果满足全局阈值θ[步骤3（4）].

（2）非全局频繁项集[步骤3（5）]，如果不满足全局阈值θ;对于f不频繁的（m-r（f））个分区，考虑ε-1的最大可能支持关.

（3）可能的全局频繁项集[步骤3（6）]，如果它满足全局阈值θ，则在计算f不是频繁的（m-r（f））分区中（ε-1）/2的平均支持度后.由于在不频繁的分区中f的支持信息不可用，因此它的支持近似为平均支持度（ε-1）/2，以确定它是否可能是全局频繁项集.

本文所提算法的局限性在于它可以将一些频繁项集分类为非频繁项和子频繁项集，反之亦然.但是，它通过步骤3（6）中的平均度可以最大程度减少这种错误分类.

3.2 举例说明

用表1所示的数据库作为例库来说明所提出的算法.假设使用事务T1到T10、T11到T20和T21到T30创建了3个分区.所提出的LPFM方法的逐步分析如表2所示.本地支持和全局支持阈值固定为30%.该方法得到的频繁项集和分区算法分别见表2和表3.同时观察到，从这两种方法获得的频繁项集与表2和表3所示相同.

4 算法分析

在本节中，将比较Apriori，Partition和FP-Growth算法在数据库I/O开销（即数据库扫描数量）和计算方面时间复杂性的性能.

4.1 数据库扫描分析（I/O开销）

由于大量的交易数据存储在二级存储设备上，如磁盘，所以频繁项目挖掘中最耗时的活动之一是扫描存储在辅助设备上的数据库.因此，最小化数据库扫描的数量是一项至关重要且具有挑战性的任务.

在Apriori算法中，数据库扫描的次数s（s≥2）与最大频繁项集的大小成比例.Apriori算法为频繁项集的每个级别读取数据库，算法数据库扫描数RA=s，数量极巨大.

分区算法Partition将数据库扫描的数量减少到2.第一次读取数据库计算本地频繁项集.第二次读取数据库时计算全局频繁项集.因此，Partition算法数据库扫描数RP=2.

FP-Growth算法执行第一次数据库扫描计算频繁的1项集.随后，第二次读取数据库构建FP树并生成频繁项集.FP-Growth算法扫描次数RG=2.

此外，本文提出的LPFM方法仅扫描数据库一次，使用FP-Growth算法计算本地频繁项目集.然后，利用本地支持信息生成全局频繁项集.LPFM算法数据库扫描数RL=1.

Apriori，Partition，FP-Growth和LPFM方法所需的数据库读取/扫描次数如表4.

4.2 时间复杂度分析

就计算时间而言，很明显LPFM算法与Apriori和Partition算法相比显示效率提高了，与FP-Growth算法在一个数量级上.

5 实验结果与分析

5.1 使用的数据库和实验设置

实验使用来自频繁项目集挖掘数据集存储库的两个数据集.这两个数据库每个包含100，000条事务.每个事物是集合项目的子集{1，2，3，...，1000}.这两个数据库的主要区别在于交易长度.第一个数据库具有较少数量的项目，平均值为10，第二个数据库显示具有更多项目的交易，平均值为39.6.这两个数据库是具有较大的数据库和不同的项目分布.

实验配备Intel i3处理器，8GBRAM，1TBHDD和Ubuntu16.04的计算机系统上运行.实验使用Python脚本来实现FP-Growth算法.LPFM分区算法，创建了5个分区，每个分区具有相同数量的事务.

生成频繁项目集的支持阈值对于第一个数据集固定为1%，第二个数据集固定为5%.由于第一个数据库中的事务长度较小，将支持阈值设置为1%以获得频繁项目集的合理数量.第二个数据库将支持阈值设置稍高为5%，这样可获得高密度交易具有较低阈值的更频繁的项目集.

5.2 实验分析

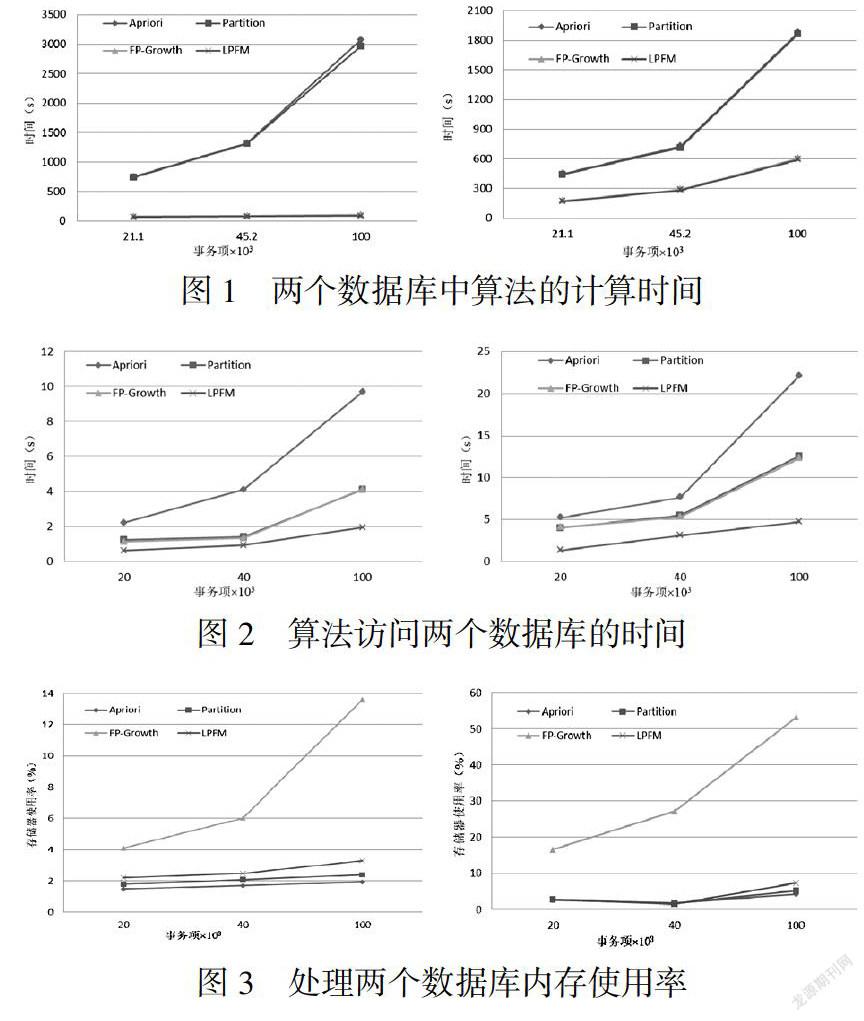
实验表明，LPFM与Apriori算法就数据库开销方面，LPFM算法优于Apriori.与Apriori方法（图1）相比，LPFM的计算时间更短.另外，与Apriori方法相比，LPFM需要更低的数据库访问时间（图3）.因此，LPFM方法在计算时间和数据库开销方面显示出优于Apriori的优势.

由于LPFM算法仅扫描数据库一次，而Partition算法扫描两次，LPFM算法应更优.实验分析证实了这一点（图3）.实证结果表明，两个数据集中LPFM算法比Partition算法的性能更优（图2）.因此，与分区算法相比，所提出的LPFM在数据库开销和计算时间复杂度方面更优.

LPFM与FP-Growth算法相比，LPFM将数据库扫描的数量减少到1，而FP-Growth算法需执行两次数据库扫描.因此，LPFM的数据库访问时间比FP-Growth方法低（图3）.LPFM利用FP-Growth方法的思想来计算局部频繁项集，所以它在计算时间方面与FP-Growth算法相比具有竞争力（图2）.FP-Growth算法用FP-tree来压缩整个数据库，所以消耗内存更多.而LPFM使用了分区本地的较小FP-tree，所以消耗更少.实验结果表明LPFM方法相对于FP-Growth在内存使用方面提高了很多（图4）.

计算与Apriori，FP-Growth和Partition算法几乎相同数量的频繁项目集.LPFM分别找到370和299个频繁项集，而其他三个算法分别获得386和316个频繁项集.频繁项目集数量的不同是由于LPFM不進行第二次数据库扫描，仅使用从分区获得的本地支持的原因.LPFM方法需要一次数据库扫描，而其他3种算法至少需要2次数据库扫描.

与Apriori和Partition算法相比，LPFM方法可扩展，数据库可动态变化增加，同时总体时间复杂度随着数据库的变化而变化.此外，LPFM方法比FP-Growth算法显示出有竞争力的计算时间，减少内存的使用和数据库访问时间.

6 结论

本文提出了一种新的频繁项挖掘分区方法，利用本地支持信息生成全局频繁项集.方法仅扫描数据库一次，并且与Apriori，Partition和FP-Growth算法相比，实验结果表明，挖掘算法的性能有了显著的提高.由于所提出的分区思想方法，可以在诸如Hadoop的并行计算环境中容易实现，所以算法所产生的频繁项集，更接近于分区算法.

参考文献：

〔1〕Han J， Cheng H， Xin D， et al. Fequent pattern mining：current status and future directions[J]. Data Mining Knowledge Discover，2007， 15（1）：55–86.

〔2〕Zaki M J. Parallel and distributed association mining： a survey[J]. IEEE Concur，1999 7（4）：14–25.

〔3〕Boukerche A， Samarah S. A novel algorithm for mining association rules in wireless ad hoc sensor networks[J]. IEEE Transactions on Parallel and Distributed Systems，2008， 19（7）：865–877.

〔4〕Gu X， Zhu Y， Zhou S， et al.  A real-time fpga-based accelerator for ecg analysis and diagnosis using association-rule mining[C]// ACM Transactions on Embedded Computing Systems， 2016 15（2）：25：1–25：23.

〔5〕Vathsala H， Koolagudi S G. （2017） Prediction model for peninsular indian summer monsoon rainfall using data mining and statistical approaches[J]. computer geosciences，2017， 98：55–63.

〔6〕Kim J S. Emotion prediction of paragraph using big data analysis[J]. Journal of Digital Con-vergence，2016， 14（11）： 267–273.

〔7〕Qu Z， Keeney J， Robitzsch S， et al. （2016） Multilevel pattern mining architecture for automatic network monitoring in heterogeneous wireless communication networks[J]. China Communication[J] ，2016，13（7）：108–116.

〔8〕Agrawal R， Srikant R. Fast algorithms for mining association rules in large databases[C]// Proceedings of the 20th international conference on very large data bases， VLDB， Santiago，Chile， 1994， 487–499.

〔9〕Bhandari A， Gupta A， Das D.Improvised Apriori Algorithm using frequent pattern tree for real time applications in data mining[J]. Procedia Computer Science， 2015，46：644–651.

〔10〕Lin Di， Kedem Z M. Pincer-search： an efficient algorithm for discovering the maximum frequent set[J]. IEEE Transaction Knowledge Data Engineering，2002， 14（3）：553–566.

〔11〕Han J， Pei J， Yin Y. Mining frequent patterns without candidate generation[C]// Proceedings of the 2000 ACM SIGMOD international conference on management of data， ser. SIGMOD’00. ACM， New York， NY， 2002， 1–12.

〔12〕Jung H， Chung K. Life style improvement mobile service for high risk chronic disease based on PHR platform[J]. Cluster Computing， 2016，19（2）：967–977.

〔13〕韩天鹏，白玲玲，王浩.基于候选项集剪枝的Apriori算法的研究[J].阜阳师范学院（自然科学版），2014，31.

〔14〕曹莹，苗志刚.基于向量矩阵优化频繁项的改进Apriori算法[J].吉林大学学报（理学版），2016，54（2）：349-353.

〔15〕刘云，向禅.基于虚构理论对不平衡数据集中少数类关联规则挖掘的研究[J].云南大学学报（自然科学版），2017，39（4）：33-38.