考虑数据时效性的高效KNN算法
王轶凡




摘 要:本文在K-近邻(KNN)算法中考虑数据时效性,在数据时效性的一系列假设下,通过蒙特卡洛模拟方法根据接受概率函数剔除训练集中时效性差的数据.最后通过对北京市二手房成交价格数据分析,表明方法在对存在时效性的数据的问题上,在预测准确率及算法时间上都有良好表现,具有广泛的应用价值.
關键词:KNN算法;数据时效性;蒙特卡罗模拟
中图分类号:TP311.13 文献标识码:A 文章编号:1673-260X(2019)11-0019-03
1 引言
Cover和Hart(1967)提出的KNN算法是统计机器学习中的经典算法之一,是一种简单且高效的非参数分类或估计算法.KNN算法是一种“消极”学习方法,所谓的“学习”过程仅仅是将数据集存储下来,在每一次的分类或回归过程中,都需要计算带预测样本与所有训练数据的距离,计算的时间复杂度为O(D×N),其中D是样本属性维度,N是训练集样本量.为了使算法稳定有效的,通常情况下有D<<N,所以训练集样本量N的大小对算法效率有重要的影响.对此,诸多研究者通过从全部训练样本集中选择出部分样本,例如Hart(1968)提出的压缩最近邻法(Condensed Nearest Neighbor)和Gates(1972)提出的约减最近邻法(Reduced Nearest Neighbor),他们的核心思想都是通过选择性质良好的训练样本子集,在不失算法有效性的前提下,降低训练集样本量N的大小,从而提高KNN算法的效率.
大数据时代,特别是积累了大量的时间序列数据,从而为分析研究提供了更加丰富的资源.但并不是在所有情况下,时间越长,越有利.李默涵,李建中和高宏(2012)指出数据的时效性是影响数据质量的重要因素之一,时效性差的数据对数据分析结果有许多不利影响.然而,大部分KNN算法的研究中,少有对数据的时效性的讨论.大多KNN算法的研究对于有时间属性的数据都假定在观测时间内,样本的分布不随时间变化,然而这种假设往往不符合实际.
本研究使用改进的KNN算法,在对数据的时效性的一系列假设下,以保留时效性好的数据为依据,剔除训练集部分数据,从而在提高数据分析结果准确性的同时,提高KNN算法的计算效率.
本文剩余章节安排如下:第2节介绍普通的KNN算法;第3节介绍本文提出的考虑数据时效性的高效KNN算法,其中3.1小节对数据的时效性进行一系列假设,3.2小节推导了训练集选择的接受概率函数,3.3小节介绍具体算法;第4节对北京市二手房成交价格数据进行实证分析,对比KNN方法与本文方法预测结果;第5节是本文的结论与讨论.
2 KNN算法介绍
假设有训练数据集{X(i),Y(i)}i=1,…,N,其中每个样本{X(i),Y(i)}有D维属性X(i)=(x1(i),x2(i),…,xD(i))以及一个属性值(或类别标号) Y(i)=y(i).对于待预测的样本点X(i),定义其与训练集样本点{X(i),Y(i)}的属性距离为欧式距离(也可以是任何意义上的距离):
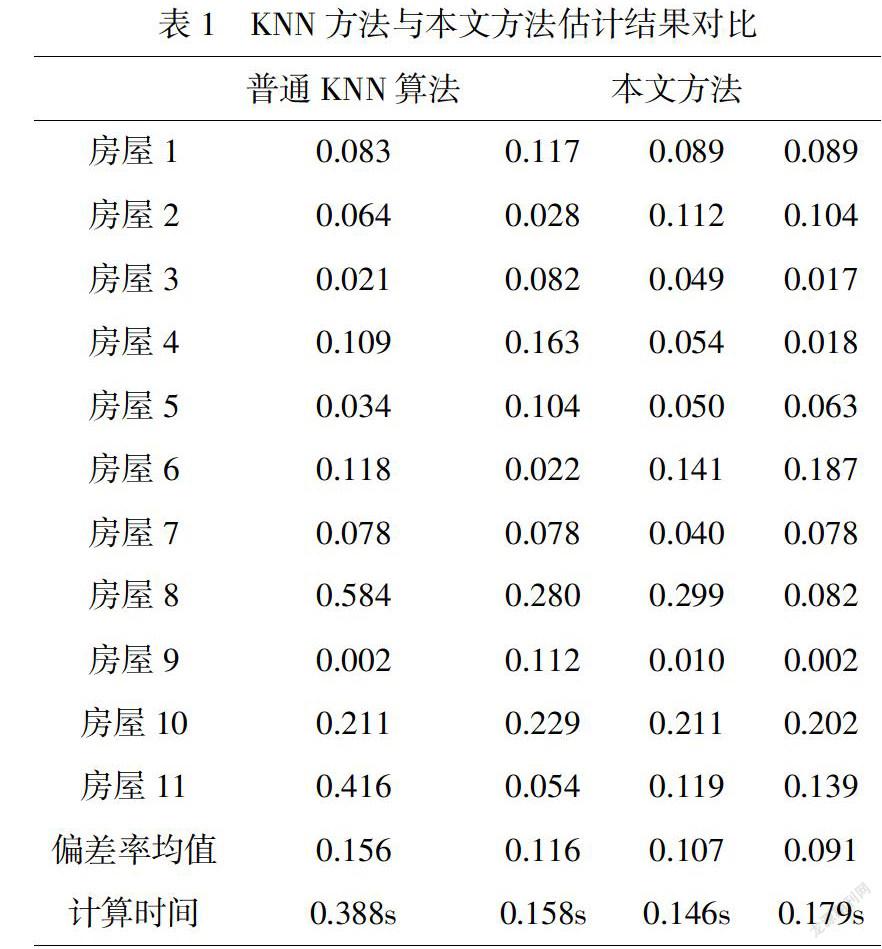
普通KNN算法与本文方法对比结果见表1.表1报告了普通KNN算法及本文方法对2019年6月3日的11个二手房估计结果的偏差率(偏差率=(实际值-理论值)/理论值),由于本文方法选取训练集基于蒙特卡洛模拟,每次选取的训练集可能不同,导致估计结果有差异,所以表1报告了3次本文方法的结果以便比较.此外,算法的计算时间也报告在表1中.
观察表1我们由如下几点发现:
(1)本文方法3次对11个房屋的预测中,每次的预测结果有差异但差异较小.相较于普通KNN算法,本文方法预测结果在有的房屋的预测偏差率更好,而在有的房屋的预测偏差率更差,但在预测偏差率均值上,本文方法的3次结果都优于普通KNN方法,可以说明在考虑了数据时效性后,预测结果更准确.
(2)从计算时间上看,本文方法的3次结果用时均小于普通KNN方法,低于普通KNN方法用时的一半.这是由于对训练集进行选择剔除后,训练集样本量N降低,计算复杂度降低.值得一提的是,本文方法报告的计算时间不仅包括预测过程用时,还包括选择训练集用时.本文方法交普通KNN算法更高效.
(3)考虑房屋8和房屋11的预测结果,普通KNN方法偏差率分别为0.584和0.416,即预测值较真实值相差大约50%,预测效果很差.而本文方法对房屋8的3此预测偏差率分别为0.280,0.299,0.082,相较0.584有很大改善,对房屋11的预测偏差率分别为0.054,0.119,0.139,相较0.416有很大改善.这可能是由于本文方法剔除了时效性差的数据,使得预测结果更加准确.
综上分析,我们认为,本文提出的考虑数据时效性的高效KNN算法能在提高数据分析结果准确性的同时,降低KNN算法的计算时间.
5 讨论
本文在KNN算法的基础上,对数据的时效性进行一系列假设,并在假设的基础上推导出训练集接受概率函数,并提出通过蒙特卡罗模拟方法选择新的训练子集,再用新的训练集进行KNN算法的改进.随后,我们将本文方法应用到北京市西城区二手房成交价格数据的实证研究中.分析显示,本文方法能在提高数据分析结果准确性的同时,降低KNN算法的计算时间.
值得一提的是,由于本文实证旨在比较KNN算法和本文方法,属性的选择较为随意,并没有进行详细的影响因素分析,这导致预测结果的偏差率并不十分理想.如果详细分析影响因素或使用加权KNN方法,可以得到更完美的预测结果.这值得进一步研究.
参考文献:
〔1〕Cover T M , Hart P E . Nearest Neighbor Pattern Classification[J]. IEEE Transactions on Information Theory, 1967, 13(1):21-27.
〔2〕Hart P E . The condensed nearest neighbor rule[J]. IEEE Trans. Inf. Theory, 1968, 14(3):515-516.
〔3〕Gates G W . The reduced nearest neighbor rule (Corresp.).[J]. Information Theory IEEE Transactions on, 1972, 18(3):431-433.
〔4〕李默涵,李建中,高宏.数据时效性判定问题的求解算法[J].计算机学报,2012,35(11):2348-2360.
〔5〕周湘,袁文,李汉青,et al.北京市二手房价格时空演变特征[J].地球信息科学学报,2017(8).

