基于GTM和多分辨率B样条的医学图像配准方法

于佳 张兴伟

摘  要：本文提出了一种基于GTM（Graph Transformation Matching）和多分辨率B样条的医学图像配准方法。为了得到精确的特征点对，使用GTM算法去除血管树模型中的冗余点;然后使用多分辨率B样条函数对图像进行配准。肝脏MRI上的实验证明，本文提出的非刚性配准方法能够有效提取出特征点，并且达到了较好的配准精度。

关键词：医学图像配准;GTM;多分辨率B样条

中图分类号：TP391.41      文献标识码：A 文章编号：2096-4706（2019）15-0085-04

Medical Image Registration Method Based on GTM and Multi-resolution B-splines

YU Jia1，ZHANG Xingwei2

（1.School of Computer and Information Engineering，Luoyang Institute of Science and Technology，Luoyang  471023，China;

2.Luoyang Laipson Information Technology Co.，Ltd.，Luoyang  471003，China）

Abstract：This paper proposes a Graph Transformation Matching （GTM） and multilevel B-splines based approach for medical image registration. We utilize GTM algorithm to remove outliers to get the accurate pair-wise feature points. Then Multilevel B-Splines algorithm is used to find the non-linear transformation between  two images. Experiments on liver MRI show that the proposed non-rigid registration method can effectively extract feature points and achieve better registration accuracy.

Keywords：medical image registration;GTM;multilevel B-splines

0  引  言

隨着医学影像学的不断发展，医学影像分析在疾病诊疗中占据越来越重要的位置，成为临床诊断中一项非常重要的内容。20世纪以来，医学成像技术日新月异，各种高科技成像设备层出不穷。不同成像技术可以对同一器官分别提供结构信息和功能信息，这些信息互为补充，医生临床诊断时，需要首先使这些图像信息坐标达到空间上的一致，将这些信息融合成一个新的图像显示出来，这一过程称为图像配准。医学图像配准是指寻找一种空间变换，使不同图像上的对应点达到空间位置上的一致。医学图像配准是医学图像处理的一个重要环节，它可以校正病人多次成像间的位置变化以及由于成像模式本身导致的畸变;对同一个病人的不同时间的图像进行配准，可以了解器官的变化情况;对不同的人的图像进行配准，可以形成疾病或人群特异性图谱，用于正常与否的分析。因此，医学图像配准是医学图像融合、医学图像重建、图像与标准图谱的匹配的基础，近年来，它已成为医学图像处理领域中的热门研究方向之一。

图像配准算法分为特征驱动和灰度驱动两大类。基于特征驱动的算法首先提取源图像和目标图像之间的一些共同特征，建立特征之间的对应关系，从而提取出特征点对，实现图像的配准。常用的特征有图像的轮廓边缘、角点、曲率、表面斑纹[1]等。

冯林等[2]提出了一种基于分层互信息和薄板样条自动确定特征点的方法，但该算法由于依赖灰度统计相关性，很难取得足够多的标记点。

Rohr等[3]考虑使用薄板样条函数作为变换模型，使用B样条函数来模拟弹性形变，并且通过调整控制点的位置来计算匹配后的形变场。

基于灰度驱动[4-6]算法直接对图像灰度进行操作，利用图像的灰度信息，建立两幅图像的相似性度量，然后使用某种优化算法，确定变换模型参数，使相似性度量达到最大值。

常用的灰度驱动方法有Christensen等[7-9]提出的基于粘流体变换的方法和F.Maes[10]等提出的粘滞流体模型。利用图像灰度信息进行配准，提高了配准的精度和鲁棒性，但具有计算量大、速度较慢的缺点。

本文提出了一种基于GTM（Graph Transformation Matching）和薄板样条的非刚性配准方法，使用联合图算法进行特征提取，使用改进的GTM算法去除冗余点，达到精确提取特征点对的目的，在此基础上，构造三次B样条曲面函数进行配准。实验证明，本文提出的方法在肝脏MRI图像上达到了较好的配准结果。

1  基于GTM算法的特征点提取与优化

特征空间的选择是非刚性医学图像配准中一个非常重要的步骤，准确提取图像特征可以降低计算复杂度，提高图像配准精度。本节介绍一种基于联合图算法的自动特征提取方法，通过提取肝脏血管中的点特征和线特征，采用深度递归策略建立肝脏血管中的血管树模型，在此基础上采用GTM算法进行冗余点去除，提取图像中精确特征。

1.1  血管树的建立与配准

肝脏中存在大量的血管，其位置和长度都可能发生变化，但是他们的结构特征近乎固定，因此我们可以把这些血管的形状作为一个具有很强鲁棒性的特征，从这些树形结构的血管中自动并且准确地提取出特征点。最简单有效的血管提取方法是对图像取阙值，然后得到二值图像。

在经过二值化的图像中，存在血管的像素点值为1，背景点像素值为0，我们用结点来表示血管的像素点。为了便于后续血管树的匹配，我们需要在结点结构中存储足够多的结点信息，包括左孩子域、右孩子域、双亲节点域、像素值域、结点层次域、与结点相连边长度域等，其中结点层次域和与结点相连边长度域是根结点和分支结点所特有的，其他结点域值为0。建立起特征树后，我们就可以对树进行遍历等操作，取得结点的度、层次、边的长度等信息，在此基础上，使用联合图算法对血管树进行配准，具体算法如下。

树联合图的定义如下：

T1=（V1，E1，r1），T2=（V2，E2，r2），T1和T2是两棵树，V1和V2分别是其结点的集合，E1和E2分别是其边的集合，它们的根分别为r1和r2。定义联合图G=（VA，EA）且满足以下条件：

条件一：

VA={va∈V1×V2|∑wi fi（va）≥0.5}           （1）

wi∈[0，1]，wi=1

条件二：

EA={（va，vb）∈VA×VA|∑vf gj（va，vb）≥0.5} （2）

vi∈[0，1]，vf =1

其中，va=（va1，va2）∈VA，va1和va2代表两棵树中可能的对应点对，VA是从V1到V2可能存在映射关系的点对集合，对这个点对进行相似度测量，测量值的范围在0和1之间。数值越接近1，点对的相似度越大，反之越小。因为有多种不同的相似度测量方法，且每种方法都不一定是决定性的，因此对每一个方法乘以一个权值wi∈[0，1]，且wi=1。如果一个结点va所有方法与权重的乘积的和大于等于0.5，则认为这两个结点存在映射关系，即va=（va1，va2）∈VA。

对va=（va1，va2），vb=（vb1，vb2），va与vb之间存在一条边e的条件是：

条件一：

va1↔vb1之间存在映射关系，va2↔vb2之间存在映射关系。

条件二：

在V1中，va1与va2之间存在一条边，V2中，vb1与vb2存在一条边。

1.2  基于GTM算法的冗余点去除

P={pi}和P´={}是大小为N的两幅图像特征点的集合，并且两个集合的特征点之间已经初步建立起了一对一的映射关系（pi与一一对应）。GTM算法的最终目的是找出两幅图像中错误的映射关系，并且分别从两个集合中删除相应的冗余点。为了迭代去除错误映射，首先对原始图像建立中值K-NN图Gp=（Vp，Ep），构建过程如下：

（1）对集合中的任意点pi建立相应顶点vi，Vp=v1，

…，vn。

（2）若pj是pi的K近邻点，且‖pi-pj‖≤η，则在顶点i和j之间连接一条边。

η=‖pl-pm‖

对图Gp建立一邻接矩阵Ap，当（i，j）∈Ep时，Ap（i，j）=1，否则Ap（i，j）=0，同样对于=（，）建立邻接矩阵，Ap和 都为N×N的矩阵。计算R=|Ap-|， jout=argmaxR（i，j），j列在两幅图像中产生了最多的不同边。点对（Vjout，）为结构上的冗余点。

在实现的过程中，寻找K近邻可以发现数据的计算量非常大，因此可以采用快速搜索近邻法对算法进行改进。其基本考虑是将样本分级成一些互不相交的子集，并在子集的基础上进行搜索。

2  基于多分辨率B样条的弹性配准方法

在上节提取出特征点的基础上，构造一个标准的双三次B样条曲面，为了使逼近的精度和曲面的光滑性得到平衡，对网格进行分级，在每一级控制网格的作用下产生逼近函数。这一过程由最稀疏的控制网格开始，递增到最密的控制网格，最后将各级逼近函数相加得到最终的逼近函数。根据确定后的变换函数对待配准图像进行空间变换操作，然后得到配准后的图像。

多分辨率B样条的提出，是为了解决曲面光滑性和逼近精度的平衡问题，其基本原理是将控制网格分级，使密度由最小的一级逐渐过渡到最大的一级。

假设覆盖于2包含点集{（xi，yi）}的矩形域Ω上控制网格的序列为Ф0，Ф1，…，Фk。Ф0是由（m+3）×（n+3）个控制顶点所组成的控制网格，其顶点的分布密度是确定的，其他级控制网格的控制顶点的间距是由前一级控制网格间距二分得到。如果第Фk的控制顶点数为（m+3）×（n+3），则第k+1级控制网格Фk+1的控制顶点数是（2m+3）×（2n+3）。算法从控制网格Ф0开始，在Ф0的作用下产生逼近函数F0。求出F0在点（x，y）处的值F0（x，y），其值与点（x，y）在数据点集中的z坐标之间的差为Δ1z=z-F0（x，y）;下一级控制网格Ф1产生函数F1，F1逼近点集，Ω1={（x，y），Δ1z}，即F1在点（x，y）处的值逼近Δ1z。点（x，y）和它在原数据点Ω中的z坐标值，F0+F1的误差为Δ2z=z-F0（x，y）-F1（x，y），Δ2z小于F0产生的误差Δ2z。对第k级，控制网格Фk产生逼近函数Fk，Fk逼近Δkz，Δkz=z-Fi（x，y）=Δk-1z-Fk-1（x，y），且Δ0z=z。这个过程由控制网格Ф0开始，一致遞增到控制网格Фk。最后逼近函数F为各级函数Fk的和。

在多分辨率B样条逼近中，控制网格所包含的控制顶点数称为控制网格的分布密度。控制网格Фk的分布密度是（m+3）×（n+3）。当控制顶点较稀疏时，函数的形状比较光滑，但逼近精度低，而当控制顶点分布密度足够高时，逼近精度很高。

3  实验结果

为了验证本文所提出的算法，使用了一对大小为256像素×256像素的肝脏MRI图像，像素的大小是1mm×1mm。为了验证去除冗余点的效果，文本使用Soft Assign算法、RANSAC算法、改进的GTM算法在不同比例条件下重复计算出平均精确度，精确度越高，则表示冗余点去除效果越好。

从表1可以看出，改进的GTM算法和RANSAC算法运算结果相似，Soft Assign算法的运算结果相比改进的GTM和RANSAC相差很多。改进的GTM算法比RANSAC算法的准确度略好一些，特别是在冗余点比例比较大的情况下，可以很明显地看出改进的GTM的精确度要好于RANSAC。

从这个实验结果图中可以发现改进的GTM算法的精确度较高，这对一些应用，特别是对求解空间变换函数的应用是十分重要的。

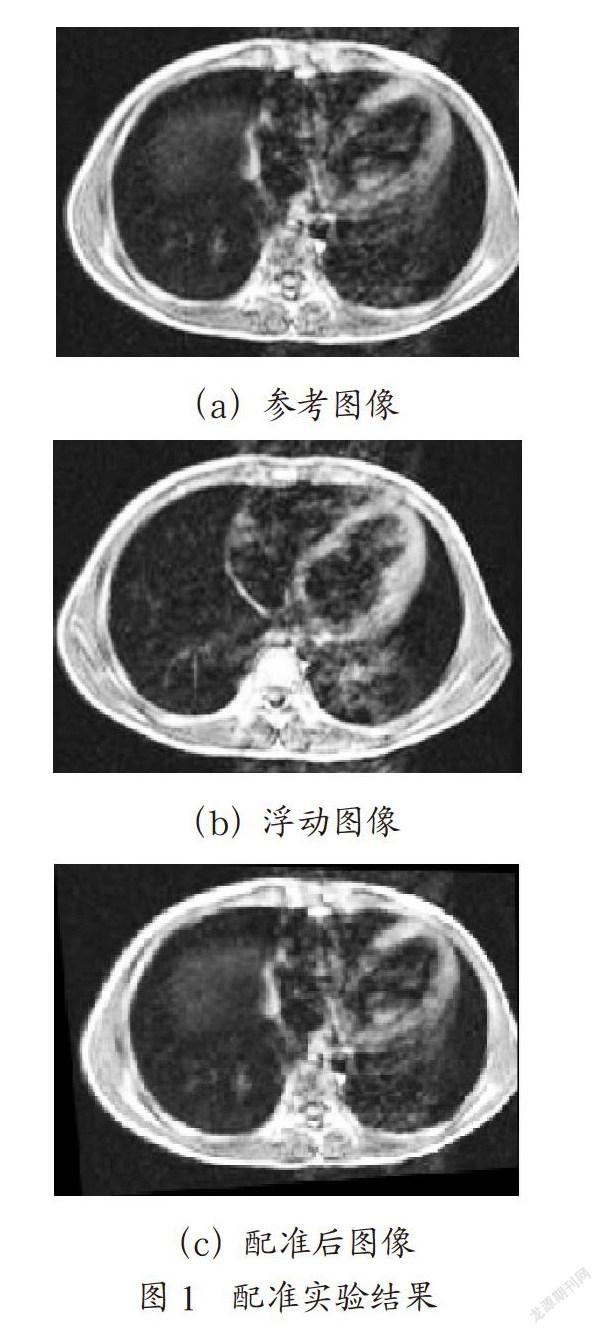
本文采用互信息量对配准结果进行验证，值越大表示配准结果越精确。如图1所示，图1（a）是有一定形变的肝脏MRI参考图像，图1（b）是肝脏的MRI浮动图像，图1（c）是最终的配准结果。由图可以看出，配准后，参考图像（a）与配准后的图像（c）已基本完全一致了。

经过计算图像的信息量得到：（a）与其自身的互信息量为3.59，（a）与（b）的互信息量为1.02，图1（a）与图1（c）的互信息量为3.56，由此可以看出，经过非刚性配准后，图像达到了比较好的配准精度。

4  结  论

本文提出了一种基于GTM和多分辨率B样条的医学图像弹性配准方法。针对肝脏器官存在大量血管结构的特点，使用自适应阈值对血管树形态进行建模，使用GTM算法对冗余点进行有效去除，最后使用多分辨率B样条插值方法对图像进行配准。肝脏MRI的实验结果证明，本文提出的方法能够有效提取特征点，达到了较好的配准结果。

参考文献：

[1] Can A，Stewart C V，Roysam B，et al. A feature-based，robust，hierarchical algorithm for registering pairs of images of the curved human retina [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24（3）：347-364.

[2] 冯林，张名举，贺明峰，等.用分层互信息和薄板样条实现医学图像弹性自动配准 [J].计算机辅助设计与图形学学报，2005（7）：1492-1496.

[3] Rohr K，Stiehl S H，Sprengel R，et al. Landmark-Based Elastic Registration Using Approximating Thin-Plate Splines [J].IEEE Trans. Med. Imaging，2001，20（6）：526-534.

[4] Rueckert D，Sonoda L I，Hayes C，et al. Nonrigid Registration Using Free-Form Deformations：Application to Breast MR Images [J].IEEE Transactions on Medical Imaging，1999，18（8）：712-721.

[5] Niu C. Medical Image Registration Based on Mutual Information Using Kriging Probability Density Estimation [J].Conference proceedings：Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Conference，2005，3：3097-3099.

[6] Liu J，Tian J，Dai Y. Multi-modal medical image registration based on adaptive combination of intensity and gradient field mutual information [J].Conference proceedings ：Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Conference，2006：1429-1432.

[7] Christensen G E，Rabbitt R D，Miller M I. Deformable templates using large deformation kinematics [J].IEEE Transactions on Image Processing，1996，5（10）：1435-1447.

[8] Christensen G E，Miller M I，Vannier M W，et al. Individualizing neuro-anatomical atlases using a massively parallel computer [J].Computer，1996，29（1）：32-38.

[9] Lester H，Arridge S R，Jansons K M，et al. Non-linear Registration with the Variable Viscosity Fluid Algorithm [A].Proceedings of International Conference on Information Processing in Medical Imaging [C].Berlin：Springer，1999：238-251.

[10] Hellier P，Barillot C. Cooperation between local and global approaches to register brain images [A].Proceedings of International Conference on Information Processing in Medical Imaging [C].Berlin：Springer，2001：315-328.

作者簡介：于佳（1980.10-），男，汉族，河南洛阳人，讲师，博士研究生，研究方向：医学图像处理、自然语言处理、机器学习;张兴伟（1981.06-），男，汉族，河南洛阳人，研究员，硕士研究生，研究方向：医学图像处理、大数据技术。