高中数学思想方法之分类讨论的研究
夏耀健

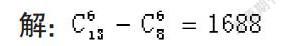
高中的数学学习,除要求学生学习数学知识外,还要培养数学的思想方法和意识,它不仅是数学的灵魂和精髓,还是学生对数学内容的本质认识和对所使用的方法和规律的理性认识。同时它可以有效地促进学生的深度学习,教师产生有深度的课堂氛围。
常见的数学思想方法:分类讨论思想、数形结合思想、化归和转化思想等。重视对这些思想方法的渗透运用,不仅有利于学生领悟数学的真谛,学会用数学思想思考问题,掌握解决数学问题的途径、策略,还能提高学生的核心素养、分析问题和解决问题的能力。
其中分类讨论思想是历年高考的必考内容,它不仅是高考的重点与热点,而且是高考的难点。每年在中档题或高档题中甚至在低档题中都设置分类讨论的题目,因为通过分类讨论的考查,可以推断学生思维的严谨性和分析问题、解决问题的能力。所以本文重点研究了分类讨论思想在高中数学常见题型中的应用,以便学生更加容易去理解和运用这种思想方法。
一、分类讨论的原则和一般步骤
1.分类讨论的原则
分类讨论思想是当问题的对象不能进行统一研究时,就需要对研究的对象按某个标准进行分类,然后对每一类分别研究,给出每一类的结论,最终集合各类结果得到整个问题的解答。实质上分类讨论就是“化整为零,各个击破,再集零为整”的数学思想。
科学的分类满足三个原则:(1)分类应按同一个标准;(2)分类应是完备的;(3)分类应是纯粹的。
2.分类讨论的一般步骤
(1)确定讨论的对象和所要讨论的取值范围;(2)合理分类:不重复、不遗漏、划分讨论只能按统一标准;(3)讨论应逐级进行,不能越级,逐类、逐段讨论;(4)最后归纳并得出结论。切记,能不分类的要尽量避免,决不无原则地去分类讨论,增加计算量。
二、分类讨论思想在高中数学
常见题型中的应用
1.根据数学的概念来确定分类标准
由数学概念而引起的分类讨论,概念分类整合即利用数学中的基本概念对研究对象进行分类,如集合的定义、绝对值的定义、不等式的转化、实系数一元二次方程的根的定义、直线的倾斜角等,然后分别对每类问题进行解决。解决此问题可以分解为三个步骤:分类转化、依次求解、汇总结论。汇总结论就是对分类讨论的结果进行整合,这个步骤很重要。
【例题】已知集合A={1.3. },
B={1,m},A∪B=A, 则m=( )
A.0或 B.0或3
C.1或 D.1或3
思路剖析:在集合的运算中要注意元素的无序性和互异性,元素与集合、集合与集合之间关系的分类讨论。
解:A∪B=A B A ∴m= 或m=3
m=0或1或3,经验m=1(舍)故选B
2.根据数学中的定理、公式和性质来确定分类标准
由性质、定理、公式的限制而引起的分类讨论:如函数的单调性、基本不等式、无穷等比数列各项和、等比数列{an}的前n项和公式等数学中的某些公式、定理、性质在不同条件下有不同的结论,在运用它们时,就要分类讨论,分类的依据是公式中的条件。
3.根据运算的需要确定分类标准
由数学运算要求而引起的分类讨论:如除法运算中除数不为零,偶次方根为非负数,对数运算中真数与底数的要求,指数运算中底数的要求,不等式中两边同乘以一个正数、负数,三角函数的定义域等。
【例题】(2011上海高考)已知函数f(x)=a·2x+b·3x,其中常数a,b满足ab≠0。
(1)若ab>0,判断函数f(x)的单调性;(2)若ab<0,求f(x+1)>f(x)时x的取值范围。
思路剖析:此题的第1小题运用函数的单调性,对a,b同号及异号进行讨论,而第2小题则是在运算的过程中需要对a是否大于零进行讨论。
解:(1)当a>0,b>0,则f(x)为单调递增,当a<0,b<0,则单调递减。
(2)f(x+1)-f(x)=a·2x+b·3x>0
当a<0,b>0时,
当a>0,b<0时,
4.根据图形的位置、形状分类整合
图形的位置、形状分类整合是指由几何图形的不确定性而引起的分类讨论,如一次函数、二次函数的图象,幂函数、指数函数的图象,对数函数的图象等,这种方法也适用于几何图形中点、线、面的位置关系的研究以及解析几何中直线与圆锥曲线的位置关系。
5.根据含参数问题的分类讨论
某些含有参数的问题,由于参数的取值不同会导致所得的结果不同,需对参数进行讨论,或者由于对不同的参数值要运用不同的求解或证明方法等。如含参数的方程、不等式、函数等。解决这类问题需要合理确定分类标准,讨论中做到不重不漏,结论整合要周全。
例1.设奇函数f(x)的定义域为R,当x>0时,f(x)= (这里m为正常数)。
若f(x)≤m-2对一切x≤0成立,则m的取值范围为 。
思路剖析:利用函数奇偶性对称性的性质以及基本不等式,可以求出当x<0的函數f(x)的最大值,但是当x=0时必须要分开讨论,否则就遗漏了m的另一部分的范围,故分类讨论一定要周全,不重不漏。
解:当x>0时,当且仅当x=m等号成立,
因为f(x)是奇函数,图形关于原点对称,所以当x<0时,f(x)max=1-2m
又因为当x=0时,f(0)=0
∴
三、简化和避免分类讨论的技巧
分类讨论的思想是一种重要的解题策略,对于培养学生思维的严密性、严谨性和灵活性以及提高学生分析问题和解决问题的能力无疑具有较大的帮助。但它不是万能的。分类讨论思想解题的实质是“化整为零,各个击破,再积零为整”的思维策略,但同时还要注意充分挖掘求解问题中潜在的特殊性和简单性,尽可能消除“讨论因素”,灵活地采用相对应的解题策略,适当作一些“技术处理”,简化或避免分类讨论,往往能给解题带来事半功倍之效,避免分类讨论常见的解题策略有:直接回避、变更主元、整体考虑、反客为主等等。
1.通过逆向思维避免分类讨论
当问题不易直接求解,需要更多的讨论时,可考虑它的反面,通过对其反面情况的分析研究,使问题得到解决。
【例题】在报名的8名男生和5名女生中,选取6人参加志愿者活动,要求男、女生都有,则不同的选取方式的种数为 1688 (结果用数值表示)。
思路剖析:对于排列组合或概率的题目,可以通过分类讨论去解决比较复杂的问题。但是此题若直接做要分5类,反而麻烦,所以考虑它的对立面,用间接法,通过逆向思考就变得简单了。
解:
2.含参数问题可构造函数或分离参数简化分类讨论
3.结合数形结合的思想避免或简化分类讨论
总之,分类讨论是数学中一种重要的思想方法,也是重要的解题策略。由于很多数学问题很难用统一的方法去解决,若将其划分为若干个局部问题,每个局部问题就显得容易解决了,特别是含参数字母的问题,也是近几年来高考重点考查的热点问题之一,需要逐类分别加以讨论,探求出各自的结果,最后归纳出命题的结论,以达到化难为易、化繁为简、解决问题的目的。

