基于力导向算法优化的有向加权网络数据的可视分析

摘  要：复杂关系网络数据的可视分析多采用有向加权的节点-连接图布局。由于节点间的连接关系为多属性数据，传统的布局绘制算法难以完整地呈现数据间的组织结构。本文通过对力导向物理学模型进行优化设计，结合多通道视觉编码设计，完成对复杂关系网络数据可视化的绘制。相比较传统的节点-连接图布局，本算法在呈现多属性网络数据时具有更好的认知效能。

关键词：可视分析;复杂关系网络;力导向布局算法

中图分类号：TN919.8       文献标识码：A 文章编号：2096-4706（2019）19-0088-05

Abstract：Visual analysis of complex relational network data mostly uses directed weighted node-join graph layout. Because the connection relationship between nodes is multi-attribute data，the traditional layout rendering algorithm is difficult to fully present the organizational structure of data. By optimizing the force-directed physical model and combining with the design of multi-channel visual coding，this paper completes the visualization of complex relational network data. Compared with the traditional node-connection graph layout，the algorithm has better cognitive performance in presenting multi-attribute network data.

Keywords：visual analytics;complex relational network;FDLA（Force-Directed Layout Algorithms）

0  引  言

在移动互联网高度发达的今天，关系网络数据是分析群体社交行为、组织结构模式、行业流程规划等课题的重要手段。通过对多属性关联关系进行信息结构建模，同时结合可视化设计和数据挖掘等手段，可以帮助用户快速提取出数据背后隐含的模式信息。

现有的可视化方法多采用节点-连接图布局来绘制关系网络数据，当节点间的连接关系包含多种属性（如起止方向、权重）时，需要采用有向加权图布局进行绘制。现有方法的基本思路是通过FR算法、KK算法等力学模型对关系网络进行建模，求解整个关系网络在力平衡或者能量平衡状态下的分布，来完成图布局的绘制。该方法在于面对大规模节点集合的网络数据时，绘制效能和呈现效果会明显下降;此外，简单的力学模型无法解决连接线之间互相遮挡的问题，难以满足多属性关联关系的绘制需求。

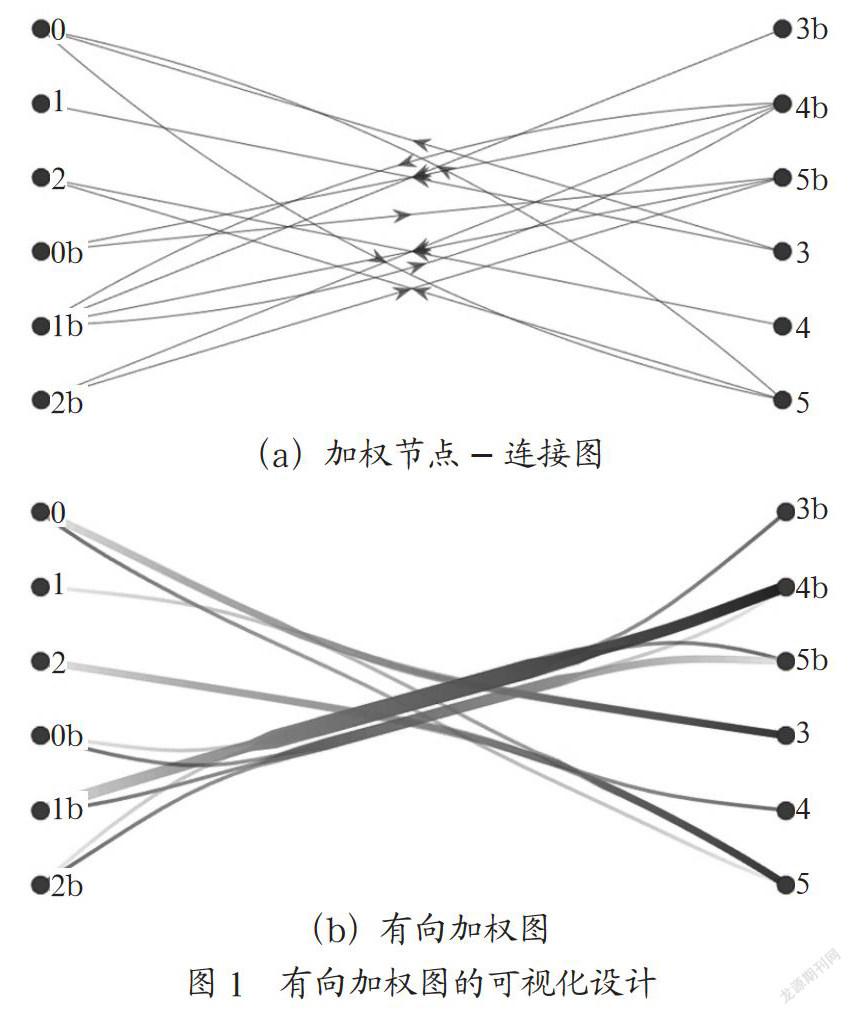
针对高维关系网络数据可视化，本文对有向加权图布局的力学模型进行了优化，以实现更加合理的、方便用户视觉认知的布局效果，如图1所示。

1  基于多属性关系数据的有向加权图

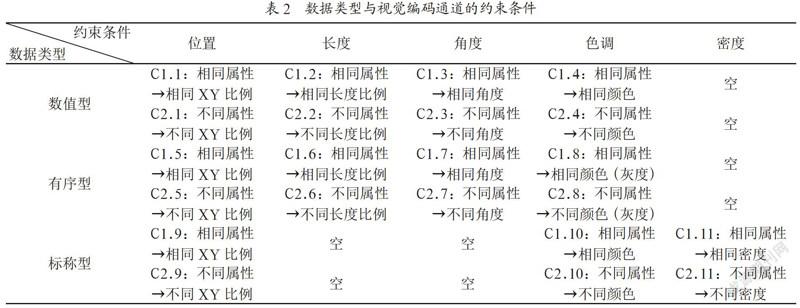
关系网络数据的复杂度主要表现在两方面：节点数量与节点间连接数的相对比例、连接关系包含的属性维度。前者取决于关系网络的规模，对于网络大数据而言，网络规模的量级对节点-连接图布局的绘制效率有直接影响，但对视觉认知有效性的影响并不明显;当节点间关系为多属性数据时，简单的节点-连接图布局难以完整地呈现数据结构信息，需要调动更多的视觉认知通道进行视觉编码，同时协调各编码通道之间的一致性，达到合理的有向加权图绘制效果。以表1所示的全球贸易网络数据为例，在一条交易关系记录中，可能涵盖了进/出口、贸易货物量、交易周期、顺差/逆差、交易价格、征税情况等多种属性，是典型的多属性关系数据。这时，需采用有向加权图的布局形式，综合运用线宽、颜色、渐变、线型、透明度等多种视觉通道对贸易关系中的各项属性进行视觉编码，来完成可视化绘制。

2  有向加权图的力导向算法优化

力導向布局算法的核心思想，是将电场、能量场以及胡克定律等物理概念引入图的布局空间，通过对绘制空间中各节点施加物理场作用，计算整个节点集合在场作用力平衡状态下的分布，进而得到节点的布局结果。

力导向布局算法中较有代表性的如KK算法和FR算法，是将各节点视为在物理场中游离的点（例如原子，或小球），然后对其进行力学模拟（如电场力或者弹簧力）。由于电场中同性相斥的原理，所有的节点之间彼此存在排斥力，使得节点互相远离对方;此外，如果节点之间有连接关系，则节点之间存在吸引力，趋于相互靠近;在此基础上循环模拟力场作用下节点的运动，迭代计算出引力和斥力达到平衡的状态下，各个节点的分布坐标。

在力导向布局模型中，假设有向加权图G=（V，E），节点集合为V，有向边集合为E。节点u，v∈V，则节点u，v之间的排斥力为：

其中，kt为节点u，v之间设置弹簧的自然长度。dist（u，v）为节点u，v之间的当前距离。节点之间的距离越近，则排斥力越强。

此外，如果节点u，v之间存在连接，则存在吸引力为：

其中，K=|D（u）-D（v）|-l，是节点u，v之间的引力调节因子。l为节点u，v之间的平衡距离。节点间距离越大，则相互吸引力越大。

对于集合V中的全部节点，通过算法循环依次计算排斥力Fr与吸引力Fa，驱动节点移动。

对整个节点集合，通过设置位移收敛的条件，使节点的运动逐渐趋于稳定状态，整个有向加权图达到能量均衡状态，其条件定义为：

其中，Eattraction是节点集合V中各节点间的引力场能量值，Eresistance是各节点间斥力场的能量值，αc是集合内的布局距离调节因子，用于调整图布局中节点的疏密程度。

这里，采用模拟退火算法cool（t），来保证物理场模拟的收敛，其模型为：

其中，p（E）指出点集合能量值状态Eg的概率分布，作为温度T和波茨曼常数k的因变量。在温度不断冷却时，整个系统的能量状态越来越低，直至温度为0。

由上述分析可以看出，经过优化的力导向布局算法的逻辑框架为：

（1）数据的预处理;

（2）基于电场力计算节点间的排斥力作用;

（3）基于胡克定律计算关联节点间的引力作用;

（4）迭代计算节点集合的能量值，回归至能量平衡状态。

整个布局绘制的流程如下：

Step1：对多属性关系数据进行聚类预处理（K-means或者SOM方法）;

Step2：计算集合中各个节点与其余所有节点之间的排斥力，以及斥力作用下相互距离;

Step3：计算存在关联的节点之间的吸引力，以及引力作用下的相对距离;

Step4：迭代更新各节点在引力和斥力作用下的位置坐标。引入模拟退火算法，每个节点在本次循环中的坐标能量值逐渐降低。

Step5：循环结束，得到节点集合在均衡状态下的布局。

Step6：绘制节点和连线。

3  视觉增强设计

3.1  基于边权重的线型调整

对于规模较大的关系网络，由于节点数量多，当节点之间坐标相对接近时，密集的连接线可能会产生严重的遮挡，造成用户难以有效地识别数据分布特征。一种改善的方法是将连接边绘制为曲线，通过线条的弯曲拉开空间距离，提高视觉辨识度。

弯曲连接边可能带来的问题是对连接关系的误读。通过对用户的视觉认知经验进行研究发现，当线条表征两个端点间的连接关系时，普通人倾向于沿连线切线的最大概率方向寻找两个端点。也就是说，用户习惯于在视觉上将曲线拟合成近似的直线，然后基于直线的方向延伸在复杂的网络连接中去追踪节点。换句话说，连接线曲率越大，用户对节点之间连接关系视觉认知的准确性就越低。

对于多属性连线图来说，有向边的权重可以作为绘制连线时视觉认知准确性的主要参考因素。本文的方法是在复杂的连接图中，建立边的权重与曲率之间的反向关联，具体方法为：

首先，设置边与边之间的相容性系数Ce，作为控制有向边曲率的变量。在总的相容性系数Ce中增加权重相容性系数Cw，其计算公式为：

Cw（P）=1-Wq/（Wp+Wq）

Cw（Q）=1-Wp/（Wp+Wq）

其中，Wp和Wq分别为边P和边Q的权重值，在本文中以该边的流通量表示。

边P和Q上相应控制点的计算公式为：

通过上述模型可以看出，边的曲率受到相容性系数因子Ce的影响，而引力模型中的权重项Cw与曲率为反向关联。当连接边的权重值越高，则线条的曲率越小，反之则越大。由此绘制的图布局中，权重较高的连接边可以相对接近自身的直线形态，而权重低的边则会出现较明显的弯曲，这样的设计在保证了边之间的辨识度的同时，兼顾了集合中重要数据的视觉认知准确性。

3.2  基于密度评估的透明度算法

除了绘制曲线的连接边以外，还可以通过控制透明度来降低边之间的遮挡干扰。实验表明，当大量连线叠摞在一起时，绘制半透明的线条，可以有效降低相互遮挡的视觉干扰。本文算法基于边密度对透明度进行计算，可实现连线密集区域的半透明效果绘制。

算法的基本思想是首先建立边的相似度函数，通过计算集合中所有连接边的分布密度，将图划分成多个不同密度等级的集合。在每个边集中，根据边的区域位置不同，可归类为中心区域和跨边界区域。建立区域透明度与边密度的关联函数，区域的边密度越大，则该集合中心区域的连接线透明度越高，以有效减少视觉杂乱。

4  有向加权图的视觉编码设计

在数据可视分析设计中，需要依据数据类型及呈现的需求来选择视觉编码的方法。按照常规的数据类型划分，主要分为数值型、标称型和有序型数据3类;视觉编码通道通常划分为：位置、几何参数（长度、角度、面积等）、填充属性（色调、饱和度、密度、纹理等）和形状。视觉编码通道对于不同数据类型的属性表达效果是有所区别的。

针对不同的关系網络数据集合，如何合理地对视觉编码通道进行分配，需要基于认知规律进行分析评估。本文针对多属性的节点-连接图进行了用户研究实验：首先，在三种类型的数据进行视觉映射的排位优先级中，选择排序相对靠前的通道（表明该通道基本适用于各种数据类型），对于多属性的节点-连接图来说，连接关系是以直线（或者曲线）表示，本文选择了其中较为主要的5种编码通道，分别是：连线的宽度、长度、填充颜色、线型和透明度等属性，作为一致性约束分析的元素。基于一致性约束的模型，对数据属性和映射方式进行分解，组合得到二十多种不同的情境，如表2所示。

针对每种具体的情境，分别按照符合一致性约束的原则和打破一致性约束的原则进行多视图绘制，并由用户进行绘制效果的合理性评估。第一种情况称为“自发约束”，即用户基于视觉认知自发地选择了符合C1和C2的一致性约束条件;另一种情况下，为了确认“非一致性约束”条件存在的合理性，当用户的评估认为多视图绘制打破一致性约束条件更有利于视觉认知时，实验会要求用户进行二次确认，是否存在一种用户认为可能绘制效果更好的视觉映射和编码的方式。此时存在两种可能：“提醒约束”和“例外”。“提醒约束”指虽然用户的自发选择打破了一致性约束的条件，但经系统提示后，用户选择了遵循原有的一致性约束条件;“例外”指受试者在系统提示的情况下，依然选择打破一致性约束原则，并认为这样更符合人的认知规律。基于上述方法完成测试并对结果进行统计分析，以得到符合用户视觉认知规律的一致性约束模型作用条件。

可以看出：

（1）C1的確认与“例外”比C2更频繁，这是因为C2一般可以自动得到遵守;

（2）关于XY比例尺的确认与“例外”比颜色比例尺更频繁，可能是因为实验中使用位置编码比使用颜色编码更频繁;

（3）所有经过提醒的确认都属于C1，其中约一半是关于编码测量名称的标称型比例尺，且没有关于测量名称的例外，说明受试者倾向于认为测量名称的一致性重要，但有时会忽视这一点。

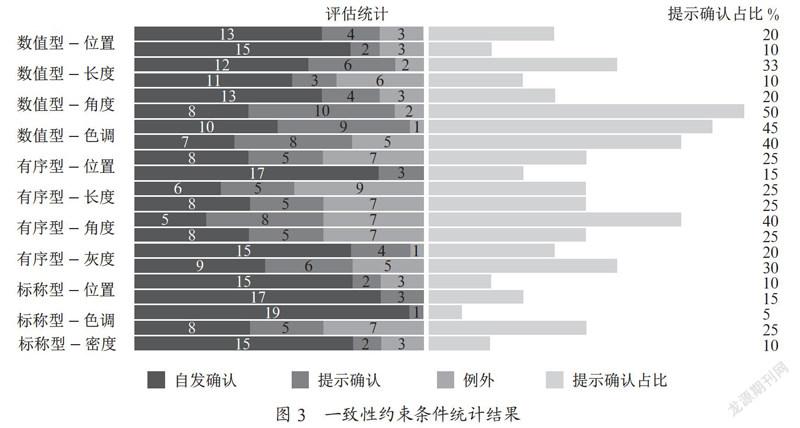
全局的统计结果如图3所示。

从全局的统计结果来看：

（1）一些约束没有出现“例外”：C2.1，C2.2，C1.3，C1.4;

（2）一些约束出现比较高比例的“例外”：C1.1，C2.3，表明一致性约束需要综合考虑是否进行比较，是否造成过多的空白区域和色度的语义;

（3）此外，实验中还发现，对于属性是否相同，需要更微妙的定义。一些受试者会采用一些其他的策略，如：坐标轴拥有相同的值标签，趋势线的一致性等;

（4）对于数值型和有序型数据而言，角度和色调通道都是提示确认情况发生概率较高的区域，用户的认知习惯在这方面表现较为分散，在使用时需要慎重。

因此，通过测试可以做出以下分析：

（1）对不同的约束，确定它们适用的范围，再确定何时系统需要执行约束条件;

（2）允许约束模型个性化，能够学习用户习惯并确定适合用户的约束模型;

（3）给出修改后的预览图，用户可以快速预览效果并做出选择;

（4）绘制视图时应清楚地向用户传达不一致之处和可能的影响。

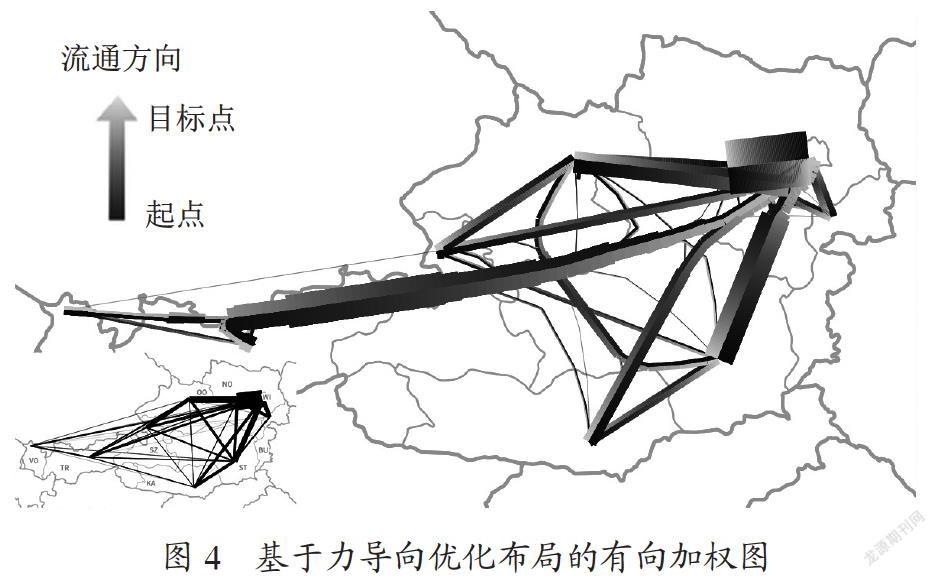
基于上述研究，最终完成有向加权图的绘制如图4所示（左下角为无向加权图模式）。

5  结  论

本文研究针对有向加权图的数据结构特点，将连接边的方向、权重值等属性作为视觉编码的要素，纳入力导向模型布局计算，在完整可视化复杂关系数据的各项属性的同时，通过线型调控、基于边密度绘制透明度等方法进一步降低了复杂图的视觉杂乱和干扰问题。同时，对于如何提升大规模关系数据的视觉辨识度，在后续工作中还需要进一步研究。

参考文献：

[1] 蔡朱华.基于聚类分析的可视化技术及其应用研究 [D].厦门：厦门大学，2014.

[2] 陈海东.不确定性可视化及分析方法研究 [D].杭州：浙江大学，2015.

[3] 丁治宇，陈海东，吴斐然，等.多变量空间数据场可视化综述 [J].计算机辅助设计与图形学学报，2013，25（11）：1597-1605.

[4] 姜晓睿，郑春益，蒋莉，等.大规模出租车起止点数据可视分析 [J].计算机辅助设计与图形学学报，2015，27（10）：1907-1917.

[5] 韦岗，曹燕，王一歌，等.计算机音乐可视化表征谱设计 [J].现代信息科技，2019，3（14）：5-7.

[6] 李春好，田波，刘玉国.逆层次分析法——复杂经济社会系统评价问题的新方法探索 [J].吉林大学社会科学学报，2007（3）：118-124.

[7] 刘芳，田凯，周志光，等.基于SOM和引力场聚类的金融数据可视化 [J].计算机辅助设计与图形学学报，2012，24（4）：435-442.

[8] 汤晓燕，刘文军，朱东，等.基于ECharts的电动汽车监控可视化研究 [J].现代信息科技，2018，2（12）：46-48.

[9] TELEA A，ERSOY O，HOOGENDORP H，et al. Comparison of Node-Link and Hierarchical Edge Bundling Layouts：A User Study [C/OL]//Dagstuhl Seminar Proceedings 09211：Visualization and Monitoring of Network Traffic.[2009].http：//drops.dagstuhl.de/opus/volltexte/2009/2154.

[10] BATTISTA G D ，EADES P ，TAMASSIA R ，et al. Graph drawing：Algorithms for the visualization of graphs [M]. Prentice Hall PTR Upper Saddle River，NJ，USA，1998：258-264.

[11] CHANG B. Ecological footprint analysis based on RS and GIS in arid land [J].Journal of Geographical Sciences，2005，15（1）：44-52.

[12] CARPENDALE S.Evaluating information visualizations [M]//Lecture Notes in Computer Science.Heidelberg：Springer-Verlag，2008，4950：19-45.

[13] HURTER C，ERSOY O，TELEA A. Graph Bundling by Kernel Density Estimation [J]. Computer Graphics Forum，2012，31（3pt1）：865-874.

[14] COX D ，HARRIS R G . North American Free Trade and Its Implications for Canada：Results from a CGE Model of North American Trade[J]. World Economy，1992，15（1）：31-44.

[15] HOLTEN D . Hierarchical Edge Bundles：Visualization of Adjacency Relations in Hierarchical Data [J]. IEEE TRANSACTIONS ON VISUALIZATION AND COMPUTER GRAPHICS，2006，12（5）：741-748.

[16] DANNY Holten，JARKE J. van Wijk. Force-Directed Edge Bundling for Graph Visualization [J]. Computer Graphics Forum，2009，28（3）：983-990.

[17] GANSNER E R，HU Y，NORTH S，et al. Multilevel Agglomerative Edge Bundling for Visualizing Large Graphs [C]// Pacific Visualization Symposium （PacificVis）. IEEE Xplore，2011，18（1）：187-194.

[18] FRANK S，KAUFMAN A. Out-of-Core and Dynamic Programming for Data Distribution on a Volume Visualization Cluster [J].Computer Graphics Forum，2009，28（1）：141-153.

[19] FRUCHTERMAN T M J，REINGOLD E M. Graph drawing by force-directed placement [J].Software-Practice and Experience，1991，21（11）：1129-1164.

[20] YING-HUEY F，WARD MO，RUNDENSTEINER EA.Hierarchical parallel coordinates for exploration of large datasets [C].//Proceedings of visualization '99.Los Alamitos，IEEE Computer Society Press，1999：43-50.

[21] GRUENDL H ，RIEHMANN P ，PAUSCH Y ，et al. Time-Series Plots Integrated in Parallel-Coordinates Displays [J]. Computer Graphics Forum，2016，35（3）：321-330.

作者简介：巫滨（1978-），男，漢族，江苏常州人，博士，讲师，研究方向：大数据可视化分析、真实感计算机图形学及虚拟现实环境设计。