一种双面型宽频带的左手材料设计研究

代小琴 迟洁茹 何光峰 宋来军

摘要：  针对目前左手材料普遍存在的谐振频率低、带宽窄和高损耗的问题，本文基于谐振型左手材料理论，设计了一种双面型宽频带左手材料结构。该结构将螺旋对称形金属片与十字形金属片分别放置在介质基板的两侧，形成一个左手材料单元，在2个左手材料单元顺序排列条件下，实现最佳谐振性，为了验证所设计的材料结构是否具有左手特性，采用高频仿真软件进行电磁仿真，同时采用Matlab软件与传输反射法（nicolsonrossweir，NRW）进行计算。研究结果表明，该材料在3.37～5.87 GHz范围内，具有谐振特性，满足低损耗要求;在2.5～4.8 GHz范围内，介电常数和磁导率同时为负，实现了材料的左手特性。该研究具有一定的实际应用价值。

关键词：  双面型; 宽频带; 左手材料; 左手特性

中图分类号： TB303 文献标识码： A

左手材料（lefthanded metamaterials，LHM）[1]这一理论概念，最早是由前苏联物理学家V.G.Veselago[2]提出。在左手材料中，电场矢量、磁场矢量和波矢量三者遵循左手规则，不同于以往人们习惯的右手定则，电磁特性参数等效介电常数ε和等效磁导率μ均为负数。电磁波在左手材料中传播时，其相速度和群速度的方向相反，并具有负折射、反多普勒效应、负切伦科夫效应和完美透镜效应[3]等一系列不常研究的物理现象。由于在大自然中不存在这种物质，使这一理论没能得到更深入的研究。直到30年后，英国物理学家J.B.Pendy等人[4]设计了细金属棒和谐振环结合的材料模型，这种周期排列的人工介质，通过实验测试，证明它是一种在微波段同时具有负介电常数与负磁导率的特异性材料，即开口谐振环结构，随之科学界纷纷投入对左手材料的研究，并成为研究热点，因此，不同新型的具有左手特性的材料結构，如Smith经典结构[5]、S形结构[6]、十字环形结构[7]、对称环结构[8]及H形结构[9]等被相继提出，但这些研究都存在着结构复杂、频宽窄、损耗大和体积大等一系列问题，在某种程度上阻碍了左手材料的发展应用。基于此，本文设计了一种双面型宽频带左手材料结构，该结构是在螺旋对称环结构模型[10]的基础上，对结构进行重新设计、优化尺寸，使其在中低频段上具有较高的带宽，并通过高频仿真软件（high frequency structure simulator，HFSS）13进行电磁仿真和优化，得到S参数幅度曲线，并通过Matlab R2015b软件编程，对S参数提取出相关的等效电磁参数[1113]。仿真结果表明，该结构具有2.5 GHz的频带带宽，并在2.5～4.8 GHz的频段上具有负的等效介电常数和负的等效磁导率，相对带宽可达54.11%，证明了该材料结构单元设计的正确性与合理性。该设计结构简单、宽频带、低损耗，应用前景广阔。

1 设计原理

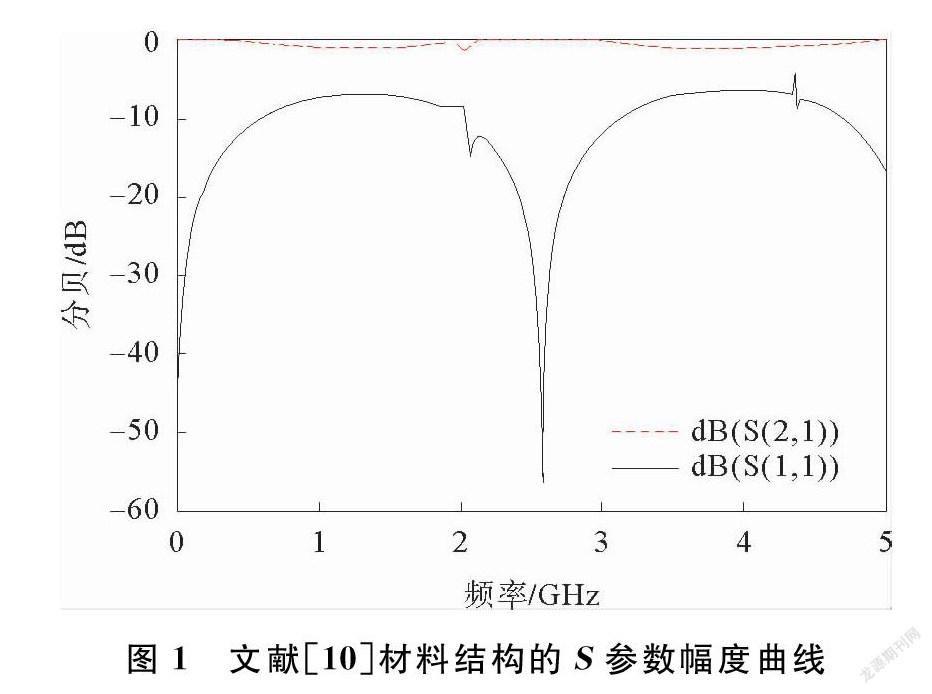
左手材料是由材料结构单元在空间中规则排列构成。由于左手材料单元在空间中的排列方式和分布情况不同，左手材料所表现出来的性质各异，如果一个左手材料的单元结构尺寸远小于电磁波在空间中的波长λ时，该种左手材料即可被认为是均匀的介质[14]，所有左手材料的电磁特性都可以用它存在的、宏观的等效电磁参数介电常数、磁导率和折射率来定义。文献[10]设计了单面型螺旋对称环结构的左手材料，文献[10]材料结构的S参数幅度曲线如图1所示。由图1可以看出，谐振频率范围在2.03～3.15 GHz之间，谐振频率低，谐振频带太窄，而在实际应用时，往往需要较宽的频带。

在电磁场作用下，介质基板两侧的金属短线将会等效成LC谐振电路，整个结构在谐振频率附近实现负的介电常数和负的磁导率[15]。本文在介质板背面加载十字金属片，当电磁波平行入射时，电场方向的金属线产生电谐振，而磁场平行于介质板平面，两侧金属结构上产生回型电流，形成电感，两侧金属片相对应的边缘位置出现异种电荷，具有感应电容的效应，整个材料结构组成一个完整的LC谐振电路，谐振频率f与LC谐振电容C及电感L之间满足等式

由电磁谐振型理论分析可知，本设计实现了在介质基板两侧集成电谐振器和磁谐振器，在一定频率下具有左手特性[16]。

2 结构设计

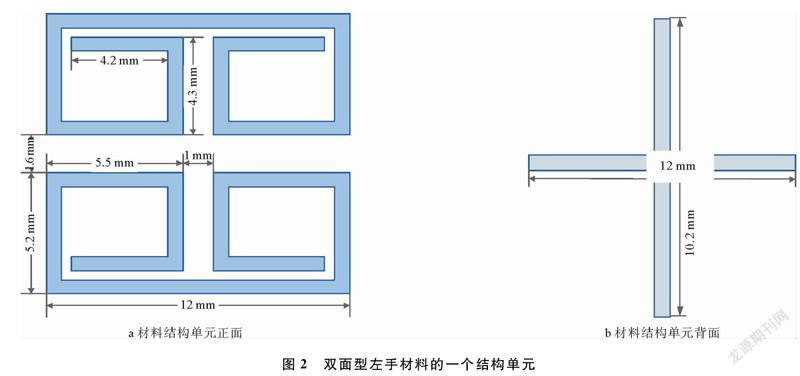
本文对双面型左手材料进行结构设计，双面型左手材料的一个结构单元如图2所示。FR4基质介电常数为4.4，其中所有金属线宽为0.6 mm，介质基板长为13 mm，宽为14 mm，厚度为m=0.25 mm，正面谐振螺旋环长为12 mm，环宽为5.2 mm，上、下两环间的距离为1.6 mm，内环长为4.2 mm，高度为4.3 mm，小环间的距离即左右距离为1 mm，谐振环距上下边缘的距离均为1 mm，距左右边缘的距离均为0.5 mm。介质板背面的十字金属片，横向金属片的长度为12 mm，竖向金属片的长度为10.2 mm。波导壁由两对对称的理想电壁和理想磁壁组成，上、下两电壁的间距为14 mm，前、后两磁壁的间距为16.45 mm。

3 仿真验证与参数分析

为验证所设计的材料结构是否具有左手特性，本文采用高频仿真软件HFSS 13.0进行电磁仿真，材料结构仿真模型如图3所示。沿x正方向的左、右端口设置2个波端口激励，为Wave Port，归一化阻抗设置为377 Ω，即空气的特性阻抗[17]，求解频率设置为10 GHz，选择快速扫描方式，频率区间从0～8 GHz。本设计是两个材料单元顺序排列构成一个整体模型，单元间的距离为1 mm。

该模型能够模拟平面电磁波[18]从左端口经材料介质，传播到右端口的反射和透射特性，得二端口波导的反射系数S11和透射系数S21，S参数幅度值随频率变化曲线如图4所示。由图4可以看出，在3.37～5.87 GHz频段形成通带范围，-10 dB带宽为2.5 GHz，且在谐振通带内，S21的幅度接近零，说明材料结构单元的传输损耗相对较小，进而满足低损耗的要求。

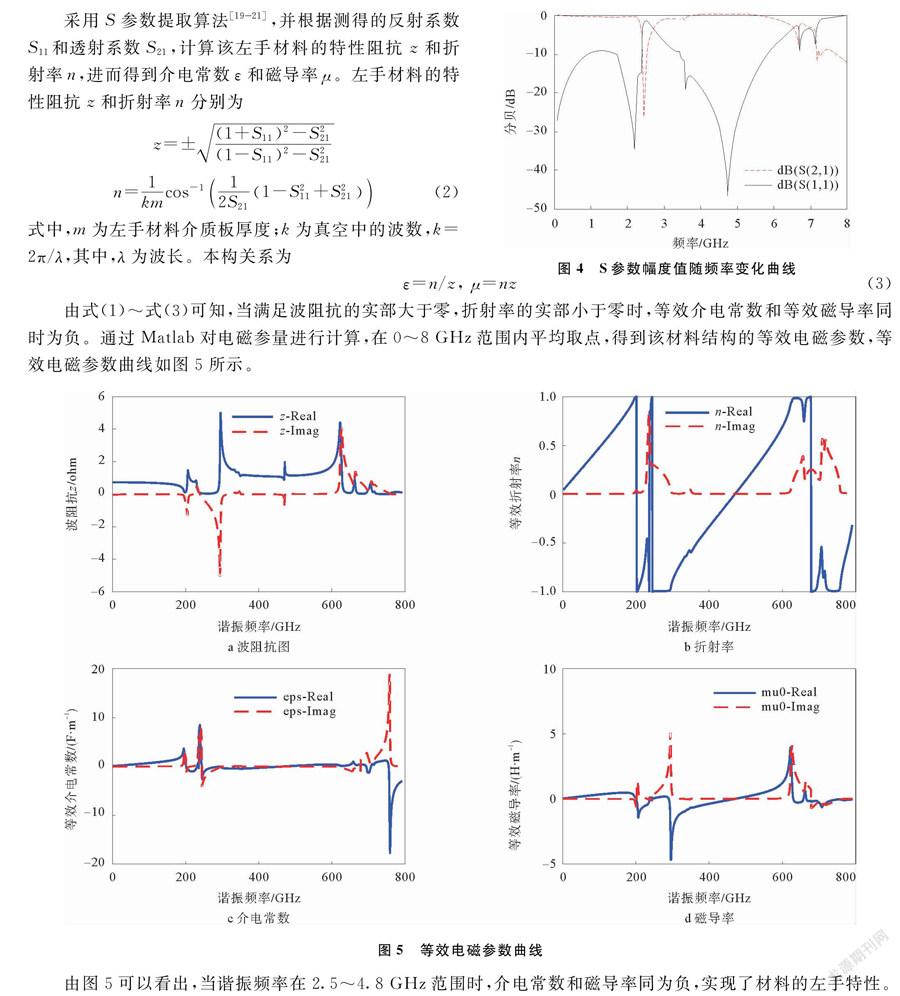
由式（1）～式（3）可知，当满足波阻抗的实部大于零，折射率的实部小于零时，等效介电常数和等效磁导率同时为负。通过Matlab对电磁参量进行计算，在0～8 GHz范围内平均取点，得到该材料结构的等效电磁参数，等效电磁参数曲线如图5所示。

由图5可以看出，当谐振频率在2.5～4.8 GHz范围时，介电常数和磁导率同为负，实现了材料的左手特性。

4 结束语

本文对传统的单面型螺旋对称环结构进行了改进，设计了一种新型的材料结构，在介质基板背面加载十字形金属片，形成一个新的材料单元。在2个左手材料单元顺序排列的情况下，对材料结构进行理论分析，并采用HFSS软件进行电磁仿真，同时采用Matlab软件与NRW反演算法进行计算。研究结果表明，该结构在3.37～5.87 GHz具有谐振特性，传输损耗小，其-10 dB带宽可达2.5 GHz，在2.5～4.8 GHz范围具有双负特性。该设计实现了在5 GHz左右非常好的谐振性，2.3 GHz的绝对左手特性带宽。该设计形状简单，易于实现，具有广泛的应用领域。

参考文献：

[1] 王小军， 文庆珍， 朱金华. 左手材料的研究进展[J]. 材料开发与应用， 2011， 26（2）： 6874.

[2] Veselago V G. The elect rodynamics of substances with simultaneously genative values of permittivity and permeability[J]. Sov Phys Usp， 1968， 10（4）： 509514.

[3] 马中团， 鲁拥华， 王沛， 等. 左手性材料研究进展[J]. 物理， 2004， 33（7）： 497502.

[4] Pendry J B， Hoiden A J， Stewart W J， et al. Youngs extremely low frequency plasms in metallic macrostructures[J]. Phys Rev Lett， 1996， 76： 47734776.

[5] Smith D R， Padilla W J， Vier D C， et al. Composite medium with simultaneously negative permeability and permittivity[J]. Phys Rev Lett， 2000， 84（18）： 41844187.

[6] Ran L， Huangfu J T， Chen Y H， et al. Microwave solidstate lefthanded material with a broad bandwidth and an ultralow loss[J]. Physical Review. B， Condensed Matter， 2004， 70（7）： 715.

[7] 楊晨， 张洪欣， 王海侠， 等. 十字环形左手材料单元结构设计与仿真[J]. 物理学报， 2012， 61（16）： 164101（19）.

[8] 杜国宏， 刘昆. 用于左手材料的对称开口谐振环特性研究[J]. 四川大学： 自然科学版， 2010（5）： 10531058.

[9] 刘亚红， 罗春荣， 赵晓鹏. 同时实现介电常数和磁导率为负的H型结构单元左手材料[J]. 物理学报， 2007（10）： 58835889.

[10] 徐瑞迪. 基于对称环结构的左手材料单元设计及其在多频天线中的应用研究[D]. 厦门： 厦门大学， 2015.

[11] Smith D R， Veir D C， Koschny T， et al. Electromagnetic parameter retrieval from inhomogeneous metamaterials[J]. Physical Review E， 2005， 71（3）： 14.

[12] 吴俊芳， 孙明昭， 张淳民. 左手材料的响应频段和单元尺寸关系的研究[J]. 物理学报， 2009， 58（6）： 38443847.

[13] 李芷懿. 非对称人工结构等效电磁参数提取[D]. 西安： 西安电子科技大学， 2015.

[14] Smith D R， Padilla W J， Vier D C， et al. Composite medium with simultaneously negative permeability and permittivity[J]. Phys Rev Lett， 2000， 84（18）： 41844187.

[15] 张效雄， 王佳云， 杨荣草. 基于十字线与双开口环结构的双频段左手材料[J]. 测试技术学报， 2017， 5（31）： 455460.

[16] 孔娟. SIAD结构左手特性的研究与应用[D]. 南京： 南京理工大学， 2010.

[17] 杜雷鸣， 谢彦召， 王绍飞. 平行板传输线特性阻抗仿真计算及解析修正[J]. 强激光与粒束， 2015， 27（8）： 154158.

[18] 雷前召， 阴国富. 多层介质中平面电磁波传播特征[J]. 河南师范大学学报， 2012， 40（2）： 14.

[19] 丁敏， 薛晖， 吴博， 等. 基于电磁超材料的两种等效参数提取算法的比较分析[J]. 物理学报， 2013， 62（4）： 044218（16）.

[20] 杨光， 姜山， 王国栋. 一种改进的电磁参数测试算法[J]. 国外电子测量技术， 2007（8）： 1517.

[21] 田步宁， 杨德顺， 唐家明. 传输/反射法测量材料电磁参数的研究[J]. 电波科学学报， 2001（1）： 5760.