基于Matlab图形用户界面的投资组合优化系统研究

王超 杨德平

摘要：  针对马科维兹均值方差模型建模求解过程较复杂的问题，本文以均值方差模型为主要理论依据，借助Matlab软件中GUI工具开发投资组合优化系统。该系统主要实现了数据的读取与筛选、均值方差有效前沿及不同策略投资组合均值方差的计算功能，并引入投资策略选择选项与自定义资产权重功能，提高了该系统的灵活性与易用性，最后选取2018年1月～3月浦发银行、宝钢股份、上汽集团3只股票数据对该系统进行分析测试。测试结果表明，投资组合优化系统界面友好，操作简单，解决了有效前沿建模计算繁琐的问题，可用于大规模数据的筛选与计算。该研究优化了投资决策过程，提高了投资策略在投资组合构建过程中的利用度，具有一定的实际应用价值。

关键词：  图形用户界面; 均值方差模型; 组合优化; 风险平价

中图分类号： F830.591; TP317.4 文献标识码： A

证券及其它风险资产的投资首先需要解决预期收益与风险两个核心问题。投资者通常厌恶风险而偏好收益，对于相同的风险水平，会选择投资收益率最大的组合;对于预期收益率相同的投资，会选择风险最小的组合。因此，如何测定投资组合的风险与收益及如何平衡二者进行资产分配是急需解决的问题。投资组合有诸多理论模型和配置方法，如均值方差模型、BlackLitterman模型、等权重方法、美林投资时钟理论等。H.M.Markowitz[1]最早系统地构建了均值方差模型，并将该模型的输入参数设定为风险资产的预期收益、收益标准差以及资产的相关性;R.C.Merton[2]指出了均值方差模型的两大问题，一是最优解使个别资产占据了绝大多数的资金，二是均值方差模型的结果会由于期望收益的较小变化发生显著变化。对此，Michaud[3]提出了投资组合重新取样法，一定程度上缓解了输入参数敏感的问题，但仍无法完全解决均值方差模型的局限性;F.Black[4]提出了基于均值方差模型和贝叶斯理论的BlackLitterman模型，该模型克服了均值方差模型的局限性，将历史均衡收益与先验观点结合起来;Benartzi等人[57]对等权重法进行研究，发现等权重法比均值方差模型法更为稳健。为了改进等权重法风险过度集中的问题，R.N.Sullivan等人[89]采用波动率的倒数作为资产的权重，实现了不同资产贡献的波动率相等;S.Maillard等人[10]详细阐述了由风险平价方法构成的投资组合;E.J.Elton等人[1112]认为风险平价投资组合具有稳健性，因为它与均值方差投资组合优化中的平均相关系数投资组合密切相关;D.B.Chaves等人[1314]对多种方法进行比较，认为风险平价方法在夏普比率方面表现良好，且节约换手费用，但是却高度依赖于选择集。以上研究涉及数据过多，导致建模求解过程非常复杂，因此开发一款界面优好且操作简单的投资组合优化系统非常必要。近年来，图形用户界面（graphical user interface，GUI）引起许多学者的重视，刘芳等人[15]运用GUI构建了电力电子电路仿真平台;孙祥等人[16]运用GUI设计开发系统研究了信号及图像处理。然而也有一些學者将Matlab GUI设计开发系统应用于经济领域，年兴等人[17]研究了基于支持向量机（support vector machine，SVM）的股指预测模型与GUI仿真;黄冉等人[18]运用Matlab GUI开发出灰色预期系统。基于此，本文以组合优化模型为理论依据，运用Matlab GUI开发出投资组合优化系统。该系统主要实现数据的读取与筛选、均值方差有效前沿计算及不同策略投资组合均值方差计算，并选取2018年1月～3月浦发银行、宝钢股份、上汽集团3只股票数据进行了实例分析。该研究解决了有效前沿建模计算繁琐的问题，可用于大规模数据的筛选与计算。

1 概念及理论模型界定

2 投资组合优化系统的设计过程

投资组合优化系统主要包括界面设计、控件属性设计及回调函数编写[20]。本文给出投资组合优化系统界面的设计过程、程序代码及minimunvariance、Risk Parity这2种组合策略的设计代码。

2.1 投资组合优化系统界面建立

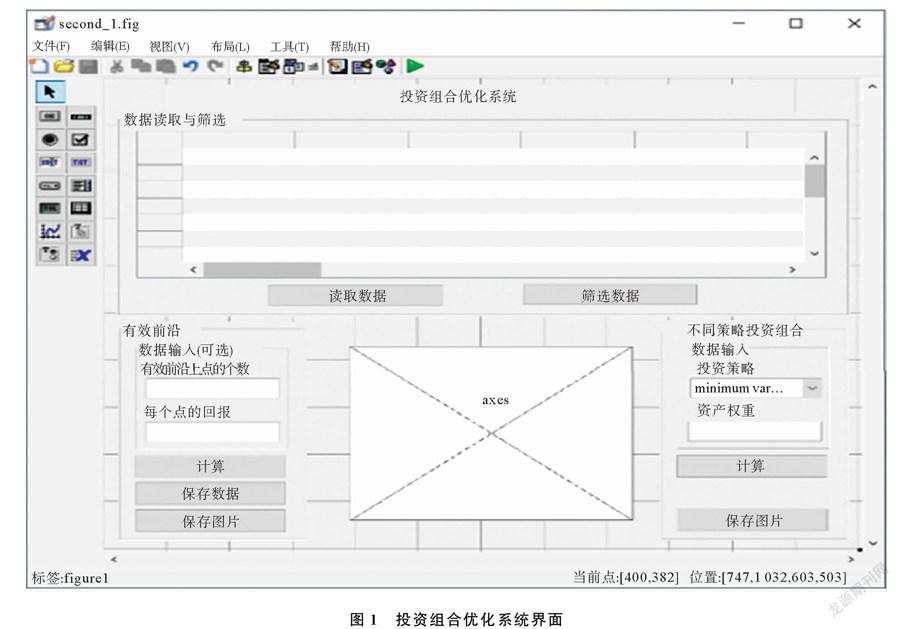
采用Matlab GUI进行系统界面设计，实现数据读取与筛选、均值方差有效前沿计算与绘图以及不同策略投资组合均值方差计算与绘图功能。读取的原始数据及筛选后的数据通过上方表格显示，有效前沿计算结果与不同策略投资组合的均值方差计算结果通过在坐标轴控件中绘图表示。投资组合优化系统界面包含5个静态文本框，3个可编辑文本框，1个弹出式菜单，7个触控按钮，5个面板，1个表格和1个坐标轴控件组成。投资组合优化系统界面如图1所示。

2.2 控件属性及实现功能与程序设计

投资组合优化系统具体控件的主要属性如表1所示。投资组合优化系统主要实现了3个功能：数据读取与筛选功能;均值方差有效前沿计算与绘图功能;不同策略投资组合均值方差计算与绘图功能，其中包含最小方差策略、风险平价策略、1/N策略、随机分配权重、随机产生1 000组权重及自定义权重6种模式。

2.2.1 数据读取与筛选

系统的数据读取采用文件读取方式，点击读取数据按钮，选择相应的excel文件即可读取原始数据，对资产数量与数据样本点个数没有限制。由于数据基数过大，不可避免的会出现时间不一致或数据缺失等问题，因此该系统添加了数据筛选功能，点击筛选数据按钮，即可对原始数据进行筛选，去除日期错误及内容缺失的数据，保持数据在日期上的一致性。具体实现代码如下：

2.2.3 不同策略投资组合均值方差计算与绘图

不同策略投资组合均值方差计算与绘图功能通过弹出式菜单实现。弹出式菜单中包含最小方差策略、风险平价策略、1/N策略、随机分配权重、随机产生1 000组权重以及自定义权重6种模式。用户根据需求自主选择策略，然后点击计算按钮，即可根据筛选后的数据计算出此项策略组合的均值与方差，并在界面中央坐标轴控件中绘图显示。其中，最小方差策略用绿点表示，1/N策略用黄点表示，风险平价策略用黑点表示，随机权重用青点表示，随机1 000组权重用红点表示，自定义用粉色点表示。具体代码如下：

3 系统运行及实例分析

采用2018年1月～3月浦发银行、宝钢股份、上汽集团3只股票数据对该系统进行测试。3只股票部分原始数据如表2所示，其中，第4行上汽集团与最后1行宝钢股份的日期是错误数据，以此来测试该系统数据筛选功能。按此格式将原始数据存入excel表格，该系统即可直接从excel文件读取数据。

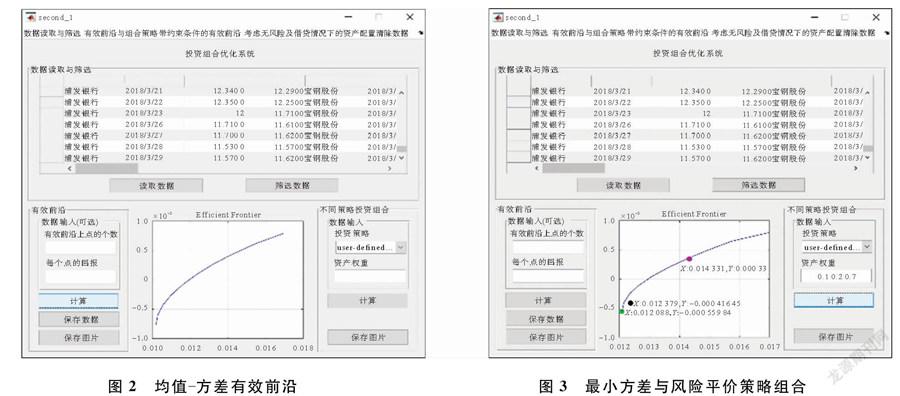
运行该系统，依次点击数据读取按钮与数据筛选按钮进行数据筛选。均值方差有效前沿如图2所示，最小方差与风险平价策略组合如图3所示。

在有效前沿界面中，输入有效前沿上点的个数（可选）及每个点的回报（可选），点击计算按钮，计算浦发银行、宝钢股份、上汽集团3只股票做投资组合的有效前沿，并在坐标轴控件中直接绘图。在不同策略投资组合面板中，选择不同的投资策略，点击计算按钮，得到所构建的投资组合中不同資产的权重及均值与方差，并在坐标轴控件中直接绘图。该系统可将多次计算结果叠加到1张图片中，清晰地表现出不同策略投资组合的收益与风险。本文选取minimumvariance最小方差策略、Risk Parity风险平价策略以及自定义权重（0.1 0.2 0.3）对该系统进行测试。

图2的直角坐标系中，横轴为标准差，表示风险;纵轴为均值，表示收益;蓝线为均值方差有效前沿。在图3的坐标轴控件中，显示的是3次计算叠加图。蓝线为均值方差有效前沿，绿点为以最小方差策略构建投资组合，组合均值为-0.000 559 64，标准差为0.012 088;黑点为以风险平价策略构建投资组合，组合均值为-0.000 416，标准差为0.012 379;粉点是以0.1 0.2 0.7为权重构建的投资组合，组合均值为0.000 33，标准差为0.014 331。由图3可以清晰地比较3种策略的风险与收益，观察到风险平价组合位于可行域内，最小方差组合位于可行域边界上风险最小的位置，自定义权重组合位于均值方差有效前沿上，计算结果准确，系统运行良好。

4 结束语

本文基于Matlab在数值计算、图形绘制及可视化界面开发等方面的优势，以均值方差模型为理论基础，开发了基于Matlab GUI的投资组合优化系统。该系统实现了数据读取与筛选、均值方差有效前沿计算绘图及不同策略投资组合均值方差计算的3大功能，但未设计添加报错功能，对输入变量错误导致的系统错误无法及时报错。该系统解决了有效前沿建模计算繁琐的问题，实现了风险平价模型的求解。该投资组合优化系统界面友好简单易操作，优化了投资决策过程，提高了投资策略在投资组合构建过程中的利用度。目前该系统所涉及的投资策略模型有限，大量策略模型尚未涉及，因此需要进一步编写相应代码进行研究，并对界面进行再设计。

参考文献：

[1] Markowitz H M. Portfolio selection[J]. The Journal of Finance， 1952， 7（1）： 7791.

[2] Merton R C. On estimating the expected return on the market： an exploratory investigation[J]. Journal of Financial Economics， 1980， 8（4）： 323361.

[3] Michaud R O. The markowitz optimization enigma： is 'optimized' optimal？[J]. Financial Analysts Journal， 1989， 45（1）： 3142.

[4] Black F， Litterman R B. Asset allocation： combining investor views with market equilibrium[J]. The Journal of Fixed Income， 1991， 1（2）： 718.

[5] Benartzi S， Thaler R H. Naive diversification strategies in defined contribution saving plans[J]. American Economic Review， 2001， 91（1）： 7998.

[6] Windcliff H，  Boyle P P. The 1/n pension investment puzzle[J]. North American Actuarial Journal， 2004， 8（3）： 3245.

[7] Demiguel V， Garlappi L， Uppal R. Optimal versus naive diversification： how inefficient is the 1/N portfolio strategy？[J]. Review of Financial Studies， 2009， 22（5）： 19151953.

[8] Sullivan R N. Speculative leverage： a false cure for pension woes： author response[J]. Financial Analysts Journal， 2010， 66（4）： 14， 16.

[9] Asness C S， Frazzini A， Pedersen L H. Leverage aversion and risk parity[J]. Social Science Electronic Publishing， 2012， 68（1）： 4759.

[10] Maillard S， Roncalli T， Teiletche J. On the properties of equallyweighted risk contributions portfolios[J]. Journal of Portfolio Management， 2010， 36（4）： 6070.

[11] Elton E J， Gruber M J. Modern portfolio theory， 1950 to date[J]. Journal Banking & Finance， 1997， 21（11/12）： 17431759.

[12] Andreas S. Risk parity for the masses＼[J＼]. Social Science Electronic Publishing， 2011：129139.

[13] Chaves D， Hsu J， Li F F， et al. Risk parity portfolio vs. Other asset allocation heuristic portfolios[J]. The Journal of Investing， 2010， 20（1）： 111.

[14] Anderson R M， Bianchi S W， Goldberg L R. Will my risk parity strategy outperform？[J]. Financial Analysts Journal， 2012， 68（6）： 7593.

[15] 劉芳， 吴成就， 潘俊涛. 基于Matlab/GUI的电力电子电路仿真平台构建[J]. 实验技术与管理， 2016， 33（1）： 107110.

[16] 孙祥， 黄晓鸣. 基于MATLAB的集成化图像处理系统[J]. 科学技术与工程， 2007， 7（20）： 53865388.

[17] 年兴， 朱雨婷， 林剑辉. 基于SVM的股指预测模型与GUI仿真[J]. 消费导刊， 2012（10）： 610.

[18] 黄冉， 杨本硕. 基于Matlab/GUI灰色预期系统开发及应用[J]. 青岛大学学报： 工程技术版， 2014， 29（3）： 3237.

[19] 鲍奕奕. 风险预算管理方法及其应用研究[D]. 上海： 上海交通大学， 2007.

[20] 杨德平， 刘喜华. 经济预测方法及Matlab实现[M]. 北京： 机械工业出版社， 2012.